基于流固耦合的共轴双旋翼气动性分析

翁佳文，邵伟平，郝永平，徐九龙

(1.沈阳理工大学 机械工程学院，沈阳 110159； 2.辽宁省先进制造技术与装备重点实验室，沈阳 110159)

近年来，小型多旋翼无人机凭借其高机动性、垂直起降和悬停飞行的特点，在高效农业植保、地质资源勘探、电力巡检和遥感测绘等诸多方面均有广泛应用[1-2]。为满足环境和功能的要求，已设计出不同种类的无人机，共轴双旋翼无人机因其出色的悬停效率和紧凑的机体结构，在国内外军事和民事领域展现出巨大的应用价值。随着无人机向高速化、灵敏化发展，对无人机的旋翼性能要求也越来越高，对旋翼气动力性能进行准确可靠的预报与检测具有重要的意义。

共轴双旋翼流场特性研究应用的理论主要包括涡输运模型、自由尾迹模型、叶素-动量理论、计算流体动力学(Computational Fluid Dynamics，CFD)等[3]，其中CFD方法可直观展示流场结构特征，随着计算机技术水平的提升，CFD技术逐渐走向成熟[4]，通过不断改进计算方法和网格划分方法，其在不同领域的仿真模拟更具真实性和可靠性。

运用CFD方法对双旋翼进行仿真分析已有很多成果，招启军等[5]通过运动嵌套网格技术与可压RANS方程构建出一种共轴刚性双旋翼悬停流场，着重分析了后掠角、后掠起始位置及尖削非线性弦长分布变化等对共轴刚性旋翼悬停特性的影响。雷瑶等[6]首先通过低速风洞模拟试验得到共轴双旋翼的拉力及功率，再将其运用到CFD仿真模型中，采用滑移网格方法分析了共轴双旋翼在有来流状况下的风扰性能及流场内部的变化规律。Passe B J等[7]应用CFD方法建立了小型双旋翼无人机的自由尾迹数值仿真模型，分析了无人机不同旋翼间距及转速下受来流干扰的非定常气动特性。杨海涛等[8]利用多重参考系法建立小型双旋翼数值模型，分析了双旋翼在悬停状态及前飞状态下的气动特性变化规律，并与单旋翼进行对比。许和勇等[9]基于非结构嵌套网格方式，通过求解可压缩Euler方程组对涵道旋翼系统的非定常流场进行了动态数值模拟，并进一步研究了桨尖间隙、桨位置、涵道尾叶扩张角度系数等参数变化的动态影响规律。

上述研究工作对共轴旋翼气动特性的变化规律及流动机理的揭示具有重要的指导意义，但将共轴双旋翼进行耦合分析的案例却很少。耦合场用来分析两个或两个以上物理场间的相互作用[10]，流固耦合即流体与结构的耦合分析，在船舶行业中常通过流固耦合方法分析螺旋桨，该方法也可用于分析无人机旋翼，应力与变形对无人机旋翼的影响也不容忽视。本文通过流固耦合方法建立共轴双旋翼的Fluent仿真模型及瞬态结构模型，计算并分析不同转速对共轴双旋翼拉力、应力、变形的影响规律及共轴双旋翼流场、结构场的特征。

1 数学模型

1.1 流体控制方程

质量守恒定律和动量守恒定律是表达流体流动现象的基本定律。对于本文研究的双旋翼流场，假定流体不可压缩，其质量守恒方程与动量守恒方程分别为

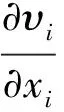
(1)

(2)

1.2 固体控制方程

求解结构场的方程为结构动力学通用方程，具体为

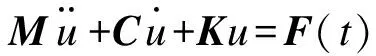
(3)

1.3 流固耦合控制方程

考虑旋翼的流固耦合效应时，通过两相耦合交界面上的平衡及协调引入耦合作用[11]。在固定坐标系下，旋翼以恒定转速绕旋转轴转动的运动方程为

(4)

1.4 湍流模型

湍流模型采用由Menter F R[12]提出的剪切应力传输(Shear Stress Transport，SST)k-ω模型，该模型将传统的k-ω计算模型与k-ε计算模型以加权平均的方式相结合，兼具k-ε模型对远场条件依赖性较小及k-ω模型对近壁面模拟精度相对较高等特点[13]。湍流模型表示为

(5)

(6)

式中：k为湍流动能；ω为湍流耗散率；P为湍流动能的生成项；β*和β为常数系数；β*ρkω和βρω2为耗散项；Dk和Dω为k、ω的扩散项；Cω为交叉扩散项；方程左侧两项分别为瞬态项和对流项。

2 计算模型与设置

2.1 双旋翼几何模型

本文双旋翼选用T-motor 34寸桨叶，桨叶数为2，桨模直径为868mm，桨距角为11°，工作转速为1600～2500rpm，额定转速为1900rpm。根据设计要求，两个旋翼方向不同的桨叶上下排布，组合成共轴双旋翼。采用三维建模软件Creo Parametric建立装配体，如图1所示。根据经验取值，上下两旋翼的间距取为9mm。

图1 共轴双旋翼三维模型

2.2 流体计算模型

采用Fluent Meshing模块进行流体计算域的网格划分。流体计算域包含一个外部静止域和两个内部旋翼旋转域，如图2所示。

图2 流体计算域

对外部静止流体域和内部旋翼旋转域使用多面体网格划分。上下旋转域网格最小尺寸为0.1mm，最大尺寸为5mm，在旋翼附近加密网格，并生成3层边界层网格，上下旋转域网格数量各为363859个。静止流体域网格最小尺寸为5mm，最大尺寸为20mm，在与旋转域交界面位置保持尺寸基本一致，在靠近内域做适当加密，网格数量为255499个。网格扭曲比小于0.8，满足流体分析网格质量要求。流体计算域网格划分如图3所示。

图3 流体计算域网格划分

2.3 瞬态结构计算模型

本文采用单向流固耦合方法，在Ansys Workbench软件中选择Transisent Structural模块，将Fluent模块的计算结果直接导入。在结构上只考虑旋翼流固耦合下的变形特征，不考虑离心力和重力对桨叶变形的影响。采用Ansys Mechanical自带网格划分模块对桨叶模型进行实体网格划分，设置单元尺寸为10mm，并在叶根处进行局部尺寸加密，最终实体网格数为336044，平均单元质量为0.82932。瞬态结构网格划分如图4所示。在中心处设置对地面坐标系的旋转约束，下旋翼顺时针旋转，上旋翼逆时针旋转。

图4 瞬态结构网格划分

本文选取材料是由丙烯腈、丁二烯和苯乙烯三种单体共聚而成的ABS塑料，在材料库中建立ABS塑料，其材料属性如表1所示。

表1 ABS塑料参数表

2.4 流固耦合设置

单向流固耦合只考虑流体对固体的作用，认为固体的变形量不足以对流体部分产生较大影响，故单向流固耦合只需进行一次数据传递，将Fluent的计算结果传递给Transisent Structural即可，再将两数据整合。Ansys Workbench流程如图5所示。

图5 Ansys Workbench流程图

3 计算结果分析

3.1 旋翼气动性分析

3.1.1 旋翼拉力分析

在Fluent模块中，采用多重参考系法，应用SSTk-ω湍流模型分别计算单旋翼和双旋翼的气动性能，设定旋转速度分别为1700、1900、2100、2300、2500rpm，得到旋翼拉力的仿真结果，并与共轴无人机动力系统试验台[14]测得的试验值进行对比，如图6所示。

图6 不同转速下拉力对比

由图6可知，仿真结果与试验值相比较，单旋翼误差最大值为0.77%，双旋翼中上旋翼误差最大值为0.75%、下旋翼误差最大值为0.9%，均小于1%，仿真结果比较可靠。共轴双旋翼的拉力均随旋翼转速的提高而增大，且相同转速下上旋翼的拉力高于下旋翼的拉力；当旋翼转速由1700rpm提高到2100rpm，上旋翼和下旋翼的拉力分别增加58.9%和26.5%；当转速由2100rpm提高到2500rpm，上旋翼和下旋翼拉力分别增加12.6%和10.5%。单旋翼的拉力亦随转速的增加而增大，且双旋翼的上、下旋翼拉力均低于同转速下单旋翼的拉力，说明双旋翼中上旋翼和下旋翼之间存在一定的干扰，单个上旋翼或下旋翼的工作效率低于单旋翼，但上、下旋翼的拉力之和大于单旋翼。

3.1.2 旋翼流速分析

仿真计算得到额定转速下共轴双旋翼的速度云图，如图7所示。

图7 共轴双旋翼流速云图

由图7可见，旋翼上方流速呈伞形分布，离旋翼越近的区域流速越大；下旋翼下方的下洗流速度最大，并垂直向下延伸，流速逐渐衰减；下洗流的速度云图呈U型对称分布，下旋翼部分下洗流受到上旋翼的影响，使下旋翼的尾迹涡向中心收拢。

3.1.3 旋翼压强分析

仿真计算得到额定转速下相同相位角时桨尖和0.8倍半径(0.8R)处的压强云图，如图8所示。

图8 压强分布云图

由图8a可见，无论是上旋翼还是下旋翼，下翼面的压强均大于上翼面，在上翼面出现压力最小值，且上旋翼压强差明显大于下旋翼，这是因为上旋翼的尾流覆盖了下旋翼的工作区域，使下旋翼的气动效果产生负面影响；图8b中压强分布规律与图8a相似，值得注意的是上、下旋翼的迎风处出现压力最大值。

3.2 气动力对旋翼强度的影响

在Ansys Workbench平台上通过流固耦合方法将流场计算得到的旋翼表面压力传递到瞬态结构的旋翼实体上，计算并分析ABS材料旋翼的强度。计算中对桨毂施加绕中心轴的旋转约束，并保持流场中相同的旋翼转速及求解时间，求解得到不同转速下旋翼的最大应力及最大变形，结果如图9所示。

图9 最大应力及最大变形曲线图

由图9可见，随着转速增加，最大应力与最大变形均逐渐减小，符合一般规律。

仿真计算得到额定转速下双旋翼的应力与变形分布云图，如图10和图11所示。

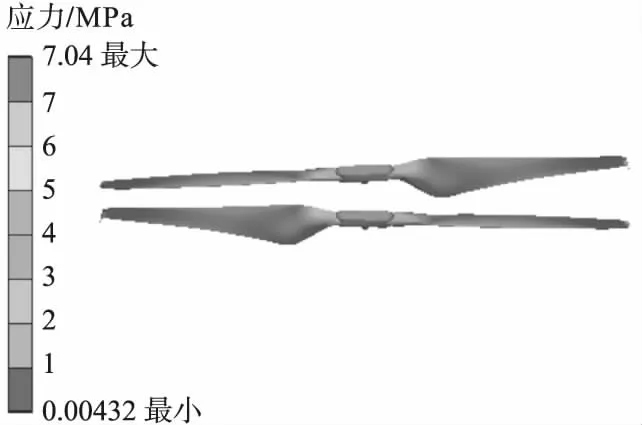
图10 双旋翼应力分布云图

图11 双旋翼变形分布云图

由图10可见，最大应力值在叶根处，沿径向逐渐减小，到叶尖处达到最小值，这说明在旋翼旋转过程中，叶根区域最容易断裂，故在旋翼的设计与选材时，要保证叶根有足够强度。由图11可见，最大变形量在叶尖处，沿径向逐渐增加，到叶根处达到最小值，变形方向均沿中心轴方向，向上变形量远大于向下变形量，说明在旋翼旋转过程中，叶尖处上下挥舞幅度大，一定程度上影响飞行的稳定性。

4 结论

(1)通过三维建模软件建立了共轴双旋翼的几何形态，分别导入Fluent模块和Transisent Structural 模块，联立后实现单向数据传输，确定了单向流固耦合的总流程。

(2)采用多重参考系法分析了共轴双旋翼气动特性，结果显示双旋翼和单旋翼拉力均随转速增加而增大，双旋翼的上、下旋翼拉力均低于同转速下单旋翼拉力，但双旋翼拉力总和大于单旋翼拉力，下旋翼受上旋翼尾流影响，其工作效率降低，上旋翼气动性优于下旋翼。

(3)结构场分析表明，共轴双旋翼的应力变化规律与变形规律恰好相反，叶根处应力最大、变形最小，叶尖处应力最小、变形最大，较小的压力也可产生较大的变形。