基于KCF的微型无人机目标跟踪方法研究

冯迎宾，杨 昆，周 宇，王 典

(1.沈阳理工大学 自动化与电气工程学院，沈阳110159； 2.中国兵器科学研究院，北京 100089)

无人机具有成本低、结构简单、便于操控等特点[1]，被广泛应用于电力巡检[2]、农业生产[3]、军事勘察[4]等领域。由于微型无人机(Miniature Unmanned Aerial Vehicle，MAV)在机动性、灵活性和隐蔽性等方面具有极强的优势，广泛用于侦查与跟踪地面目标。

随着人工智能与计算机视觉技术的发展，基于视觉的无人机目标跟踪技术成为当前的研究热点。针对图像处理效率低的问题，文献[5]提出了基于相关滤波的最小输出误差平方和(Minimum Output Sum of Squared Error，MOSSE)算法，该算法提高了图像目标跟踪的运算速度。在MOSSE算法基础上，文献[6]提出了基于循环结构核(Circulant Structure of Tracking-by-Detection with Kernels，CSK)跟踪算法，通过引入循环矩阵以及核函数简化了运算过程，但由于采用单通道灰度特征对目标进行描述，该算法特征表达能力有限。文献[7]提出了跟踪-学习-检测(Tracking Learning Detecting，TLD)算法，该算法能够对目标进行不断学习以获取目标最新的外观特征。采用跟踪和检测相结合的策略，保证了即使目标外观发生变化也能够持续跟踪。此外，文献[8]首次将目标跟踪问题转换为布丁块匹配问题，利用孪生神经网络提取目标特征点以实现目标跟踪。在孪生神经网络的基础上，文献[9]提出了端到端的全卷积孪生网络目标跟踪(Fully-Convolutional Siamese Networks，SiamFC)算法，该算法采用全卷积神经网络实现目标的快速搜索。文献[10]将目标检测区域生成网络与孪生神经网络目标跟踪算法相结合，提出了孪生区域网络(Siamese & Region Proposal Network，SiamRPN)，将相似度计算问题转化为分类与回归问题，提高了目标跟踪精度。以上目标跟踪算法均通过计算机仿真验证，获得了较好的目标跟踪效果。但基于神经网络的目标跟踪算法计算量较大，不能直接应用于计算能力有限的MAV中。

针对MAV目标跟踪过程中存在的控制器计算能力有限的问题，提出基于单目视觉的无人机目标跟踪控制方法。该方法采用核相关滤波(Kernelized Correlation Filters，KCF)算法快速搜索图像中的目标位置，通过坐标转换矩阵实现目标轨迹的解算，最后将解算出的目标位置发送到无人机飞控系统，完成对目标的跟踪。

1 目标跟踪

KCF目标跟踪算法流程如图1所示。

图1 KCF目标跟踪算法流程图

KCF算法是基于在线学习的判别式目标跟踪算法，将初始帧通过循环矩阵移位的方式生成训练样本序列，并提取样本的方向梯度直方图(Histograms of Oriented Gradients，HOG)特征获取正负样本，以区分目标与背景，通过岭回归训练分类器对目标进行检测，响应值最大的区域即为目标所在区域，并将新的目标区域作为下一帧的训练样本对分类器进行更新[11-12]。虽然KCF算法在目标跟踪过程中需通过循环矩阵生成多个虚拟样本，并且在训练分类器的过程中存在大量的矩阵求逆运算，但算法利用循环矩阵可以对角化的性质，使用离散傅里叶矩阵对样本集合进行对角化。由于对角矩阵运算只需计算对角线上的非零元素，极大减少了对机载计算机CPU和内存资源的占用。此外，KCF算法引入了高斯核函数将非线性问题映射到高维空间并转换为线性问题，极大提高了运算速度，满足了MAV在跟踪过程中对算法快速响应和轻量化的需求。

1.1 循环矩阵

由于每帧图像只有一个基础样本，可通过循环矩阵对基础样本进行行平移获得更多训练样本。将图像对应的二维矩阵变换为n×1维向量得到基础样本x=(x1，x2，…，xn-1，xn)，利用置换矩阵P对样本向量x进行循环移位n次，即可获得当前帧的训练样本矩阵

(1)

利用循环矩阵可对角化的性质，使用离散傅里叶矩阵对样本集合进行对角化。

(2)

1.2 特征提取

在跟踪过程中，需要对目标区域图像提取适当的特征表达和目标描述，以达到有效区分目标和背景的目的。KCF算法使用HOG作为目标特征，该特征可以有效区分目标轮廓边缘与背景的灰度值变化。在提取的过程中，先将目标图像进行灰度化和归一化处理以减小光照变化和噪声带来的影响，再计算图像中各个像素点(a，b)的梯度值，计算过程为

(3)

式中：G1(a，b)、G2(a，b)分别为像素点(a，b)在水平和垂直方向的梯度值；I(a，b)为像素点(a，b)对应的灰度值。梯度幅值G(a，b)和梯度方向β(a，b)分别为

(4)

本文根据参考文献[13]统计梯度直方图得到目标图像最终的HOG特征。

1.3 训练分类器

设训练样本为xi，回归标签为yi，使用最小二乘法训练分类器f(x)=ωTx(ω为分类器权重系数)，使训练样本xi与回归标签yi之间平均误差最小，如公式(5)所示。

(5)

式中λ为正则项系数。为提高分类器的泛化能力，防止分类器出现过拟合现象，加入正则项λ‖ω‖2控制过拟合。令ω的偏导数为零，求得ω的表达式为

ω=(XTX+λI)-1XTy

(6)

式中：I为单位矩阵；y为各样本回归标签yi组成的列向量。将式(6)转换到复数域得

ω=(XHX+λI)-1XHy

(7)

将经过傅里叶变换后的样本矩阵X带入式(7)，得到频域中的计算公式为

(8)

1.4 核方法

由于目标跟踪为非线性问题，将样本x通过映射函数φ(x)映射到高维空间可使非线性问题变为线性可分，而分类器的权重系数ω可表示为样本映射后的线性组合

(9)

式中αi为线性组合系数。将式(9)带入分类器中求得回归函数为

(10)

式中：k(xi，xj)=kxixj=φT(xi)φ(xj)，为核函数；xi、xj分别表示当前帧和下一帧样本。KCF算法采用高斯核函数，将k(xi，xj)组合成大小为n×n维的核函数K，此时K满足循环矩阵特性。

将式(10)带入式(5)可导出由αi组成的系数向量α的表达式为

α=(K+λI)-1y

(11)

对式(11)进行傅里叶变换，得

(12)

1.5 目标检测与更新

在检测阶段，需要计算测试样本序列与在线分类器的相关响应以确定当前帧的目标位置。设x为当前帧训练样本序列，z为下一帧测试样本序列，用kxz表示x和z的核函数，在频域中对响应进行求解

(13)

响应的最大值即为预测的当前帧目标位置。

确定新的目标位置后，将当前目标区域作为训练样本对分类器进行一次更新得到新的检测模型，以此实时修正跟踪框，直到视频帧播放完毕。

2 目标位置计算

2.1 目标图像模型

MAV在目标跟踪过程中，如何估计目标点在世界坐标系下的位置是实现目标跟踪的先决条件。为实现目标位置解算，需要将MAV、单目相机转化到目标位置所在的世界坐标系下。MAV、单目相机以及目标在世界坐标系的相对位置向量关系如图2所示。

图2 MAV、相机及目标的相对位置向量关系

PN=P1+P2+P3

(14)

2.2 位置解算

(15)

(16)

即该旋转矩阵的值可根据MAV的姿态转换得到。

目标到相机的距离关系向量P3需通过像素坐标、图像坐标、相机坐标之间的转换关系求解。假设目标点N在图像坐标系下的坐标为(xu，yv)，则在像素坐标系下的坐标(u，v)可表示为

(17)

式中：(u0，v0)是图像坐标系原点在像素坐标系下坐标；dx，dy分别表示单位像素的长和宽，单位为mm。式(17)可用矩阵表示为

(18)

(19)

式中f为相机焦距，综合式(18)和式(19)可知像素坐标系与相机坐标系关系为

(20)

(21)

根据相机在无人机的安装位置，可将相机坐标系下目标点位置向量cP3经平移转换到机载坐标下的位置，机载坐标下的位置经过旋转变换得到世界坐标系，则向量P3与cP3有如下关系

(22)

综上，式(14)可转化为

(23)

图3 相似三角形距离估计原理示意图

(24)

(25)

2.3 期望偏航角计算

在跟踪过程中为使目标中心始终保持在图像中央，需计算目标相对于相机运动的夹角，该角即为无人机的期望偏航角。假设目标在当前帧图片的像素点坐标为(d，g)，目标在下一帧图片的像素点坐标为(s，t)，则无人机的期望偏航角计算方法[15]为

(26)

3 无人机目标跟踪流程

无人机目标跟踪方法流程如图4所示。

图4 无人机目标跟踪方法流程图

无人机目标跟踪算法主要包括KCF目标跟踪算法、目标位置解算算法、无人机位置控制算法。目标跟踪算法的目的是从单目相机获取的图像序列中得到目标在图像序列中的像素点位置；目标位置解算算法根据目标在像素点的位置和坐标转换关系计算出目标在世界坐标系OXYZ下的水平位置；无人机位置控制算法根据无人机位置和目标位置的偏差，利用无人机闭环控制器使偏差趋于0，从而实现对目标的跟踪。

4 仿真

MAV对系统的运行逻辑和参数设置有极高要求，任何微小的逻辑或计算错误都会造成微型无人机损坏。在MAV试飞之前利用Gazebo搭建无人机仿真平台，对上述算法进行验证，降低飞行危险，提高开发效率。仿真硬件环境为中央处理器Inter Core i5-6300HQ、主频2.30GHz、内存8G。

仿真实验中，分别以直线和蛇形曲线作为目标的运动轨迹以验证不同情况下无人机轨迹跟踪效果。

4.1 直线轨迹跟踪仿真结果与分析

本组实验中，无人机由(0，0，0)点处起飞至(0，0，1.5)处悬停，目标由(0，0，0)处出发，沿x轴方向以0.3m/s的速度做直线运动，实验结果如图5、图6、图7所示，图中标注1指无人机跟踪轨迹，标注2指目标运动轨迹。

图5为无人机对目标进行直线跟踪的三维轨迹图。

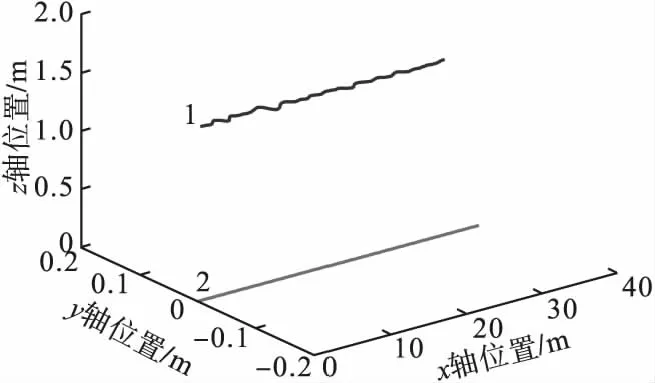
图5 直线轨迹跟踪结果

图6分别给出了无人机沿x、y轴的运动曲线。由图6可见，轨迹跟踪效果良好。

图6 沿x、y轴直线运动轨迹跟踪结果

图7为无人机沿x轴和y轴方向的跟踪误差。

图7 沿x、y轴直线运动轨迹跟踪误差

由图7可见，无人机沿x轴最大跟踪误差出现在99s左右，最大误差为0.254m，误差最终稳定在0.2m左右。沿y轴跟踪最大误差为0.089m，并最终稳定在0.03m左右。

4.2 蛇形运动轨迹跟踪仿真结果与分析

本组实验中，无人机由(0，0，0)点处起飞至(0，0，1.5)处悬停，目标由(0，0，0)处出发，沿x轴方向以0.3m/s的速度做蛇形运动，实验结果如图8、图9、图10所示，图中标注1指无人机跟踪轨迹，标注2指目标运动轨迹。

图8为无人机对目标进行蛇形运动跟踪的三维轨迹图。

图8 蛇形运动轨迹跟踪结果

图9分别给出了无人机沿x、y轴的运动轨迹，表明了良好的跟踪效果。

图9 沿x、y轴蛇形运动轨迹跟踪结果

图10为无人机沿x轴和y轴的跟踪误差。

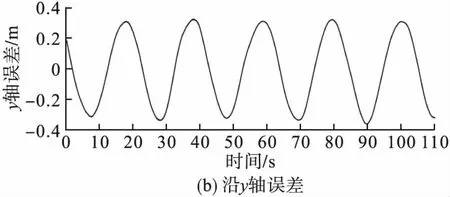
图10 沿x、y轴蛇形运动轨迹跟踪误差

由图10可见，沿x轴最大跟踪误差出现在42s左右，最大误差为0.26m，误差最终稳定在0.15m左右。沿y轴最大误差为0.36m，并最终稳定在0.35m左右。

图11和图12给出了无人机跟踪过程中偏航角及其与期望偏航角的误差。图中标注1为无人机偏航角，标注2为期望偏航角。由图12可见，偏航角最大误差为0.092rad，且误差稳定在0.08rad左右。

图11 偏航角与期望偏航角

图12 偏航角误差

目标跟踪过程中，KCF算法处理每帧图片平均耗时约6.3ms，在目标位置解算过程中，算法耗时2ms，而相机的采样频率为30Hz，因此该算法完全满足运动目标的实时跟踪。

5 结论

提出了基于KCF算法的MAV目标跟踪控制策略，并利用Gazebo仿真环境进行了目标跟踪实验。实验结果表明，提出的运动目标跟踪策略可实现对运动目标的实时跟踪，具有良好的跟踪效果。下一步研究将提出的算法移植到MAV平台，完成算法的实际测试。