空间分数阶对流方程的格子Boltzmann方法*

魏雪丹,李梦军,戴厚平

(吉首大学数学与统计学院,湖南 吉首 416000)

对流是由流体粒子的整体运动和流体分子的随机运动形成的热量、质量和动量传递[1],经典的对流扩散问题在不考虑扩散过程时是纯对流问题.目前,对流方程广泛应用于泥沙运移、污染物输送等实际问题中[2-5].但是在复杂不均匀介质中,由于不同介质之间的相互作用,传统的整数阶对流方程已不能准确刻画复杂流体的演化过程.随着分数阶微分理论的发展,人们逐渐发现分数阶微积分算子的非局部性能够很好地刻画具有时间记忆和全局依赖特点的演化过程,于是分数阶对流方程应运而生.然而,也正是分数阶微分算子的全局相关性,使得大多数分数阶微分方程的精确解不能显式表达,从而数值解逼近精确解在分数阶微分方程求解方面越来越重要[6-11].对于空间Caputo型分数阶微分方程,陈雪娟等[12]运用二次多项式样条函数数值求解了一类空间分数阶Fisher方程.为了进一步拓展空间Caputo型分数阶微分方程的数值解法,笔者拟考虑一类分数阶对流方程,利用积分中值定理和线性插值方法将分数阶对流方程转化为标准对流方程的形式,运用格子Boltzmann方法(Lattice Boltzmann Method,LBM)进行数值求解.

1 分数阶对流方程的格子Boltzmann方法

1.1 分数阶对流方程

考虑如下形式的分数阶对流方程：

(1)

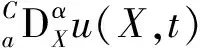
事实上,由于Caputo型分数阶导数与Riemann-Liouville分数阶导数二者可以相互转化,因此方程(1)也可以表示为

1.2 积分离散化

1.3 格子Boltzmann方法

分布函数采用如下形式的演化方程：

(2)

(3)

根据Chapman-Enskog多尺度展开分析,引入二阶时间尺度和一阶空间尺度,并将g(X,t)展开到二阶,可得

(4)

(5)

g(X,t)=ε2g(2)(X,t).

(6)

在小Knudsen数ε的假设下展开fi(X,t),可得

(7)

将方程(3)～(7)代入方程(2),可得

(8)

比较方程(8)两边ε的各阶系数,ε的系数

(9)

ε2的系数

(10)

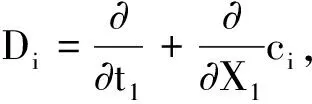
(11)

将方程(11)代入方程(10),可得

(12)

(13)

(14)

(15)

将方程(9)和方程(12)在i方向上求和,并恢复到原尺度,可得

对于一维分数阶对流方程,采用D1Q3 LB模型求解,由方程(13)～(15)可求得平衡态分布函数的表达式为

对于二维分数阶对流方程,采用D2Q5 LB模型求解,由方程(13)～(15)可求得平衡态分布函数的表达式为

2 数值算例

为了量化格子Boltzmann模型的精确性,引入误差检验公式,全局相对误差(Global Relative Error，用EGRE表示)和最大误差(Maximum Error，用EME表示)分别定义为

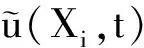
问题1在有限区间[0,1]上考虑方程(1)的一维初边值问题，其初边值条件为

源项为

验证该一维初边值问题的精确解u(x,t)=x2(1-x)2et.

取参数k=0.001,τ=1.95,Δt=0.001,N=64,此时全局相对误差见表1.由表1可知：相同时间T,随着分数阶α的增加,全局相对误差逐渐增加；相同分数阶α,随着时间T的增加,由于误差的累计,全局相对误差逐渐增加,但误差范围基本保持在10-3以内.

表1 问题1在N=64时的全局相对误差

当T=1,Δt=0.001时，不同分数阶α对应的空间最大误差及其收敛阶见表2.由表2可知,LBM在空间方向收敛.

表2 问题1在T=1,Δt=0.001时的最大误差及其收敛阶

图1示出了α=0.4时不同时刻的数值解与精确解.由图1可见,数值解与精确解吻合较好,且可以长时间保持稳定.

图1 α=0.4时的数值解与精确解

问题2在区间[0,1]×[0,1]上考虑方程(1)的二维初边值问题,其初边值条件为

源项为

验证该二维初边值问题精确解u(x,y,t)=x2y2sint.

取参数k1=k2=0.001,τ=1.25,Δt=10-4,T=0.3,N=100,当α=0.5时数值解与精确解如图2所示,数值解与精确解的绝对误差如图3所示.由图2,3可见,数值解与精确解的全局相对误差为7.888 8×10-4,最大误差为6.188 1×10-4,二者在任意时刻和位置的误差达到10-4数量级.

图2 α=0.5时的数值解与精确解

图3 数值解与精确解的绝对误差

当T=0.1时,不同α和网格数下的全局相对误差见表3.由表3可知：相同α时,随着网格数的增加,全局相对误差逐渐减小,说明LBM在空间上收敛；相同网格数下,随着α的增加,全局相对误差逐渐增加,但控制在10-2以内.

表3 问题2在T=0.1时的全局相对误差

当网格数N=32时,不同时刻和α下的全局相对误差见表4.由表4可知，数值解能较好逼近精确解,进一步说明了LBM的有效性.

表4 问题2在不同时刻和α下的全局相对误差

3 结语

运用构建的格子Boltzmann模型数值求解了一类空间Caputo型分数阶对流方程.运用积分中值定理和线性插值方法将分数阶对流方程转化为标准对流方程,使得分数阶算子产生的记忆部分保留在源项中,极大地简化了数值计算过程.数值解与精确解的实例比较结果表明,格子Boltzmann模型可以有效地求解Caputo型分数阶对流方程.本研究可以推广到空间三维问题及时间分数阶对流问题,进而拓展LBM在分数阶微分方程数值解求解方面的应用.