具有瞬时与非瞬时脉冲效应害虫治理切换模型的动力学性质分析

薛 枫,李金洋，刘 兵

(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

在自然界中，不同生命阶段的害虫其生理机能差异显著,因此，害虫通常具有阶段结构[1-5]，一般将其分为成虫与幼虫.成年种群每年只在某些固定时刻生育产卵且繁殖力惊人.如褐飞虱一年可以繁殖18～30代，每头雌虫一次可以产卵200～700粒，多者超过1 000粒；米虫一年可以繁殖7代左右，每头雌虫一次产卵可达500粒.因此，TANG[6]利用脉冲微分方程理论，刻画了这种生育现象，建立了具有脉冲生育的单种群阶段结构种群模型.在此基础上，文献[7]考虑采用化学控制治理害虫，通过在害虫种群的每一生育周期的固定时刻喷洒杀虫剂，其假设杀虫剂只是瞬时成比例杀死成虫，建立害虫治理生育脉冲阶段结构模型，结果表明，在每个生育周期成虫生育前喷洒杀虫剂对害虫的控制效果最好.文献[8]分析了杀虫剂对幼虫或成虫具有杀死作用以及同时杀死幼虫和成虫的种群动力学行为，得到系统平衡态稳定的阈值条件，以及喷洒杀虫剂的最优时刻.但是，上述研究都是假设杀虫剂是瞬时成比例地杀死害虫.事实上，由于杀虫剂具有残留作用,杀虫剂对害虫具有瞬时作用和接下来的一段时间内持续的非瞬时脉冲作用，相较于以往的工作并没有考虑这个问题.

本文建立了切换策略下具有瞬时与非瞬时脉冲效应的一类生育脉冲害虫治理模型，分析其动力学性质和重要参数对害虫治理的影响.

1 模型建立

害虫种群分为成虫阶段和幼虫阶段，假设成虫在每年的固定时刻产卵,同时假设在害虫繁殖之后的某个固定时刻喷洒杀虫剂.实际上,杀虫剂在喷洒瞬间大量杀死害虫之后,仍对害虫产生一个非瞬时的残留作用,因此，建立如下模型：

(1)

其中,x表示幼虫,y表示成虫;x(t-),y(t-)表示脉冲前的种群密度;x(t+),y(t+)表示脉冲后的种群密度;α表示幼虫向成虫的转化率;d表示害虫的死亡率;p1表示杀虫剂对幼虫的瞬时杀死率,p2表示杀虫剂对成虫的瞬时杀死率;l表示一个生育周期内喷洒杀虫剂的最初时刻,这里0d.

2 模型分析

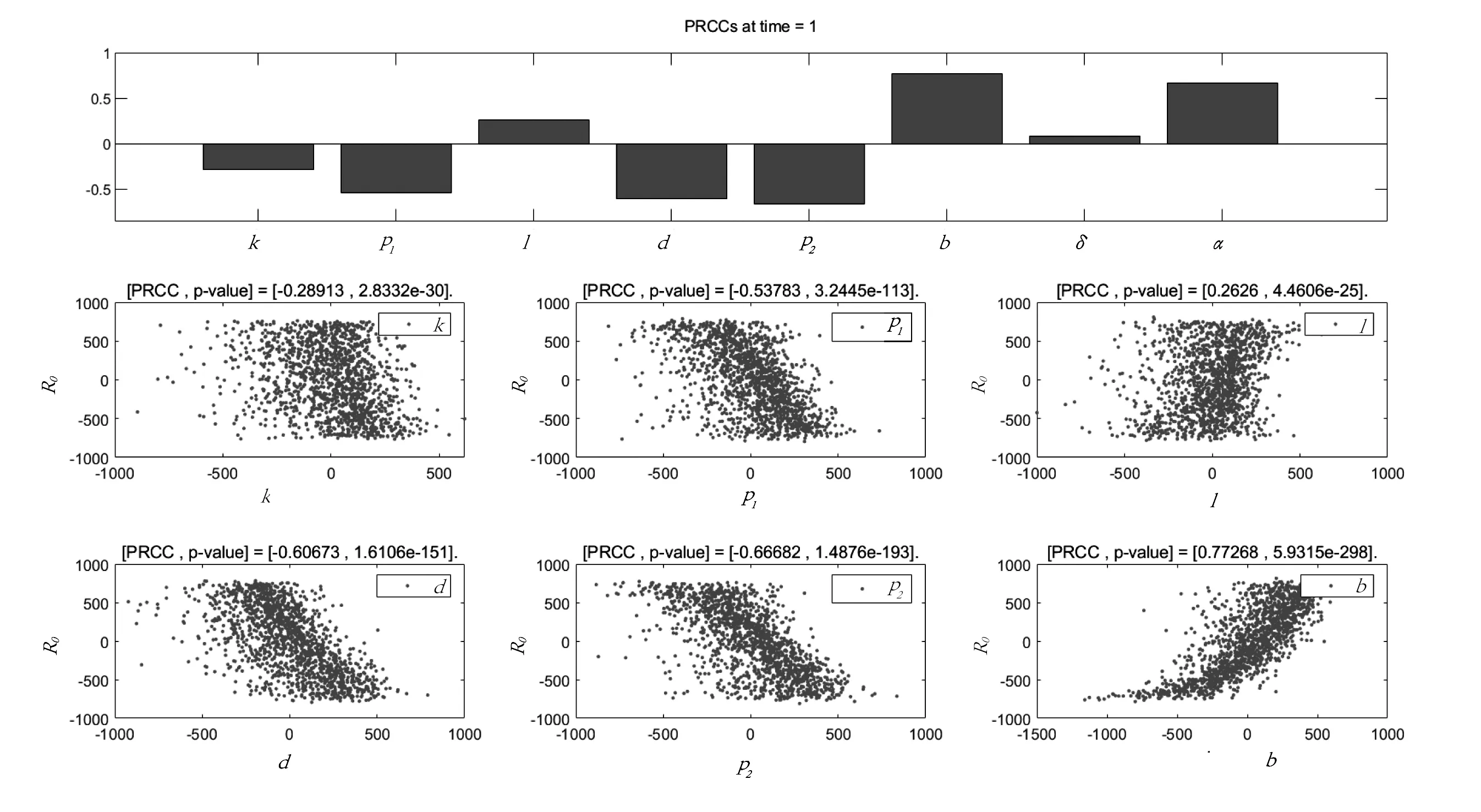
首先,对模型(1)进行求解.当m≤t

两边分别积分

得到

x(t)=x(m+)e-(d+α)(t-m).

将模型(1)中第1个与第2个方程相加：

两边分别积分

得到

y(t)=x(m+)(e-d(t-m)-e-(d+α)(t-m))+y(m+)e-d(t-m),

在t=(m+l)时刻喷洒杀虫剂,得

当

m+l≤t

时,由系统(1)的方程

得

将系统(1)中第5与第6个方程相加：

得

因此，当t=(m+1)时,

其中

y((m+1)-)=

[x(m+)e-dl((1-p1)e-αl+(1-e-αl)(1-p2))+y(m+)e-dl(1-p2)]e-d(1-l)·

A-x(m+)(1-p1)e-(d+α)·A,

记

x(m+)=xm,

y(m+)=ym,

则当t=(m+1)+时,害虫种群发生生育脉冲,得到如下差分方程

(2)

这里

A*=e-dl((1-p1)e-αl+(1-e-αl)(1-p2)),

B*=(1-p2)e-dl,(0

C*=(1-p1)e-(d+α)·A,(0

D*=e-d(1-l)·A,(0

接下来,分析差分方程(2)平衡点的稳定性,从而得到模型(1)的动力学性质.

定理1当0

证明由系统(2)得到平凡平衡态(0,0)处的矩阵为

经计算得到矩阵的行列式

detA(0,0)=B*C*D*,

矩阵的迹

trA(0,0)=C*+b(A*D*-C*)+B*D*,

这里

A*D*-C*=(1-p1)·A·(e-αl-d-e-α-d)>0,

所以

1-detA(0,0)>0,

1+detA(0,0)+trA(0,0)>0.

要想满足Jury判据,需满足

1-trA(0,0)+detA(0,0)>0,

即

(3)

因此,当0

令

由不等式(3)可知，01时,系统(2)存在正平衡态(x*,y*),其中，正平衡态满足方程

解得

定理2当b0

证明系统(2)存在平衡态(x*,y*)处的矩阵为

其中

W21=A*D*-C*,

W22=B*D*.

化简得行列式的值

行列式的迹

这里

1-trA(x*,y*)+detA(x*,y*)=(1-C*)(1-B*D*)lnR0>0,

且

1-detA(x*,y*)>0,

从而要想

1+trA(x*,y*)+detA(x*,y*)>0,

则需满足b0

因此,当b0

3 数值模拟

如果固定其他参数,选择b为分支变量,由定理1和定理2知害虫种群灭绝或持续生存依赖于参数b的变化.

如果0

如果b0

如果参数b继续增加,那么正周期解的稳定性被破坏,系统(1)将呈现非常复杂的倍周期分支到混沌现象，如图1所示.

图1 参数b对系统(1)的种群x(t)、y(t)影响分支图，其他参数：α=0.5,d=0.2,k=0.2,l=0.1,δ=0.4,p1=0.6, p2=0.7,x0=2,y0=0.6

为了确定影响害虫控制策略的关键因子,对R0及其参数进行了敏感性分析[9-10].敏感性分析是一种对复杂模型的量化不确定性分析的方法.通过计算参数的PRCC值,分析了参数对R0的敏感性,确定了影响阈值的关键参数.

当参数的PRCC值为正时,该参数与R0正相关,这意味着阈值R0随参数的增加而增加；相反地,当参数的PRCC值为负时,该参数与R0负相关,这意味着阈值R0随参数的增加而减小.

进一步有如下规定:如果|PRCC|>0.4,则表示输入参数和输出变量之间存在强相关性,即该参数对R0的影响大；如果0.2<|PRCC|<0.4,则该参数对R0有中等影响；如果|PRCC|<0.2,则该参数对R0的影响较弱.

从图2可以看出,参数l,b,δ,α与阈值R0是正相关的.因此,这些参数的增加会使得R0增加,进而使得害虫种群数量增大,不利于害虫的控制.参数k,p1,p2,d与阈值是负相关的,随着k,p1,p2,d的增加,R0减小,这有利于害虫的控制.同时,通过图2可以看到,阈值R0受杀虫剂对幼虫的瞬时杀死率p1、杀虫剂对成虫的瞬时杀死率p2、害虫种群的生育率b、害虫的死亡率d以及转化率α影响较大,这些参数对害虫治理起到了关键的作用.

图2 主要参数关于阈值R0的PRCC值和PRCC值关于参数k,p1,l,d,p2,b散点图，样本量为1 500且所有参数同时变化， 其中基本参数为α=0.5,d=0.2,k=0.2,l=0.1,δ=0.4,p1=0.6,p2=0.7,b=20

4 结论

本文建立一个具有瞬时与非瞬时脉冲效应的一类生育脉冲害虫治理切换模型.这里利用连续负指数函数模拟杀虫剂的残留作用,采用 Ricker 生育函数刻画脉冲生育现象.利用脉冲微分方程、Jury判据等相关知识,研究模型(1)害虫种群的动力学性质.通过理论分析得到害虫种群灭绝或种群持续生存的阈值条件：当R0<1时,模型(2)存在局部渐近稳定的平凡平衡态,即害虫种群将会灭绝;当R0>1时,模型(2)的正平衡态是局部渐近稳定的,即害虫种群将会持续生存.此外,通过数值模拟发现，模型有复杂的动力学行为,包括倍周期分支和混沌现象.通过对主要参数进行敏感性分析发现,杀虫剂对幼虫的瞬时杀死率p1、杀虫剂对成虫的瞬时杀死率p2、害虫种群的生育率b、害虫的死亡率d以及转化率α对害虫灭绝或持续生存起着关键作用.