基于GARCH模型的农产品期货套期保值绩效评估研究

于 刚,赵冬斌

(东北财经大学 金融学院，辽宁 大连 116025)

随着时代的发展，农业生产方式正在不断进步，其生产量以及作物质量也在不断提高.农产品贸易的发展顺应了这种生产上的进步，从先生产后找市场到远期合约的产生，这种生产经济模式的转变让农户的风险大大降低，可以更好地适应市场需要，避免了盲目生产.在这种远期合约的基础上，由期货交易所进行合约的标准化就形成了现在的农产品期货合约.

辽宁围绕粮油、蔬菜、水果、畜牧、水产、特色农产品等产业优势，积极培育壮大农产品区域公用品牌和农产品品牌.截至2018年底，辽宁名牌农产品达到218个，绿色产品企业491家.在发展农产品的同时，农户及企业利用金融衍生工具规避风险的意识也越来越强.我国农产品期货起步较晚，规模也较小，但随着大众金融意识的提高，农产品期货市场的流动性以及普及度也正逐步增大.目前，很多涉农企业使用农产品期货进行套期保值，极大降低了其自身承受的价格波动风险.但相较于其他发达国家的金融市场，我国期货市场套期保值的绩效偏低，即降低风险的程度较小，这对于期货市场的发展是不利的.所以，对农产品期货的套期保值绩效进行研究并提升，是引导农产品期货市场发展重要的一步.

最早提出期货最优套期保值比率的是JOHNSON(1960年)[1].他指出最优套期保值比率是在收益方差最小时得到的，并可以用OLS模型进行估计.随着时间序列分析的发展，OLS模型的缺点被提出.学者指出使用OLS模型对最优套期保值比率进行估计会受到残差项序列相关的影响，于是MYERS等(1989年)[2]提出了双变量向量自回归模型进行估计，消除序列自相关的影响.由于上述两种模型注重的均为短期波动，并未包含长期关系，于是LIEN(1996年)[3]提出包含协整关系的误差修正模型.OLS模型的另外一个缺点是无法解决异方差问题，于是GARCH模型被PARK等(1995年)[4]在估计最优套期保值比率时使用，用于得到时变的最优套期保值比率.在对最优套期保值比率的确定方法进行研究的基础上，学者们开始了对套期保值绩效的研究.LIEN(2006年)[5]对套期保值绩效的估计偏差进行了讲述，LIEN等(2002年)[6]探讨了使用常数相关的GARCH模型对套期保值绩效进行估计的结果.

由于我国期货市场起步较晚，发达程度不高，所以国内学者普遍采用现有模型进行实证研究和绩效分析.彭红枫等(2007年)[7]在研究铜期货的最优套期保值比率以及相应绩效时，利用了OLS模型以及二元GARCH模型，估计出铜期货的最优套期保值比率，并将各自的绩效值进行了比较，得出了二元GARCH模型具有较好的套期保值效果的结论.杨浩(2007年)[8]在研究沪深300股指期货的套期保值效果时，分别使用了动态策略和静态策略两种方法.对于沪深300股指期货的动态策略套期保值效果，他使用了CCC-BGARCH模型和DCC-BGARCH模型进行评价；对于静态策略套期保值效果，他使用了OLS模型和VECM模型进行评价，最终得到结论：在动态模型中，DCC-BGARCH模型套期保值效果更好，而在静态模型中，VECM模型更好.顾京等(2013年)[9]使用沪深300股指期货的数据计算最优套期保值比率并评价绩效，在计算最优套期保值比率时，分别使用了OLS、VAR、VECM静态模型和BEEK-GARCH、CCC-GARCH、DCC-GARCH动态模型，而在评价最优套期保值比率的绩效值时，他们分别使用了“风险最小化”和“效用最大化”原则这两种方法，最后得到结论：在“风险最小化”原则下，BEKK-GARCH模型绩效最优；而在“效用最大化”原则下，对于样本内的数据来说，DCC-GARCH模型最优，对于样本外的数据来说，BEKK-GARCH模型最优.陈晨(2016年)[10]在对黄金期货的最优套期保值比率及绩效的研究中，分别使用了OLS模型、ECM模型和ECM-GARCH模型，最后总结出结论：对于黄金期货而言，使用ECM-GARCH模型得到的最优套期保值比率的绩效最优.周振南(2016年)[11]在研究小麦、玉米和棉花的最优套期保值比率及绩效时，使用GARCH模型对最优套期保值比率进行计算，经过对比其绩效，最后得出棉花绩效最好，玉米次之，小麦最差，而且得出三者均低于相同农产品的国际平均水平的结论.黄连蓉(2020年)[12]研究豆粕期货，利用误差修正模型估计最优套期保值比率并计算其绩效.

本文以大豆、豆粕、鸡蛋、玉米4种农产品为例，使用了普通最小二乘法模型(OLS)、双变量向量自回归模型(B-VAR)、误差修正模型(ECM)以及广义自回归条件异方差模型(GARCH)，分别对4种农产品的最优套期保值比率进行计算，并通过“风险最小化”以及“效用最大化”两种方法对最优套期保值比率的绩效进行计算，为在农产品期货市场上进行套期保值以期对冲现货市场风险的农户及涉农企业提供理论和实践参考.

1 套期保值及绩效评价理论模型

1.1 套期保值相关理论分析模型

使用不同的套期保值模型都有一个共同目的，就是求解最优套期保值比率.套期保值比率是指套期保值者所拥有的期货合约头寸总价值与现货头寸总价值之间的比率.当投资者同时拥有期货头寸与现货头寸时，这一套期保值的资产组合，原理上可以实现资产标的物、到期日以及交易金额等条件的设定，使得期货与现货完全匹配，从而达到完全消除组合的价格风险，此时，称这个套期保值为“完美套期保值”.

但现实情况下，不完美的套期保值，即期货、现货不能完全匹配才是最常见到的.一般来说，“不完美”源自两方面，即“数量风险”与“基差风险”.“数量风险”是指由于期货是标准化的合约，可能导致期货与现货的数量不同，出现未被套期保值覆盖的头寸，从而带来风险；“基差风险”是指期货价格与现货价格不同带来的风险，这种不同可能来源于期货的标的资产与现货不同，或套期保值结束时期货合约未到期，期货价格未完全收敛至现货价格.在这种不完美的情况下，才有最优套期保值比率，这个比率一般是指套期保值的资产组合价格变动方差最小时的套期保值比率.

1.2 套期保值模型

根据上述对最优套期保值比率的分析，可以推导出最优套期保值比率的计算方法.使用St表示现货价格，Ft表示期货价格，h表示使用的套期保值比率，则当套期保值者买入套期保值时，需要买入期货合约并持有现货的空头头寸，在套期保值期间，资产组合的价值变化为ΔSt-hΔFt；当套期保值者卖出套期保值时，需要卖出期货合约并持有现货的多头头寸，在套期保值期间，资产组合的价值变化为hΔFt-ΔSt.用σS表示现货收益的标准差，σF表示期货收益的标准差，ρSF表示现货收益与期货收益之间的相关系数，则使用上述两种套期保值策略，在套期保值期间，资产组合的价格变化方差为

最优套期保值比率可以表示为

1.2.1 普通最小二乘法模型(OLS) 当进行估计时，可以采用OLS模型，自变量为期货价格变动，因变量为现货价格变动，根据最小二乘法的计算方法，自变量的系数估计值恰好为上述的最优套期保值比率.

可以采用

ΔSt=c+h*ΔFt+εt，

(1)

对最优套期保值比率进行估计，其中，εt为残差.

1.2.2 双变量向量自回归模型(B-VAR) 通过上述OLS模型得到的最优套期保值比率，常常会受到回归方程残差项自相关的影响.为了消除这种自相关性对结果的影响，可以使用向量自回归的方法.这种方法是将模型中的每一个内生变量当作所有变量若干滞后变量的因变量进行回归.对于期货套期保值，可以对现货价格变动与期货价格变动进行双变量的向量自回归.现货价格变动做回归，表示为

期货价格变动为

其中，Cs、Cf为截距项，αsi、αfi、βsj、βfj为回归系数，εst、εft均为独立同分布的随机误差项.为了完全消除残差项的自相关，需要找到合适的k值.由于ΔSt与ΔFt的滞后项是为了消除残差项自相关而引入的，所以计算最优套期保值比率时也应该将滞后项给方差带来的影响考虑进去，设Ht表示第t期时的信息集，包含着从第t-k期到t-1期现货与期货价格变动的共同影响，最优套期保值比率表示为

同理，根据最小二乘法的计算方法，h*也可以使用方程εst=c+h*εft+γt进行估计.将εst与εft使用向量自回归的方程替换并化简，最终可以得到B-VAR模型：

(2)

1.2.3 误差修正模型(ECM) 向量自回归模型虽然在OLS模型的基础上解决了残差序列可能产生的自相关性对模型造成的影响，但还有其他不足：由于上述一直使用的是现货价格与期货价格的差分项，即现货、期货价格变动量并建立相关关系，这种相关关系只能表达现货价格和期货价格二者之间的短期均衡关系，而忽略了两者的水平值，即不能反映两者的长期均衡关系.另外，我们知道期货价格与现货价格存在静态均衡，即期货价格不变时，现货价格也会保持其长期均衡值不变.有一种情况是：期货价格变动与现货价格变动之间符合ΔSt=α+βΔFt+εt的关系，且α>0，若期货价格变动为零时，则现货价格变动大于零，于是期货价格没变，而现货价格增加，这与二者的静态均衡相违背.

如果在向量自回归模型的期货与现货之间的短期关系之中加入对长期均衡关系(也称协整关系)的表示，将其作为误差修正项，就成了误差修正模型，公式表示为

(3)

其中，Zt-1表示的是误差修正项，求法是：先做出St与Ft之间的协整方程St=α+βFt+Zt，方程中的随机误差项即为Zt.

1.2.4 广义自回归条件异方差模型(GARCH) 上述B-VAR与ECM模型解决的问题是OLS模型的残差自相关性，而考虑期货价格与现货价格之间的模型，除了两种价格，其余的影响价格变动的因素全部被归入了随机误差项，则可能导致随机误差项产生异方差性，即随机误差项的方差不是常数，而是随时间变动的量；另外，期货价格与现货价格这种经济变量，本身会受很多随机因素的影响，比如政策变动、自然灾害或金融危机等，也会带来异方差性.为了解决这种异方差问题，可以使用广义自回归条件异方差模型，用随机误差项时变的方差，即条件方差来代替固定的方差.GARCH模型的阶数一般选择(1,1)就能满足要求，如果滞后阶数过多会导致模型不稳定，本文对期货与现货的价格变动，使用二元GARCH(1,1)模型，公式表示为

(4)

(5)

(6)

其中，

式(4)和式(5)为模型的条件均值方程，与ECM模型的表达式均是在B-VAR模型的基础上增加了误差修正项，这表明GARCH模型是在上述静态模型的基础上，为了解决异方差问题构建的模型，其中，两个式子等号右侧除去随机误差项的部分即为等号左侧变量的条件均值.

式(6)为GARCH(1,1)模型的条件方差及条件协方差矩阵方程，表示t期现货价格变动的条件方差h11t、期货价格变动的条件方差h22t以及二者之间的条件协方差h12t，这也是GARCH 模型主要想表达的内容，即随机误差项的方差是时变的.

而最优套期保值比率按照上文的方法可以表示为

(7)

这个最优套期保值比率是有下角标t的，表示它是时变的值.这种动态的套期保值比率表示投资者根据前期已知信息集，时刻调整自己的套期保值比率，即不断调整所持有的期货合约的数量，从而增强套期保值的效果.为了研究方便，本文在计算套期保值绩效时，选择此最优套期保值比率的平均值来计算.

1.3 套期保值绩效评价

经过上述各模型对最优套期保值比率进行估计之后，得到投资组合中现货期货的投资比例，那么对使用这些套期保值比率时套期保值的实现程度进行评价，就需要估计其套期保值绩效.学术界对于套期保值绩效评价有两种方法:

1.3.1 “风险最小化” 选取最优套期保值比率时，使用使现货与期货的资产组合价格变动方差最小的套期保值比率，即风险最小，于是将套期保值前后的价格变动方差做比较，方差减少程度越大的，套期保值绩效越好.具体的计算方法为：以Ut表示现货价格的变动，即不进行套期保值时现货价格波动导致的每日收益或亏损；以Qt表示用h*作为套期保值比率进行套期保值，现货与期货的资产组合的价格波动导致的每日收益或亏损.用套期保值前的价格变动方差减去套期保值之后的价格变动方差，再除以套期保值前的价格变动方差，表示方差减少程度.则套期保值前的方差可以表示为

Var(Ut)=Var(ΔSt)，

套期保值后的方差可以表示为

Var(Qt)=Var(ΔSt-h*ΔFt)=Var(ΔSt)+h*2Var(ΔFt)-2h*Cov(ΔSt,ΔFt),

套期保值绩效为

(8)

由于方差减少程度越大，风险越小，所以E1越大套期保值绩效越好，又因为方差非负，套期保值之后的方差最小值为零，此时E1值最大为100%，套期保值绩效最好.

1.3.2 “效用最大化” 投资者在追求风险更低的同时，还会追求较高的收益率.因此，将收益率、风险以及投资者的风险厌恶程度结合在一起，考虑整个投资组合对于投资者的效用，相较于未套期保值前的效用值，套期保值后效用值增长率越高的投资组合，套期保值绩效越好.通常使用的效用函数为

其中，Φ为风险厌恶系数，根据投资者的不同而有所变化.套期保值绩效为

(9)

其中，U1表示未套期保值前的效用，U2表示套期保值后的效用，分母的绝对值符号是防止效用值为负使绩效的表示失去意义.由于效用越大越好，E2值越大表示套期保值后的效用增长率越大，套期保值绩效越好.

2 实证分析

2.1 数据样本

本文对辽宁农产品期货套期保值绩效进行分析，选择在大连商品交易所上市的大豆、豆粕、鸡蛋、玉米4种农产品，样本数据为农产品现货与期货的每日价格，分别为来自Wind金融终端的现货报价和大商所历史期货合约的每日收盘价；数据区间为2013年11月8日至2019年10月30日，每种农产品期货、现货价格分别包含1 429个数据.数据的选择方面：首先，期货合约是有多个同时在市场上交易的，我们选取的是对应时期活跃合约的价格；其次，由于现货市场每天都在交易，而期货市场则是根据交易所的交易时间进行交易，所以为了研究方便，在选取数据时剔除了期货价格与现货价格不能对应的数据.使用Eviews 10软件进行数据处理及分析.

2.2 单位根检验与协整检验

2.2.1 单位根检验 单位根检验的目的是检验序列是否为平稳序列，如果序列不平稳的话，进行回归分析时可能会存在伪回归.同时，单位根检验又是协整检验的前提，即两个序列为同阶单整序列时才可以继续分析协整关系.对8组数据的单位根检验结果如表1所示.

从表1可以看出，鸡蛋现货价格的原始序列的ADF检验统计量大于1%临界值小于5%临界值，所以此变量在5%的水平拒绝存在单位根的假设，但在1%的水平不能拒绝存在单位根的假设.鸡蛋期货价格的原始序列的ADF检验统计量大于5%临界值，小于10%临界值，所以在10%的水平拒绝其存在单位根的假设，但在5%的水平不能拒绝存在单位根的假设.剩余变量的原始序列ADF检测统计量均大于10%的临界值，所以均在10%的水平不能拒绝存在单位根的假设.而每一个变量的一阶差分序列的ADF检测统计量均小于1%临界值，即均在1%的水平拒绝存在单位根的假设.于是，在1%的显著性水平下，所有变量的原始序列均为非平稳序列，而经过一次差分之后均能达到平稳，所以各个变量均为1阶单整序列，记为I(1).

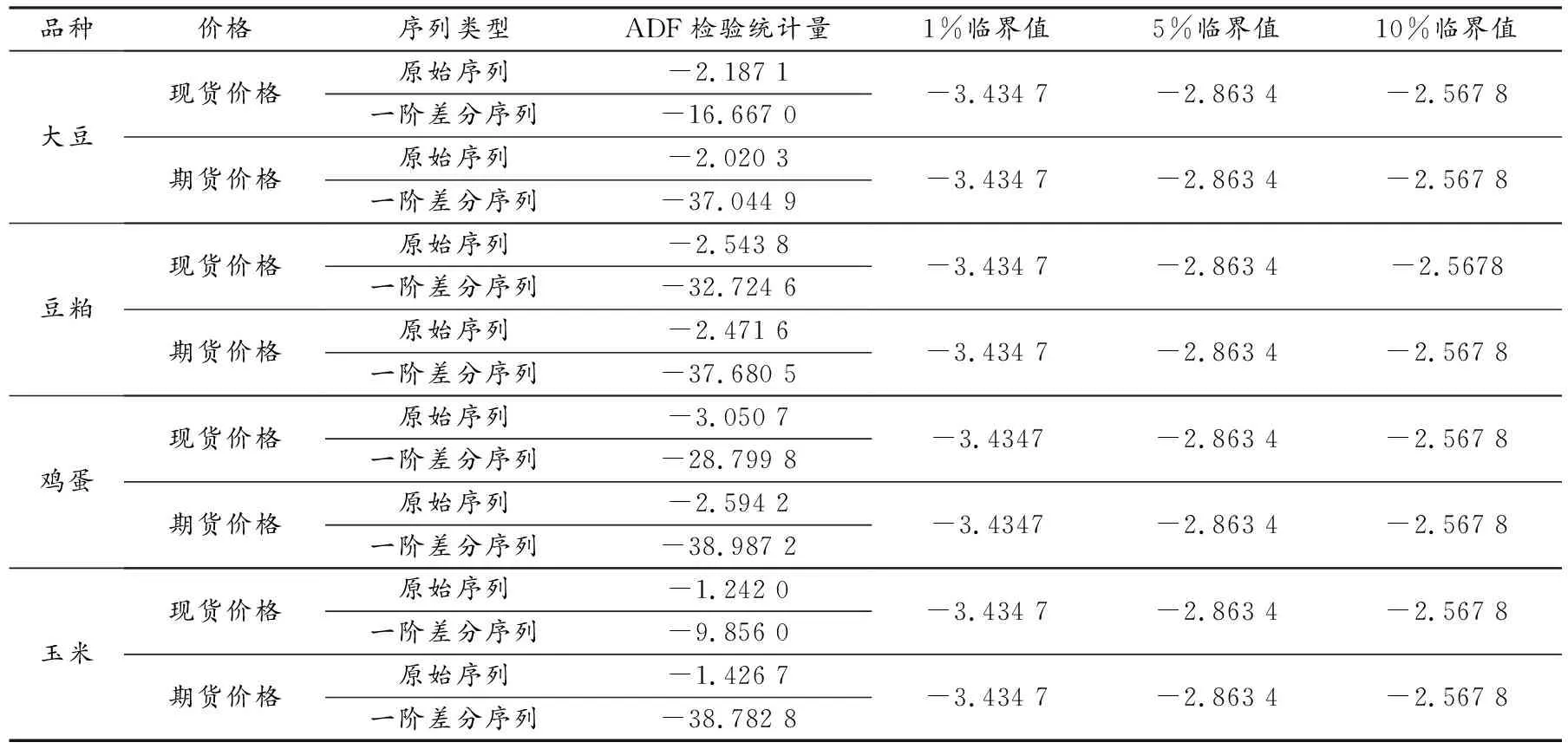
表1 4种农产品现货价格与期货价格单位根检验结果

2.2.2 协整检验 对于非平稳序列之间的关系，如果盲目回归，可能会出现伪回归.协整理论说明，即使两个变量是非平稳的，他们之间的线性组合也可能是平稳的，这为非平稳序列的建模提供了途径.为了检验各个品种的现货价格与期货价格之间的协整关系，采用EG两步法：第一步，判断两个变量是否为同阶单整；第二步，判断两个变量之间进行普通最小二乘回归后的残差序列是否平稳，若平稳，则两个变量具有协整关系.通过上文对单位根的检验，各品种的现货价格与期货价格均为一阶单整序列，则EG两步法的第一步通过.下面，对各品种期货价格与现货价格进行回归分析，并将残差序列进行单位根检验，结果如表2所示.

表2 4种农产品残差序列单位根检验结果

从表2可以看出，大豆、豆粕、鸡蛋3个品种，残差序列在1%的水平拒绝有单位根的假设，玉米的残差序列在10%的水平拒绝有单位根的假设.可以得出结论，这4个品种的残差序列在10%的水平是平稳的，说明他们的期货价格与现货价格是有协整关系的.

2.3 最优套期保值比率计算结果

利用Eviews统计软件对4种农产品按照上文所述的公式(1)～(7)分别进行回归分析，得到了各个模型下每种农产品的最优套期保值比率，如表3所示.

表3 4种农产品最优套期保值比率

从表3可以看出，整体上，豆粕的最优套期保值比率最高，其次为鸡蛋，然后是大豆，玉米的最优套期保值比率为负，这意味着一单位的豆粕现货进行套期保值，如果想要达到最优套期保值效果，需要的豆粕期货数量比鸡蛋和大豆都要多；而对于负的最优套期保值比率意味着如果想达到最优的套期保值效果，需要和上文中的买入套期保值策略和卖出套期保值策略相反才可以实现.极端地讲，如果最优套期保值比率为零，意味着只需要现货，就可以实现价格变动的方差最小，此时，向投资组合中加入任意数量的期货合约，都会增加组合的风险，意味着期货市场的规避价格风险作用为零，即不能给现货市场提供风险对冲功能；而负值的最优套期保值比率，则可以采用反向操作的方式来规避价格风险，所以期货市场的价格风险规避功能是按照最优套期保值比率的绝对值大小判断的.于是，按照豆粕、鸡蛋、玉米、大豆的顺序，这4种农产品的期货市场在回避价格风险的功能上是逐渐变差的.

2.4 套期保值绩效计算结果

2.4.1 “风险最小化” 根据上文中提到的方法，建立Ut和Qt两个序列，分别对其求方差，使用公式(8)分别对各个品种的套期保值绩效进行计算，得到结果如表4所示.

表4 “风险最小化”下套期保值绩效

从上文分析得到结论：此绩效值越大证明套期保值绩效越好.现使用表4中的数据，首先，对4种农产品分别进行分析：4种农产品得到的绩效值均为正，说明对于这4种农产品来说，4种模型计算出的最优套期保值比率均可以起到降低投资风险的作用.其次，4种农产品均是采用OLS模型时得到的套期保值绩效值最大；而绩效值最小的没有共性，大豆的是ECM模型，豆粕和鸡蛋是GARCH模型，而玉米则是B-VAR模型.但除了大豆外，其他每一个品种的ECM模型的绩效值均优于GARCH模型的绩效值.以上结果说明，OLS模型在对期货最优套期保值比率的估计上是最优的模型.最后，若将4种农产品的绩效最好的模型绩效值放在一起比较，可以排出从大到小的顺序为：豆粕、鸡蛋、玉米、大豆，这也证明了这4种农产品期货合约的回避价格风险功能是按照这个顺序逐渐变差的.

2.4.2 “效用最大化” 根据上文提到的方法，建立Ut和Qt两个序列，使用公式(9)分别对4个品种的套期保值绩效进行计算，得到结果如表5所示.

表5 “效用最大化”下套期保值绩效

对于投资者而言，为了套期保值而建立的资产组合的效用值越大越好.使用表5的数据进行分析：对每一个品种来说，每一种模型在每一个风险厌恶系数下得到的绩效值均为正；对每一个品种的每一个风险厌恶系数而言，OLS模型的绩效值均为最大值；除了大豆以外，其他3个品种的各个风险厌恶系数下，ECM模型的效用都比GARCH模型的效用大.上述结果说明套期保值在每一种情况下都是有效的，且使用OLS模型对最优套期保值比率的估计是最优的.对4个品种进行综合分析发现，将每一个品种的各个风险值下的最大绩效值放在一起比较，可以看出对每一个风险厌恶系数，绩效值大小均按照豆粕、鸡蛋、大豆、玉米的顺序递减，说明按照这个顺序，各个品种的期货合约对价格风险的回避能力逐渐变差.

3 结论与建议

3.1 研究结论

本文对大豆、豆粕、鸡蛋、玉米4种农产品的期货、现货价格变动使用了OLS、B-VAR、ECM、GARCH模型进行回归，估计出最优的套期保值比率，并对不同品种、不同模型所得到的套期保值比率使用了两种绩效评价方法进行计算，分别为“风险最小化”方法和“效用最大化”方法，得出以下结论：

第一，通过对4种农产品的现货价格和期货价格进行单位根检验，在1%的显著性水平，现货价格、期货价格序列均为非平稳序列，而一阶差分序列均为平稳序列.由此可知，4种农产品的现货价格与期货价格均为一阶单整序列，并不能简单地进行回归分析.价格序列不平稳的原因在于农产品的现货市场与期货市场都存在季节性、周期性或政策上、气候上的随机突变，这些因素会使价格进行非对称调整.

第二，在4种农产品的现货价格序列与期货价格序列均为一阶单整的条件下进行协整检验，可以得到4种农产品的现货价格与期货价格均存在着协整关系，表明存在着长期稳定的均衡关系.在期货市场上进行套期保值的农户及涉农企业可以关注现货市场与期货市场上的价格水平以及变动情况，对价格的未来走势有一个基本的把控.

第三，通过比较4种农产品的套期保值前绩效与使用各个方法进行套保后的绩效，可以发现每一个套保后绩效都优于未套期保值的绩效.说明使用辽宁农产品期货进行套期保值是有规避价格风险作用的.

第四，根据4种农产品的4种模型分别计算出来的最优套期保值比率以及绩效可以得知，OLS模型比起其他3种模型，套期保值绩效更好.因此，在期货市场上进行套期保值的农户及涉农企业可以按照OLS模型的方法计算最优套期保值比率，从而进行套期保值操作.

第五，虽然使用GARCH模型进行套期保值比率在实证分析中表现不好，但是根据其原理可知，GARCH模型适合波动较大的市场环境，可以根据市场情况计算出时变的最优套期保值比率，从而不断进行仓位调整，适应市场的波动.

第六，通过比较4种农产品的套期保值绩效可以看出，4种农产品的期货合约，回避价格风险能力排名靠前的按强弱顺序分别是：豆粕和鸡蛋，而大豆与玉米使用两种评价方法得到的排序不同，但均为后两名.在使用“风险最小化”方法时，得到的绩效值即为套期保值可以降低的风险大小，最多的豆粕约为24%，排名第二的鸡蛋约为10%，其他2种农产品均不超过5%.所以在期货市场上进行套期保值交易时，对于交易品种可以有所选择的投机者来说，尽量选择豆粕或鸡蛋，这样可以提高套期保值的风险规避能力.

3.2 政策性建议

通过实证研究可以发现，辽宁农产品期货市场的规避价格风险功能并未得到充分发挥，所选农产品中最优的也仅能规避24%左右的风险，其余大部分还在5%以下的水平.期货工具套期保值绩效过低，对于农户及涉农企业进行规避风险产生的意义并不大.就此，本文提出如下建议：

第一，对农户及涉农企业来说，虽然目前的期货市场活跃度不足导致使用期货套期保值规避价格风险的效果不好，但使用期货套保优于不使用期货.在选择模型进行估计套期保值比率时，选择OLS模型能使套期保值绩效最大化.

第二，应当加大对期货产品的宣传，使农户及涉农企业了解更多的期货知识，进而提高其参与期货市场的积极性.农产品期货市场，农户是主要的参与主体之一，在农户受教育程度普遍偏低的背景下，其参与期货市场进行套期保值的意识必然相应偏低.如果充分进行期货知识的宣传，增加参与期货交易的农户数量，不仅农户本身可以通过套期保值降低风险，而且会使整个期货市场的活力增加，进而增强期货市场整体规避风险的能力，使套期保值绩效提升，形成良性循环.

第三，适量增加农产品期货品种，扩大市场规模.由于期货具有保证金制度，所以在投资时相当于有一定的杠杆率，这在金融市场中是十分具有吸引力的特征.如果增加农产品期货品种，则可以使投资者在期货市场中的选择面变广，扩大了市场的规模，进而增强期货市场的流动性，加强期货规避价值风险的功能，提升套期保值绩效.