Meteodyn WT软件的大气热稳定度影响研究

袁红亮，王 炎，陈 彬，宋俊博

(中国电建集团西北勘测设计研究院有限公司,西安 710065)

0 前 言

在碳达峰碳中和的背景下，风电作为新能源产业中的重要一环，对实现“30·60”战略目标将发挥重要的作用。风能资源评估在风电开发过程中起着关键的作用，随着风电开发建设的进度逐渐加快，各种风能资源评估软件应运而生，软件根据用户输入的地形、大气热稳定度、粗糙度等参数进行边界条件的生成，继而进行风电场流场模拟[1]。其中，大气热稳定度在风能资源评估中是非常重要的参数，不同的大气热稳定度代表不同的大气层结特性，其取值不同会导致不同的流场模拟结果，继而影响风能资源评估的准确性。为了研究大气热稳定度对风能资源评估的影响，多位学者对其进行了相关研究。Gualtieri详细分析了荷兰Cabauw地区10、20、40、80 m测风塔的大气热稳定性与风切变指数的时间变化关系[2]。研究发现，相对于对数定律，幂定在不稳定和中性层结条件下给出更接近实际的风廓线[3-5]。然而，目前基于Meteodyn WT软件进行大气热稳定度的设置及其影响研究较少。在实际工程计算中，风电场大气热稳定度应根据工程实际情况进行取值。一般情况下，工程师都采用软件默认的值，这种大气热稳定度取值方法虽然简便，但无法反映场风电工程的真实情况，也无法保证计算的精确性。

本文以某风电场工程为例，研究Meteodyn WT软件中不同大气热稳定度取值对风速、风切变指数及风廓线的影响，提出大气热稳定度取值的相关方法及建议，为风电工程中合理地对大气热稳定度进行取值提供参考。

1 Meteodyn WT软件和大气热稳定度简介

Meteodyn WT软件是法国美迪公司专门为解决大气边界层问题而设计的软件，采用计算流体力学的方法(CFD)进行空间风流模拟，在限定边界条件下，数值求解三维雷诺平均纳维—斯托克斯(RANS)方程，并应用适合的湍流模型对目标区域的风流特性参数进行求解计算[6-7]，得到整个场区的风流情况，可用于风能资源评估与发电量计算。该软件减少了复杂地形条件下计算的不确定性，因此对于复杂地形风电场的风能资源评估具有较好的适用性[8]，同时也适用于平坦地形风电场。

Meteodyn WT软件中的大气热稳定度通过Obukhov长度来定义，该长度可以反映机械性湍流与热力效应产生的浮力湍流之间的相对主导性。Meteodyn WT软件的CFD计算中共有 10 个不同的大气热稳定度等级可以选择。大气热稳定度等级从 0(非常不稳定)至 9(强稳定)稳定度逐渐提高。表1列出了不同热稳定度等级下对应的 Obukhov 长度。

Meteodyn WT软件中大气热稳定度对入口风廓线的影响见图1 。从图1中可以看出，大气越稳定，入口风切变越大；同时场区内的风切变也越大。

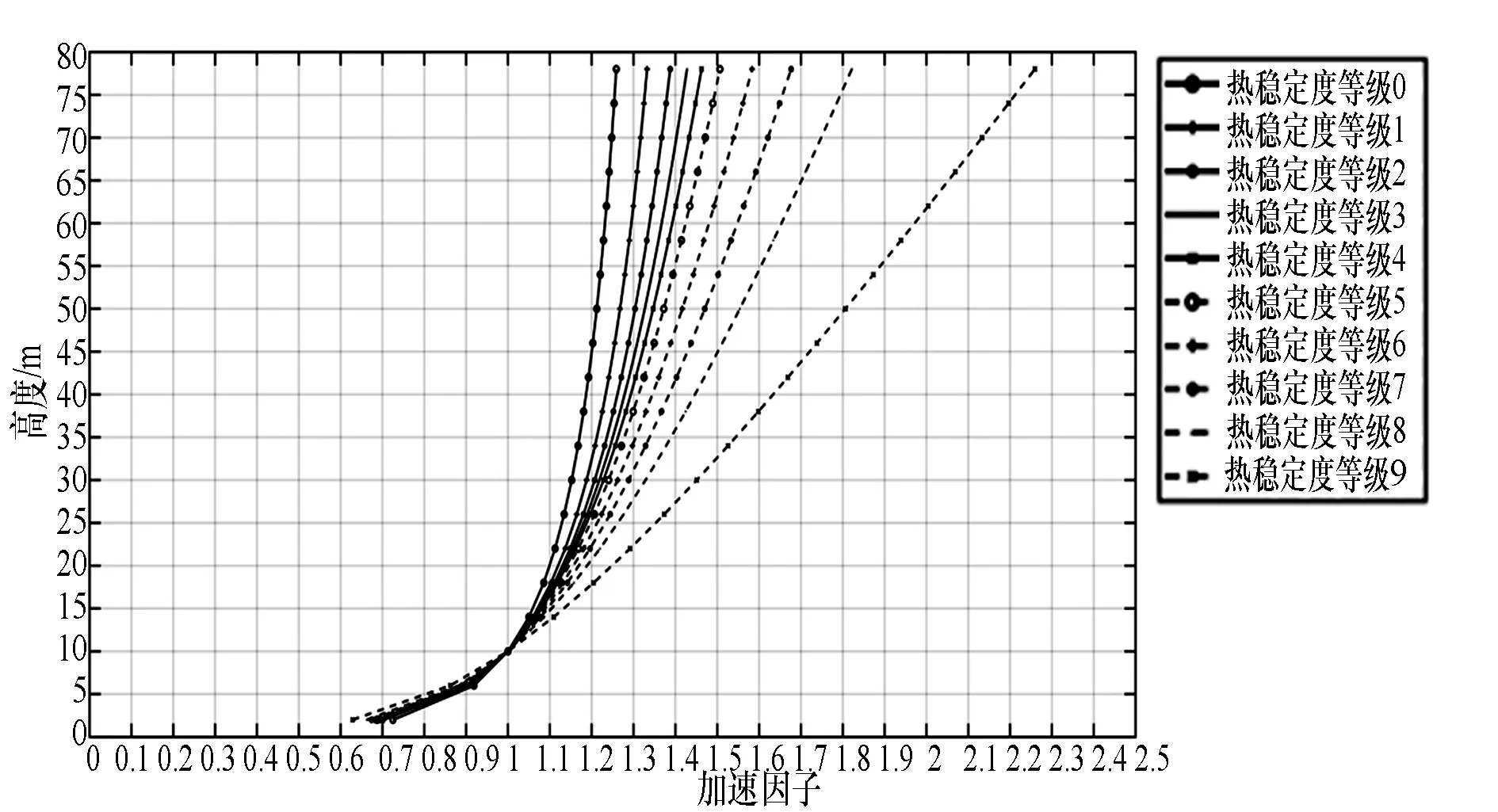
图1 不同的热稳定度条件下的入口风廓线

2 算例概况

本文选取的某风电场为我国中原地区平坦风电场，地表主要为农田和村庄。风电场内共有3座测风塔，分别为01、02、03号。3座测风塔高度均为100 m高，风速观测高度均为100(1)、100(2)、80、60、40、10 m，风向观测高度均为100、80、10 m。风电场的主风向以北风、南风和南西南风为主。测风塔位置如图2所示。

图2 某风电场测风塔位置

为了比较不同大气热稳定度取值下测风塔互相推算模拟的准确性，本文选取3座测风塔同期时段为2016年1月1日至2016年12月31日的100 m高度测风数据。

3 计算方案

选用实测1∶2000 数字化地形图，通过 Meteodyn WT 软件对真实地形建模。在3座测风塔代表年实测数据、功率曲线、粗糙度等其它输入参数确定的前提下，大气热稳定度是影响风能资源评估的关键因素。本文研究方法是在保证其它参数一致的情况下，改变Meteodyn WT软件中大气热稳定度的取值，以此分析大气热稳定度对风速、风切变指数及风廓线的影响。具体步奏如下：

第1步,初始建模。根据实测测风数据和场区实测1∶2000地形图，利用 Meteodyn WT 软件模拟场区内的风能资源分布情况。初始模型定向计算相关参数设置为：最小水平分辨率为60 m，最小垂直分辨率为5 m，热稳定度等级初步选择2(中性)，粗糙度直接引用Meteodyn WT软件内置的地理信息数据库，风向扇区间隔为 22.5°。按照上述参数设置进行CFD定向计算直至收敛。

第2步，模型检验。采用03号测风塔作为参考塔对初始模型进行检验。根据03号测风塔数据进行综合计算，将Meteodyn WT 综合计算结果发送至 Windographer FMV，对03号测风塔位置处的模拟风廓线和实测风廓线进行对比分析，以检验初始模型对实际风场的拟合是否符合。初始建模得到的参考塔模拟风廓线与实测风廓线的对比见图3。可以看出，风廓线模拟效果并不好。另外，根据参考塔全风向平均实测风切变指数为0.362，而初始模型模拟的全风向平均风切变指数为0.160，该初始模型经检验明显与实际风场有较大偏差。

图3 初始模型中 03号模拟风廓线与实测风廓线对比大气热稳定度

第3步，模型校正。针对初始模型与实际风场不符的情况，可以考虑调整的影响风廓线及风切变的参数有：地形精度、地表粗糙度、森林模型、大气热稳定度。本文在保证地形精度、地表粗糙度、森林模型等其它参数与风场实际相符的条件下，只调整大气热稳定度的取值，以此分析大气热稳定度的影响。

在此提出风切变校正法对大气热稳定度进行调整，以使校正后的模拟结果更接近风场实际。大气热稳定度的风切变校正法参考塔位置处的全风向平均模拟风切变指数、模拟风廓线与实测值不符时，改变大气热稳定度的取值重新进行模型综合计算，直至模拟风切变指数与实测风切变指数接近，误差较小(根据工程经验误差绝对值小于0.04)；且模拟风廓线与实测风廓线较为相符，则认为该取值对应的大气热稳定度为最终值，能最大程度反应风场实际。

针对算例，本文初拟8种计算方案，对模型进行校正，采用风切变校正法来确定算例中大气热稳定度的取值。具体计算方案见表2。

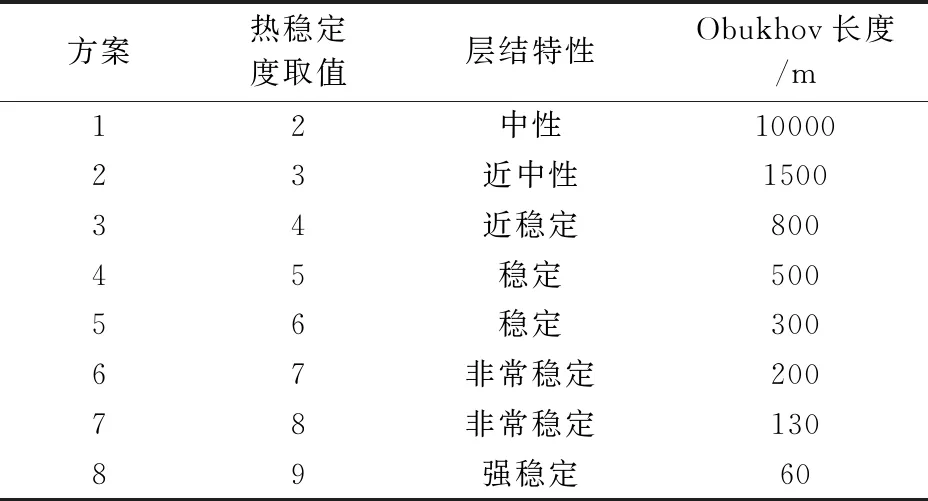
表2 大气热稳定度计算方案

4 计算结果

将算例风场内的其中一座测风塔作为参考塔，利用其100 m高度实测数据对其它2座测风塔位置处100 m高度的风速、风切变指数和风廓线进行模拟，然后与实测风速、实测风切变指数(不考虑10 m高度)、风廓线进行对比，对3座测风塔模拟的风速、风切变指数误差取绝对值后进行平均，得到8种计算方案的模拟误差结果见表3、图4～5。

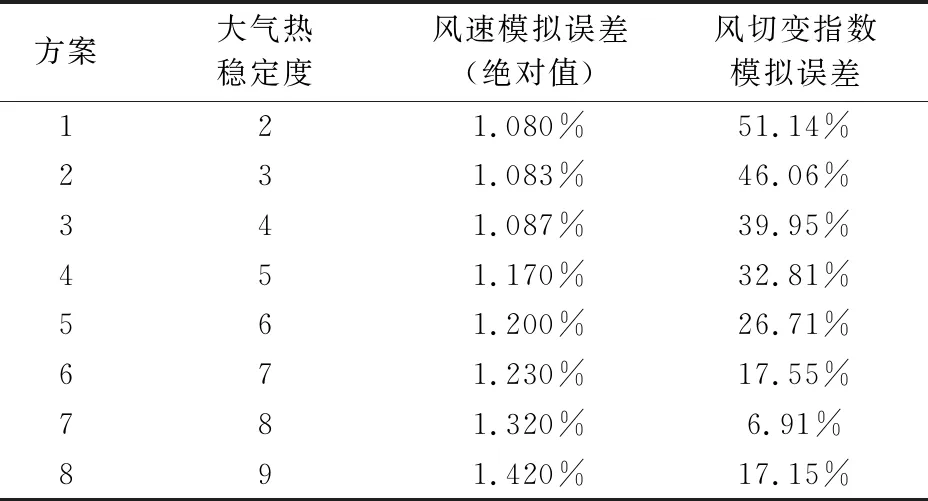
表3 各方案风速、风切变指数模拟误差表

由上述模拟误差图表可以看出：

(1) 随着大气热稳定度的增大，模拟的风速误差不断增大，其中最大值为1.420%，最小值为1.080%。

(2) 风切变指数模拟误差在热稳定度为8时最小。之后随着热稳定度的减小，风切变指数模拟误差增大。

图5 不同大气热稳定度风切变指数模拟误差

(3) 热稳定为2时，模拟的100 m高度风速误差相对最小，但风切变指数模拟误差较大，风廓线拟合较差，说明此时模型只在100 m高度的平面上具有一定的精度，在垂直方向上与实际风场相差较大，风廓线拟合效果较差。

(4) 综合上述成果，采用风切变校正法，综合考虑风速、风切变指数模拟误差结果，算例中大气热稳定度取值应为8。

各测风塔的风速、风切变指数模结果见表4和表5。可以看出，风速模拟的误差在0.00%～2.23%之间，误差绝对值平均为1.32%，模拟结果精度较高，误差较小；风切变指数模拟误差绝对值在0.001～0.035，风切变误差最小。

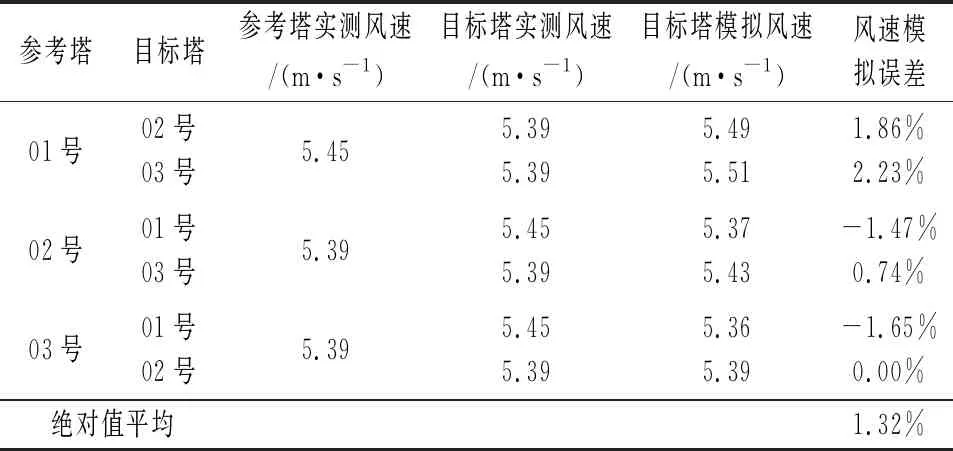
表4 大气热稳定度取8时各测风塔风速模拟结果

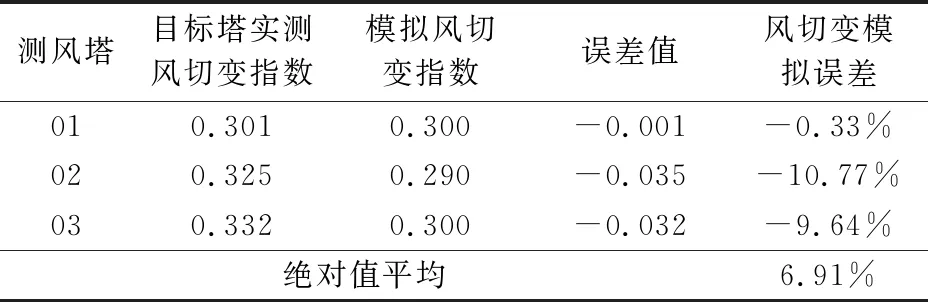
表5 大气热稳定度取8时各测风塔风速模拟结果

03号测风塔风廓线模拟结果见图6。可以看出，风廓线拟合结果较初始模型(图3)有了很大改善，由此可认为经风切变校正法校正后的模型与实际风场符合。

图6 03号测风塔的模拟风廓线与实测风廓线对比(大气热稳定度取8)

5 结 论

通过对Meteodyn WT中大气热稳定度取不同值对算例的模拟结果进行分析，评估了大气热稳定度对风速、风切变指数、风廓线的影响。并提出了风切变校正法，用来确定大气热稳定度的最终取值，形成结论如下：

(1) 算例中，当热稳定度为8时(非常稳定)，风速模拟的误差在0.00%～2.23%，误差绝对值平均为1.32%，模拟结果精度较高；风切变指数模拟误差绝对值在0.001～0.035，风切变误差最小。且风廓线拟合较好，模型与实际风场较为符合。

(2) 中原地区的平坦风电场，地表主要为农田和村庄的条件下，随着大气热稳定度的增大，模拟的风速误差不断增大，但模拟的风切变指数误差不断减小。

(3) 实际工程中，可采用风切变校正法对大气热稳定度进行调整，可使校正后的模拟结果误差更小。

(4) 大气热稳定度的最终取值，应结合风切变校正法和风廓线模拟的符合度综合确定。