基于SVM算法的红层公路边坡稳定性快速评价方法
张 硕,郑 达,张 文
(1.成都理工大学环境与土木工程学院,成都 610059;2.中国地质科学院探矿工艺研究所,成都 611734)
0 前 言
红层主要是指中生代和新生代挽近系的湖相、河湖交替相或是山麓洪积相等陆相碎屑岩,以粉细砂岩、泥岩和页岩为主,主要分布在中国西南、西北、华东、中南、华北、东北地区,其中又以西南地区四川盆地及盆地边缘、西昌-滇中地区、滇西地区分布较为广泛。随着交通强国与“一带一路”战略的提出,我国西部地区逐渐浮现出一张规模庞大的高速公路网,而此地区公路工程的修建不可避免地要穿越红层山区。由于红层软岩具有胶结程度差,强度较低、易风化、水理性差、变形大的特点,加之红层斜坡岩体内不同程度发育有层间错动带、泥化层等软弱夹层,导致其变形失稳模式复杂[1],例如通常情况下稳定性较好的平缓岩层地区,却常常在岩层倾角不超过10°,有时甚至反倾3°~5°的岩层中发生大型滑坡[2];天然状况下难以发生滑坡的缓倾角岩质边坡,在强降雨条件下,却屡见大规模群发性滑坡灾害[3];或是边坡在自然情况下稳定性良好,却在开挖后迅速产生变形滑移[4],由此可见这类滑坡具有扰动或降雨后成灾速度快、识别难度大、成因机制复杂、成灾模式独特、隐蔽性强、减灾防灾难度大的特点。因此,建立公路地区红层边坡快速评价体系对红层公路边坡的防灾减灾工作具有重要意义。
据统计截止2020年底,四川省内正在运营的高速公路约有52条,其中约有30条都处于红层地区[5],占比约57%,在红层地区公路修筑过程中常常发生各种地质灾害问题,如正在修建的仁沐新高速公路,因施工中的边坡开挖扰动,诱发了大量的工程滑坡与古滑坡复活(见图1)[6],不仅对相关区域人民生命财产安全构成严重威胁,而且会对重大工程建设与运营造成巨大影响。

图1 开挖边坡局部失稳
公路施工通常采用全线多个标段同时施工,这样势必会在短期内出现数量众多的开挖边坡,而很多红层边坡在开挖过程中或者开挖后不久就会发生岩体变形、局部崩塌与顺层滑坡等地质灾害,严重影响工程安全与施工进度。目前对公路开挖边坡稳定性的快速评价方法主要有3种:
(1) 采用传统的定性分析结合强度理论的边坡稳定性评价方法对公路边坡进行评价。此方法需要丰富的工程经验,在对每个边坡进行地质模型建立工作后,进行定量评价,但工作量巨大,难以在短时间内完成评价,不适合在线性工程边坡中应用[7-8]。
(2) 基于岩体强度分级RMR法的快速评价方法。通过分析影响边坡稳定的众多因素,从中选取合理的特征对边坡进行定性或半定量的稳定性评价,该方法评价结果的合理性受各种修正系数的限制,且各因素分级标准的选取及权重确定方面多具主观性[9-12]。
(3) 建立评价指标体系。通过数量化理论或者运用机器学习理论进行边坡稳定性分级的快速评价方法。相比之下,该方法是目前最快速、效率最高的方法[13-15]。
随着当前机器学习(Machine Learning)理论的发展,为各种实际难题提供了很好的解决方案。边坡稳定性评价可看作是一个分类问题,且影响因素与边坡稳定性之间是非线性关系,而SVM算法能很好解决维度高、非线性强、样本小的分类问题。本文通过机器学习理论与SVM算法对边坡的评价指标与稳定性等级进行分析,找寻二者之间的非线性关系,分析红层边坡的评价指标数据,建立模型预测边坡的稳定性等级,尝试形成一套针对红层地区公路边坡稳定性的快速评价方法,为红层地区公路的施工与防治提供参考。
1 边坡稳定性快速评价指标
为了选取合理的边坡快速评价指标,笔者对典型红层公路边坡变形破坏模式进行了分析,发现边坡崩滑灾害的发生是众多影响因素共同作用的结果,总的来说可以分为两类:一是地质因素,即边坡所处的地质环境条件,是影响边坡天然条件下稳定程度的基本条件,如地形地貌、地层岩性、岩体结构面特征、坡体结构特征、水文地质条件等;二是诱发因素,如开挖、降雨与地震等。
边坡地形地貌特征主要包括坡高、坡宽、坡度等,与边坡失稳的易发程度和规模息息相关。岩性组合则是构成边坡的物质基础,决定边坡的物理力学性质,在很大程度上决定着开挖边坡的稳定与失稳机制。红层坡体内常发育泥化夹层、层间错动带与大量的构造节理与裂隙,其起伏程度、发育密度、接触状态、填充物特征对结构面的抗剪强度起到关键性控制作用。边坡坡体结构主要指结构面的产状、性质、空间位置等与坡面之间的关系,对边坡的稳定性起着控制型作用,对于红层边坡来说,坡体结构的差异决定了边坡变形位置、失稳模式、成因类型的不同。在红层地区,基岩裂隙系统是地下水入渗、运移和储存的主要空间,裂隙的规模、密度、张开度、连通性、透水性等因素决定了红层边坡的给水性和导水性,对红层滑坡的形成至关重要。
红层边坡破坏的诱发因素主要包括降雨与人工开挖等方面,其中降雨对边坡的影响主要体现在加速边坡岩体风化和崩解速度、增加坡体自重、软化岩土体形成垂直裂隙中的静水压力与底滑面扬压力。工程开挖则会改变自然边坡的几何特征与地质环境,是边坡失稳的重要诱发因素,在开挖过后临空面方向往往会发生大面积卸荷,导致大范围的扰动变形。
根据上述分析,本文选取反映边坡稳定性的10个快速评价指标(见图2),其中边坡的几何特征指标包括边坡坡高、坡宽、岩性与结构特征指标包括岩性组合特征、结构面特征、岩体结构类型、坡体结构类型、外部触发因素指标包括边坡开挖级数、开挖高度、平均开挖坡度、最大单日降雨量。这些指标都易于快速获取,它们相互作用组成红层公路边坡稳定性快速评价指标体系。

图2 红层公路边坡稳定性快速评价指标
2 边坡稳定性快速评价方法
边坡稳定性影响因素众多,常规的方法很难找到一个较好的关系式来描述边坡稳定性与影响因素之间的非线性映射关系。而SVM算法无论样本点是线性可分的、近似线性可分的,还是非线性可分的,都可以利用某些支持向量所构成的“超平面”将样本点以较高的准确度切割开来,适用于边坡稳定性的预测分类问题,本次研究基于机器学习全流程理论构建模型。
2.1 数据理解
评价方法的第一步是“数据理解”阶段,对建模数据进行描述性统计和可视化分析,从整体和局部两个方面去揭示数据内深层次的关系、结构与模式,进而定位到哪些方面可以去优化数据集质量,通常依据数据类型分别从单变量与双变量两方面进行分析。
2.2 数据预处理
评价方法的第二步是“数据预处理”阶段,是提高算法准确度的关键步骤。在机器学习中根据算法的特征和数据的特征对数据进行转换,主要内容如下:
(1) 数据清洗
数据清洗目的是为了提高数据采集质量。本次研究样本数据通过数据理解阶段的单变量分析与双变量分析,未发现存在重复数据、不一致值、缺失值,仅发现少数边坡样本出现离群值。出现离群值的原因及处理方法如表1所示。

表1 离散值出现原因及处理方法表
(2) 连续型变量无量纲化
数据集中的连续型数据变量分布跨度过大,需要进行数据尺度调整与标准化、归一化处理。
调整数据尺度:通常情况下数据的各个属性是按照不同的方式来度量数据的,那么通过调整数据的尺度使得数据所有属性的尺度变的统一,就会给机器学习的算法模型训练带来极大的方便。依次对训练集和测试集中的连续型数据进行数据尺度调整,将数据都聚集到0附近,方差为1。相同的数据尺度,能够提高与距离相关的算法的准确度。数据范围调整之后,所有数据点的特征数值都被限制在了规定的范围内。
归一化处理:为了优化之后所建立模型的收敛效果,对数据进行归一化处理,将每一行数据的距离处理成1,称为“归一元”处理,计算公式为:
(1)
公式(1)中:x为处理后的数据;xi为原始数据中第i个数据;xmin,xmax分别为原始数据中该类型变量的最小值与最大值。
归一元处理后不仅能提高数据的表现,而且还保留与原始数据变量相同的数值大小排序,这对部分使用权重输入或者使用距离输入的算法的性能提升十分有效。
(3) 分类型数据量化
目前机器学习算法及模型都只能接收数值类型的数据,但“岩性特征”“结构面充填特征”“岩体结构类型”“坡体结构”“最大单日降雨量区间”都是分类型数据,它们都来自一系列固定的可能取值,是离散的,而不是连续的,因此要对这些分类型数据进行量化。
表示分类型变量最常用的方法就是使用One-Hot编码,原理是将一个分类变量表示为一个或多个子特征,子特征取值为0和1。对于线性二分类的公式而言,0和1这两个值是有意义的,我们可以像这样对每个类别引入一个子特征,从而表示任意数量的类别。如果一个边坡的结构面充填特征取某个值,那么对应的特征取值为1,其他特征均取值为0。因此,对每个数据点来说,6个子特征中只有一个的取值为1(见表2)。

表2 数据特征值One-Hot数据处理表
(4) 降 维
样本中数据的种类越多,维度就越大,过多的维度会造成机器学习的“维灾难”,即模型建立及运行所需的时间与学习成本大大增加,性能也会随之降低,因此需要对高维度数据集展开降维处理。
模型输入的数据种类有坡高、坡宽、平均开挖坡度、开挖高度、开挖级数、岩性特征、坡体结构、岩体结构、结构面充填特征、最大单日降雨量,共10类。为进一步提高模型的性能,减少实际工作中数据采集时非必要工作量,将展开降维处理,至于应该精简哪几个特征,则需要特征选择。这里选用机器学习中常用的卡方检验方法来评估各个特征与稳定性之间的关联度,卡方检验得出的分数越高,说明该特征越重要,针对以上10个特征的检验结果如图3所示。
从图3中可知,坡宽与开挖级数是重要性最低的两种特征,将讨论其是否被剔除。首先是开挖级数,开挖级数与开挖高度存在较强的正相关性关系,这也说明开挖级数可以由开挖高度来代表参与稳定性评价,且开挖高度重要性相比开挖级数高出许多,因此决定剔除开挖级数特征。而坡宽重要性排名倒数第二位,同时却是开挖级数重要性数值的1.5倍,也与平均开挖坡度、岩性结构特征没有拉开差距,可以作为表征边坡规模的特征之一,现场数据易获得,因此,认为坡宽特征予以保留。经过讨论分析,决定精简开挖级数特征指标,保留其余9个指标进行机器学习模型的建立。

图3 卡方检验得分
2.3 建立快速评价模型
本次红层公路边坡稳定性快速评价方法SVM算法模型的实现采用基于Python语言平台下的Scikit-learn机器学习工具包中的SVM函数包,超参数搜索及交叉验证的实现同样采用Scikit-learn机器学习工具包中的GridSearchCV包。将原始数据集内样本进行划分,第一部分用来训练算法建立模型,第二部分则使用模型进行评价预测。
(1) 核函数选择
SVM算法中常用的核函数有线性核函数、多项式核函数与高斯核函数,核函数的选取是影响SVM算法优劣的重要因素,以上几类核函数中,线性核函数针对线性可分样本数据分类效果最理想,在非线性分类问题中不推荐使用;多项式核函数可以将样本数据映射到高维空间;高斯核函数参数较少,具有针对样本数据中噪声很强的抗干扰特性,局部拟合效果强大,能够使非线性样本数据样本映射到高维空间使之可分,是应用范围最为广泛的核函数。本次研究结合边坡变形稳定性问题复杂且非线性的特点,考虑到模型计算量与效率,拟选择高斯核函数作为本次研究评价模型的核函数。
(2) 超参数选择
SVM包涉及的重要超参数有:“C”、“gamma”,其中C是惩罚系数,为调节优化方向中两个指标(间隔大小,分类准确度)偏好的权重,C越高,说明越不能容忍出现误差;C越小,容易欠拟合;C过大或过小,泛化能力均会变差。gamma是高斯函数自带的一个参数,隐含地决定了数据映射到新的特征空间后的分布,gamma值越大,支持向量越少;gamma值越小,支持向量越多,支持向量的个数影响训练与预测的速度。
采用网格搜索法来进行参数寻优,选取C,gamma的初始搜索界限定为(10-3,103),步长为10的等幂,在搜索的最佳参数附近减小步长继续搜索,惩罚因子C不能过大或者过小,通常情况下不会超过设置的搜索范围。
最终利用网格搜索法得出了模型建立的最佳参数组合:C=10,gamma=100,图4为网格搜索法参数寻优过程中的适应度值变化趋势。
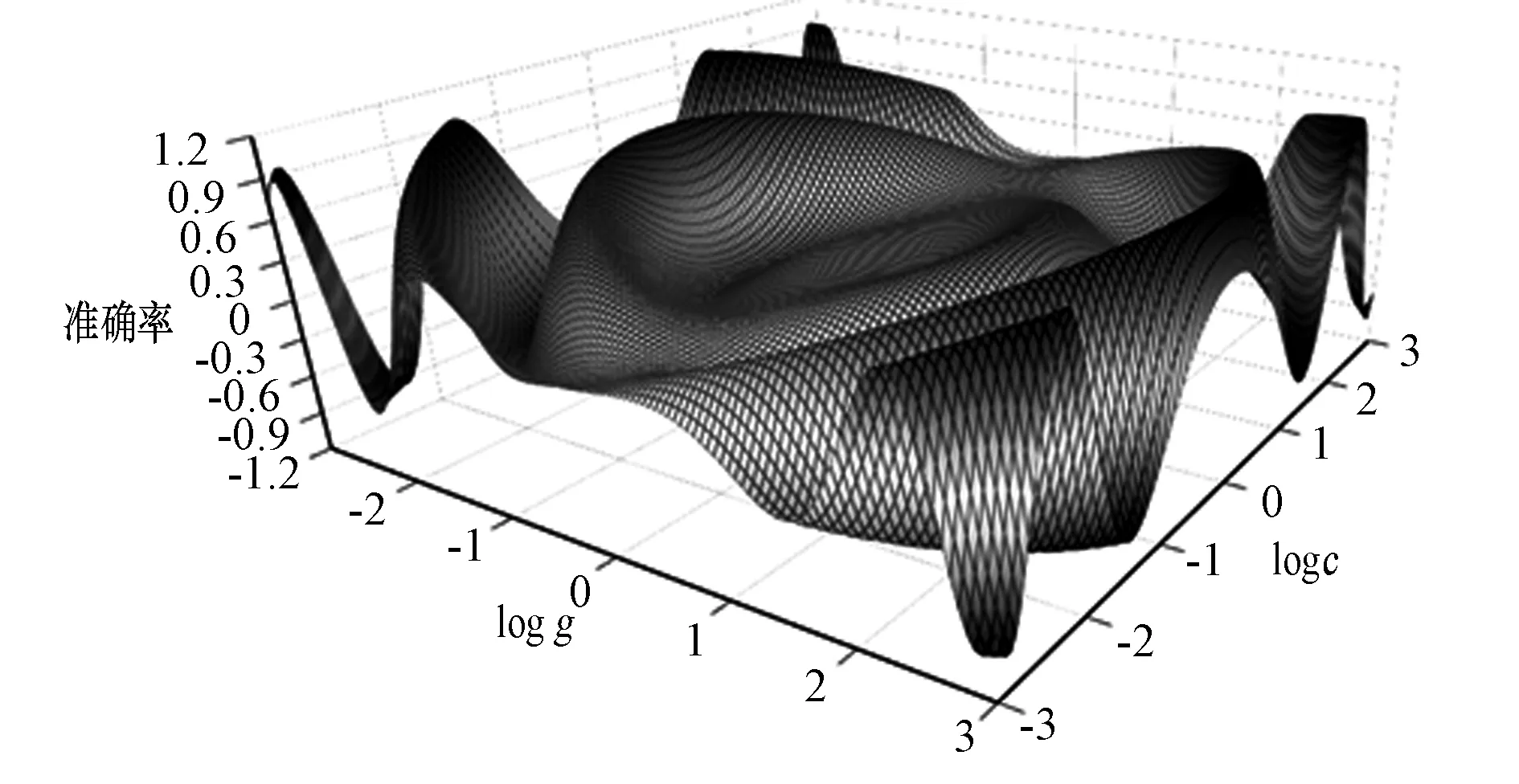
图4 网格搜索法搜索SVC参数
(3) 模型训练
SVM模型训练过程是基于所选取多次方的多项式核函数,将样本数据点投射到高维的样本特征空间中。通过SVM算法找寻到各个分类特征数据与其他特征数据之间的最优分类平面,获得表征各分类特征的支持向量集与其相对应的VC可信度,最终生成可评价各样本类别的判别函数。
SVM判决过程是将样本的特征信息由核函数映射到特征空间内,作为SVM模型训练出的判别函数的输入源,通过边坡评级分类判别函数得出分类结果,建立支持向量机算法中用于分类的SVC(Support Vector Classification)模型,模型训练过程如图5所示。
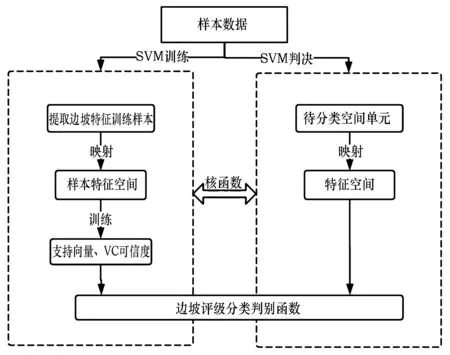
图5 模型构建流程
使用建立的模型对训练集与测试集样本展开评价,经过测试发现训练集35个样本预测正确31个,准确率88%;测试集15个样本预测正确14个,准确率93.3%,预测错误的样本稳定性等级为“较差”,被误分类到稳定性“差”类别,虽然个别样本评价结果与实际不一致,但是对于整个模型来说,准确率依然较高,由此认为该模型分类效果很好,有很强的泛化能力。
(4) 模型性能评估
对于分类型模型,不仅要关注其预测准确度怎样,还需要检查模型的命中率(边坡样本中实际稳定性差却被预测为好的样本所占的比率)和假警报率(边坡样本中实际稳定性好却被预测为差的样本所占的比率)这两个指标,并通过这两个指标绘制ROC曲线来评估模型。AUC表示ROC曲线下的面积,AUC值就是处于ROC曲线下方的那部分面积的大小。通常AUC的值越大,诊断准确性越高,AUC值评价模型预测是否准确的标准如表3所示。

表3 AUC评价标准
训练完成后模型输出的ROC特征曲线如图6所示,显示该模型的AUC为0.823,根据AUC评价标准,模型结果在0.7~0.9,表明模型的分类效果较好,预测准确程度较高,能较好地评价边坡的稳定性等级。

图6 SVM算法的ROC曲线
(5) 多种机器学习算法精度比较
根据选取的边坡样本数据集的特点,建模时选择了在处理样本少、维数高、非线性、离散值少情况下具有优势的支持向量机(SVM)算法。为了检验SVM算法是否是解决本类问题最合适的算法,特意选择了目前使用较多的4种算法来对比,分别是线性判别分析(LDA)、逻辑回归算法(Logistic)、k近邻分类算法(Knn)与朴素贝叶斯算法(Naïve Bayes),采用相同的数据,参数选择、性能评估时与SVM算法一致,用训练集数据来进行建模之后,再用各个模型分别对训练集与测试集样本进行预测评估,比较结果如表3所示。
从表4中可以看出,支持向量机算法在训练集和测试集分数排名均为第一,证明针对本次研究的问题和建模数据,选择SVM算法是最合适的。

表4 不同算法的性能比较
3 工程实例验证
以上研究完成了基于SVM算法的红层公路开挖边坡稳定性快速评价方法构建,为了检验该方法的性能,选取工程实例进行验证。
3.1 工程实例
四川省仁沐新高速公路起于眉山市仁寿县止于宜宾市屏山县新市镇,全长201.8 km(其中主线全长158.029 km,马边支线全长43.8 km),全线开挖边坡400余处,穿越的地形地貌单元复杂,丘陵、谷地、山地以及高原前缘地貌皆有涉及,沿线出露的地层主要有中侏罗纪系上统沙溪庙组、中统遂宁组、蓬莱镇组、遂宁组等红层地层以及第四系冲洪积、坡残积、崩坡积等堆积物。
研究区域林木茂盛,侵蚀构造地貌较为发育。边坡最多开挖级数达到了7级,开挖高度最高有70 m,由于施工开挖退坡深度小,且边坡坡度较陡,导致开挖面附近岩体风化程度较高,因此在一定情况下这些边坡的稳定性不足,容易失稳变形。筛选仁沐新高速公路主线边坡数据,选取其中16个边坡(见表5),从其原始边坡勘察研究报告中提取相应指标数据来进行红层公路开挖边坡稳定性快速评价的应用验证工作。

表5 仁沐新高速公路典型边坡评价指标
3.2 评价结果分析
将表5中各个边坡的指标数据按评价方法进行计算,得出相应的预测结果如表6所示。计算结果与现场边坡稳定性的地质定性判断的吻合率接近95%,说明采用上述指标进行红层开挖边坡的快速评价是可行的,其评价结果对实际工程具有一定的参考价值。

表6 仁沐新高速公路边坡稳定性快速评价结果
4 结 论
本文以红层地区公路边坡稳定性快速评价为研究目的,分析了影响红层边坡稳定性的因素,进一步以机器学习理论为基础,建立了基于SVM算法的红层公路边坡稳定性快速评价模型,以仁沐新高速公路主线边坡为例验证模型的性能,得到以下结论:
(1) 建立红层公路边坡稳定性快速评价指标体系,选取反映边坡稳定性的10个快速评价指标,其中边坡的几何特征指标包括边坡坡高、坡宽,岩性与结构特征指标包括岩性组合特征、结构面特征、岩体结构类型、坡体结构类型,外部触发因素指标包括边坡开挖级数、开挖高度、平均开挖坡度、最大单日降雨量。
(2) 运用机器学习理论,建立以SVM算法为核心的红层公路边坡稳定性快速评价模型。利用单变量分析与多变量分析来获得建模数据的特征,采用数据清洗、连续变量无量纲化、分类型数据量化、降维等操作展开预处理研究,以提高数据集质量,选取与数据特征相匹配的SVM(支持向量机)算法与高斯核函数建立模型,通过网格搜索法得出了参数C和gamma的最佳组合,由此构建了训练模型。为突出支持向量机算法对边坡稳定性快速评价模型的适用性,采用AUC值评估性能与不同算法模型性能对比的手段,验证了支持向量机算法为本次研究的最佳算法。
(3) 通过对仁沐新高速公路主线部分边坡的快速评价,验证模型与计算方法,结果与工程实际现场定性评价相近,吻合率达95%以上,说明采用上述指标进行红层开挖边坡的快速评价是可行的。

