基于乌鸦搜索和蜻蜓算法融合与支持向量回归预测的能效虚拟机迁移

2022-08-10 08:12许彪高坤

计算机应用与软件 2022年7期

许彪高坤

1(湖南科技职业学院人工智能学院湖南长沙 410004) 2(湖南第一师范学院信息科学与工程学院湖南长沙 410205)

0 引言

数字时代的云计算服务正在逐年稳步增加。目前的云计算服务形式包括平台即服务PaaS、软件即服务SaaS和基础设施即服务IaaS，它们以按需即付即用的方式提供给终端用户[1]。云数据中心基于终端用户的需求进行建立，数据中心充分利用各种存储元素、处理器和网络交换机为用户提供服务[2]。目前，来自用户的服务需求的增加已经转向虚拟机方向[3]。需要注意的一点是，目前美国境内的云数据中心的能源消耗已经达到30亿kWh[4-5]。数据中心的能耗在未来几年仍会以每年10%的速度增加，这不仅产生了使得全球气候变暖的温室气体，还会增加数据中心的运营成本[6-7]。

为了实现云系统高能效的负载均衡，本文将设计一种基于能效的虚拟机迁移算法。算法的主要依据是利用蜻蜓算法和乌鸦算法的融合优化和支持向量回归SVR模型设计高效的虚拟机迁移决策机制。算法主要考虑两个主要问题：(1) 系统的负载预测问题；(2) 最优化的虚拟机部署问题。基于蜻蜓算法和乌鸦算法的融合算法用于实现最优的虚拟机迁移决策，支持向量回归模型则用于预测虚拟机的负载状况和资源利用状况。算法的主要过程由三个步骤构成。首先，在考虑不同资源参数类型的情况下，需要计算主机的资源利用率，包括CPU数量、内存、指令执行性能MIPS和虚拟机的负载，这些参数直接决定了资源利用率。其次，利用支持向量回归SVR模型预测每个主机的资源利用率和负载，预测资源利用率和未来主机负载之后，即需要通过负载均衡算法作出虚拟机迁移决策。此时，虚拟机在超载主机向其他主机间的迁移是一个优化问题，该问题最后通过提出的融合乌鸦和蜻蜓算法的能效虚拟机迁移算法得到。

1 相关研究分析

本节对有关能效的虚拟机部署与迁移问题进行概述性研究，重点分析相关算法的思路和优缺点，最后给出本文算法解决的主要问题。文献[8]为了建立虚拟机迁移模型，提出了时间感知的需求模型和多组件构成的功耗模型，可以通过拥塞控制方法最小化任务的执行代价，同时降低总体执行能耗。然而，该模型缺乏导致确定调度时间窗口的灵活起始时间。文献[9]通过修正遗传算法GA提出了一种混合遗传算法HGA实现云数据中心的能效虚拟机部署。HGA可以提供更好的开发能力，并改进收敛性能，但是得到的虚拟机部署方案会导致网络负载的剧增。文献[10]提出了一种虚拟机分配的优化方法，该方法可以确保多维度资源下无死锁的资源分配，但在没有负载均衡策略时其网络负载依然过高。文献[11]提出了一种基于预测模型的虚拟机合并方法，可以预测云系统的未知负载，基于预测负载和资源的未来需求可以将虚拟机部署至最优的目标位置。即使该方法有效可行，但其扩展性和网络资源的利用率方面显得不足。文献[12]基于蜂群算法FA设计了能效虚拟机迁移算法FFO-EVMM，该算法集中于虚拟机的动态迁移决策并可降低总体执行功耗。但是，在复杂云环境中算法的鲁棒性没有得到讨论。文献[13]为了实现虚拟机迁移提出了基于虚拟机合并的蚁群算法ACS-VMC。算法通过增加虚拟机迁移次数最小化服务等级协议SLA的违例。但是文中没有对算法的性能做出量化评估。文献[14]为了实现高能效虚拟机迁移在混合云环境中，设计了基于QoS感知的部署算法，可同步实现功耗和SLA违例的降低，但算法实施中在不同主机间的虚拟机迁移过程忽略了网络开销的优化。文献[15]结合模糊逻辑策略提出了能效感知的虚拟机迁移算法，算法利用虚拟机部署和超低载主机的识别将虚拟机负载进行了有效合并，通过维持当前SLA实现了功耗的最小化。

实现能效的虚拟机迁移模型的最优化问题所面临的主要问题包括：

1) 将云系统的空闲主机转换为节能模式可以改善虚拟机的合并过程，但这会导致超载主机和低载主机的不可靠特征，即执行虚拟机动态迁移也会影响与虚拟机相关的任务执行。

2) 云系统中执行虚拟机迁移，需要考虑到每个虚拟机的资源利用，而为了实现负载均衡，最佳虚拟机的选择必须在迁移过程中得到优化决策。

3) 如文献[9]，基于虚拟机迁移的负载均衡策略忽略了云系统的能耗问题，而这是云计算系统效率的一个重要衡量指标。

4) 虚拟机迁移必须全局考虑，它会影响任务的服务质量，可能造成服务等级协议的违例。在超载主机与低载主机间进行虚拟机迁移不应该违背服务等级协议SLA[15]。

针对以上问题，本文设计基于能效的虚拟机迁移算法。算法的出发点是利用蜻蜓算法和乌鸦算法的融合优化和支持向量回归模型设计虚拟机迁移决策机制，利用支持向量回归模型预测虚拟机的负载状况和资源利用状况，利用蜻蜓算法和乌鸦算法的融合实现最优的虚拟机迁移与部署。算法的主要技术优势在于：首先，算法综合考虑不同资源类型的负载问题，包括CPU数量、内存、指令执行性能MIPS和网络带宽的负载，这些参数直接决定了资源利用率；其次，算法利用支持向量回归模型实现了主机资源利用率和负载的预测，对于超载问题可以通过负载均衡模型做出虚拟机迁移；最后，融合乌鸦和蜻蜓算法的能效虚拟机迁移则有效解决了前一步骤中的主机超载问题，实现了更均衡和高能效的虚拟机部署方案。

2 云计算中的虚拟机迁移模型

本节建立实现负载均衡时相关虚拟机迁移的基本云计算模型。如图1所示为本文所讨论的虚拟机迁移模型与框架。云计算模型由解决云用户需求的不同类型的主机PM构成，主机为了动态地处理用户任务，可部署虚拟机VM集合。云系统中的虚拟机可以动态创建以减少系统负载的瓶颈问题，同时通过虚拟化操作可以改进系统处理速率。用户请求以任务形式进入系统，每个用户任务可根据轮转方式分配在一个虚拟机上执行。主机控制其虚拟机集合，而云系统可以实现监测系统中主机上的负载。若主机负载超过设定的阈值，即认为该主机为超载主机，负载均衡模块会选择迁移该主机上的虚拟机至其他低载的主机上，从而均衡整个系统的负载，实现负载均衡。

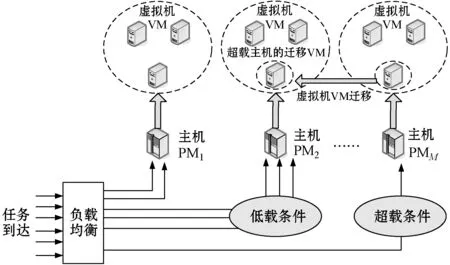
图1 云系统中的虚拟机迁移模型

(1)

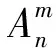
3 融合乌鸦搜索算法和蜻蜓算法的能效虚拟机迁移

图2所示为本文提出的融合乌鸦算法和蜻蜓算法的能效虚拟机迁移算法的整体框架。虚拟机迁移模型利用负载均衡策略持续检测主机的负载状况。若主机负载超过用户设置的阈值，模型将选择最佳的虚拟机在超载主机与低载主机时进行迁移，从而平衡负载状况。图2中的虚拟机迁移模型假设主机PM2是超载主机，因此，需要从中选择一个最佳的虚拟机迁移至低载的主机PMM上。本文算法模型中，利用支持向量回归SVR模型进行主机未来负载的预测，并通过负载均衡思想作出虚拟机迁移决策。

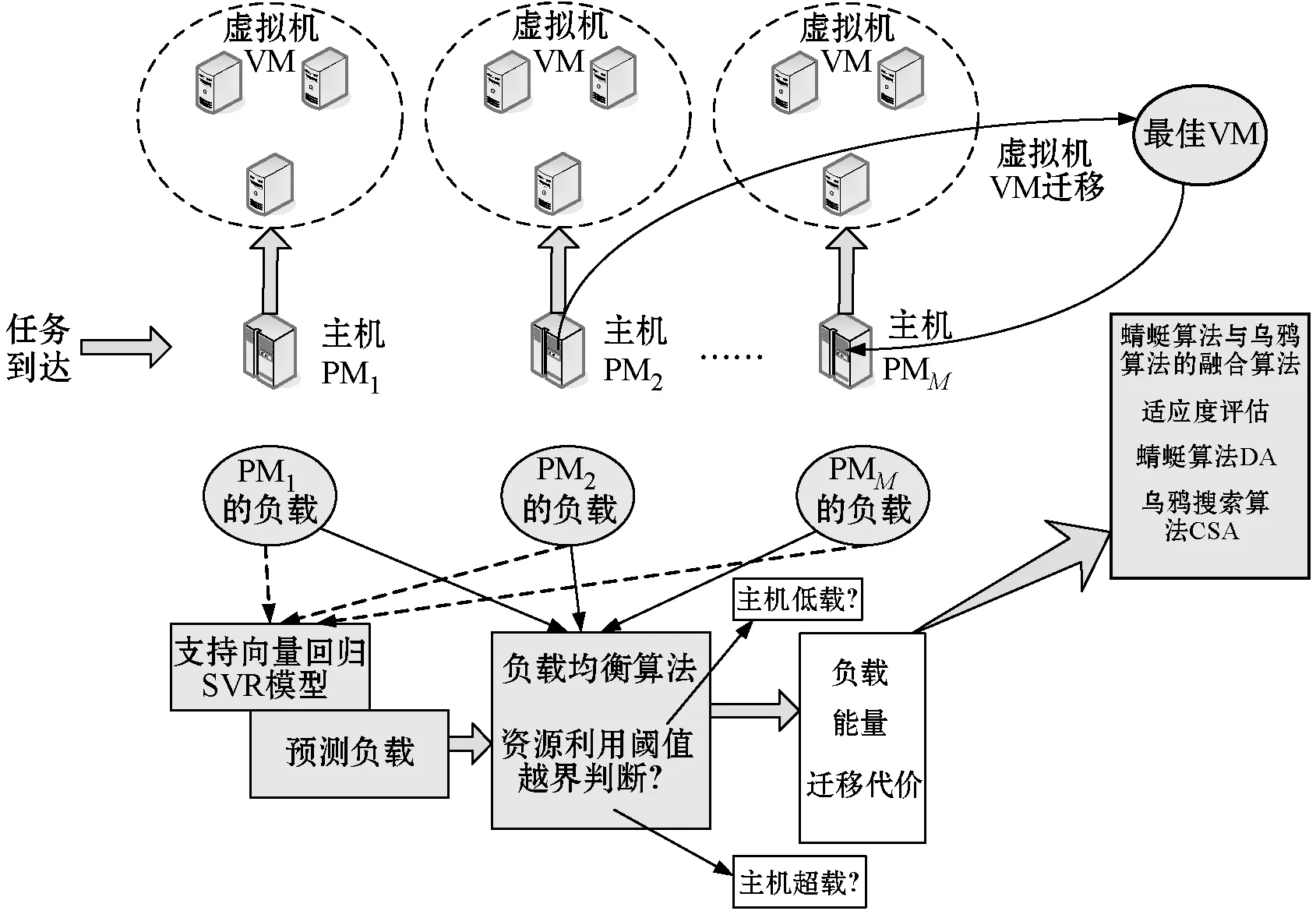
图2 算法整体框架

3.1 虚拟机迁移模型

本文在虚拟机迁移模型中考虑了系统负载、能量和迁移代价三种因素，虚拟机对于主机资源占用的属性包括CPU数量、内存、网络带宽和MIPS数量四种，这些属性均会影响系统负载状况。因此，算法需要寻找最佳的迁移虚拟机进行重新部署，从而优化负载、能量、迁移代价。以下对这三种模型分别进行说明与定义。

3.1.1负载模型

系统的负载直接决定于处理来自用户的任务时虚拟机占用的资源情况，虚拟机利用的资源主要包括CPU、内存、网络带宽、MIPS，则可将第n个虚拟机的负载定义为：

(2)

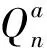
(3)

式中：QA(a)、QB(a)、QC(a)和QD(a)分别表示时间周期a时虚拟机所占用的CPU、内存、网络带宽和MIPS资源；R表示资源占用量，可定义为：

R=QA+QB+QC+QD

(4)

资源占用QA(a)、QB(a)、QC(a)和QD(a)可以表示为可变时间周期变量a内的资源利用率，定义为：

(5)

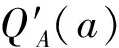
(6)

虚拟机n在内存资源上的资源占用可定义为：

(7)

(8)

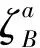
同样的道理，虚拟机n在网络带宽资源上的资源占用可定义为：

(9)

(10)

虚拟机n在MIPS资源上的资源占用可定义为：

(11)

式中：a-1和a-2代表过去的时间周期间隔内的资源占用。

(12)

主机包含一个虚拟机集合，因此，主机负载直接取决于资源占用和虚拟机负载。主机负载和主机的资源占用分别表示为：

(13)

(14)

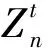
(15)

(16)

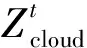
3.1.2迁移代价模型

虚拟机的动态迁移允许虚拟机在不同主机之间进行转移，虽然不存在暂停且只有较短停机时间，但动态迁移本身对于运行在虚拟机上的应用会在性能上带来负面影响。而性能下降和停机时间均取决于应用执行过程中磁盘读写页面数量。因此，虚拟机的迁移代价可以系统中发生的虚拟机移动次数进行衡量。初始情况下，可将云计算系统的迁移代价考虑为最高，值为1。将整体的虚拟机迁移代价定义为：

(17)

式中：J表示迁移常量；o表示虚拟机的移动次数；N表示虚拟机总量；M表示主机数量。

3.1.3能量模型

系统能耗取决于数据处理和迁移过程中每个虚拟机所利用的功耗，因此，云计算系统的能量直接决定于虚拟机上不同类型资源产生的功耗，而该功耗又由对应资源的负载和资源利用率决定。将云计算系统的能耗定义为：

(18)

式中：Ht表示系统中时间t时虚拟机相关网络元素的功耗(本文考虑的元素包括CPU、内存、网络带宽和MIPS)。该功耗表示为：

(19)

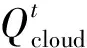
3.2 基于支持向量回归SVR的负载预测

虚拟机的负载在每个任务到达均可能出现变化，因此，有必要考虑虚拟机上的未来负载值从而选择合适的虚拟机目标。本文采用一种基于支持向量回归模型SVR的未来负载预测方法。SVR模型利用一个非线性函数集合用于将已知负载值映射为未知负载值。将主机的负载值作为回归模型的输入值，基于该值预测未来负载值。SVR模型需要的训练集合定义为：

S={(u1,v1),(u2,v2),…,(uN,vN)}

(20)

式中：u属于输入集合U；v属于输出的预测集合V。模型输入和输出间的映射可形式化为以下的最优化问题：

(21)

式中：L表示输出估算值的代价。最优化问题的约束条件为：

〈〈p,φ(un)〉+q〉-vn≤α+α+

(22)

vn-〈〈p,φ(un)〉+q〉≤α+α-

(23)

式中：α+和α-分别表示预定义的误差和高维度特征集合G中的p值；φ表示分离超平面的符号函数。SVR利用回归函数定义输出估算值的上限和下限，其回归函数定义为：

f(u)=〈p,φ(u)〉+q

(24)

此外，SVR模型利用拉格朗日对偶最大化问题进行估算值的预测，可将其表示为：

(25)

式中：βn表示拉格朗日乘子,W表示对偶函数。

以上定义的最大化问题的约束条件为：

对于拉格朗日对偶最大化问题的回归估算可表示为：

(26)

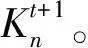
3.3 负载预测算法

本节给出负载均衡算法，通过虚拟机迁移完成均衡的负载分配。算法的主要步骤如下：

步骤1初始化云计算系统，包括M个系统主机PM和N个虚拟机VM。

步骤2初始阶段将主机的迁移代价设置为最大值，即迁移代价为1。

步骤3在时间周期t时，根据轮转方法将到达的任务分配至虚拟机。

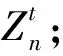
步骤5根据以下标准，选择最佳的虚拟机(基于乌鸦搜索和蜻蜓优化算法的虚拟机最优部署算法中得到)在低载主机和超载主机间进行虚拟机迁移，并更新迁移代价：

(27)

步骤6寻找系统负载值Zt、能耗、资源利用率、系统的迁移代价。

步骤7重复步骤3-步骤6进行算法迭代，直到达到终止迭代条件h。

3.4 基于乌鸦搜索和蜻蜓优化算法的虚拟机最优部署算法

3.4.1解的编码

考虑以下场景：主机PM1部署3个虚拟机，主机PM2部署2个虚拟机，到达的任务根据轮转方式分配至每个虚拟机上执行。当主机PM1超载时，PM1上的虚拟机需要迁移至PM2上，算法的目标即是选择最佳的虚拟机进行迁移。如图3所示即为解的编码方式。

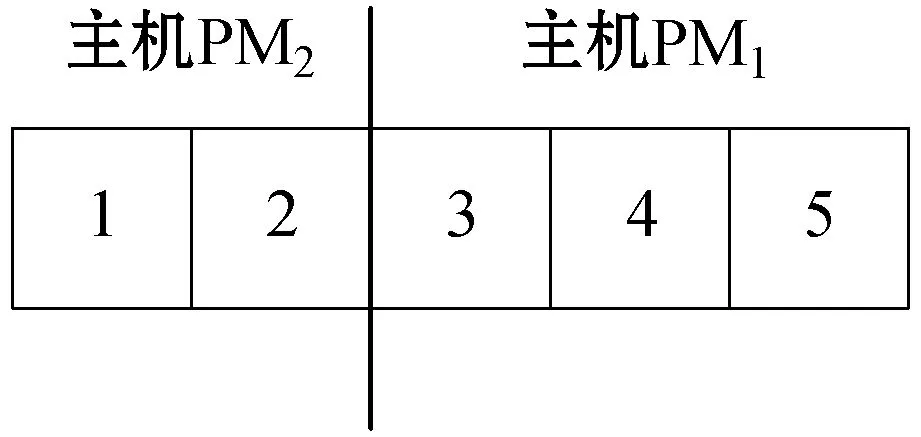
图3 解的编码

3.4.2适应度评估

适应度函数用于选择合适的虚拟机在低载主机和超载主机间迁移。本文定义了基于负载、能量和迁移代价的适应度函数，并以适应度值最大化为目标。具体将适应度函数定义为：

(28)

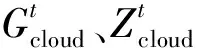
3.4.3算法具体过程

基于乌鸦搜索和蜻蜓优化算法的虚拟机最优部署的目标是选择最佳的虚拟机进行迁移，具体过程如下：

步骤1种群初始化。首先，随机初始化种群，生成种群规模为O的解集，并将其表示为：

I={I1,I2,…,Ii,…,IO}

(29)

式中：Ii表示第i个解，1≤i≤O。

步骤2适应度评估。根据式(28)的适应度函数，评估每个解的适应度。由于算法应用的适应度是最大化函数，包括最大适应度值的解被保留，可进入下一轮的迭代更新。

步骤3位置更新。蜻蜓算法DA考虑的种群元素为蜻蜓，在蜻蜓更新位置过程中，其具体属性包括：分离、队列、凝聚、食物源、敌人。DA的位置更新模式如下：

I(z+1)=I(z)+(b1X1+b2X2+

b3X3+b4X4+b5X5)+rΔI(z)

(30)

式中：X1、X2、X3、X4和X5分别表示以上5个属性上解的位置；b1、b2、b3、b4和b5分别对应于5个属性影响解的质量的权重；r表示解的惯性权重；ΔI(z)表示以上参数的位置变化。

乌鸦搜索算法CSA也是一种类似于DA的智能种群算法，其考虑的种群是乌鸦，每个解的更新取决于乌鸦的行为。CSA中位置更新方式为：

I(z+1)=I(z)+c·l(z)·(e(z)-I(z))

(31)

式中：c表示CSA更新的常量；l(z)表示迭代z时解的飞行长度因子；e(z)表示记忆。

由于DA和CSA两种算法的位置更新等式均取决于种群特征和随机初始化的种群位置，可将CSA的位置更新应用于DA的位置更新中。因此，可以寻找CSA中的l(z)值，并用于取代CSA中的位置更新值。修改式(31)得到l(z)的值，可将其表示为：

(32)

将式(32)代入式(31)中，算法得到的位置更新为：

(b1X1+b2X2+b3X3+b4X4+b5X5)+rΔI(z)

(33)

式(34)表示算法的位置更新的最终等式：

(34)

步骤4基于适应度寻找最优解。计算每个更新解的适应度，拥有最高适应度的解保留为算法的最优解。

步骤5算法终止。算法迭代结束，返回最优解。最大迭代限制定义为Y。

算法1给出了基于乌鸦搜索和蜻蜓优化算法的虚拟机最优部署算法的伪代码，算法目标是在主机到达超载条件时寻找最佳的迁移虚拟机，迁移虚拟机需要从超载主机上迁移至低载主机上。最优化过程利用了基于负载、迁移代价和能耗的适应度来决策迁移虚拟机的选择。

算法1基于乌鸦搜索和蜻蜓优化算法的虚拟机最优部署

输入:population I

//输入初始种群

输出:best solution

//输出虚拟机最优部署解

1.begin

2. randomly initialize the population of our algorithm

//对算法的种群进行随机初始化，得到初始解

3.ifz≤Y

//当前迭代次数未超过最大迭代次数

4. find the fitness value of each solution based on Equ.(28)

//根据式(28)计算每个解的适应度

5. update the position of the solution based on Equ.(34)

//根据式(34)更新解的位置

6. recompute the fitness of each solution

//重新计算每个解的适应度值

7.endif

8.ifz=Y

//到达最大迭代次数

9.returnthe optimal solution

//返回最优部署解

10.endif

11.end

4 仿真实验评测

4.1 实验环境与评价指标

通过CloudSim[16]构造仿真环境对算法的可行性和有效性进行验证，仿真实验中建立5台主机和20台虚拟机的部署环境，用户到达任务设置为100和500，以此度量算法在不同运行规模下的效率。算法的评价选择为能耗、迁移代价和负载，三个指标分别由文中式(18)、式(17)和式(15)定义，优化目标是尽可能最小化三个指标值。

选择的对比算法包括ACO算法[13]、LR算法[11]、MEGSA-VMM算法[17]和DA[18]。ACO算法执行虚拟机的分配是基于蚂蚁的搜索行为，LR算法进行虚拟机合并则是通过系统中CPU和内存利用的预测方式实现，MEGSA-VMM算法则利用了指数迁移平均模型EWMA和引力搜索算法GSA进行虚拟机的优化部署过程，DA则是传统的蜻蜓算法过程。

4.2 实验结果分析

实验1测试了100个用户预测任务到达时算法的性能表现，结果如图4所示。在首次算法迭代中，ACO、LR、MEGSA-VMM和DA得到的负载指标值分别为0.57、0.29、0.07和0.075。本文算法得到的负载指标值为0.07，是所有算法中最低的。同样，在能耗方面，本文算法在首次迭代中得到了所有算法中最小的能耗值为0.016。而在迁移代价方面，本文算法同样是最优的。换言之，负载、能耗、迁移代价三个指标值上，本文算法均得到了最小值，则适应度相应是所有算法中最大的，性能表现是最好的。原因在于：支持向量回归机制可以利用非线性函数集合将所取样的已知负载值映射为未知负载值，以主机负载值作为回归模型的输入值，可以较为准确地对主机的未来负载作出决策，预防出现热点而导致性能下降，为优化虚拟机的具体部署打好了基础。而融合入蜻蜓算法和乌鸦算法的虚拟机部署策略则在超载情况下的虚拟机迁移选择上作出了最优决策，通过融合两种算法在局部开发和全局搜索上的优势可以使得虚拟机迁移在满足负载均衡的同时得到最小化系统能耗。

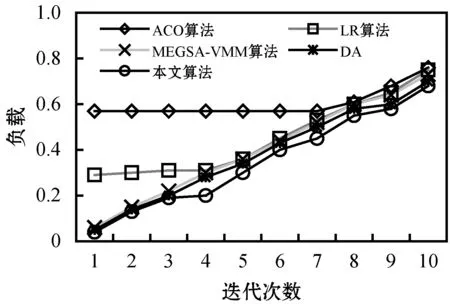
(a) 负载状况

图5是将任务量增加至500时得到的算法性能表现。可以看出，增大任务规模并没有对本文算法的执行效率产生反转式影响，其在负载、能耗和迁移代价三个指标上依然稳定地优于另外四种对比算法，这说明所采用的支持向量回归的负载预测机制和融合入蜻蜓算法和乌鸦算法的虚拟机部署策略依然是有效可行的，不仅可以对虚拟机迁移选择做出正确决策，而且能够使得虚拟机迁移在满足负载均衡的同时最小化系统能耗，具有全局最优的执行效率。