既有建筑绿色改造参与者的行为演化博弈分析

朱红章，汪 雷

（武汉大学土木建筑工程学院，武汉 430072）

根据《2019 中国建筑能耗研究报告》［1］，中国建筑能耗总量明显上升，占全国能耗比重为21.11%；建筑碳排放20.44 亿t CO2，占全国能源碳排放的19.5%。在建筑行业高速发展和推行可持续发展的背景下，现有建筑的绿色改造成为未来发展的重要方向［2］。虽然中国绿色建筑得到大力推广，但是要实现中国在建筑能源与绿色建筑“十三五”规划中提出新增绿色建筑面积达12 亿m2以上的目标仍然有诸多阻碍［3］。此时，既有建筑的绿色改造成为中国建筑行业的一项重要选择［4］。针对建筑的节能改造发展，国内外学者开展了大量研究。金占勇等［5］研究发现推行节能建筑，能在一定程度上缓解中国的能源需求。Baek 等［6］认为，绿色改造在建筑行业的推广中存在诸多困难，包括经济制约和政府监管等。因此，如何有效促进既有建筑节能改造的推广显得尤为重要。

学者们对如何推动既有建筑的节能改造做了一系列研究。侯静等［7］讨论了政府的经济刺激对建筑节能改造的影响，认为经济激励有利于行业的推广发展。Bertoldi 等［8］通过对比西方各国的节能改造项目，指出政府在节能改造项目推广过程中起积极作用。Hori 等［9］通过问卷调查的方式，认为政府和业主在一定程度上影响了企业节能改造的服务质量。王波［10］分析了政府补贴条件下施工企业和建设单位的策略选择，研究表明政府补贴后博弈双方开发绿色建筑意愿更强。梁喜等［4］在不考虑政府政策对消费者作用的情况下，讨论了绿色建筑供给侧的演化稳定策略。刘晓君等［11］探讨了建筑节能改造参与者的利益分配关系。

综上所述，既有建筑的节能改造是建筑行业发展的趋势，但是目前节能改造的推广仍然面临企业开发成本高、消费者购买意愿低等阻碍，迫切需要政府用政策激励企业积极进行既有建筑的节能改造。虽然已有学者研究表明政府的经济激励对节能改造的推广有积极作用，但是相关研究的行为博弈往往是建立在经典博弈的理论基础上，有些仅考虑了单种群行为，忽略了消费者对政府和企业决策的影响［12］，或是为了简化分析不考虑政府补贴对消费者的作用［4］。而且在政府激励企业开发绿色建筑的过程中，三方的博弈应该是反复持续进行的。因此，本研究从动态的角度出发，构建主体为政府、消费者和企业的演化博弈模型，求解不同情形下的演化稳定策略，并通过数值仿真研究绿色建筑开发的影响因素，为促进既有建筑的节能改造提供一定的依据。

1 构建建筑节能改造参与者演化博弈模型

1.1 模型假设

1）博弈主体。政府激励企业节能改造的过程中，涉及的利益主体为企业（开发商）、消费者和政府。企业的决策始终以盈利为目标；消费者综合建筑的实际效用和购买力进行决策；政府为了促进企业改造既有建筑，给予企业资金补贴和政策扶持。博弈主体均具有行为感知能力、学习能力和调整能力，并且决策均为各自的利益最大化，在三方博弈行为的演进过程中寻求最佳策略。

2）博弈主体的行为策略。假设政府可选择的行为集合都为M1=｛补贴，不补贴｝，对应的概率为x和1-x；假设消费者的决策集合为M2=｛购买，不购买｝，对应的概率为y和1-y；假设企业可以选择的策略集合为M3=｛改造，不改造｝，对应的概率分别为z和1-z。

3）各方损益参数设置。假设当企业选择进行建筑节能改造时，不考虑其他参与者的初始意愿，企业已成功改造既有建筑，已经损失其成本；假设当政府选择补贴，但是消费者不购买建筑或开发商不改造建筑时，政府不损失其补贴成本；假设当消费者选择购买节能改造建筑，企业拒绝进行建筑节能改造，消费者不损失其购买建筑节能改造的增量成本。博弈主体的损益参数如下。

对政府而言，当企业选择“不改造”时，政府的收益为A1；当企业选择“改造”时，政府会获得因建筑成功节能改造带来的声誉收益和环境收益等增量收益，记为ΔA1。此时，政府补贴企业进行建筑节能改造的成本记为A2，相应地，消费者选择“购买”可以获得的政府补贴为γA2，γ为政府补贴系数。

对消费者而言，消费者策略为“不购买”时，可以获得的收益为B1；如果消费者策略为“购买绿色建筑”，消费者获得的环境效益和节能收益等增量收益记为ΔB1；消费者策略为“购买”的成本为B1，“购买”耗费的增量成本为ΔB2，同时消费者可以获得政府给予的补贴γA2。

对企业而言，企业选择“不改造”时，可以获得的收益为C1，对应的开发成本为C2。企业选择“改造”时，获得的社会收益等增量收益记为ΔC1，相应的增量成本记为ΔC2。同时，为了研究消费者从选择“不购买”转向“购买”对企业是否对既有建筑进行节能改造决策的影响，本研究将消费者选择“购买”节能改造的建筑时给企业带来的增量收益记为C3，不包含在ΔC1内。

1.2 建立三方博弈支付矩阵

根据上述假设，构建三方博弈支付矩阵，如表1所示。

表1 支付矩阵

2 演化博弈模型的建立

2.1 博弈主体的复制动态方程

消费者选择“购买”策略时，消费者的期望收益为：

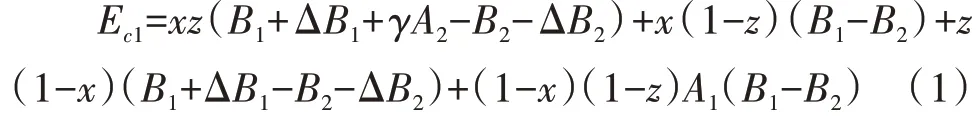
消费者选择“不购买”策略时，消费者的期望收益为：

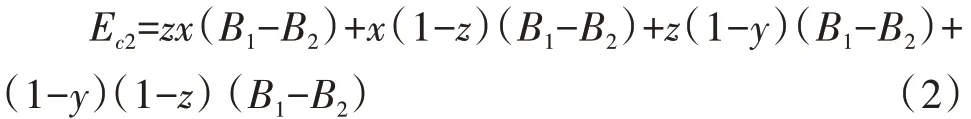
所以消费者的平均期望收益为：

此时，消费者选择“购买”策略的复制动态方程为：

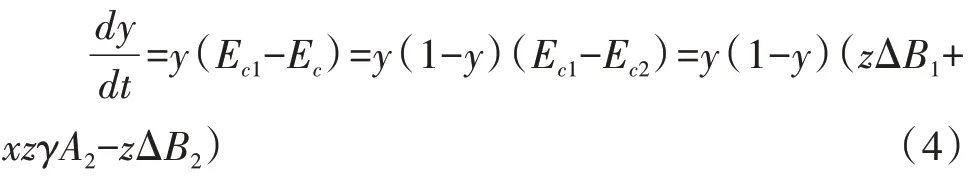
政府选择“补贴”和“不补贴”策略时期望收益如下：

此时，政府选择“补贴”策略的复制动态方程为：

企业选择“改造”和“不改造”策略时的期望收益分别如下：

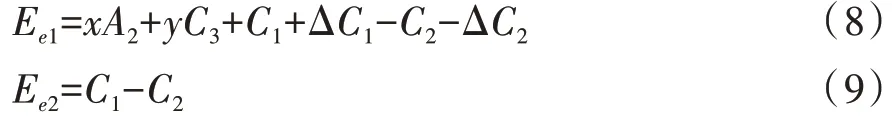
此时，企业选择“改造”策略的复制动态方程为：

此时，整理公式（4）、公式（7）和公式（10），即得该演化系统的复制动态方程组。

2.2 博弈主体演化稳定性分析

为了探索政府、消费者和企业三方的博弈演化趋势，下面分别分析三方的演化稳定性。

1）政府演化稳定性分析。政府选择演化策略的稳定性判断条件为F（x）=0＜0。令F（x）=0，可得x=0，x=1，y=。

如果，F（x）始终为0，政府处于稳定状态。

如果y≠，则x=0 和x=1 是方程的2 个可能稳定点。对F（x）求导可得：

当1>y>>0 时，在点x=0 处，＜0，于是x=0 为稳定点；在点x=1 处，＞0，于是x=1为非稳定点。表明政府如果选择“补贴”时，所获得的收益小于补贴的成本，此时政府选择“不补贴”为策略演化趋势。当1>>y>0 时，在点x=0 处，＞0，所以x=0为非稳定点；在点x=1处，＜0，于是x=1为稳定点。表明政府如果选择“补贴”时，所获得的收益大于付出的补贴成本，此时政府选择“补贴”为策略演化趋势。

2）消费者演化稳定性分析。消费者演化稳定策略稳定性的判别条件为F（y）=0＜0。令F（y）=0，可得y=0，y=1，x=

。

如果x=，F（x）始终为0，消费者处于稳定状态。

如果x≠，则y=0 和y=1 是方程的2 个可能稳定点。对F（y）求导可得：

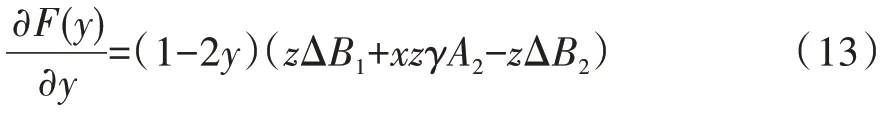
当1>x>>0时，在点y=0处，＞0，所以y=0为非稳定点；在点y=1处，＜0，此时y=1为稳定点。表明消费者如果选择“不购买”，所获得的收益小于选择“购买”时获得的收益与补贴，此时消费者选择“购买”的策略趋势。

如果y=，F（z）始终为0，为稳定状态。

如果y≠，则z=0 和z=1 是方 程的2 个可能稳定点。对F（z）求导可得：

当1>y>>0 时，在 点x=0 处，＞0，于是z=0为非稳定点；在点z=1处，＜0，于是z=1 为稳定点。表明此时企业选择“不改造”获得的收益小于“改造”时获得的收益和补贴，所以企业选择“改造”的策略趋势。

4）混合策略演化稳定性分析。参考Ritzberger等［13］的研究，系统的策略空间由系统纯策略均衡点得到。系统的策略空间为｛（x，y，z）|0≤x≤1，0≤y≤1，0≤z≤1｝。根据Friedmand［14］的分析，演化系统均衡点的稳定性可由雅各比矩阵的局部稳定性得出。系统的雅各比行列式J表示如下。

策略空间的顶点为P1（0，0，0）、P2（1，0，0）、P3（0，1，0）、P4（0，0，1）、P5（1，1，0）、P6（1，0，1）、P7（0，1，1）、P8（1，1，1），分别带入雅各比矩阵，计算可得矩阵特征值，结果如表2 所示。

表2 雅各比矩阵的特征值

由于影响系统稳定性的因素较多，本研究对雅各比矩阵特征值分开讨论，通过分析不同情形下特征值的符号确定演化策略稳定点。

对于特征值λ1，分为3 种情形讨论。情形1，企业选择进行既有建筑的节能改造带给政府的收益大于政府的总补贴成本，即ΔA1-A2-γA2＞0。情形2，企业选择“改造”带给政府的收益小于政府的总补贴成本，但是大于政府给予企业的补贴成本，即ΔA1-A2-γA2＜0，ΔA1-A2＞0。情形3，企业选择“改造”带给政府的收益小于政府的总补贴成本，也小于政府给予企业的补贴成本，即ΔA1-A2-γA2＜0，ΔA1-A2＜0。每种情形下对应的特征值符号如表3 所示。

表3 矩阵特征值λ1

对于特征值λ2，分为2 种情形讨论。情形Ⅰ，消费者选择“购买”带来的增量收益大于增量成本，即ΔB1-ΔB2＞0。情形Ⅱ，消费者选择“购买”带来的增量收益小于增量成本，但是在政府补贴后消费者收益大于其成本，即ΔB1-ΔB2＜0，γA2+ΔB1-ΔB2＞0。每种情形下的特征值符号如表4 所示。

表4 矩阵特征值λ2

对于特征值λ3，讨论的情形为企业选择“改造”的增量成本大于企业选择“改造”策略时带来的直接增量收益，但是小于政府选择“补贴”或消费者选择“购买”时企业的总收益，即ΔC2-ΔC1-A2＜0，ΔC2-ΔC1-C3＜0，ΔC2-ΔC1＞0。该情形下的特征值符号如表5 所示。

表5 矩阵特征值λ3

综合表3、表4 和表5，本研究讨论了6 种情形组合，每种情形组合的平衡点局部稳定性如表6 所示。

根据表6 可知，在情形组合（1、Ⅰ）和（1、Ⅱ）条件下，演化趋于点（1，1，1）。在情形组合（2、Ⅰ）和（3、Ⅰ）条件下，最终演化结果趋于（0，1，1）。对于情形组合（2、Ⅱ）和（3、Ⅲ），三方演化博弈没有稳定点。

表6 稳定性分析

3 模型仿真分析

3.1 建立SD 模型

为了反映各项参数对三方博弈模型的动态影响，基于Vensin 软件平台以及博弈主体不同决策条件下的期望收益函数和复制动态方程，结合系统动力学建立政府、消费者和企业参与既有建筑节能改造项目的演化博弈模型，如图1 所示。该SD 流图由3 个状态变量、3 个流率变量、9 个辅助变量和13 个外部初始变量构成。

图1 博弈主体参与建筑绿色改造的SD 流图

3.2 模型仿真模拟

参考文献［15］的初始假设，仿真起始时间INI⁃TIAL TIME=0，步长TIME STEP=0.007 812 5，结束时间FINAL TIME=100 m，进而模拟不同情形组合下政府、消费者和企业的演化趋势。

在情形（1、Ⅰ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=3.0、γA2=1.2、B1=1.0、B2=0.7、ΔB1=1.2、ΔB2=1.0、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。在情 形（1、Ⅱ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=3.0、γA2=1.2、B1=1.0、B2=0.7、ΔB1=1.0、ΔB2=1.2、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。三方初始的意愿设置为x=y=z=0.1。模拟结果如图2 和图3 所示。

分析可知，当企业选择“改造”带给政府的收益ΔA1大于政府的补贴成本，消费者选择“购买”的收益大于购买普通建筑时，政府、企业和消费者的趋势都是建筑的节能改造。纵向对比图2 和图3 可以发现，在“购买”带给消费者的增量收益减小时，博弈主体的策略演化结果虽然都趋向于（1，1，1），但是演化所需的时间更长。反映出已有建筑节能改造带给博弈主体的收益，有助于提高政府的积极性，激励企业的改造意愿，也有助于提高消费者购买的意愿。

图2 情形（1、Ⅰ）的演化趋势

图3 情形（1、Ⅱ）的演化趋势

在情形组合（2、Ⅰ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=2.5、γA2=1.2、B1=1.0、B2=0.7、ΔB1=1.2、ΔB2=1.0、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。在情形组合（3、Ⅰ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=1.0、γA2=1.2、B1=1、B2=0.7、ΔB1=1.2、ΔB2=1.0、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。三方初始的意愿设置为x=y=z=0.1。 模拟结果如图4 和图5 所示。

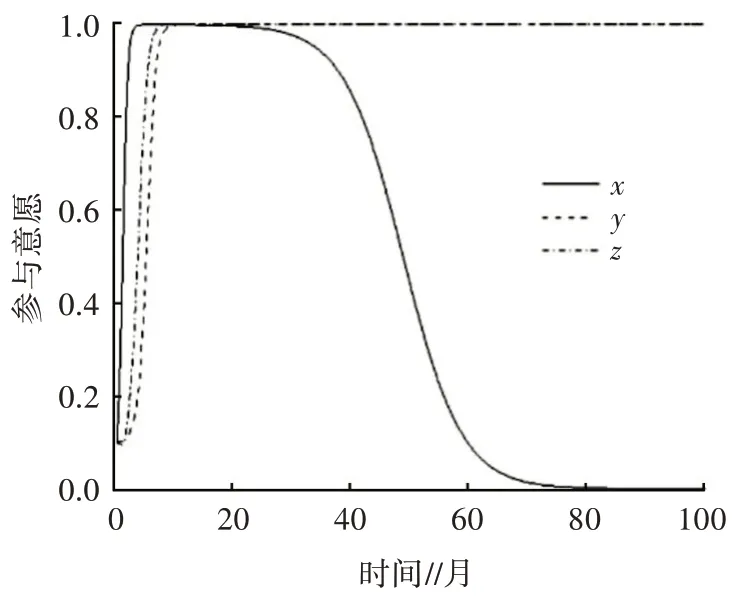
图4 情形（2、Ⅰ）的演化趋势

图5 情形（3、Ⅰ）的演化趋势

分析图4、图5 可知，在“购买绿色建筑”带给消费者的增量收益较大时，消费者会积极选择“购买”既有建筑节能改造，企业也会因为消费者的积极购买增加收益，此时政府“补贴”与否都不会影响企业和消费者的演化趋势，所以政府选择减少补贴成本，最终结果趋向于（0，1，1）。纵向对比图2、图4 和图5可以发现，随着建筑的节能改造带给政府的收益降低时，政府逐渐趋向于不补贴，而且演化过程所需的时间增长。

在情形（2、Ⅱ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=2.5、γA2=1.2、B1=1.0、B2=0.7、ΔB1=1.0、ΔB2=1.2、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。在情 形（3、Ⅱ）条件下，初始参数设置为A1=1.7、A2=1.5、ΔA1=1.0、γA2=1.2、B1=1.0、B2=0.7、ΔB1=1.0、ΔB2=1.2、C1=1.2、C2=1.0、ΔC2=2.5、C3=0.7。三方初始的意愿设置为x=y=z=0.1。模拟结果如图6 和图7 所示。

图6 情形（2、Ⅱ）的演化趋势

在企业“改造”带给政府的收益较少，而消费者购买建筑节能改造时收益与否取决于政府是否补贴时，三方博弈的演化过程缺少稳定点，始终处于动态演化的过程，已有建筑的节能改造的推广较慢，这种情况不利于绿色建筑的普及发展。图6、图7 同图2、图3、图4 和图5 纵向对比可以发现，建筑节能改造带给博弈主体的增量收益越大，政府、消费者和企业都更倾向于建筑的节能改造，而且演化过程所需的时间也更短。

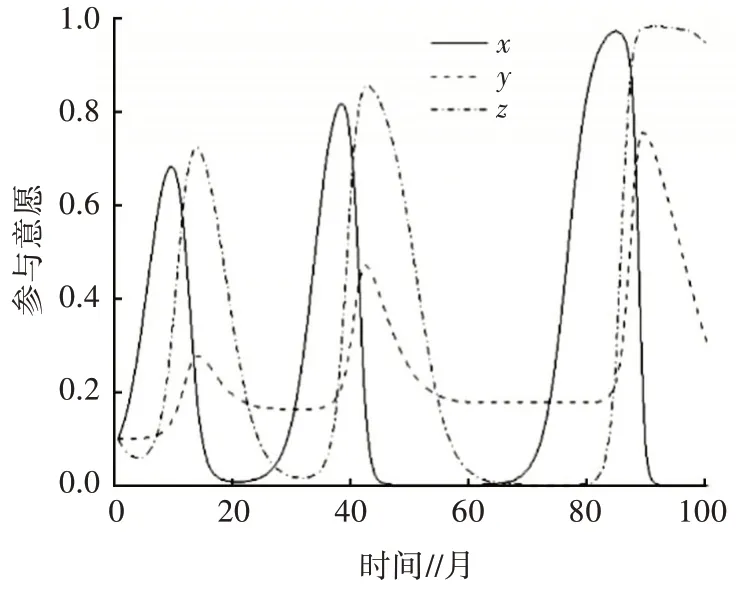
图7 情形（3、Ⅱ）的演化趋势

4 结论与启示

本研究基于演化博弈综合分析政府、消费者和企业在既有建筑节能改造推广过程中的作用，结合系统动力学模拟了不同影响因素对演化趋势的影响，得出的相关结论如下。

1）演化博弈弥补了传统博弈论完全理性假设的不足，结合系统动力学理论，可以直观地展示动态演化过程。

2）建筑的节能改造会带给绿色建筑项目参与者一定的额外增量收益，增量收益的多少是建筑节能改造推广的关键要素。企业可以通过革新施工工艺减少其改造成本，提高企业经济收益的同时，带给社区消费者更优越的生活环境，增加消费者的生活舒适度，提高政府的环境效益和政府声誉。政府可以严格把控绿色改造的验收标准，提高既有建筑节能改造的环境效益，进而提高政府的增量收益，提高政府的补贴意愿。

3）政府的补贴与政策激励在一定程度上可以起到促进建筑改造推广的作用，但是长期以往会加重政府的经济成本，而且在建筑节能改造的收益降低时，政府补贴的激励效果也会降低。政府可以通过精简机构强化预算约束，推动其市场自动化，减少政府的激励成本。