遍历算法在热防护服设计中的应用

董亚玲 雷亿辉＊ 刘倩岚

（吉首大学数学与统计学院，湖南 吉首 416000）

0 引言

在高温环境下， 工作人员需要穿着特定的热防护服防止皮肤被灼伤、烫伤，因此设计出性能良好的热防护服能最大限度地保护高温工作者的生命安全。 国内已有很多学者对热防护服传热模型及防护服厚度设计进行了研究，如王宝等基于分数阶偏微分方程，结合粒子集群法和遗传算法得出了多层热传递温度分布规律和特定条件下的最优厚度； 王志强等运用Pdepe 算法、遗传算法、迭代算法等分别建立了空气层和单层固态热传导模型、空气层和三层织物层混合模型，得到了皮肤表层温度分布关系和热防护服装的最优厚度；谷韬等对带随机Robin 边界条件的一类三层抛物型方程进行了数值求解， 并基于区间算法思想计算了给定设计目标下的厚度参数置信区间。国内文献大多利用微分方程进行厚度求解，而在实际应用中，因受边界条件约束、算法设计复杂等，导致最优厚度的求解不易，甚至易陷入局部最优解。因此，本文基于已建立的热防护服传热模型， 采用遍历算法对非线性规划问题进行求解， 解决特定高温作业时间条件下热防护服各层厚度的优化设计问题。

遍历算法是指沿着某条路线进行搜索，依次对二叉树中的每个节点做一次且仅做一次访问，访问的节点所做的操作依赖于具体的应用问题，进而在空间范围内穷举出问题所有的可能性，最终根据实际问题的约束条件或目标函数筛选出符合条件的解。 遍历算法可以简化计算，快速求得不同需求下热防护服各层的最优厚度，提高工作效率。

1 遍历算法求解热防护服材料厚度

1.1 已建立模型的介绍

通过拟合分析实验数据及修正模型后，建立了拟合效果良好的温度分布模型：

其中：T（t）为人体表皮温度；T（t）为各层材料的当前温度；T表示人体与外界达到热平衡时的稳定温度，根据实验数据可知T=48.08℃；ΔQ 为热量传递量；c 为材料的比热容；ρ 为材料的密度；α 为含控制参数的阻滞因子，取α=0.0148 时模型的拟合度最优。

1.2 基于具体问题求解各层厚度

问题一研究特定条件下热防护服单层材料的厚度设计。 在环境温度为65℃、IV 层的厚度为5.5 mm的条件下，确保工作60 分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5 分钟，求出满足条件的第II 层最优厚度。

问题二研究当环境温度为80℃时， 确保工作30分钟时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5 分钟，确定II 层和IV 层的最优厚度。热防护服各层材料参数如表1 所示。

表1 专用服装材料的参数值

1.2.1 问题一模型的建立与求解

热阻与物体的厚度成正比，物体越厚，热阻越大，隔热材料传导的热流量越少。因此材料层的厚度越大，隔热效率越好。但是随着材料层的厚度变大，成本也会变高。考虑到最优成本问题，选取恰好满足温度的临界条件，建立关于第Ⅱ层材料的最小成本优化模型：

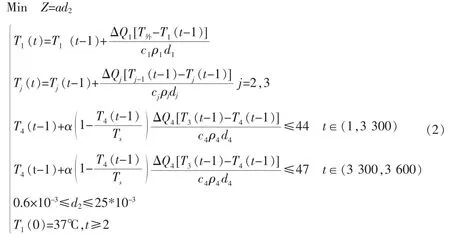
其中，α 为每利用一单位材料Ⅱ需要的成本；Z 为热防护服的成本。 由（1）式可知，当第Ⅱ层的厚度为6 mm时，可知α≈0.014 8。 随着第Ⅱ层厚度变大，对热量传递的阻滞作用也越大，因此α 随第Ⅱ层厚度的增加而减少。

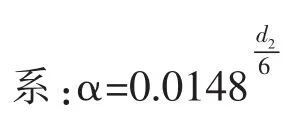
图1 第Ⅱ层材料为10.2 mm 时假人皮肤表层温度随时间变化

从图1 可以看出， 在时间为55 分钟时， 温度为43.99℃，时间为60 分钟时温度仅为44.34℃，满足了在44℃以上的时间不超过5 分钟，且最高温度不高于47℃的要求。

1.2.2 问 题 二 模 型 的 建 立与求解

保护高温工作者的人身安全，降低热传输，避免灼伤皮肤是对专业热防护服的第一要求。当假人在高温环境下静止，由表1 可知第Ⅳ层的材料导热率为0.028 W/（m.℃）， 在静止条件下空气能起到非常好的隔热效果。当面料与传感器之间空气层厚度小于6.4 mm 时， 由于空气层间隙太小，从而无法形成对流运动，这时空气的热传递以传导为主。

当高温工作者离开高温环境后，储存在热防护服内部空气中的热量随时会释放，也会对工作者造成二次灼伤。 因此，第Ⅳ层的厚度要尽可能大，减少热防护服内部的热量储存。 但同时由于第Ⅳ层的存在会对人体的行动以及舒适程度产生一定影响，第Ⅳ层与皮肤表层间隔过大，会影响人体的便利程度和舒适感。 因此结合热防护服最小成本构造两个目标函数：

Min Z=ad

Max F=bd

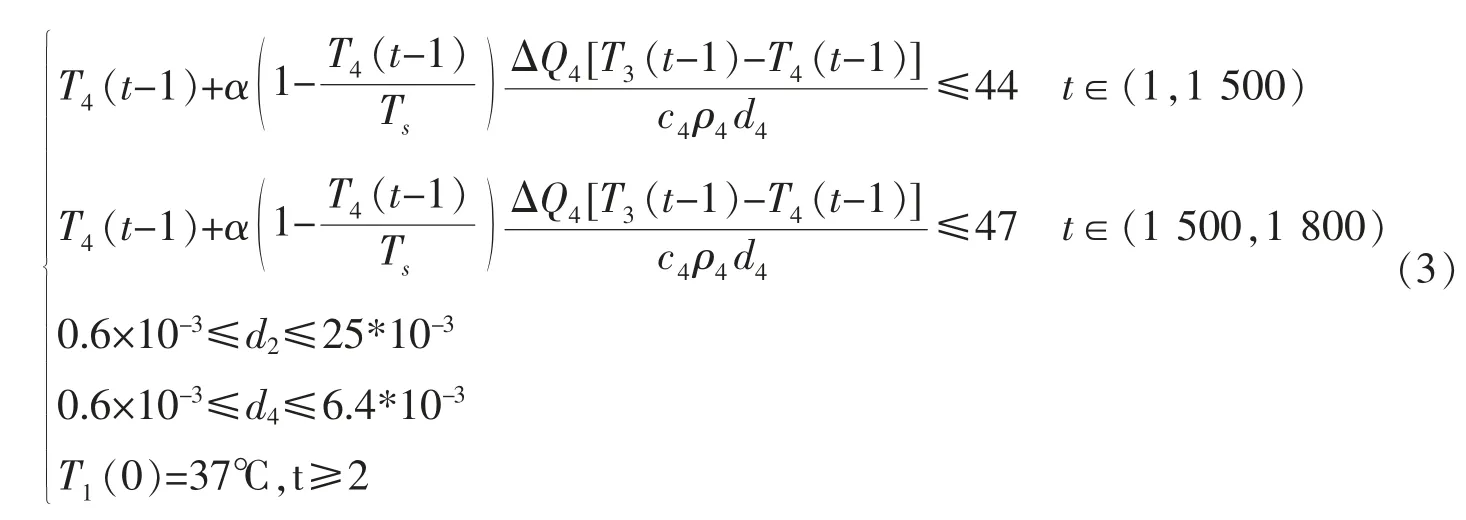
其中，Z 表示热防护服成本；F 为人体舒适程度；b为第Ⅳ层厚度对舒适程度的影响系数。

由于Ⅱ、Ⅳ层材料的厚度变化范围不大，因此通过遍历算法搜索出第Ⅱ层材料与第Ⅳ层材料厚度的组合，并根据模型筛选出最优可行解。 求解得到第Ⅱ层材料的最优厚度为9.4 mm；第Ⅳ层材料的最优厚度为6.3 mm。 控制了第Ⅱ层材料的最小成本，同时使得第Ⅳ层材料的厚度最优，能够尽量降低高温工作服对人体进行二次灼伤的可能性，也能最大限度地保证人体的舒适便利程度。 在第Ⅱ层和第Ⅳ层材料最优的条件下假人皮肤表层温度随时间的变化如图2 所示。

图2 第Ⅰ、Ⅳ层材料最优时假人皮肤表层温度随时间变化

从图2 可以看出，当时间为第1 500 秒时，皮肤表层温度为43.99℃，当时间为第1 800 秒时，皮肤表层温度为44.83℃，满足给定条件。

3 结语

通过现有的温度分布模型，建立了热防护服在不同要求下的厚度决策模型。并结合最小成本问题和人体舒适度问题，利用遍历算法求解得出两种不同作业要求的情况下热防护服第Ⅱ层和第Ⅳ层的最优厚度。 经过实际计算可知，遍历算法计算简单、高效，弥补了利用微分方程求解不易的不足，并且适用范围较广，可以求解热防护服在特定情况下的各层厚度，具有较高的推广可能性。