组合数学魅力浅析
——表格里的组合证明
郝小健 凌 浩 张康群
南京工程学院数理学院 江苏南京 211167
组合数学又称离散数学,是研究离散结构的存在、计数、分析和优化等问题的一门学科,其在群论、概率论、数理统计学、粒子物理学及计算机相关领域均有着重要的应用。特别是近些年来,随着人工智能的迅猛发展,组合数学已成为一个非常活跃的数学分支[1]。高等院校对于组合数学的教学工作日益重视,许多高校都将组合数学作为面向数学及计算机专业开设的重要选修课程。
不得不提的是,由于组合数学主要考察离散结构,强调构造性证明,涉及的组合物体性质繁多且联系紧密,研究问题的技巧更是千变万化,是一门非常具有挑战性的科目[2]。正因为如此,许多同学在选课时往往将其作为第二甚至第三选择,在同等学分的前提下尽量避开这门科目,选择一些相对简单,容易通过的科目。
众所周知,兴趣是学习最好的老师。孔子有言:“知之者不如好之者,好之者不如乐之者。”事实上,无论是以赫尔巴特为代表的“传统教育”学说,还是以杜威为代表的“现代教育”学说,都将兴趣置于十分关键的地位[3]。由此,笔者希望通过本文使同学们认识组合数学,感受组合证明的魅力,培养同学们对于组合数学的兴趣。
一、组合数学的引入
笔者认为组合数学的课程引入环节非常重要,它会影响同学们对于课程的判断,进而左右其选课意愿。因此,笔者希望借助部分中小学知识作为铺垫,由熟悉至陌生,由简单到复杂,让同学们意识到组合证明并没有想象中的百转千回、变幻莫测。同学们只是习惯了连续性思维,对于离散性思维感到陌生和本能的抗拒,而这些都是不难克服的。
其实许多同学平时接触的问题都可以通过组合方法给出简洁优美的证明。例如,自小学阶段就烂熟于心的求和公式:
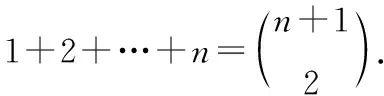
当初笔者的老师是借助首尾相加的方式来推导这个公式的,而本文则希望给出一个组合证明,从全新的角度解读上述公式,也让同学们意识到构造性证明远非想象中那么困难。
组合证明的前提是对等式两端进行组合解释,即选择恰当的组合物体被等式两端的数字所计数,这也是组合证明的准备环节。为了让同学们更好地了解构造性证明,本文选取日常工作生活中所熟悉的表格作为证明工具,让同学们切身感受到,离散性思维训练至巅峰,则“飞花摘叶皆可伤人,草木竹石亦为锋刃”。
红色 蓝色
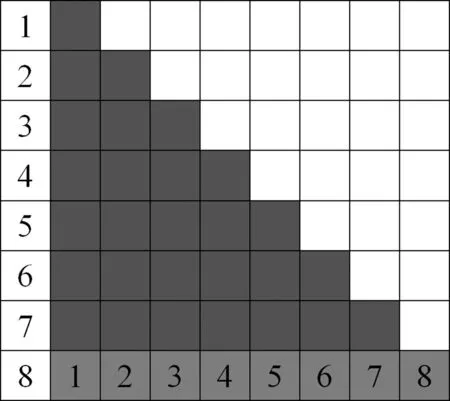
不失一般性,我们取n=7,并对等式左端进行组合解释:自上而下,自左至右依次染红第一行的第一个格子,第二行的前两个格子,直至第七行前七个格子。显然所有的红格数目为:
1+2+3+4+5+6+7.


红色 蓝色
任取一个红格,例如第四行第二个(这里我们以浅红色标示),作过其中心及底边中点的直线和过其中心及右下角顶点的两条直线,这两条直线分别穿过第八行两个不同蓝格的中心,取出这两个蓝格(以第四行第二个红格为例,即须取出第二及第六个蓝格)。至此,笔者建立了一个简洁的映射。注意到对于任意两个蓝格,同学们反向操作也可以唯一确定一个红格,从而该映射是一个一一映射,笔者也给出了上述求和公式的组合证明。
通过该题,笔者希望同学们认识到组合证明虽然注重构造,技巧性很高,但是并不是每一个都那么复杂,熟练地掌握组合解释,组合证明可以简洁而有趣。并且本部分证明用到的工具是大家日常生活经常接触的表格,很容易被理解。这样的教学方式从全新的角度给出了理解问题的方法,对于公式的记忆和应用都是大有帮助的。
二、组合数学的展开
在引入组合数学以后,笔者希望从现在大学生的日常生活出发,拉近同学们与组合数学之间的距离。比如,同学们所熟知的三国时期著名的军事家诸葛亮,在一部手游当中就有一款精致的专属皮肤叫作“黄金分割率”,而与其相匹配的台词更是飘逸与雄浑并立:“完美的几何学者,以斐波那契数列分割战场”。显而易见,即便没有经过高等数学训练的人也一定听说过黄金分割率,隐约知晓这个数字是0.618。事实上,黄金分割率有着广泛的应用,尤其是在工艺学、建筑学以及美学等方面,而这一比例和一个著名的组合序列——斐波那契数列紧密相关。
斐波那契数列是由十一世纪意大利数学家斐波那契通过理想状态下兔子的繁殖情况引入的。其在现代物理、准晶体结构以及化学等领域都有着直接的应用。为此,美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的数学杂志,用于专门刊载这方面的研究成果。组合数学中斐波那契数列一般通过如下递推公式来定义:
f1=1,f2=2,fn=fn-1+fn-2(n>2).
斐波那契数列有许多广受关注的有趣性质。例如:
相信同学们初看这个性质会有一些摸不到头脑,大都希望借助递推公式进行推导,这样难免过程烦琐。笔者希望本文的组合证明能带给同学们耳目一新的感觉,让同学们进一步领略组合数学的魅力。通过前述等差数列求和公式的组合证明,笔者认为同学们不难发现组合证明的前提是建立恰当的组合解释。而斐波那契数列极高的关注度,使其拥有很多组合解释,结合本文的主题,笔者选取其中与表格覆盖相关的一个。
首先我们生成一个1行n列的表格。继而我们用1×1的蓝格及1×2的红格来对上述表格进行覆盖,则覆盖该表格的方法数即为fn。这个结论的证明非常直接,同学们只需考虑覆盖时放的第一块是红格还是蓝格即可。


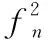
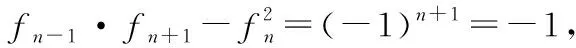

红色 蓝色
通过上述观察可知,造成左右两侧覆盖方式差值的原因恰恰在于极右切割线存在与否,如果存在就可以依极右切割线进行前述切割换表的操作。讲解到这里,笔者希望引导同学们做出另外一个重要的观察:如果位于上侧的表格包含蓝格,则该蓝格左右两侧缝隙所对应的两条垂线中至少有一条不切割下侧的表格,从而极右切割线必然存在。因此,上方表格是否一定存在蓝格就是影响等号右侧-1幂次的关键。容易看出,当n为偶数时n+1为奇数,从而左侧两个表格按照上图方式进行堆叠时,极右切割线必然存在,继而左侧覆盖方式小于等于右侧覆盖方式。根据蓝格不出现准则不难发现,当n为偶数时,除了右侧上下方均为红格的覆盖方式以外,我们都可以找到一个左侧的覆盖与之相对应,从而右侧的覆盖方式仅仅比左侧多1,反之亦然。下图分别给出了两侧堆叠表格无法通过切割换表所映射掉的特殊覆盖。

红色
至此,笔者完成了对上述性质的组合证明。这个证明避免了烦琐的计算,映射简洁优美,能够极大激发同学们的学习兴趣,唤起其对组合数学的热爱。而且证明的方式非常类似同学们小时候玩的积木堆叠,所用的工具唯一张纸而已,俯拾即是,同学们甚至可以动手去裁剪,去实验这个漂亮的映射。更进一步地,笔者还可以做如下延伸,让同学们思考如何利用表格组合证明下述公式:
当然讲解本部分知识时,笔者将联系黄金分割的概念、斐波那契数列与黄金分割之间的关系、黄金分割在美学中的应用等,让同学们进一步认识到组合数学在生活中的巨大作用,增加同学们选课的积极性。
结语
笔者认为通过上述教学设计可以由浅入深,由生活及课堂,借助日常工作生活中常见的表格循序渐进地引入组合数学,让同学们领略组合证明的魅力。综上,组合数学这门课程是非常有趣的,只要选择合适的教学内容、恰当的展开方式,辅以合理的教学设计,利用与组合数学相关知识的趣味性及应用性,一定能达到极佳的教学效果。

