基于卷积神经网络模型的医学图像融合

李雨晨，黄永东，2

1.北方民族大学 图像处理与理解研究所，银川 750021

2.大连民族大学 数学与信息科学研究中心，辽宁 大连 116600

医学图像融合是将相同或不同成像方式的多幅图像进行配准和整合，在保留特定特征信息的前提下提高成像质量的过程[1]。常用的解剖图像有CT图像和MRI图像，它们主要描述人体形态信息。由于CT图像对骨、钙化、早期脑出血等成像有很高的分辨率，而MRI能够很好地呈现神经系统、关节软骨、肌肉、脂肪和软组织病变。对CT图像和MRI图像进行融合能够有效降低图像信息的冗余性，提高医学图像诊断速度，给出综合有效的治疗方案，改进临床决策准确性[2]。

基于多尺度分解（MSD）的医学图像融合方法倍受学者的广泛关注并取得巨大成功，其主要步骤包括图像分解、特征融合以及图像重构。分解工具的选择对源图像信息是否能够充分提取有着十分重要的作用，常用的多尺度分解工具包含平移变化的分解工具和平移不变的分解工具。平移变化的分解工具有：金字塔变换、如拉普拉斯金字塔变换（LP）、梯度金字塔变换（GP）等；小波变换，如离散小波变换（DWT）、双树复小波变换（DTCWT）等；多尺度几何分析变换，如Curvelet变换以及Contourlet变换等。尽管基于上述变换的图像融合算法表现出了很好的性能，然而由于上述变换不具有平移不变性，因此在融合结果中存在伪Gibbs现象。平移不变的分解工具包括非下采样轮廓波变换（NSCT）[3]和非下采样剪切波变换（NSST）[4]，由于在分解和重建的过程中没有进行上下采样，因此具有平移不变性，可以较好地应用于图像融合中。但是基于NSCT和NSST变换的图像融合算法的计算复杂度相对较高，且在融合过程中没有充分的考虑空间一致性，可能会导致图像亮度或颜色的失真以及人工效应的出现。为了避免此类现象的发生，近年来，一些学者考虑到边缘保留滤波同时具有平移不变性和好的边缘保留性能，将其作为多尺度分解工具应用到图像融合领域并取得较为满意的融合效果，如引导滤波（GFF）[5]、梯度最小光滑滤波（GMSF）、局部拉普拉斯滤波（LLF）等。为了更好地根据图像的尺度信息来保留边缘信息，平滑图像的结构，基于滚动导向滤波（RGF）[6]的融合算法被提出，该算法具有良好的尺度感知性和边缘保护性，且在平滑图像同时实现降噪，相比于传统的MSD方法具有更好的性能。

利用多尺度分解得到的基础层主要包含图像的结构信息、能量信息和强度信息等图像数据信息。传统的基础层融合规则有绝对值取大[7]、绝对值平均、加权平均[8]、利用脉冲耦合神经网络或稀疏表示理论改进加权平均原则[9]和局部能量取大规则[10]等，这些融合规则都是手动设计的，有些规则还存在设计复杂问题，在一般情况下会造成图像数据信息不同程度的丢失。2017年，Liu等[11]基于CNN提出了一种新的多聚焦图像融合算法，该方法避免了手工设计权重系数问题，取得了非常满意的融合效果。受文献[11]启发，本文基于卷积神经网络提出了一种新的基础层融合规则，该规则能够更好地提取图像特征，并且融合图像能够很好继承源图像数据信息；能够直接得到更自然的融合图像，减少人工设计的痕迹。

细节层主要包含着图像的纹理信息和边缘信息，传统的细节层”绝对值取大”融合规则会造成源图像纹理信息或细节信息部分丢失，使得融合图像无法达到预期的效果。为了解决这个问题，本文利用绝对值取大规则和加权最小二乘法给出细节层的融合规则，通过调整不同样本误差对损失函数的贡献率，使得融合图像与源图像经过平滑后尽可能相似，尽可能保持源图像的边缘信息和纹理信息。

1 基础理论

1.1 滚动导向滤波（RGF）

滚动导向滤波是Zhang等[12]提出的一种新的边缘保留滤波。滚动导向滤波的实现过程简单、快速，在空间重叠特征中实现尺度的分离，所得结果没有出现人工效应。Zhao等在文献[13]中，对滚动导向滤波参数选取对图像融合结果影响进行了分析。

图1展示了一幅CT图像分别通过高斯滤波和RGF分解得到的细节层图像。可以看到，在图1（a）中，每一个细节层都包含边缘、轮廓及结构等信息。而在图1（b）中，（1）主要包含分散的细节信息，（2）主要包含CT图像的结构信息，（3）主要包含CT图像的强度信息，（4）主要包含轮廓信息及纹理信息。这说明RGF可以很好地保留不同类型的信息。

图1 滤波处理后的细节层Fig.1 Filtered detail layer

1.2 卷积神经网络（CNN）

卷积神经网络是指至少有一个中间层使用卷积运算的神经网络，是深度学习中的一种代表性网络模型。卷积操作使神经网络具有稀疏连接、参数共享等良好性质，相比于传统使用矩阵乘法的神经网络，极大缩小了模型的参数量和计算量，使网络模型具有有效特征学习能力。

近年来，卷积神经网络也被用于图像融合任务，Prabhakar等[14]首次将卷积神经网络应用于多曝光图像图像融合并提出了DeepFuse方法，取得非常满意的融合效果。Li等[15]将卷积神经网络应用于红外与可见光图像融合并提出了DenseFuse方法。Zhang等[16]提出的IFCNN应用于多聚焦图像融合，并将该网络扩展到医学图像融合和红外与可见光图像融合中，效果都有不错的改善。Liu等[11]提出的MFCNN能够提取多聚焦图像中清晰的部分生成聚焦权重图，极大地提高了多聚焦图像融合的能力。

图像融合的关键在于特征的提取和融合规则的设定[17]。而卷积神经网络能够自适应地从图像数据中提取特征，相较于传统手工设计方法，这种从数据中自适应地提取了特征更符合任务预期，鲁棒性更高。另外将图像融合规则与卷积神经网络结合起来，能够直接得到更自然的融合图像，减少人工设计的痕迹。

1.3 加权最小二乘法（WLS）

加权最小二乘法[18]是在普通最小二乘法的基础上对每个样本引入权重，调整不同样本误差对损失函数的贡献率，使之成为一个新的不存在异方差性的模型，然后采用普通最小二乘法估计其参数的一种数学优化技术。加权最小二乘法将输出图像视为输入图像尽可能模糊的版本，但保留了输入图像的显著梯度。换句话说，它是一种边缘保留滤波，它可以保存输入图像的突出边缘信息，表达式如下：

这里的u、g分别表示输出图像和输入图像，p表示像素的位置，λ是平衡两项的参数，a x,p和a y,p是依赖输入的相关矩阵的系数，有如下计算方法：

在此，l是输入的相关矩阵，α表示相关矩阵的梯度敏感度，ε是一个很小的常数，用于保证式（2）和式（3）可正常计算（通常设置为0.000 1）。

2 所提算法

本文首先采用由滚动导向滤波和高斯滤波组成的混合多尺度分解工具将CT和MRI图像分解为基础层和一系列细节层；其次用基于卷积神经网络的算法对基础层进行特征提取，进而得到一张与原图大小相同的权重图来进行基础层融合；结合绝对值取大规则和加权最小二乘法，对细节层进行融合，从而避免融合过程中合并过多不相关的细节和噪声。最后进行重构得到最终的融合图像。本文所提算法的流程图见图2。

图2 本文所提算法的流程图Fig.2 Flow chart of proposed algorithm

2.1 混合多尺度分解

高斯滤波在空间域和频率域上都十分有效，但是其忽视了边缘强度信息对滤波结果的影响，从而在图像融合中可能会导致不必要的边缘信息丢失。滚动导向滤波可以通过调控参数来达到保留图像边缘和平滑纹理的目的，其具有良好的尺度感知性和边缘保护性。文献[19-20]利用滚动导向滤波和高斯滤波相结合作为多尺度分解工具在多聚焦图像融合和红外与可见光图像融合上取得了很好的效果。基于上述思想，本文利用滚动导向滤波与高斯滤波相结合作为混合多尺度分解工具对医学图像进行分解。具体的混合多尺度分解公式如下：

这里u j表示第j层滤波图像，d j表示第j层的细节层，N为分解层数。图像u0等同于源图像I，基础层B由式（6）中的高斯滤波后得到，即为了获得更多的边缘信息和细节信息，参数σs在本文中设置较大，令

通过以上的多尺度分解方法，输入的源CT图像被分解为基础层B1和一系列细节层，MRI图像被分解为基础层B2和一系列细节层

2.2 基础层融合规则

传统的绝对值平均融合规则会导致基础层信息的丢失，从而导致融合图像的对比度降低。加权平均规则是基础层常用的融合规则，其方法简单，但这种手工设计权重系数的融合规则常常会丢失图像亮度、纹理、边缘、梯度、对比度等数据信息。受文献[11]启发，本文提出了一种基于卷积神经网络的基础层融合规则，有效避免了手工设计权重系数及信息丢失的问题。基础层融合规则如下：

步骤1使用预训练的双分支Siamese网络获取基础层B1、B2的初始权重图和。

双分支Siamese网络的框架结构示意图见图3，其由Liu等在文献[11]中提出的。该网络通过1 000 000个图像对进行训练，用来提取源图像的特征，并得到特征图。这些图像分别是高质量清晰图像和它对应的模糊图像，模糊图像是高质量清晰图像使用大小为7×7的高斯核模糊五次获得的，图像对中清晰的图像其标签为1，模糊的图像对应标签为0。将网络输出作为输入图像的初始权重。

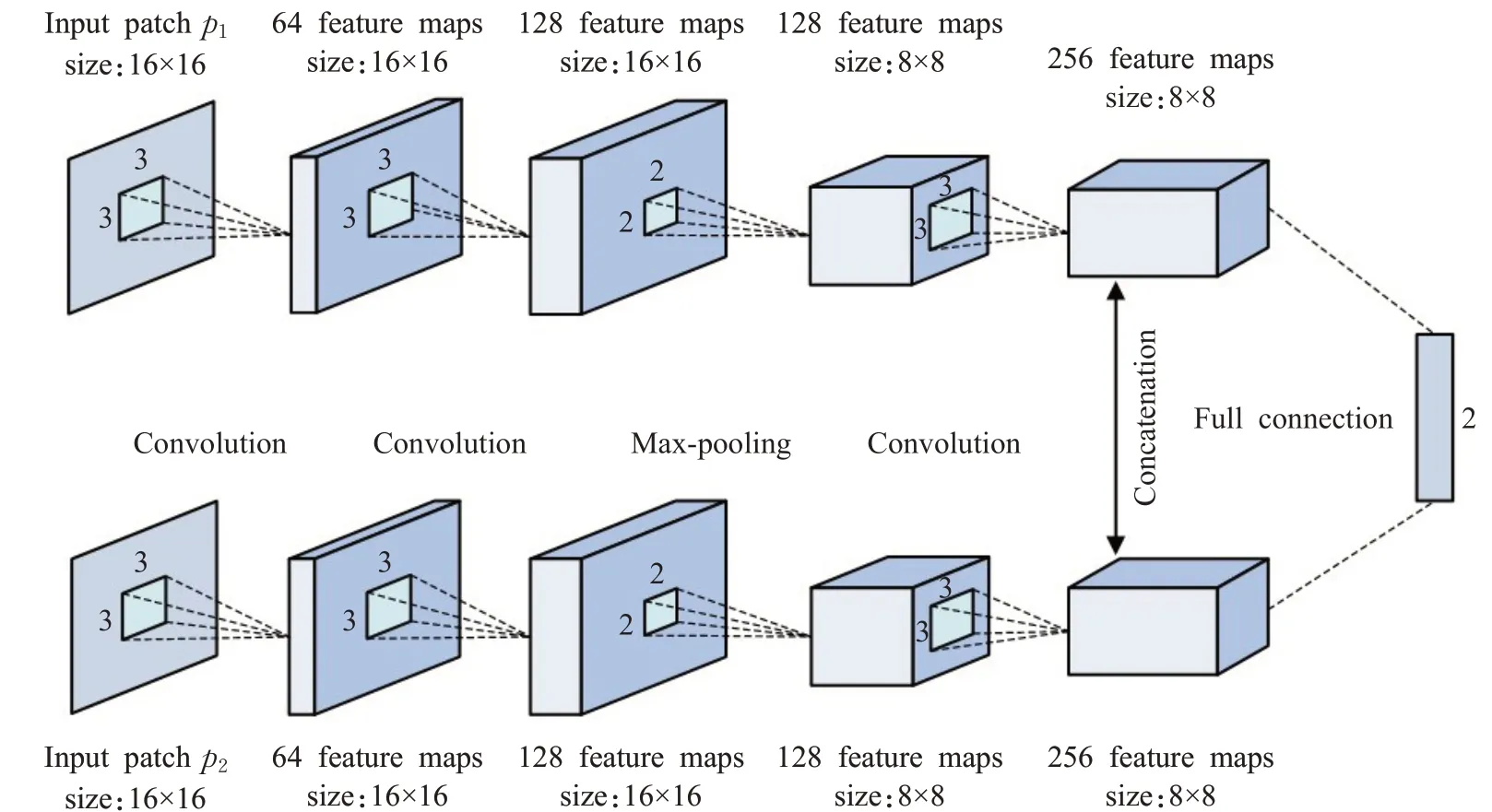
图3 双分支Siamese框架结构示意图Fig.3 Double branch Siamese frame structure diagram

步骤2通过平均重叠区域方法对初始权重图和W02进行处理，并得到与基础层图像B1和B2大小一致权重图的W11和W12。

由于卷积神经网络中包含池化操作，所以生成的初始化权重图W01和W02大小与基础层图像B1和B2大小不一致。为了便于操作，通过平均重叠区域将其恢复成和原始图像大小一致的权重图。

步骤3采用加权平均的融合规则对基础层图像B1和B2进行融合，得到融合后的基础层B F，即：

2.3 细节层融合规则

由于细节层主要包括图像的纹理信息和细节信息，且MRI图像中显示的软组织对比度较为明显，所以简单的细节层融合规则会导致源图像部分信息的丢失，为了避免在图像融合过程中合并过多不相关的细节和噪声，并尽量减少伪影的影响，利用以下步骤来进行细节层的融合：

步骤1通过绝对值取大规则计算权重矩阵W j：

其中，j=1,2,…,N。

步骤2使用高斯滤波处理权重矩阵W j，在式（9）中设置σs=2。

步骤3通过加权平均规则对细节层做初始融合得M j，即有：

步骤4使用优化策略WLS对M j进行优化得到融合后的细节层D j。具体过程如下：

将式（11）转换成矩阵形式：

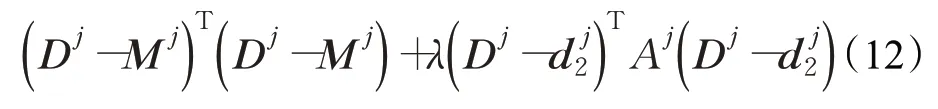
最小化式（12）得线性方程组：

由于A j=(A j)T，故式（13）可简化为：

利用式（14）可得融合后的细节层D j。

通过对CT图像中含有噪声或与视觉细节信息无关或与视觉细节信息相关区域分析可知，使用优化策略WLS能获得更好融合后的细节层。

2.4 图像重构

最后，融合图像F通过基础层融合结果B F和细节层融合结果D1,D2,…,D N相加得到：

3 实验分析

为了验证本文所提算法的有效性，选择CNN[11]、SR[9]、NSCT-SF-PCNN[21]、LAP[22]和NSCT[23]五种算法与本文所提算法进行比较，并选取了急性中风、致命性中风、脑膜瘤三类疾病的医学图像进行对比实验。本文所有实验图像来自哈佛大学医学院的全脑图谱数据库（The Whole Brain Atlas数据库）。算法运行环境是在3.6 GHz Intel Core i7-9700k-CPU，8 GB（RAM），R2018a MATLAB的主机上完成。

3.1 融合规则可行性分析

为了验证本文所提算法基础层融合规则和细节层融合规则的有效性，本文选取了20组CT-MRI医学图像进行了实验。在此部分实验中，RGF和GF组成联合滤波器作为所有算法分解和重构的工具。标准偏差（STD）用来度量图像的对比度，值越大说明融合图像中包含的细节信息越丰富。Method1是指基础层使用局部能量取大，细节层使用本文所提细节层融合方法。Method2是指基础层使用本文所提基础层融合方法，细节层采用能量平均方法。Method3是指基础层和细节层分别使用局部能量取大和能量平均的方法，以及本文所提方法。表1是四种融合方法应用到20组实验图像后获得的融合图像标准偏差（STD）指标的平均值。

表1 不同融合方法的标准偏差（STD）的平均值Table 1 Mean values of STD for different fusion methods

从表1中可以清晰地观察到，本文算法具有最优的指标，即有着最好的融合效果。

3.2 主观分析

为了说明本文所提算法视觉效果有效性，从急性中风、致命性中风、脑膜瘤三类疾病实验图像中随机选取了这三类疾病各两组图像，应用本文所提算法和五种对比算法获得相应的融合图像，给出两组实验结果。对于CT与MRI图像来讲，判断融合图像视觉效果的优劣主要考虑两个方面，一是MRI图像提供的结构细节信息被尽可能完全的融合，二是CT图像所提供的边缘亮度信息得到有效的应用。

图4为急性中风疾病的CT与MRI源图像和不同算法融合图像的对比图，给出了两组图片的实验对比结果。从图4可以观察到，CNN算法的融合图像内部丢失了MRI图像的结构细节信息；LAP、NSCT、NSST-SFPCNN算法的融合图像中源CT图像的边缘信息亮度较低，对比度也不如本文所提算法；SR算法的融合图像在图像内部及边缘部分产生了明显的失真现象；本文所提算法的融合图像在保存源图像边缘和全局对比度方面都具有更好的效果。

图4 急性中风源图像与不同算法融合图像对比图Fig.4 Comparison of source images and fusion images on acute stroke

图5为致命性中风疾病的CT与MRI源图像和不同算法融合图像的对比图，给出了两组图片的实验对比结果。从图5可以看出，NSST-SF-PCNN与SR算法的融合图像中同样存在着边缘信息丢失（如红色方框中所示）的现象；LAP、NSCT算法的融合图像强度信息较低；CNN算法与本文所提算法的融合图像都能很好地保存结构信息和强度信息，但本文算法对比度更加清晰。

图5 致命性中风源图像与不同算法融合图像对比图Fig.5 Comparison of source images and fusion images on fatal stroke

图6为脑膜瘤疾病的CT与MRI源图像和不同算法融合图像的对比图，给出了两组图片的实验对比结果。通过比较源图像和对比图，可以观察到，CNN算法的融合结果纹理细节信息不清晰，在图像内部可以观察到对MRI源图像所提取的信息不够；SR算法融合图像有着严重的融合结果失真情况，在边缘处（如红色方框内）可以看到明显的结构信息丢失的现象；LAP算法的融合图像对结构信息的保留较为完好，可是在边缘上（如红色方框内）可以非常清晰地观察到有丢失边缘信息的情况；NSCT-SF-PCNN算法的融合图像没有很好地保存MRI图像的信息，并且在边缘处存在人工伪影（如红色方框内）的现象；NSCT算法的融合图像整体亮度较低，且在边缘处信息丢失较为严重，不符合人眼的视觉感知规律。而本文算法对比度清晰，对边缘部分和结构信息的保留更加完善，且更加符合人眼感知规律。

图6 脑膜瘤源图像与不同算法融合图像对比图Fig.6 Comparison of source images and fusion images on meningioma

3.3 客观分析

为了客观评价本文算法的有效性，选取以下四种指标为客观评价指标，边缘强度（EI）、互信息（MI）、空间频率（SF）和标准偏差（STD）。

3.3.1 客观评价指标

边缘强度（EI）代表图像边缘锐化程度，值越大代表融合图像质量越好。

互信息（MI）反映了融合图像中有多少信息来源于源图像，互信息值越大，融合效果越好。

空间频率（SF）反映的是图像在空域的梯度分布，度量图像细节信息的丰富程度，值越大代表图像细节越清晰。

标准偏差（STD）主要用于度量图像信息的丰富程度，反应了图像灰度相对于平均灰度的离散情况，值越大表明图像的细节信息越丰富。具体计算公式可参考文献[11]。

3.3.2 客观评价

表2是60组CT-MRI图像通过六种方法获得的融合结果图的客观评价指标平均值，表中黑体加粗表示最优值，下划线数值表示次优值。从表2可以看出，本文所提算法在SF和STD这两个指标是最优的，这是由于本文算法通过卷积神经网络进行特征提取，并利用边缘保护滤波对边缘进行保护，所以融合图像具有更清晰的梯度信息和更丰富的细节信息。而SF和STD最能体现本文算法在此方面的优越性。此外，SR算法的EI指标比本文提出算法略好，但是通过观察融合图像，如图4～图6可以发现，SR算法的融合图像具有严重的边缘模糊现象，与客观指标不符。本文所提算法MI指标在致命性中风和脑膜瘤疾病图像中排在第二位，在致命性中风疾病图像中仅次于NSCT算法结果，在脑膜瘤疾病图像中次于NSCT和LAP算法结果，这个问题产生的原因是本文使用了加权最小二乘法优化了源图像信息，但是NSCT和LAP算法的融合结果图与本文算法相比在边缘处存在着模糊和细节信息丢失的情况，视觉效果明显不如本文所提算法。而在急性中风疾病图像中，本文所提算法的MI指标为第一名。所以综合主客观分析，本文所提算法具有更优越的性能。因此，尽管本文算法个别指标数据结果不是最优的，但是综合主观评价和客观评价，本文所提算法融合图像是最优的。

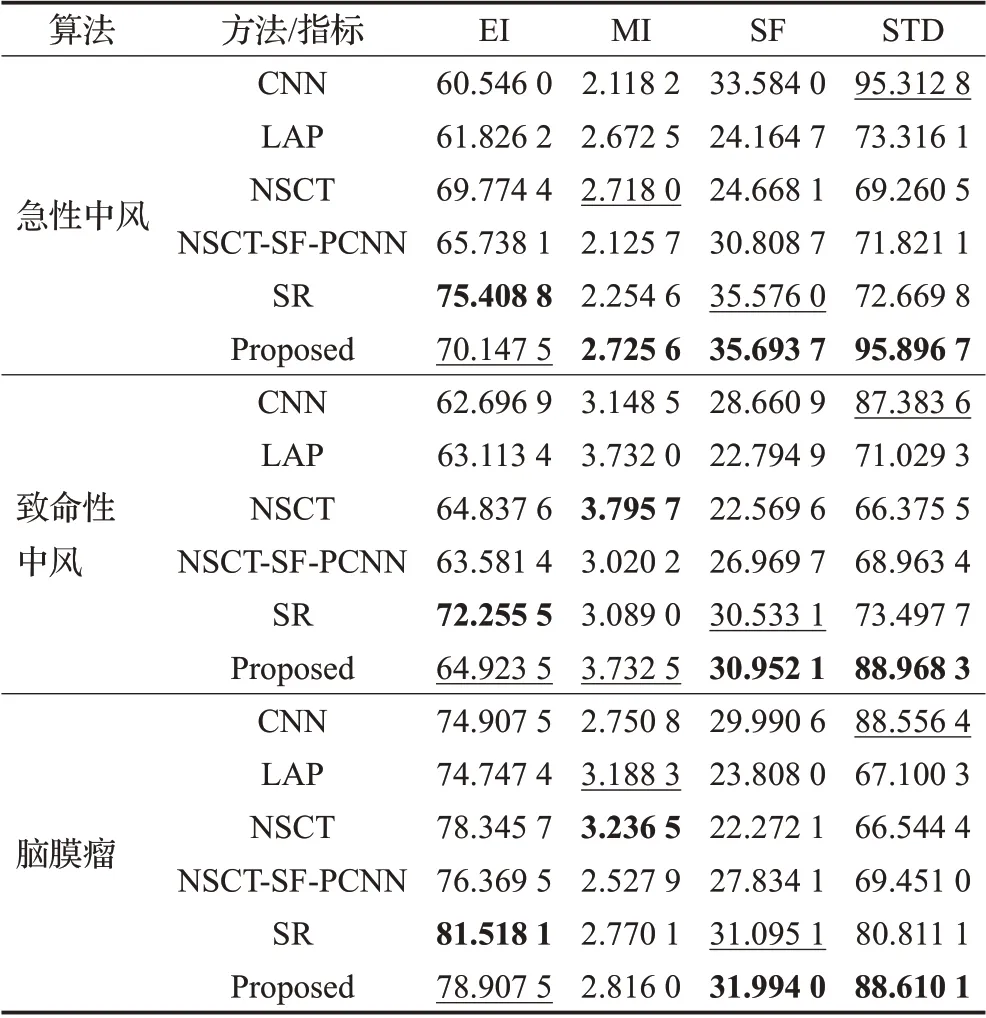
表2 六种算法客观评价指标平均值Table 2 Mean values of objective evaluation index of six algorithms

图7是60组MRI图像与CT图像使用不同算法获得的融合图像的客观评价指标平均值的柱状图，用来综合评价本文所提算法与其他算法的优劣。从图7中可观察到，本文所提算法的指标平均值在SF和STD指标上是最优的，这两指标代表着本文所提算法有更清晰的细节，更锐化的边缘和更明晰的梯度分布。此外，本文所提算法仅在EI指标上逊于SR算法，MI指标逊于LAP和NSCT算法，这是由于本文所提算法优化了源图像信息造成的。

图7 融合图像客观指标平均值柱状图Fig.7 Histogram of mean value of objective index

为了更直观地分析本文方法在客观指标上的优越性，图8使用了折线统计图进一步分析客观评价指标。图8（a）中本文方法在脑膜瘤疾病图像中EI值较大，说明本文所提方法在这一类疾病图像的细节清晰度和边缘锐化度较高。图8（b）中本文方法在致命性中风中MI值较大，说明本文所提方法在这一类疾病图像包含的源图像细节信息更多。图8（c）中本文所提方法在急性中风疾病图像中SF值较大，证明本文算法在这一类疾病图像的梯度值较高，度量图像信息更丰富。图8（d）中本文所提方法在三类疾病图像效果持平，每一类疾病图像都具有较高的对比度，因此，本文所提方法可以尽可能多地融合源图像信息，且融合效果更好。

图8 三种疾病不同客观指标折线图Fig.8 Line plots of different objective indicators on three diseases

3.4 算法复杂度分析

表3是本文所使用的6种方法用于医学图像融合的时间比较，从表中可以看出，本文算法所用时间与NSCT、LAP、SR方法相比较长，这主要是因为CNN比较耗时，但是CNN能很好地提取源图像中特征信息。所以说，为了得到更好的融合效果，时间代价是值得付出的。

表3 不同融合算法的运行时间Table 3 Running time of different fusion algorithms

综上所述，与经典的融合规则和现有的一些医学图像融合算法相比，本文所提医学图像融合算法在主观评价和客观指标方面都有一定的优势。

3.5 讨论

本文所提算法主要针对解剖医学图像的融合方法进行了研究，并且取得了很好的融合效果。但是由于卷积神经网络没有针对医学图像进行训练，所以即便具备良好的特征提取能力，仍要进一步针对医学图像设计卷积神经网络模型。因此，下一步工作重点是对卷积神经网络进行进一步的优化，并寻找或设计适用于多种类型医学图像的融合算法。

4 总结

本文考虑到多模态医学图像的不同成像特点，为了避免边缘信息和结构信息的丢失，选取了具有保护边缘能力的滚动导向滤波（RGF）和高斯滤波（GF）构成的混合多尺度分解工具分解医学图像，使得分解过程中边缘信息能够得到很好的保存和增强。其次，基于卷积神经网络本文提出了一种新的基础层融合规则，联合绝对值取大规则和加权最小二乘法给出细节层融合规则。最后，通过仿真实验表明本文算法具有较好优势。