基于LSCP算法的比特币网络异常交易检测

廖 茜，顾益军

中国人民公安大学 信息网络安全学院，北京 102600

作为区块链技术最具代表性的应用，比特币是近十年在数字货币投资领域和研究领域最热门的话题之一。依托加密算法、POW共识机制和P2P分布式网络技术，比特币具有去中心化、分散化、匿名性、总体运营安全等特点。正是基于这些特性，加之数字资产监管法律规制的不健全，比特币被众多不法分子利用，导致了暗网交易[1]、勒索诈骗[2-3]、洗钱[4]等一系列网络、金融犯罪。2017年频繁爆发的全球性比特币勒索案件就是被不法分子利用的典型[5]。因此，分析交易数据、研究比特币网络异常交易的检测方法对于公安机关和有关监管部门规范交易行为、保障网络空间安全、强化金融治理具有迫切的现实意义。

1 相关工作

异常检测是数据挖掘领域研究的一个重要问题，机器学习的发展为挖掘异常交易提供了广阔的思路。比特币系统中的异常被研究者们定义为不正常或不太可能的可疑情况[6]，如勒索诈骗、黑客攻击、暗网交易等。当前，学术界的异常交易检测工作普遍是依托交易数据构建的网络结构对交易节点提取异常行为模式相关特征，构建多维特征向量，再运用机器学习的方式加以检测。斯坦福大学的有关学者早在2013年就开始了采用机器学习技术对公开可用的比特币交易数据加以深入探究，其中Hirshman等人[7]针对比特币系统中的洗钱和“混币”服务，在使用Kmeans聚类方法对用户初步分析后提出基于结构特征相似性的无监督算法RoIX将节点进一步角色分类。由于缺乏数据标签，作者的研究虽然在追踪“混币”服务方面效果不佳，却发现各聚类中心存在一定的异常交易行为，为进一步发现交易数据中的异常模式奠定了基础。Pham等人[8]在交易图和用户图上尝试使用LOF算法构建检测模型，论文根据幂率分布初步确定了比特币系统中存在异常用户。然后利用LOF算法进一步细化定位到存在的异常用户；Monamo等人[9]在文献[8]基础上尝试了在聚类的同时可以实现异常检测的算法trimmed-Kmeans，实验结果表明，在相同的研究条件下，trimmed-Kmeans更具优势；由于trimmed-Kmeans是基于全局的异常检测算法，Monamo等人[10]在文献[9]的基础上引入基于近邻的异常检测算法kd-trees，对比两类算法的检测效果；沈蒙等人[11]以分析交易动机为切入点，设计了两类典型异常交易行为的判定规则并利用子图匹配技术实现了比特币异常交易行为识别算法。曾雅倩[12]利用Elliptic公司公开的比特币交易数据，基于交易实体的多维特征和交易流构建半监督分类模型图卷积神经网络，为探究比特币反洗钱监测模型提供了建模思路。Omer[13]利用比特币客户端提供的原始数据创建数据集，并使用IForest、CBLOF等5种经典的无监督检测算法分析恶意交易。论文首次采用集成学习的思想建模，将多种异构基学习器在简单平均策略下并行集成。对比单一的检测方式，集成学习方法在AUC值等综合检测性能方面显示了出众的效果。

综上所述，由于交易数据量大、无实体认证导致获取尽可能多的用户标签困难，现有研究多从传统的无监督学习视角出发，集成学习的应用仅限于将异构基学习器并行叠加最后以简单平均策略输出结果。集成学习作为近年来机器学习领域的研究热点，已有很多学者将集成学习运用于异常检测[14-15]，以提高模型的检测能力。由于数据在高维空间分布较为稀疏，无关特征的存在会干扰异常检测的效果，Lazarevic等人[16]提出了最早的集成异常检测框架feature bagging。类似于随机森林算法，feature bagging通过从原始特征集中抽取特征子集来训练多个基学习器，并最终采用一定的策略组合所有的基学习器以提高模型对高维数据的整体检测性能。Aggarwal等人[17]在集成分析广泛应用于高维数据离群点检测的基础上探究了集成异常检测的理论基础——偏方差理论。同时，作者提出了两种新的基学习器平衡组合策略：AOM、Threshold-Sum以达到在集成系统中权衡方差与偏差的效果。由于为了增加学习器的多样性而不加选择地组合准确性较低的基学习器可能会降低集成方法的整体性能，Rayana等人[18]提出顺序集成方法SELECT对异构基学习器选择性地组合，相比于比非选择性集成算法更具可靠性和稳定性。为了进一步平衡集成学习系统的多样性和准确性，Campos等人[19]首次将有监督的提升方法boosting应用到无监督集成异常检测场景中。因为缺乏数据标签，boosting方法在异常检测中应用较少，现有研究基于bagging和feature bagging方法对基学习器并行集成较多。然而现有的并行集成方法缺乏选择性地组合基学习器导致表现优异的基学习器难以发挥优势，组合之后的模型只能达到较为一般的效果。同时，现有的大部分算法是以全局的角度出发，较少细致地关注数据的局部性。针对这两方面的问题，Zhao等人[20]提出基于局部动态选择组合的并行集成异常检测算法（locally selective combination in parallel outlier ensemble，LSCP），采用局部异常因子算法LOF并设置不同超参数以实现基学习器的多样性，通过定义局部区域和伪标签生成方式为每个数据点选择邻域空间中表现最佳的基学习器作为最终结果输出。对比传统的基学习器合并策略，LSCP算法达到了权衡方差与偏差的效果，表现出更好的泛化能力。

鉴于LSCP算法在集成过程中考虑了“动态选择”和“局部性”，本文借助LSCP算法进行比特币网络异常交易检测。针对LSCP算法为实现系统多样性采用的是对同构基学习器设置不同的超参数的方法，未曾尝试在系统中使用异构的基学习器。一般而言，大规模数据往往存在多种类型的异常点，为提高集成学习的检测性能，要求基学习器应“好而不同”[21]。单一的LOF算法通过计算每个样本相对于其周围样本点的相对密度来度量异常程度，对全局异常点的检测效果较差，而且对稀疏分布下的异常簇不敏感。为此，本文在LSCP算法中融入LOF算法、经典的KNN算法和文献[13]中采用的5种无监督异常检测算法，利用异构基学习器对不同异常类型的敏感性，提升检测模型的整体性能。实验结果表明，与单一的检测算法和简单平均策略的集成方法相比，本文方法在比特币异常交易检测任务中具有更好的综合性能。

2 基于LSCP的比特币异常交易检测方法

2.1 原理介绍

目前将集成学习应用到异常检测领域通常是将若干个基学习器并行叠加，然后将多个基学习器的结果以投票法、均值法等结合策略输出，这些结合策略未对基学习器加以选择，导致表现优异的基学习器检测能力被掩盖，性能较差的基学习器对整体性能的影响较大，互补性不足。同时，基学习器的结合策略一般是从全局角度出发，而强调数据的局部性可以使检测结果更加精确、细致。LSCP算法的基本思想是：对一个数据点的异常程度进行预测时，先定位到该点的局部区域，利用伪标签对所有基学习器在局部区域的表现加以评估，最后选择在局部区域具有优异表现的基学习器进行二次合并作为该点的输出结果。虽然异常检测与有标签的分类问题有差异，Aggarwal等人[17]证明偏差-方差理论同样适用于集成异常检测领域。从偏差-方差理论的角度出发，LSCP算法根据局部区域动态地为每个数据点挑选最佳的基学习器，能够达到降低整体偏差的效果；而基学习器的多样性和根据伪标签的评估情况二次合并多个最优基学习器作为最终结果，可以降低系统方差，减小对数据变化的敏感性。因此，LSCP算法对异常数据的检测具有良好的泛化性能和准确性。

现有的无监督异常检测算法大致可分为以下主要几类：（1）基于最近邻的技术；（2）基于聚类的方法；（3）基于统计的方法；（4）基于子空间技术；（5）基于模型的方法。针对大规模数据异常类型的多样化，为了借助异构基学习器增加集成系统的多样性和对不同异常类型的敏感性，并与文献[13]进行效果比对，本文在LSCP算法中融入上述5种研究视角的7种经典的无监督异常检测算法，如表1所示。

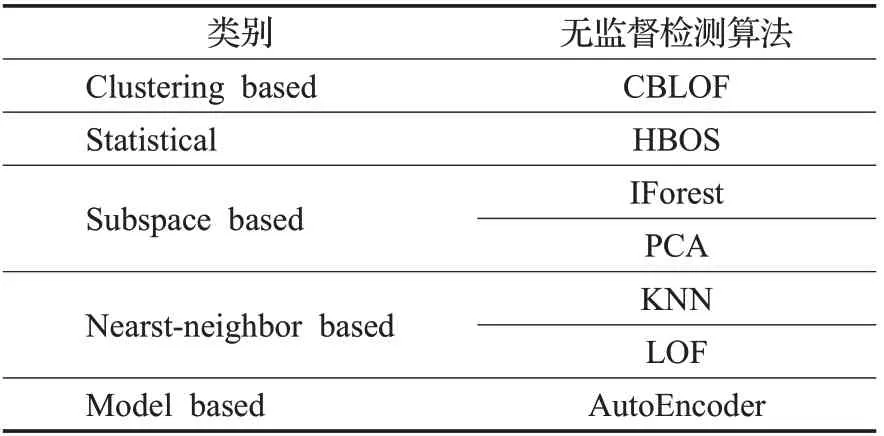
表1 异构基学习器的具体算法Table 1 Specific algorithm of heterogeneous learner

2.2 实现步骤

为实现比特币网络异常交易的更有效检测，本文采用融合异构基学习器的LSCP算法，算法1为LSCP算法的伪代码，具体实现步骤如下：

算法1LSCP算法

输入：训练集Xtrain∈Rn×d；测试集Xtest∈Rm×d；

r个异构基学习器；t为特征子集的个数；

k为局部区域内满足条件的训练样本数。

输出：Xtest的异常分数。

1.利用训练集Xtrain分别训练r个异构基学习器，将结果合并为异常分数矩阵O(Xtrain)

2.生成Xtrain的伪标签target

3.forinXtestdo

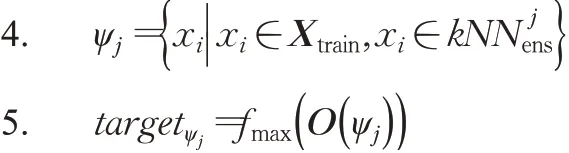
6. forT rinTdo

9. end for

10. 最相似的前x个基学习器T*x

12.end for

（1）训练多个异构基学习器。具体的，对比特币交易数据集采用留出法划分训练集与测试集，Xtrain∈Rn×d表示由n个点、d维特征向量的训练数据构成的特征矩阵，Xtest∈Rm×d表示由m个点、d维特征向量的测试数据构成的特征矩阵。LSCP算法首先借助一定参数设置下的r个异构基学习器训练数据，产生异常分数集T={T1,T2,…,T r}。其中，T r(·)表示第r个基学习器对交易数据点的异常分数向量。异构基学习器对训练数据进行异常评分并Z-score标准化后的异常分数矩阵表示为O(Xtrain)。

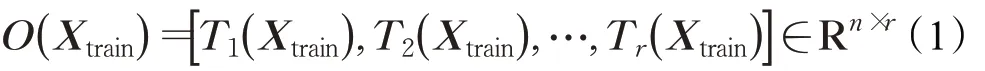
（2）定义伪标签生成方式。为了在缺乏数据标签的情况下采用伪标签评估基学习器的检测能力，本文采用所有基学习器输出结果的最大值作为交易数据点的伪标签，最大程度地保留数据点的异常特性。即：

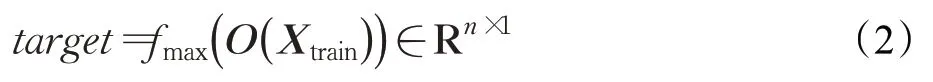
（3）定义局部区域。为了从数据的局部性出发到达更加细致的检测效果，算法对一个新数据点检测时，先对所有基学习器在这个点邻域空间的表现进行评估，并认为基学习器相应地在这个点也会有同样的表现。因此，为了确定数据点的邻域空间需要对局部区域加以定义。将测试数据点的局部区域ψj定义为k个最近训练数据点的集合。k值并不固定，取决于满足条件的训练样本的数量。类似于Feature bagging思想，为减少高维空间中不相关特征的干扰并降低计算复杂度，采用特征子集挑选满足条件的训练样本点。具体实现如下：

①随机选择t组维度范围为的特征子空间。

②对于每一组特征子空间，通过计算欧氏距离在训练集中获取与最近的k个训练样本点。

③将步骤②中出现次数超过的样本作为的局部区域ψj。

（4）得到测试数据点的局部区域后ψj，利用训练好的基学习器生成该局部区域的异常分数矩阵

（5）得到局部区域ψj的数据点的伪标签，生成目标向量targetψj，即：

（6）为了选择在数据点上表现优异的基学习器，计算异常分数矩阵O(ψj)的每个列向量和目标向量targetψj之间的皮尔逊相关系数，选择与目标向量最相似的前x个基学习器。

（7）最后进行基学习器二次选择组合，根据选择的x个基学习器，计算测试数据的异常分数，将x个异常分数的平均值作为的最终异常分数，以降低伪标签定义方式带来的随机性和方差，提升算法的可靠性。具体实现流程如图1所示，其中浅色区域可以通过缓存读取，深色区域需要重新计算。

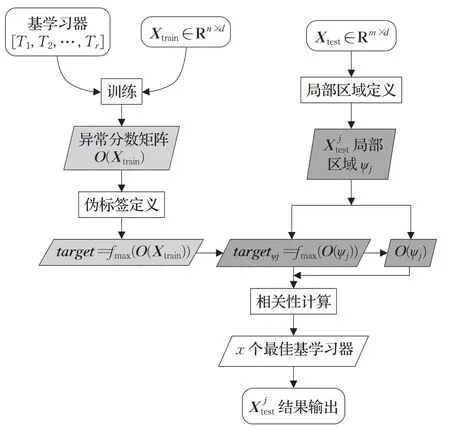
图1 基于LSCP算法的比特币异常交易检测流程Fig.1 Bitcoin abnormal transaction detection process based on LSCP algorithm

3 实验分析

3.1 数据集与特征提取

本文使用比特币公开交易数据进行实验研究。该数据集由Omer（https://ieee-dataport.org/open-access/bitcoin-transactions-data-2011-2013）公布，从bitcoin core客户端的blk.dat文件提取而来，包含了2011年至2013年的交易流信息，具体字段说明如表2所示。在现有比特币相关研究领域，由于缺乏完整的标签信息，大多以半手工方式标注数据集。比特币权威论坛Bitcoin Forum（https://bitcointalk.org/index.php?topic=576337）公布了2011年至2013年期间的历史非法交易，其涵盖了BTC盗窃、BTC黑客攻击和BTC丢失等各类案件的详细信息，包括涉案金额、日期、交易ID等。本文借助Python编写的爬虫在该论坛对非法交易进行采集，并借鉴文献[22]的方式将非法交易及其子交易标注为异常（1），其余交易则标注为正常（0）。经统计，数据集中包含108个异常类，30 248 026个正常类，异常类的比例约为0.000 35%。

表2 特征说明表Table 2 Feature list

利用交易流信息，本文使用python-igraph包（版本0.7.0）构建以交易为节点的有向无环网络图，并在此基础上提取7种有代表性的节点异常行为模式相关特征：

（1）交易网络特征：入度、出度。

（2）交易资金特征：总接收数额、总发送数额、平均接收数额、平均发送数额、净余数额。

3.2 实验步骤

为验证本文方法的优越性，本文将组成异构基学习器的各无监督检测算法、上述异构基学习器在简单平均策略下并行集成的检测方法（Avg-Ensemble）作为实验对照组。实验在Windows 10系统、3.0 GHz Inter Core i5处理器、Python3.6.3环境下运行，步骤如下：

（1）读入数据并进行预处理。读入数据，检查数据的格式、查看数据的分布情况。针对提取的各交易特征具有较高的偏度和峰度值，实验过程中使用对数变换对各数据特征进行转换，降低较高的偏度和峰度值对后续建模分析产生的不利影响。在此基础上，本文采用更适用于处理有异常值的稳健标准化方法对交易数据的多维特征标准化。

（2）考虑到数据整体规模较大且样本类别分布不平衡程度较为严重，本文对正常类交易进行简单随机抽样，与所有异常类样本构成正负比例为1∶500的新数据集，以在保证实验合理性的同时减少计算开销。为避免随机因素影响、降低抽样误差，简单随机抽样20次以构造20个子数据集，最终以实验平均值反映检测效果。图2为数据分割示意图。

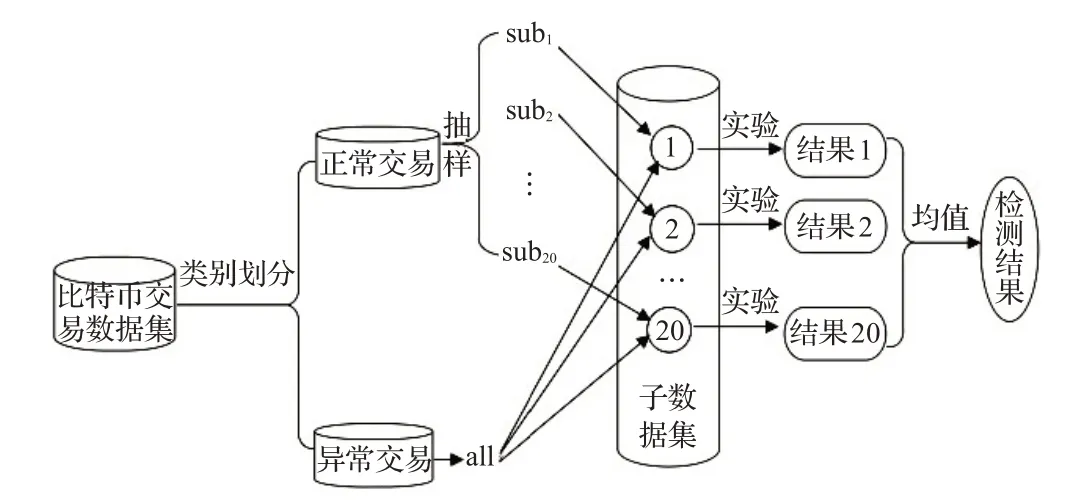
图2 数据分割示意图Fig.2 Data segmentation diagram

（3）将每个子数据集采用留出法以7∶3的比例划分训练集、测试集，划分时对正负类别的样本进行随机分层取样，确保训练集、测试集中各类样本分布与子数据集相同。

（4）为避免子数据集类别不平衡影响检测性能，采用SMOTE算法在训练集上对少数类样本即异常交易进行过采样，最佳采样比作为实验参数进行调优。

（5）在各子数据集的训练集中利用各算法迭代训练模型，采用Hyperopt超参数优化技术以最大化AUC值为目标函数进行逐步调参，选取最优参数组。

（6）利用最优参数训练而成的模型在测试集中依据异常分数阈值预测各交易点的分类结果。

（7）由于数据集高度不均衡，并且在公安实战中与正常行为相比更关注异常突发状况，与整体预测效果相比更关注预警、处理的及时性，因此本文选取AUC值、召回率Recall、检测结果的前n项的准确率Precision@k作为泛化性能评估指标。这些评估指标在异常检测领域也得到广泛使用[15，23]。依据测试集的分类结果计算各评估指标值，最终检测效果由20个子数据集计算平均值得到。

3.3 实验结果对比与分析

20个子数据集上的AUC值、召回率Recall、Precision@k结果如表3所示。综合表3可知，在各评估指标上，每个算法在不同的子数据集中表现趋于稳定，没有严重的波动情况，这说明了在大规模的数据集中对正样本多次抽样并未造成数据分布的较大差异，由数据抽样而造成的误差程度较小。

由表3可以看出，对比所有单一的检测算法，LOF、KNN和PCA在三个评估指标中均表现不佳，HBOS、CBLOF和AutoEncoder表现能力相当且较为出色。原因可能是，KNN和LOF均是基于近邻的算法，KNN认为异常点的K近邻距离更大，LOF算法利用K近邻的距离将异常值建模为邻域密度相关的函数。而在子数据集训练前期，SMOTE算法通过线性插值的方式在两个少数类样本之间生成新的样本，这种数据生成方式一定程度上改变了数据集的原始分布，从而导致基于近邻的思想对异常样本的敏感性降低。PCA和AutoEncoder均是基于重构误差来定义数据的异常程度，但是Auto-Encoder在使用非线性激活函数时克服了PCA线性的限制，可以学习到更为复杂的数据投影，因此AutoEncoder相比于PCA具有更加优异的表现。

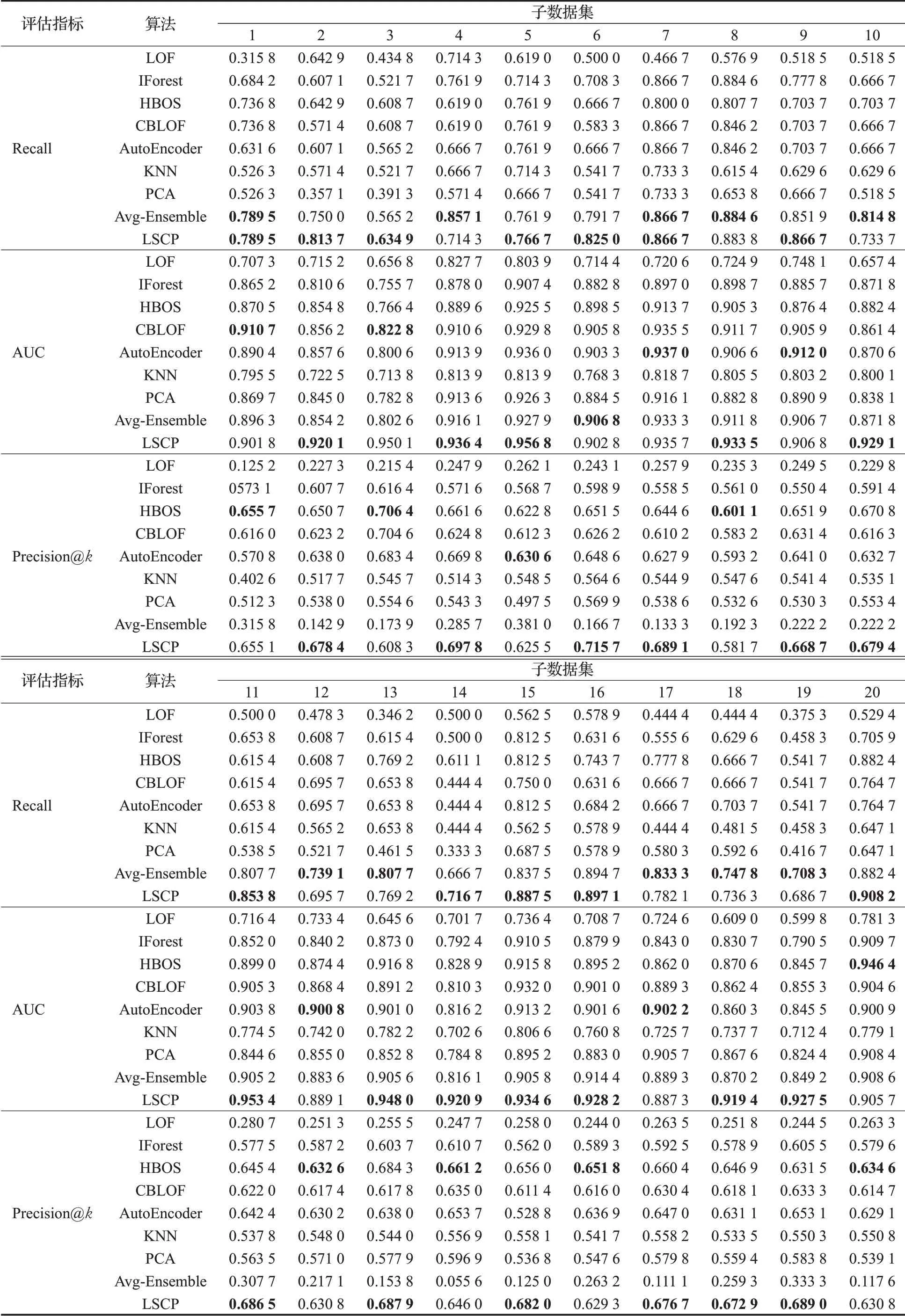
表3 LSCP与基准算法对比结果Table 3 Comparison results between LSCP and benchmark algorithms

由于在异常检测领域，与将所有数据点进行单纯的二分类相比更在乎排序结果中异常值最高的K个点是不是更异常，所以本文选取Precision@k作为重要的评价指标。由图所示，从大多子数据集可以看出，Avg-Ensemble虽然在召回率上具有一定优势，AUC值上也有较好的表现，但是在Precision@k指标上却处于最低水平。这说明，Avg-Ensemble虽然能将大部分异常交易正确分类，却不能将它们置于靠前的异常排名中以尽早发现加以处理，其对异常交易的检测能力有待提升，以达到更加精准、细致的效果。对比融入异构基学习器的LSCP算法和其他算法在三个评价指标中的值可以看出，LSCP算法即使在没有处于最高水平的情况中也与最高水平相差不大。虽然并不总是优于其他方法，但是整体性能优于其他方法，对异常比特币交易的检测具有较好的可靠性和稳定性。为了避免抽样误差对实验结果造成的影响，本文对各算法在20个子数据集中的表现计算平均值以得到最终的检测效果。各算法在三个评估指标中的平均值如图3所示。

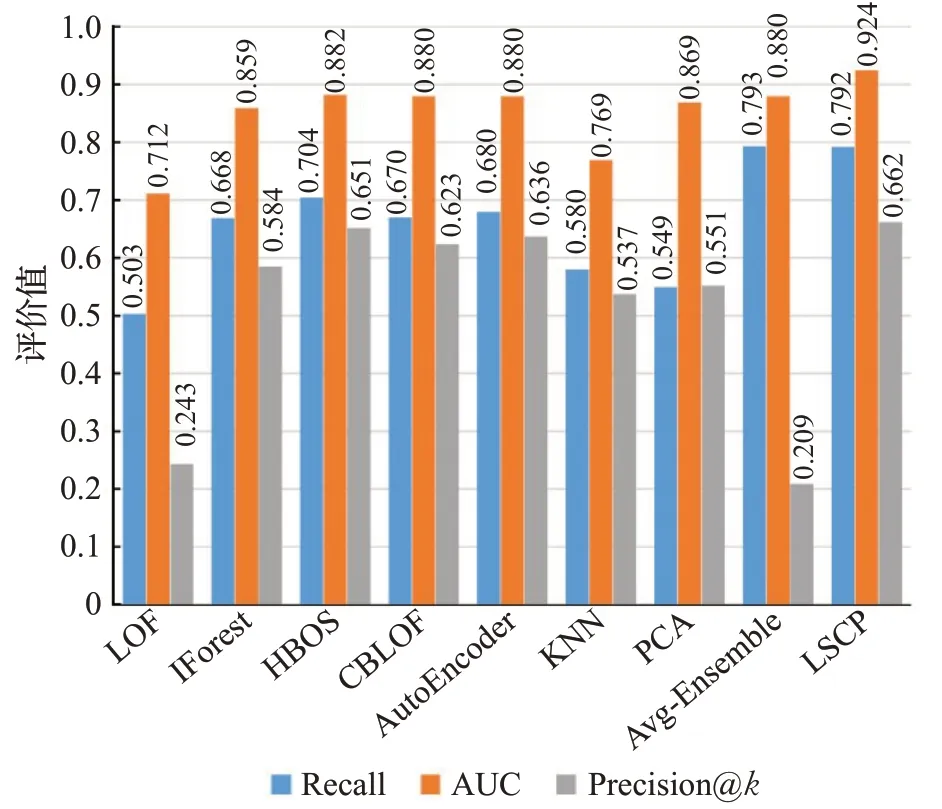
图3 LSCP与基准算法综合效果对比Fig.3 Comprehensive effect of LSCP and benchmark comparison method

由图3显示，Avg-Ensemble虽然在召回率上具有出众水平，但在AUC值上与表现最佳的单一检测算法HBOS水平相当，且在Precision@k方面表现最差，未能达到理想的检测效果。融入异构基学习器的LSCP算法对异常交易的总体检测召回率与Avg-Ensemble相差不大，比单一的检测算法提升了至少9个百分点。在AUC指标方面，LSCP方法比次优算法HBOS提高了约4个百分点。同时，LSCP方法在Precision@k上比次优算法HBOS提升了约1个百分点。实验结果表明，LSCP算法对异常比特币交易检测的综合能力比其余基准算法出色，具有良好的泛化性能。这证明，LSCP方法由于在集成系统中考虑了局部性的概念并针对大规模数据多样的异常类型充分利用异构基学习器对不同异常类型的敏感性，在最终的选择过程中对不同的交易数据点

动态性选择表现优异的基学习器，因此解决了不同算法在特定异常类型上的局限性，进一步提升了集成学习的优势。

4 结束语

本文将LSCP算法应用于比特币网络异常交易检测，并在LSCP算法中融入了近邻、聚类、深度学习等目前在该领域常用的算法思想，以提升对不同异常类型的敏感程度，达到动态选择和局部细致的效果。结果表明，本文方法在AUC值、召回率Recall、Precision@k上整体优于基准算法，具有优异的综合性能，在公安工作中具有重要的实际意义。事实上，本文方法在为数据点确定局部区域的过程中需要较长时间，今后的研究可以考虑优化局部区域定义方法，以加快在大规模比特币交易数据中的检测速度。