基于滑模控制的永磁同步电机模糊调速系统*

陈国真, 田亚南

(中国电子科技集团公司第五十八研究所，江苏 无锡 214072)

0 引 言

永磁同步电机(PMSM)具有功率密度高、可靠性好、体积小等优点，在航空航天、特种加工、新能源汽车等领域得到了广泛的应用[1-3]。然而，由于PMSM多变量、强耦合、参数摄动等非线性因素的影响，使用传统的PID控制策略已无法取得较好的动态响应性能。

滑模控制对电机的参数摄动和外部干扰具有较好的鲁棒性，且实现简单，广泛应用于PMSM的控制系统[4-7]。为提高系统的动态响应性能，需加大滑模控制器的切换增益。然而，切换增益太大会导致系统抖振增加，从而严重影响系统的稳态误差，甚至有可能激发未建模高频模态而造成系统的破坏。模糊控制可根据系统输入实时调整控制系统的参数，因此，将模糊控制和滑模控制结合，可以有效地解决系统动态响应性能和抖振之间的矛盾。文献[8-10]将速度误差和其变化率作为模糊控制器的输入变量来实现滑模控制器参数的调整，文献[11-13]将滑模面及其导数作为输入变量。文献[8-13]的模糊控制器采用双输入变量会增加模糊规则的复杂性，输入项含有导数会增大系统噪声并导致控制器的缩放系数较难确定，严重限制了其在工程实践中的应用。文献[14]将速度误差作为模糊控制器的单输入来调整分数阶滑模控制器的阶次，但文中的模糊规则需要根据系统的仿真结果来制定，过程相对复杂，且并未进行相应的试验验证。文献[15]将滑模面及其导数的乘积作为模糊控制器的单输入变量来调整滑模控制器的参数，但其更注重系统的稳定性，很难有效提高系统的动态响应性能。

本文采用模糊滑模控制器来提高系统的动态响应性能并减小其抖振。滑模控制器采用等速趋近律，并用饱和函数代替符号函数，减小系统稳定时的抖振。将速度误差作为模糊控制器的单输入变量，根据制定的模糊规则实时调整切换增益的大小，实现电机转速的自适应控制。该方法简单、有效，在工程实践中具有较大的应用价值。

1 模糊滑模控制系统

PMSM的速度控制采用id=0的矢量控制系统，包括坐标变换、模糊滑模控制器、PI控制器，如图1所示。坐标变换包括Park变换和Clarke变换，通过数学运算得到三相电流在不同坐标系下的数值。速度误差经过模糊滑模控制器后得到其控制函数，即q轴电流iq。电流环采用PI控制器，并通过空间矢量脉宽调制(SVPWM)技术得到电机的驱动信号，从而驱动电机转动。

图1 模糊滑模控制系统

1.1 电机数学模型

在滑模控制中，需要得到PMSM的数学模型。由于PMSM强耦合、多变量等非线性因素的存在，建立精确的电机数学模型是很困难的。滑模控制具有强鲁棒性的特点，在实际应用中并不需要精确的电机数学模型。因此，在进行PMSM的建模时，假设三相绕组完全相等、气隙磁链呈正弦分布，并忽略磁路饱和、磁滞等现象，可得到电机的数学模型如下[16]：

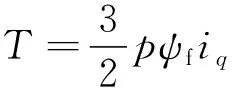
(1)

式中:T代表电机输出转矩;p代表电机的极对数;ψf代表永磁体磁链;iq代表q轴电流。

电机的动力学方程如下：

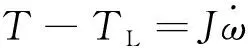
(2)

式中:TL代表负载转矩;J代表转动惯量;ω代表电机的角速度。

假设负载转矩为零，由方程式(1)和式(2)可得：

(3)

1.2 准滑动模态

滑模控制系统采用等速趋近律。为更好地消除滑模控制的抖振，控制系统采用准滑动模态，即在某一Δ邻域内(边界层)采用线性反馈控制，在边界层外采用切换控制。趋近律可表示为

(4)

在构建滑模面时，选取速度误差和其积分作为状态变量，可以有效减少因微分求导而引入的高频噪声。

系统的状态变量x1和x2为

(5)

式中：ωd代表速度指令。

滑模面s可表示为

s=x1+cx2

(6)

当系统到达滑模面后，速度误差将以指数方程的方式趋近于零，且趋近速度与系数c成反比。

由方程式(5)和式(6)可得：

(7)

由方程式(3),式(4),式(7)可得，控制函数iq可表示为

(8)

式中：d代表因参数变化、建模误差和干扰而导致的不确定性的界。在本文中，电机空载运行且未加任何外在干扰，因此，在不影响本文结论的前提下，为简化分析，将d设为0。

定义李雅普诺夫函数为

(9)

由式(9)可得：

(10)

1.3 模糊控制策略

在滑模控制器中，切换增益k的大小直接决定了控制系统的性能。若k设置的太大，系统会有严重的抖振而导致稳态误差太大；若k设置的太小，系统的动态响应速度太慢。

本文采用模糊控制，根据速度误差的大小来实时调整切换增益k。一般来说，模糊控制将速度和速度的导数作为双输入变量[8-13]。但是，速度导数会引入高频噪声，导致系统的缩放系数不好确定，同时，双输入变量会也会导致模糊规则相对复杂。为简化模糊控制系统的参数调试，进一步提高其在工程实践中的应用，本文将速度误差作为模糊控制的单输入变量，并制定了新的模糊规则。

速度误差e和切换增益k的论域定义在(-1,1)上。采用三角形隶属度函数将其分别定义为NB(负大)、NM(负中)、NS(负小)、ZE(零)、PS(正小)、PM(正中)、PB(正大)，如图2所示。隶属度定义在[0,1]范围内。以ZE为例，其隶属度函数可表示为

(11)

同理可得到NB、NM、NS、PS、PM、PB的隶属度函数。

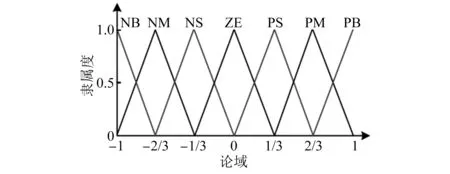
图2 隶属度函数

在计算隶属度时，将速度误差e除以速度指令值，确保e∈[-1,1]；然后，将e带入到NB、NM、NS、ZE、PS、PM、PB的隶属度函数，即可得到对应的隶属度。

模糊规则的制定原则为,当速度误差较大时，增大切换增益k以提高系统的响应速度；当速度误差较小时，减小切换增益k以减小系统的抖振。模糊规则如表1所示。

表1 模糊规则表

2 仿真分析

本文采用MATLAB中的Simulink模块对PMSM的模糊滑模控制器的调速系统进行了仿真分析，模糊滑模控制器的仿真框图如图3所示。PMSM使用科尔摩根公司的AKM21G型产品，母线电压为24 V。电机的转矩常数为0.1 N·m/A(rms)，线电阻和线电感分别为1.44 Ω和2.18 mH，极对数为3，转子的转动惯量为1.1×10-5kg·m2，电机的负载转矩为0，速度的参考指令值为225 r/min(对应试验中的标幺值0.03)。

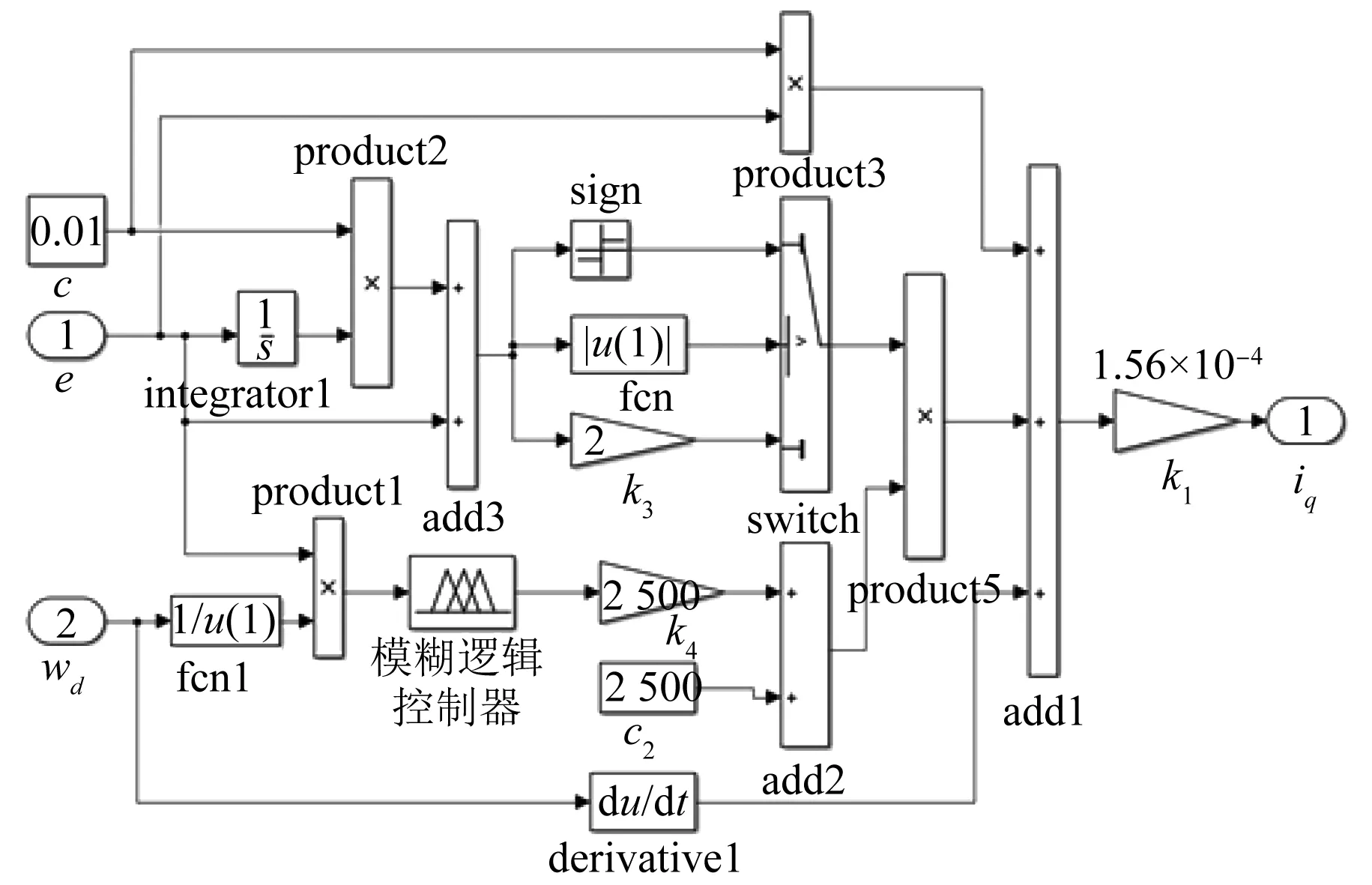
图3 模糊滑模控制系统仿真框图

图4 速度阶跃响应

当采用常规滑模控制器和模糊滑模控制器时，电机转速的阶跃响应分别如图4(a)和图4(b)所示，电流控制函数分别如图5(a)和图5(b)所示。与常规滑模控制器相比，采用模糊滑模控制器时系统的上升时间由0.013 9 s减小到0.011 5 s，速度稳定后电流控制函数稳定在0.2 A附近，其振动幅度由0.59 A减小到0.17 A。

图5 电流控制函数

综上所述，采用模糊滑模控制器可以有效提高系统的动态响应速度并减小系统的抖振。

3 试验验证

为验证模糊滑模控制系统的有效性，搭建了PMSM的嵌入式系统，如图6所示。控制芯片采用TI公司的DSP芯片TMS320F28335。在CCS6.1的开发环境下编写模糊滑模控制算法的程序，并通过仿真器控制硬件电路。在试验中，速度和电流的取值均为标幺值(速度的基准值为7 500 r/min，电流的基准值为2 A)。

图6 电机控制试验平台

图7 模糊滑模控制

采用模糊滑模控制器时，电机转速的阶跃响应和切换增益的变化分别如图7(a)和图7(b)所示。当转速误差较大时，切换增益变大，提高系统的响应速度；当转速误差较小时，切换增益变小，减小控制函数的抖振。采用常规滑模控制和模糊滑模控制的电流控制函数的抖振分别如图8(a)和图8(b)所示。与常规滑模控制器相比，采用模糊滑模控制器时系统电流控制函数的抖振由0.11(标幺值)减小到0.05，验证了模糊滑模控制器的有效性。

图8 电流控制函数

4 结 语

本文采用模糊滑模控制器来解决滑模控制系统抖振和动态响应性能之间的矛盾。模糊控制采用速度误差作为单输入变量，既简化了模糊规则，同时也减少了模糊控制系统所需要调试的参数个数，极大地方便了其在工程实践中的应用。滑模控制器采用饱和函数代替符号函数，进一步减小系统抖振。通过试验结果可知，采用模糊滑模控制器时，若转速误差较大，则切换增益变大，提高系统的响应速度；若转速误差较小，则切换增益变小，减小控制函数的抖振。