基于管理模型软件的不同场景下暴雨排水网络优化研究
阿依妮尕尔·艾尔肯
(新疆水利水电勘测设计研究院,乌鲁木齐 830000)
0 引 言
任何地区的发展都与适当提供最基本的公共服务有关,如能源、水和卫生设施[1]。在清洁服务中,必须适当处理废水和雨水,以减轻由于人与环境不断相互作用而造成的健康和公共风险问题[2]。雨水排水系统的目标是在降雨期间实现公共道路上雨水径流的快速疏散,从而避免对车辆和行人交通的影响,同时降低给定区域的洪水风险[3-4]。然而,尽管该设计考虑了天气、地质、岩土和地形条件,但在雨季期间观察到洪水地区和系统崩溃是很常见的。
针对上述问题,目前已有专家学者开发了建模和分析软件,这对污水系统的设计或检验阶段很有价值[4]。因此,为了满足国家标准的要求如卫生法规等,在非永久性流动条件下需要进行水力分析的情况下,为了确定整个系统的行为以及在污水网的不同部分和组成部分发生的故障,有必要构建水文模型,以获得设计上的水文曲线。本文研究使用暴雨水管理模型(SWMM)软件,这是一个免费的雨水管理模型,模拟降水从土壤表面通过渠道网络的运动。
此外,对城市污水系统的模拟和优化研究的目标是确定不同的水力参数,使此类项目的成本最低,从而保证污水系统不会发生溢出或超载。为此,本次研究开发了雨水污水管网的设计和优化,使用SWMM软件进行建模,并对其进行成本分析,以确定适用于特定研究区域的最合适替代方案,同时寻找可能发生洪水事件的解决方案。
1 研究方法
为了确定系统中的故障和组成系统的元素,下面介绍本研究中使用的方法和方程。
1.1 研究区域的定义
本次研究选取新疆的3个区域,它们具有不同的地形条件,但都满足面积等于或大于10 hm2的要求,实验研究在所选取的3个区域中随机获取,以保证结果的准确性,并得以获得相对可靠的结果。
通过使用Google Earth和CivilCAD等工具,在3个研究区内确定等高线,从而确定必要的高程,以确定街道中的水流,然后在不同的地形条件下进行设计。此外,每个街道的支流区域都是固定的,根据这些信息,可以发现流向每个研究区域的可能扩张,正如调查中所发生的那样,路面曲线是从流向洪水的地段进行的平面时间测量中获得的,代表重要信息,以便对道路和排水结构的表面流体动力学进行分析。
EPA SWMMH软件需要每个子流域的附加信息,如平均坡度和宽度。
1.2 用合理的方法设计雨水排水系统
为了设计暴雨排水网络,首先要根据国内暴雨排水网络设计相关要求提出的方法确定重现期,其中重现期是根据研究区域的排水特征得出的。因为同一区域内发生多个排水,其中一个支流面积在2~10 hm2之间,另一个支流面积大于10 hm2,因此决定采用10 a的回归期。因为在SWMM软件计划中,它必须管理一个单一的回归期。
为了确定收集器的位置,对街道上的水膜进行先前的分析,并将超过7 cm的水膜作为洪水标准。然后,根据水和基本卫生条例以及《Hidrología Aplicada》一书中的下列方程式进行计算,具体如下:
1.2.1 输入时间
本小节所示输入时间为径流到达收集器集水槽所需的时间,使用式(1)计算。需要注意的是,进入初始井的最短时间为5 min。
(1)
式中:Te为输入时间,min;C为分离系数,无量纲;L为地表径流的最大长度,m;S为最远点与网络入口点之间的平均斜率,m/m。
1.2.2 集中时间
本文中集中时间被理解为进入时间和在收集器中流动时间的总和。对于本例,因为没有收集器,它等于进入时间。初始井的最短浓缩(Tc)时间为10 min,最大浓缩时间为20 min。
1.2.3 强度设计
它是一个排水区域的平均降雨量,单位是mm/h。强度由设计降雨持续时间(D)和重现期选取,由式(2)表示。
(2)

1.2.4 设计流量
设计流量为根据合理方法定义的地表径流流量,适用于流域面积小于80hm2的情况,由式(3)定义。
Q=2.78*C*I*A
(3)
式中:Q为设计流量,L/s;C为径流系数,无量纲;I为设计降雨强度,mm/h;A为流域面积,hm2;2.78是换算系数。
此外,开发联络线功率是为了验证是否满足最小键深度条件,必须进行能量、键和托盘水平的计算,确保亚临界状态下不会产生回水。本节的制定考虑使用国内设计标准中的方程确定井中的下降。因为获得了较小的下降,不需要处理特殊的接头结构,与饮用水和基本卫生部门技术规范中关于EPM污水系统设计标准的公式进行了比较。
最后,在环境保护局的雨水管理模型软件中进行建模。作为第一步,考虑到SWMM软件用户手册,为构成模型的每个元素定义初始数据,以便于数据输入。随后,使用绘图工具,每个组成项目的元素都被详细阐述,直到获得最终模型。最后,对各研究区(高、中、低坡度)进行模拟。SWMM中的建模方法考虑了网络的拓扑结构,包括井、直径、截面长度、坡度、流量等元素。
2 结果分析
研究结果分为3个部分:暴雨排水网的优化、软件建模以及对初始设计和优化后的成本分析。
2.1 暴雨排水管网优化
根据每个模拟模型最后部分生成的水文图,对排水系统进行优化。首先,取峰值流量,并将其降低至一定百分比,以确保两者之间的时间不超过20 min。考虑到高边坡(图1)、中边坡(图2)和低边坡(图3)的超载时间分别为11、12和13 min,确定3个研究区30%的减量百分比,在所有情况下均满足所需时间。

图1 单位过程线流量-高边坡

图2 单位过程线流量-中边坡

图3 单位过程线流量-低边坡
2.2 建模与软件
定义不同场景中每个部分的减少百分比,并再次确定收集器的尺寸,其目的是减小直径,使系统在其最大容量下工作。随后,SWMM在逐渐变化的流量中再次对设计进行建模,以检查峰值流量的水位,给出与每个区域最具代表性的截面相对应的剖面图,见图4、图5和图6。正如在研究中所做的那样,它开发了对可能的水淹层高度的迭代,确定实现了洪水的等高线。

图4 水位在降水48 min时开始升高

图5 降水开始后48 min的水位-中坡度

图6 降水开始54 min后水位下降-低坡度
在图4中,P29井在最大产能下工作13.2 min,P38井在最大产能下工作19.2 min。图5显示,对于P2段渠道,P2井和P1井分别以最大容量工作7.2和7.8 min。图6显示,对于P6段通道1,P6井在最大容量下工作8.40 min。根据上述情况可以看出,水膜未达到井的最大高度,这反过来决定了管道以最大容量工作,这并不意味着周围街道存在洪水风险。
2.3 成本分析
在3个研究区域中,对传统设计和优化设计都进行了预算。表1、表2和表3显示了每个区域的成本差异。对于高坡度,优化节省96 876 058元,相当于17.8%;对于中等坡度区域,预算减少350 140 666元,相当于22.4%;而在低坡度区域,预算减少604 325 382元,相当于24.6%。通过分析获得的成本结果可以发现,优化设计最适合应用于3个确定的研究领域。
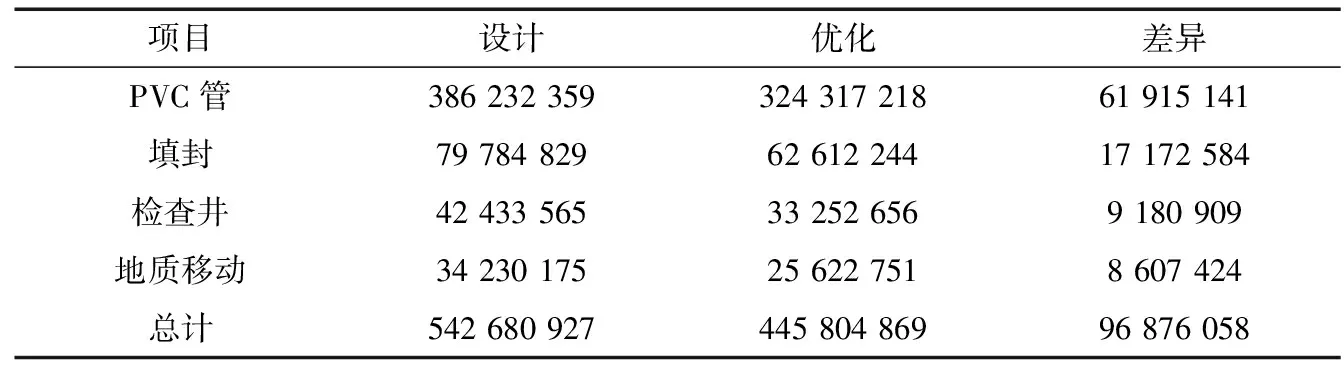
表1 成本变动-高边坡 /元
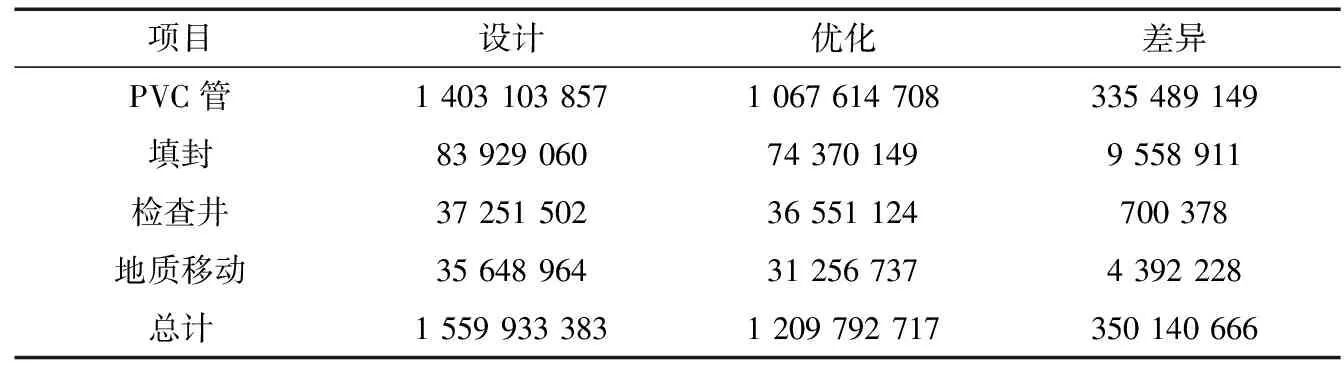
表2 成本变动-中边坡 /元

表3 成本变动-低边坡 /元
3 结 论
SWMM对每种设计进行建模,观察系统在非恒定流中的行为,即使设计符合国家标准规定的要求,但发现收集器部分满负荷工作,这意味着可以调整尺寸以提高其效率。
本文分析了设计所得的水文曲线后,估计污水系统一般水平的峰值流量减少30%。在分析软件中运行优化后的系统时发现,有些收集井达到了产能极限,但这并不意味着存在洪水风险。因为对这些井的持续时间进行分析后发现,初始设定的持续时间小于20 min。通过初始设计和优化设计,本文研究了不同条件下的成本结构,结果显示高边坡节约成本17.8%,中边坡节约22%,低边坡节约24.6%,主要体现在开挖和管径等选定上。

