基于正装迭代法的钢管砼拱桥吊杆初始索力计算

何炳涛

(佛山市公路桥梁工程监测站有限公司， 广东 佛山 528041)

系杆拱桥主要由拱肋、纵梁、吊杆和桥面系组成，结构外部静定、内部超静定，受力复杂，施工中主要通过分阶段多次调整索力使其达到理想受力状态，如何控制和调整吊杆初始张拉索力成为施工控制成功与否的关键。计算吊杆初始张拉索力的方法主要有无应力状态法、正装迭代法、倒装法等。该文结合工程实例，采用正装迭代法计算钢管砼拱桥吊杆初始索力。

1 正装迭代法的基本原理

正装迭代法先假定一个吊杆索力，根据这个吊杆索力通过正装计算得到相应理想成桥状态下吊杆索力，再对2组数据进行比较，计算差值；根据差值假定新的初始吊杆索力，再次进行正装计算。如此循环，直到2组数据差值最小为止。桥梁施工中，采用正装迭代法能很好地考虑成桥过程中结构单元非线性因素及砼的收缩徐变。计算过程如下：

(1) 假定某个吊杆索力为a。

(2) 输入成桥索力b，进行第i次正装迭代，得到计算索力c。

(3) 通过相应的影响矩阵进行有限元分析，令b=a，求得吊杆索力c。

2 工程实例计算与分析

2.1 工程概况

广东佛山桂江大桥主桥为下承式预应力砼吊杆钢管拱桥，主跨跨径为63 m、56 m，主拱拱肋采用直径为110 cm的圆形钢管砼结构。主跨跨径为56 m的拱肋主线为y=-1/121.976(x-27.5)2+12.4的二次抛物线，相应计算跨径为55 m，计算矢高为12.4 m，矢跨比为1/4.44；主跨为63 m的拱肋主线为y=-1/155(x-31)2+12.4的二次抛物线，相应计算跨径为62 m，计算矢高为12.4 m，矢跨比为1/5。主跨纵向每榀拱肋共设11根吊杆，主跨63 m吊杆间距为5 m，主跨56 m吊杆间距为4.3 m。吊杆与拱肋端部结合为整体现浇，主梁采用整体现浇，吊杆轴线和桥面按道路竖曲线实施。设计荷载等级为公路-Ⅰ级。主桥布置见图1。

图1 主桥桥跨布置示意图

2.2 主桥有限元模型

采用MIDAS/Civil建立该桥有限元模型(见图2、图3)，主梁和拱肋采用梁单元模拟，吊杆使用桁架单元模拟，吊杆和拱肋采用刚性连接。一期恒载有主梁、横隔板及拱肋等自重，主梁自重按实际断面计算，容重为26 kN/m3；横隔板使用集中荷载模拟。二期恒载有桥面铺装、灯柱、泄水管、调平层及防撞栏杆等，按70 kN/m计算。活载为公路-Ⅰ级。

图2 56 m跨MIDAS/Civil计算模型

图3 63 m跨MIDAS/Civil计算模型

2.3 正装迭代法计算分析

采用正装迭代法计算该桥在合理成桥状态下每个施工过程的受力情况，分析该桥施工过程中结构内力和变形。该桥每榀拱肋共设置11根吊杆，吊杆采用PES(FD)7-61低松弛镀锌平行钢丝索。主梁采用满堂支架施工，主梁及拱肋浇筑完成后进行第一次吊杆张拉，张拉至初始张拉力。

调整每个阶段的张拉索力为每根吊杆的第二次张拉吊杆索力，以最终确定的合理成桥下吊杆索力为最终目标参数，进行正装迭代，每榀的张拉吊杆数量为22根。控制参数为合理成桥状态下控制截面的弯矩和成桥吊杆索力，控制参数数量m为控制截面和吊杆数量，m=27个。每次正装迭代后将计算结果和合理成桥下结果进行对比，根据两者差值进行调整并再次进行迭代。控制截面见图4，最后一次迭代所得控制截面弯矩、吊杆索力与合理成桥阶段结果的对比见图5～7。

图4 控制截面示意图

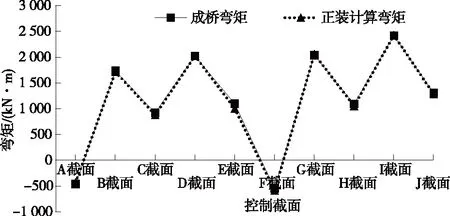
图5 控制截面弯矩对比

从图5～7可以看出：正装迭代计算所得控制截面弯矩、吊杆索力与成桥状态下弯矩、吊杆索力基本吻合；弯矩最大差值出现在E截面，相差8.9%；吊杆索力最大差值出现在右侧R13-8#吊杆，相差4.3%。

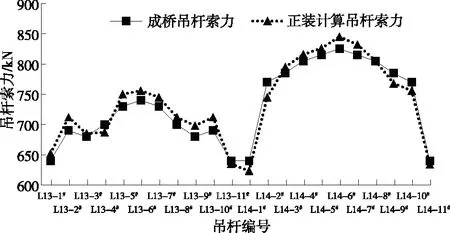
图6 左侧吊杆索力对比

图7 右侧吊杆索力对比

3 结论

结合佛山桂江大桥，采用正装迭代法计算钢管砼拱桥吊杆初始索力，得到以下结论：

(1) 采用正装迭代法计算所得控制截面的弯矩、吊杆索力与成桥状态下弯矩、吊杆索力基本吻合，且计算较简单、快捷。

(2) 正装迭代计算所得控制截面的弯矩、吊杆索力与成桥状态下弯矩、吊杆索力的最大差值分别出现在E截面(相差8.9%)和右侧R13-8#吊杆(相差4.3%)。采用正装迭代法计算吊杆索力存在一定误差，建议进行多次迭代，提高计算精度。