日照下波形钢腹板箱梁桥竖向温度分布研究*

刘阳帆， 钟扬， 樊林杰， 袁以鑫

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114；2.湖南机场管理集团有限公司， 湖南 长沙 410141)

桥梁处于露天的外界环境中，受太阳辐射等环境因素的影响，桥梁结构会产生较大温度应力。目前对砼桥梁温度效应或温度场的研究较多，但对波形钢腹板箱梁桥温度效应或温度场的研究还不完善。赵品等根据波形钢腹板箱梁桥观测数据，提出了波形钢腹板箱梁温差计算模式。姚晨等通过对波形钢腹板箱梁桥的长期观测，提出了顶板横向正应力温度计算公式。陈中刚等对波形钢腹板箱梁桥横向温度应力进行计算，并与砼箱梁桥进行比较，得出波形钢腹板箱梁桥由温度变化引起的内力变化较小。董旭等对大跨度波形钢腹板箱梁桥进行现场实测，分析其温度效应，提出了温度梯度模式。大部分研究针对某地区的波形钢腹板箱梁桥，温度梯度模式根据测量数据通过拟合确定。该文基于桥梁日照温度场分布，结合适用于波形钢腹板箱梁桥的温度场求解方法，参考国内外箱梁桥温度作用研究现状，研究波形钢腹板箱梁桥竖向温度梯度模式。

1 温度场分布特性和求解方法

1.1 温度场分布特性

在日照、大气温度、风速等作用下，桥梁内部温度场发生变化。桥梁结构内部热量传递主要取决于材料的导热系数，钢材的导热性好，砼的导热性能比钢材差很多。波形钢腹板箱梁的底板受到的日照时间最短，且处于高空，通风冷却效果很好，是整个箱梁截面温度最低的位置。地面、水面或大气将太阳辐射反射到箱梁底板底面，导致底板竖向存在一定温差。

1.2 温度场的求解方法

实际工程中大都使用指数函数描述截面的竖向温差。文献[8]根据实测数据建立的沿梁高方向的温差分布函数为：

Ty=T0e-ay

(1)

式中：T0为沿梁高方向的温差；y为计算点至顶板表面的距离(m)；a为指数，受结构形式等因素的影响。

2 竖向温度梯度模式

由于波形钢腹板箱梁桥的材料特性不同及腹板形式的变化，规范中温度梯度模式不一定适用。下面通过对波形钢腹板箱梁桥顶板、波形钢腹板及底板温度的分析，研究其竖向温度梯度分布。

2.1 顶板

波形钢腹板箱梁桥顶板为砼结构，温度分布形式与砼梁桥相差无几。主要受太阳辐射的作用，顶板表面温度较高，远离顶板的位置温度迅速降低，顶板的竖向温度可采用式(1)来表达。

2.1.1 顶板竖向温差

无本地区实测数据时，可根据所在地区气象及经纬度等构建理想的经验公式。文献[11]采用逐步回归法，根据当地气象数据得到箱梁顶部温差预测公式[见式(2)]，该公式能较准确地预测不同地区桥梁结构的竖向温差。因此，波形钢腹板箱梁桥顶板竖向温差采用式(2)计算。

T0=2.57+0.181ΔT+(0.534I-0.002 691I2)-

(1.32v-0.208v2)

(2)

式中：T0为顶部温差；ΔT为日大气温差；I为日最大太阳辐射量(MJ/m2)；v为风速。

太阳辐射强度采用Hottel模型计算，根据辛普生法通过积分得到全天水平地面上的太阳辐射能量。

2.1.2 指数a的取值

大多根据实测数据确定指数a的取值。若无实测数据，可通过砼梗腋高度yg来确定。如图1所示，yg为：

图1 梗腋示意图

yg=(m+n)/2

(3)

式中：m为箱内梗腋转折点到顶板顶面的距离；n为箱外梗腋转折点到顶板顶面的距离。

桥面铺装厚度为0、50 mm、100 mm时，a可分别通过-3.20yg+5.66、-2.39yg+4.88、-2.15yg+4.30计算得到。

2.2 波形钢腹板

温度影响需考虑不同材料间的热传递及钢板受热性能与砼板的不同。波形钢腹板的导热性能是砼板的几十倍，其温度变化幅度较小。考虑到波形钢腹板与砼板交界处有热交换发生，其上下翼缘处的温度较低。

在日照作用下，上翼缘存在一定阴影面，不会受到太阳直接辐射。阴影长度通过悬臂长度计算得到，公式如下：

B=Asinh/sin(β-h)

(4)

式中：B为阴影长度；A为翼缘板长度；h为太阳高度角；β为腹板与水平面的夹角。

为便于计算，将波形钢腹板简化为非稳态无内热源的温度场。因为波形钢腹板的厚度较小，且导热性能良好，近似认为其仅有竖向温差，横向温度梯度分量为零。热交换过程由傅立叶定律转换得到：

qc+qr+qs=-k∂T/∂yny

(5)

式中：qc为对流换热热流密度(W/m2)，按式(6)计算；qr为热辐射换热热流密度(W/m2)；qs为太阳辐射换热热流密度(W/m2)；k为导热系数；∂T/∂y为温度梯度在坐标系上的分量；ny为法线的方向余弦。

qc=hc(Ta-Ts)

(6)

式中：hc为对流热交换系数(W/m2·℃)；Ta为空气的绝对温度；Ts为表面的绝对温度。

hc的计算公式为：

hc=6.31v0.656+3.25e-1.91v

(7)

在没有大气温度实测数据时，可参考余弦函数，按下式计算空气的绝对温度：

Ta=θv+θscos[π(t/3 600-t0)/12]

(8)

式中：θv为日平均气温；θs为日温度变化幅值；t为当日某时刻；t0为当日气温最大的时刻。

长波热辐射导致的换热热流密度qr可通过斯特藩-玻尔兹曼定律表示为：

(9)

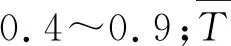
考虑太阳辐射导致的热交换，太阳辐射换热热流密度qs可表示为：

qs=atIt

(10)

It=Ia+Iβ+If

(11)

式中：at为太阳辐射吸收系数；Ia为太阳直接辐射；Iβ为散射辐射；If为反射辐射。

散射辐射从天空的各个方向辐射到地球表面，可表示为：

Iβ=0.5J0sinhsin2(β/2)(qa-qT)

(12)

式中：J0为太阳常数，J0=1 367 W/m2；β为腹板与水平面的夹角；qa为扣除大气吸收的透射系数；qT为大气总透射系数。

因为桥梁结构一般离地表较近，波形钢腹板箱梁桥会受到反射辐射。反射辐射计算公式为：

If=0.5J0Rsinhcos2(β/2)(qa-qT)

(13)

式中：R为反射系数。

将砼顶、底板表面温度作为波形钢腹板的边界条件，结合上述公式，根据热流平衡，桥梁表面热流密度在一段时间后处于相对平衡状态，解平衡方程即可得到任意时刻波形钢腹板表面温度。通过计算各点热流密度并运用傅立叶定律得到各点温度，从而得到波形钢腹板的竖向温度变化。

2.3 底板

底板主要受到反射辐射的影响，直接辐射和散射辐射的影响较小，且底板温度远低于砼顶板。在考虑日照作用形成的正温度梯度时，普遍认为桥梁底部存在一定温差，但温差变化较小，根据美国规范AASHTO，最大温差在3 ℃以内，故考虑用线性表示。

底板温度梯度斜率可根据底板下缘温度减去底板上缘温度除以底板高度求得。查阅相关文献及美国、新西兰规范，底板上缘温度梯度接近于零。参考新西兰桥梁规范，波形钢腹板箱梁桥底板上下缘的温差取1.5 ℃。

综上，顶板温度分布模式采用指数函数，波形钢腹板与底板的温度分布模式采用线性函数(见图2)，计算公式如下：

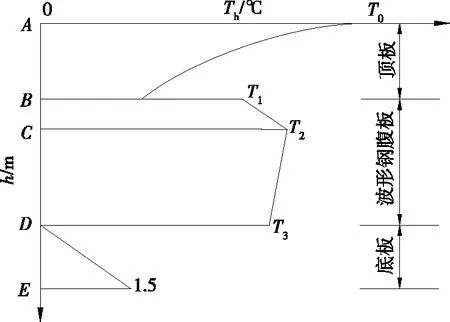
图2 竖向温度梯度模式

(14)

式中：Ty为沿波形钢腹板高度y的竖向温度；T0为顶板上下缘最大温差值；T1、T3分别为波形钢腹板顶面、底面温度；T2为波形钢腹板上的最高温度。

3 实测温度场对比分析

3.1 工程背景

前山河特大桥主桥跨径布置为90 m+160 m+90 m，波形钢腹板箱梁桥顶、底板采用C50砼，顶板宽度为15.75 m，设2%横坡。采用1600型波形钢腹板，板厚22 mm。跨中截面尺寸见图3，材料参数见表1。

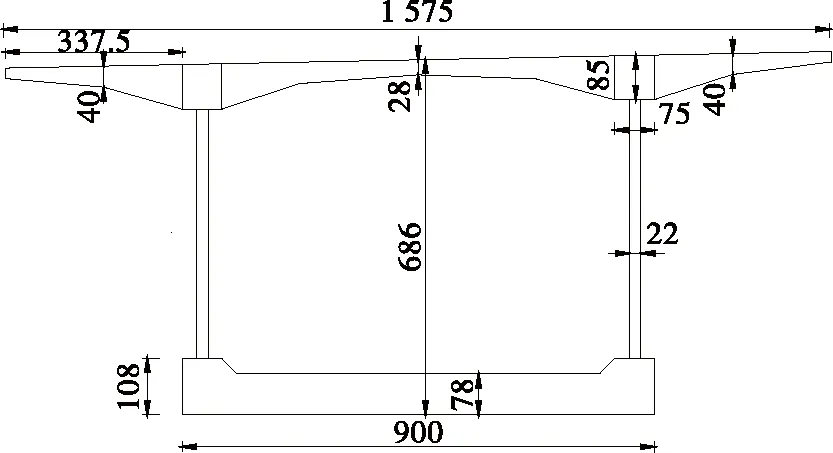
图3 跨中截面尺寸示意图(单位：cm)

表1 材料参数

3.2 有限元建模

采用ANSYS软件建立箱梁有限元精细化模型(见图4)。砼顶板、底板选用实体单元Solid45模拟，波形钢腹板选用壳单元Shell93模拟。壳单元和实体单元连接处采用共节点，主节点为壳单元的节点，考虑自由度设置约束方程形成刚性连接。

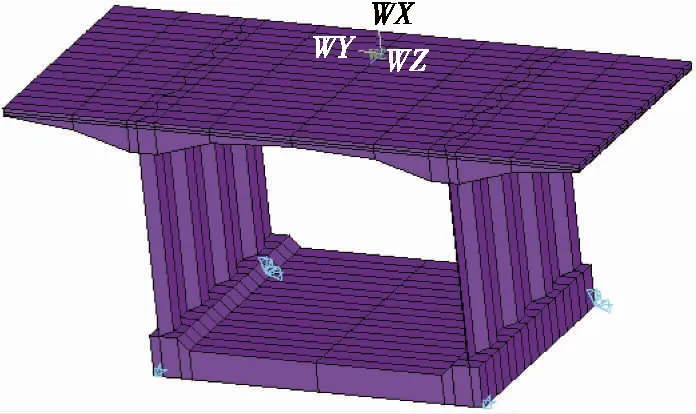
图4 箱梁空间有限元模型

在7月23日16：00时对该桥进行温度场测量。依据气象资料，当日大气温差为7.1 ℃，风速为3 m/s。根据太阳直射、散射和地面反射等因素，顶板的温度梯度为19.84e-2.94y，计算得到顶板底面温度为1.63 ℃。底板顶面温度取零。将两者作为波形钢腹板顶面和底面温度的初始边界条件，计算得其温度梯度为：

(15)

采用ANSYS进行分析，设荷载步时间为3 600 s。根据阴影状态判断腹板上是否有太阳直接辐射作用。长波热辐射、太阳辐射和对流采用综合气温、综合热对流系数施加在边界节点上。该桥16：00时温度计算结果见图5，与计算所得竖向温度差值基本一致。

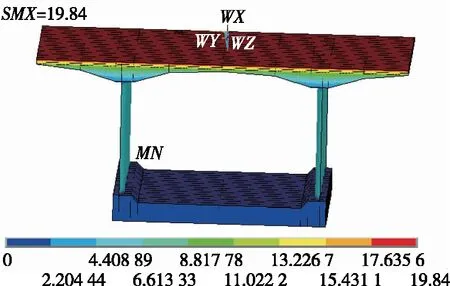
图5 箱梁16：00时温度云图(单位：℃)

3.3 对比分析

将实测温度与按JTG D60—2015《公路桥涵通用设计规范》温度梯度计算所得竖向温度、采用文中温度梯度计算所得竖向温度进行对比，结果见图6。

图6 实测温度与计算温度对比

由图6可知：采用文中温度梯度模式计算得到的温度与实测数据非常接近，与规范计算值相比，顶板数值与变化十分相近。虽然《公路桥涵通用设计规范》中温度梯度计算值在顶板上缘与实测温度相差不大，但在波形钢腹板及底板处没有温度变化。而根据实测数据，波形钢腹板与底板处存在一定温度变化，在选取规范中温度梯度模式时应注意这一点。

实际工程中，箱梁顶、底板处易出现裂缝，尤其是顶、底板中轴线上纵向裂缝较多，影响桥梁结构的正常使用。将文中温度梯度模式与《公路桥涵通用设计规范》中温度梯度模式进行横向温度应力对比，结果见表2。

由表2可知：2种温度梯度模式下横向温度应力作用方向基本一致，且除顶板中轴线下缘横向拉应力外，采用《公路桥涵设计通用规范》温度梯度模式得到的横向温度应力都比文中温度梯度模式的大。在无实测温度的情况下，采取规范中温度梯度模式进行设计时，应考虑顶板下缘横向温度拉应力。

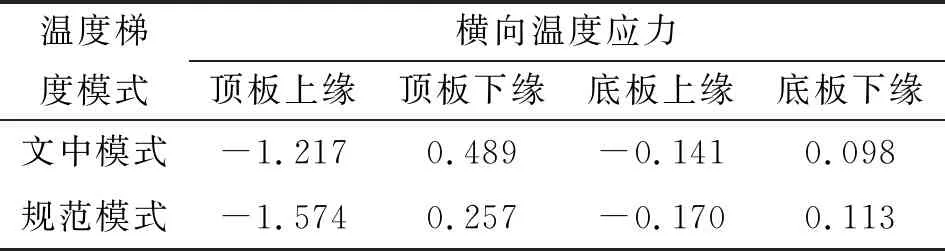
表2 不同温度梯度模式下横向温度应力 MPa

4 结论

(1) 提出一种在无实测数据的情况下考虑太阳辐射、大气温度、风速等参数的温度梯度模式，算例表明，利用该模式能较精确地计算不同地区的竖向温差，为温度荷载效应计算提供参考。

(2) 波形钢腹板箱梁桥设计时，在无实测温度数据而选用《公路桥涵通用设计规范》中温度梯度模式的情况下，应重视顶板中轴线下缘横向温度拉应力。