基于深度神经网络的海表盐度反演

高明，黄贤源，王芳，张海龙，赵红霞，高溪远

（1.中国人民武装警察部队作战勤务保障大队,北京 100081；2.中国人民解放军部队92859 部队,天津 300000）

海表盐度（Sea Surface Salinity，SSS）是研究海洋状态和海水动力循环的重要物理和化学参数。海洋中海-气交换、海冰冻融等许多过程的产生和发展都与盐度的分布及变化规律有关，研究海表盐度对揭示海洋现象、海洋过程和全球气候变化具有重要意义[1-2]。

海表盐度探测手段主要包括实地探测和遥感探测。实地探测手段难以实现全球海域的实时连续观测，但海洋卫星遥感技术可较好地解决这一问题。欧洲航天局（European Space Agency，ESA，简称欧空局）于2009 年发射的土壤湿度与海水盐度（Soil Moisture and Ocean Salinity，SMOS）卫星是一颗专用于探测海表盐度的卫星，其唯一有效载荷是基于孔径综合技术的微波成像仪MIRAS（Microwave Imaging Radiometer using Aperture Synthesis），工作频率在L 波段，主要用于探测辐射亮温（Brightness Temperature，TB）。在发射之初，该卫星提出的观测目标是提供在空间分辨率为200 km × 200 km、时间分辨率为10～30 d 时精度达到0.1 的全球海表盐度数据。但是，研究表明[3-4]，在某些海域，SMOS 卫星的盐度产品难以达到预期要求。对此，许多学者开展了提高SMOS 卫星盐度数据精度的研究[5-8]。例如：卢红丽等[5]研究了海面风矢量对海表亮温的影响，并推导出海表风速、风向、海表亮温以及亮温修正量之间的关系式，从而消除了风对盐度遥感的影响。李志等[6]对风速和涌浪两个参数做线性回归，建立了适用于实验海区的盐度反演模式。邓广等[7]采用统计学的回归方式，将亮温数据代入HYCOM 模式的模拟亮温，建立回归模型，提高了南海区域的盐度反演精度。王迎强等[8]利用MPM 93（Millimeter-Wave Propagation Model 93）模型和最大似然估计法研究不同天气对盐度反演的影响，结果表明降雨量和海表面温度对盐度反演的影响不可忽略。

近年来，深度神经网络（Deep Neural Network,DNN）在智能驾驶、语音识别、医疗和生物等领域得到了广泛的应用[9-10]，也逐渐在海洋科学领域得到运用[11-13]。为提高SMOS 卫星盐度产品精度，本研究提出了基于深度神经网络的盐度反演算法，通过学习深层次非线性的网络结构，实现复杂函数的逼近，能够有效解决传统海表盐度反演模型中参数拟合复杂、模型适应性差等问题。K 折交叉验证法是机器学习（Machine Learning,ML）数据处理常用的方法，它能够充分利用有限的数据集，使其发挥最大效果，多用于训练数据量较少的情况，本文利用该方法进行12 次不同参数的实验，逐步调整深度神经网络的隐藏层数、层间结点数量、迭代次数、优化器种类以及Dropout 比例，进而不断优化模型结构，最终训练出最佳模型，以期为SMOS 盐度精度的提高贡献新的研究思路。

1 数据来源

1.1 研究区域

受射频干扰RFI（Radio Frequency Interference）的影响，微波辐射计接收的辐射信号存在不可消除的误差，大大降低了海表盐度的产品精度[14]。因此，本实验选择远离陆地，受RFI 影响较小的开阔海域作为研究对象。此外，银河噪声在7 月和8 月波动比较小，使用此时间段的SMOS 卫星数据可忽略来自外太空的影响[8]。基于此，本文选取太平洋中部海域（150°E～180°，5°～30°N）作为研究区域（图1 中红色方框区域），对该区域内2013 年7 月至8 月的数据进行时空匹配，构建实验所需要的数据集。

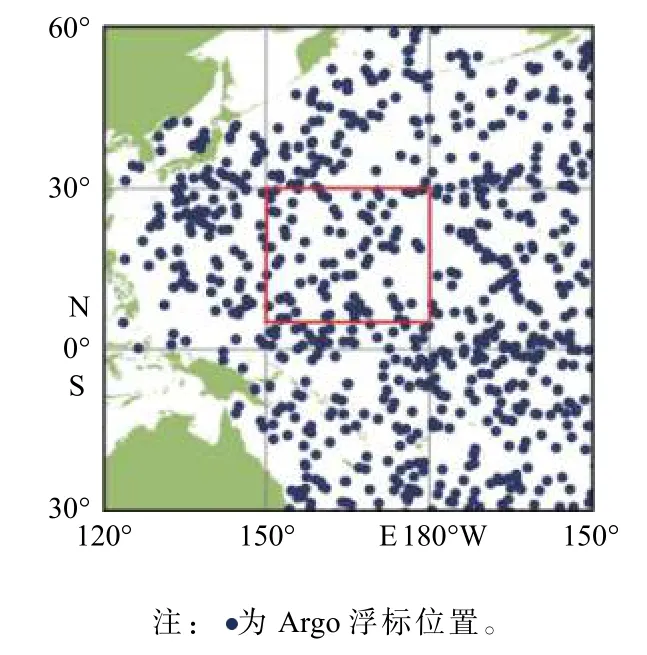
图1 研究 区域Fig.1 Study area

1.2 SMOS 数据

SMOS 探测的亮温不是海面的真实温度，而是一种用于描述物体辐射强度的假定温度。对于海洋表面，海水亮温与真实海表温度、海表发射率之间的函数关系[6]为：

式中：SST（Sea Surface Temperature）为海表温度；f为微波频率；Tb为亮温；θ为入射角；e为海表发射率；SSS 为海表盐度。

海表发射率e与海面粗糙度联系紧密。海面粗糙度主要由海面风速包括纬向风速（Zonal Wind Speed，ZWS）和经向风速（Meridional Wind Speed，MWS），以及有效波高（Significant Wave Height，SWH）表征[6]。此外，研究表明[15]，降雨率（Rain Rate，RR）和海表蒸发量（Evaporation，Eva）也是直接影响海表面实时盐度的重要因子。因此，本文选取与盐度反演密切相关的7 个参数，即：亮温TB、海表温度SST、纬向风速ZWS、经向风速MWS、有效波高SWH、降雨率RR 和海表蒸发量Eva 作为模型输入参数。这些参数和3 种SMOS卫星L2 级盐度产品（SSS1、SSS2、SSS3）均源于欧空局网站[16]，空间分辨率为0.022°×0.022°。

1.3 Argo 数据

Argo 浮标（以下简称Argo）是海洋实地探测的一个典型代表。它是一种自持式剖面漂流浮标，可以在大洋中自主沉浮、自由漂流，自动测量深至水下2 000 m 的海水剖面数据。Argo 所载的泵抽式温盐深仪（Conductivity Temperature Depth，CTD） 在距海表5 m 左右时会自动停止工作，无法探测到真实的海表盐度。但5 m 处的盐度与海水表层1 cm 左右的盐度值几乎一致[17]，因此，本文使用Argo 最浅层的盐度数据来代表海表盐度值。研究数据来自中国Argo 资料中心[18]，选择2013 年7 月至8 月太平洋中部海域（150°E～180°，5°～30°N）的Argo 浮标，具体位置见图1 中蓝点所示位置。

2 研究方法

2.1 数据匹配

SMOS 卫星提供的是200 km×200 km 的网格亮温数据，Argo 提供的是离散点数据，二者数据格式存在差异。因此，在建立神经网络模型之前，首先需要对SMOS 卫星数据与Argo 实测盐度数据进行时空匹配。

参考曹凯翔等[19]的数据匹配方法，本文采用空间分辨率为0.5°×0.5°、时间分辨率为36 h 的匹配原则，对2013 年7 月至8 月的SMOS 卫星L1、L2 级产品与Argo 盐度数据进行时空匹配，即：对于每一个SMOS卫星产品数据，计算其测量点周围0.5°网格点内和测量时间点（±18）h 内所有Argo 盐度的平均值，将其作为匹配后的实测盐度数据。

将SMOS 卫星数据与Argo 盐度数据匹配后，得到470 组有效数据。每组数据具有11 个属性值，即TB、SST、RR、SWH、ZWS、MWS、Eva，以及Argo 实测盐度数据、SSS1 数据、SSS2 数据和SSS3 数据。其中，将TB、SST、RR、SWH、ZMS、MWS 和Eva 这7 个参数作为反演模型的输入值，将Argo 实测盐度数据作为真实参考值，将SMOS 卫星的3 种L2 级盐度产品SSS1、SSS2、SSS3 数据作为与实验结果的比较值。

由于反演模型输入所需的7 个属性值的单位不同，所以，需要消除量纲之间的差异。利用标准归一化的方法，对每个参数减去其平均值（中心化），再除以其标准差，最终得到平均值为0、标准差为1 的标准正态分布数据。标准归一化后的参数x∗为：

式中：x为原始输入参数值；µ为参数的均值；σ为参数的标准差。

2.2 K 折交叉验证法

K 折交叉验证法是机器学习模型调优常用的方法，可以充分利用有限数据，发挥小样本的最大效果[20]。该方法的操作流程为：首先将数据集划分成数量相同的K 组数据，实例化K 个相同的模型，让每个模型都在K−1 个分区上训练；然后在剩余的一个验证分区上进行评估，模型的最终验证结果为k 个结果的平均值。本文采用4 折交叉验证，即K=4，如图2 所示。

图2 四折交叉验证法操作流程Fig.2 Four fold cross-validation process

2.3 DNN 深度神经网络

深度神经网络DNN（Deep Neural Network）是具有多个层级结构的人工神经网络，包括输入层、多个隐藏层和输出层。模型相邻层的节点间存在连接结构，而同一层和跨层的节点间没有连接。不同节点间通过全连接层与激活函数组合的形式相连，构建多层复杂的神经网络模型。模型结构如图3 所示。

图3 DNN 模型 结构Fig.3 DNN model structure

DNN 神经网络的构建包含了全连接层、激活函数、损失函数和优化器等结构。DNN 利用前向与反向传播算法（Backward Propagation，BP）进行训练，对网络中每个权重w和偏置b进行不断更新。反向传播算法作为DNN 的核心内容，实质是将预测输出值与真值间的误差进行回传，不断修改网络模型每个连接层中w与b的数值大小，使误差值不断减小，直至满足精度要求。通过大量数据的训练，损失函数值下降到要求阈值后，取此时的参数值作为模型参数，据此进行回归预测。针对不同的实际情况，隐藏层数、隐藏层节点数、Dropout 比例等结构参数与初始学习率、训练步长等训练参数的选取均会对训练结果产生一定的影响。此外，选取合适的损失函数与优化器，还可以提升网络模型精度，加速网络训练速度。BP 算法的权重与偏置计算公式为：

式中：w*和w分别为更新后和更新前的权重；b*和b分别为更新后和更新前的偏置；α为人为设置的学习率；J(w,b)为模型的损失函数。通过不断的梯度下降迭代，得到最优参数w*和b*。

3 实验流程

实验具体流程如图4 所示。首先将匹配成功的470 组数据进行标准归一化预处理，以统一输入变量量纲，然后按照7∶3 比例随机分为训练集330 组和测试集140 组。为使DNN 模型发挥最佳效果，本文进行了12 次不同参数设置的实验，对于每一参数设置，均进行了多次重复实验。表1 给出了12 次实验调参训练结果，数据为同一参数设置下多次实验的平均值。实验采用4 折验证法，将用于训练的330 个数据分为4 组，第一组和第二组均包含82 个数据，第三组和第四组均包含83 个数据。首先以第一组为验证数据集，在后3 组数据上训练模型，训练完成后，在第一组数据上验证盐度反演精度；接着以第二组数据为验证数据集。依次类推，不断修改隐藏层层数Hidden_Layer、隐藏层节点数Nodes、Dropout 比例Dropout_P 和具体优化算法Optimizer 等参数，最终得到最优模型。

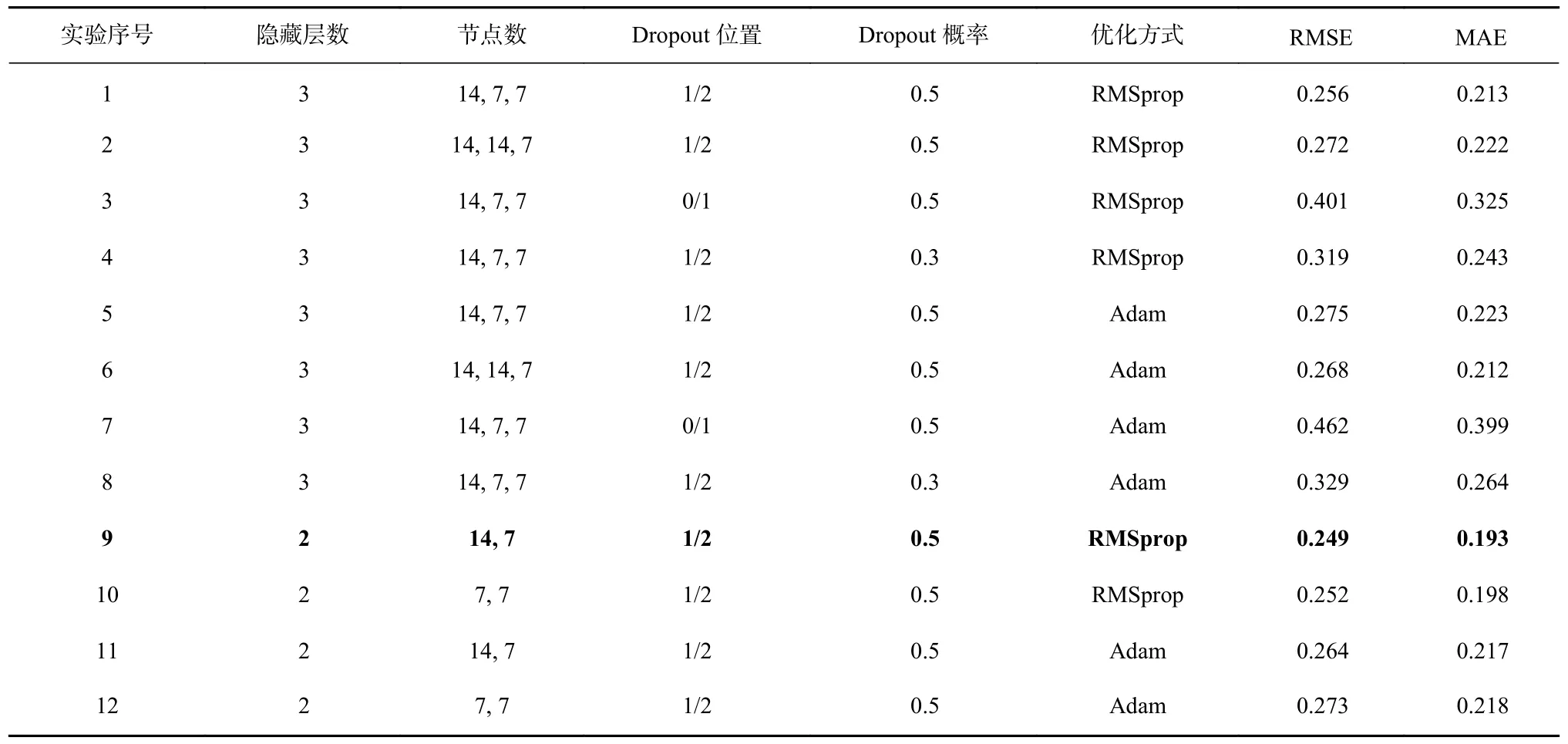
表1 12 次实验调参训练结果Table 1 Training results of 12 experiments

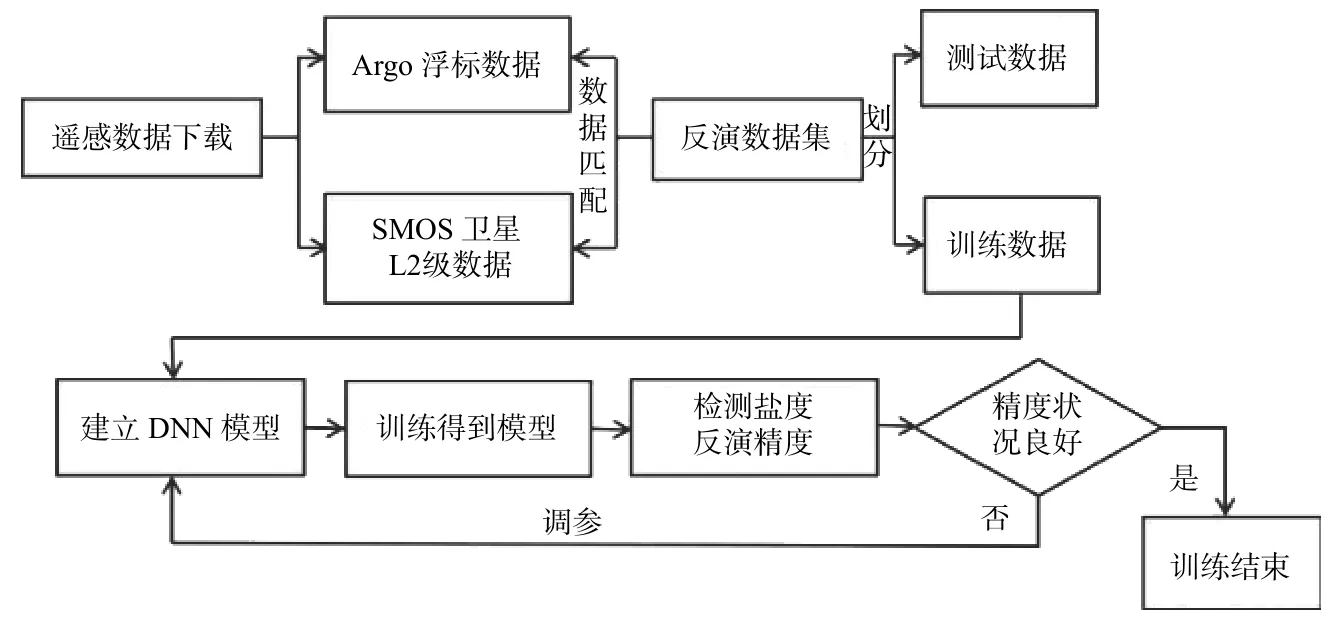
图4 基于DNN 深度学习算法的海表盐度反演流程Fig.4 SSS inversion flow based on DNN deep learning algorithm

本实验利用均方根误差（Root Mean Square Error,RMSE）和平均绝对误差（Mean Absolute Error,MAE）两个指标量化分析反演盐度的误差，计算公式分别为：

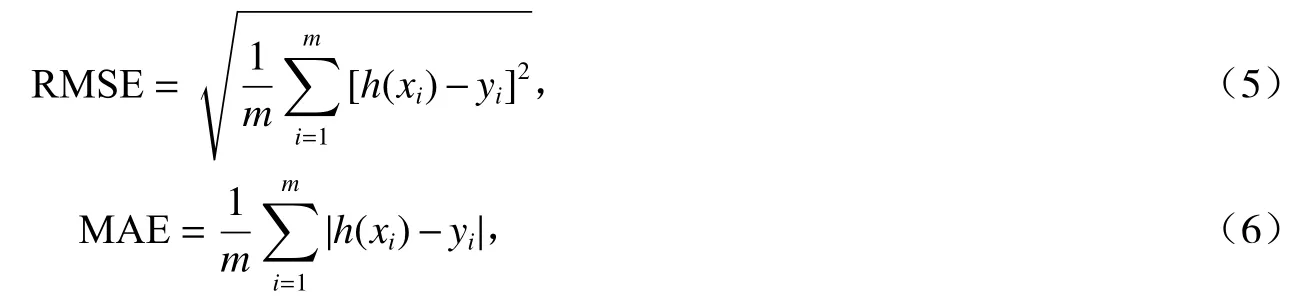
式中：m为实验数据总数；h(xi)为本文算法得到的海表盐度数据；yi为对应的实测Argo 盐度数据。

本文进行的12 次实验参数设置如表1 所示。由表1 可以看出，总的来说，当隐藏层为2 层时，模型反演得到的盐度误差低于3 层隐藏层模型反演的盐度。最优的反演盐度数据出现在第9 组，此时隐藏层为2 层，各层节点数分别为14 和7，Dropout 比例为0.5。采用RMSprop 优化方式，获得了RMSE 和MAE 分别为0.249 和0.193 的海表盐度。实验9 最优模型的其他重要参数学习率Learning_rate、激活函数Activation_function、损失函数Loss_function 和迭代次数Iteration 等的设置如表2 所示。

表2 最优模型的各参数及其数值Table 2 Parameters and values of the optimal model

4 结果与分析

本文实验9 的参数设置获得了精度最高的海表盐度数据。在该实验的模型训练过程中，训练集和测试集的平均绝对误差MAE 下降情况如图5 所示。在实验的前100 次迭代内，MAE 快速下降，模型迅速更新权重和偏置，使输出盐度与Argo 实测盐度尽可能相等。但在进行约120 次迭代后，MAE下降速度急缓，直至几乎不再下降，此时精度约为0.2。

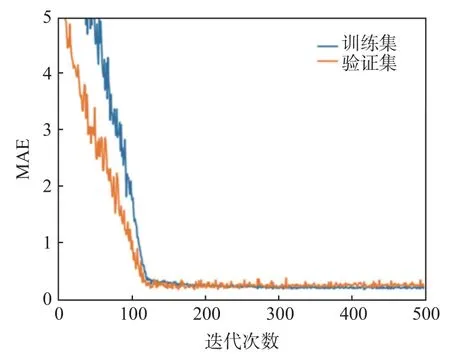
图5 训练过程中训练集和测试集的 MAE 变化Fig.5 MAE variation and test-sets during training

以Argo 实测盐度数据作为真实参考值，对实验获取的470 组盐度数据分别与SMOS 卫星的SSS1、SSS2、SSS3 三种盐度产品的RMSE 和MAE 进行比较（见表3），可以看出，SMOS 卫星的3 种盐度产品精度整体相当，但SSS1 的精度略高，因此选择SSS1 数据作为SMOS 卫星盐度产品的代表，与本文实验结果进行比较。

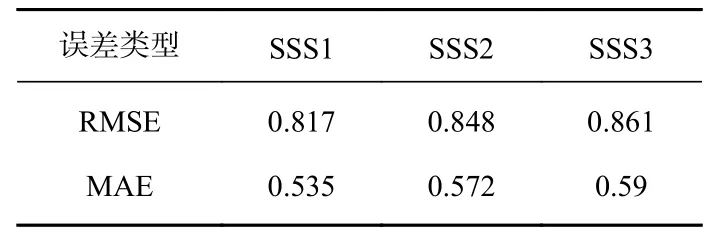
表3 SMOS 海表盐度产品SSS1、SSS2、SSS3相较于Argo 实测盐度的误差对比Table 3 Errors of SMOS sea surface salinity products SSS1,SSS2,SSS3 compared with Argo SSS

将140 组测试集数据代入训练完成的DNN 模型，得到测试集的反演盐度值。由DNN 反演盐度数据、SMOS 卫星产品SSS1 数据和Argo 实测盐度值的对比结果（图6）可见，DNN 反演数据与Argo 实测盐度值十分接近，均分布在34～36，拟合精度明显高于SSS1 数据。将Argo 数据作为参考标准，计算DNN 模型反演得到的盐度值误差（εDNN=SDNN−SArgo）以及SSS1 产品的误差（εSSS1=SSSS1−SArgo），对比2 种误差（图7）可知：SSS1 产品误差起伏较大，最大误差接近于−4；而DNN 反演盐度数据的误差集中在0 附近，不大于1 且不小于−1，说明其质量明显优于SMOS 数据。此外，SMOS 卫星的SSS1 产品与Argo 实测盐度之间的RMSE 超过0.8，MAE 超过0.5；而DNN 模型反演得到的盐度值与Argo 实测盐度之间的RMSE 为0.249，MAE 为0.193，均明显优于前者。因此，实验结果充分验证了本文方法的有效性和先进性。

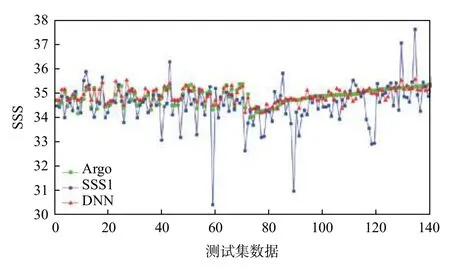
图6 DNN 模型反演盐度、SMOS 卫星SSS1 产品、Argo 实测盐度值对比Fig.6 Comparison of DNN retrieved SSS,SMOS SSS1,and the Argo measured SSS

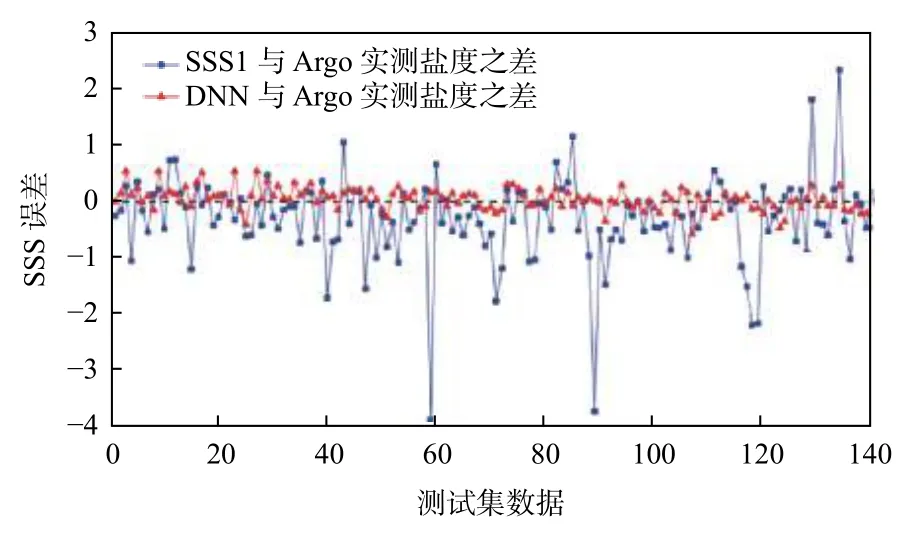
图7 DNN 模型反演盐度与SMOS 卫星SSS1 产品误差对比Fig.7Comparison of errors between DNN retrieved SSS and SMOS SSS1

为验证DNN 模型盐度反演方法的鲁棒性，本文将最佳模型（实验9）重复进行了10 次实验。每一次实验都保证模型参数不变，但随机划分出不同的训练集和测试集数据（保持2 个数据集容量不变），然后验证测试集误差，分别记录每次实验的RMSE 和MAE，并计算出10 次重复实验的平均值（见表4），结果表明：第8 次实验误差最小，其MAE 为0.159，RMSE 为0.195。总体来看，10 次重复实验的平均MAE 为0.216，平均RMSE 为0.262。这10 次训练的差异较小，结果较为稳定，且误差均小于SMOS 卫星盐度产品。因此，本文算法具有较高的鲁棒性。

表4 最优模型10 次实验结果量化指标Table 4 Quantitative indexes of 10 experimental results of the optimal model

5 结论

针对目前SMOS 卫星反演盐度精度未满足预期标准的情况，本文提出了一种基于深度神经网络DNN 的海表盐度反演方法。为避免射频干扰RFI 和银河噪声的影响，研究数据选择了2013 年7 月至8 月太平洋中部海域（150°E～180°，5°～30°N）的SMOS 卫星数据。在建立DNN 模型之前，首先将亮温TB、海表温度SST、纬向风速ZWS、经向风速MWS、有效波高SWH、降雨率RR 和海表蒸发量Eva 共7 个模型输入参数，以及SMOS 卫星3 种盐度产品（SSS1、SSS2、SSS3）和Argo 实测盐度数据，按照空间分辨率为0.5°×0.5°、时间分辨率为36 h 的原则进行时空匹配。然后，将470 组实验数据按照7∶3 比例随机划分为训练集和验证集。在训练集上，采用4 折交叉验证的方式，反复实验，优化模型参数，直至训练出最佳模型。最后，将最佳模型的参数设置固定，进行10 次重复实验，验证了本文方法的鲁棒性。

根据最佳模型的10 次实验表现，DNN 模型反演盐度数据与Argo 实测盐度之间平均MAE 为0.216，平均RMSE 为0.262；最优时，MAE 为0.159，RMSE 为0.195。精度明显高于SMOS 卫星L2 级盐度产品（MAE=0.535，RMSE=0.817）。因此，本文提出算法的反演盐度精度超过了SMOS 卫星盐度产品，且多次实验均取得了较好结果，验证了方法的先进性和稳定性，能够为海洋盐度分析提供较好的数据源，从而有助于推动相关领域的研究进展。