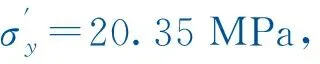高地应力软硬岩隧道初始应力场反演分析

徐 安,全晓娟,汪 波,沈艳芳,谭力豪,谢卓雄

(1.西南交通大学交通隧道工程教育部重点实验室,成都 610031； 2.杭州图强工程材料有限公司,杭州 310006； 3.广东省交通规划设计研究院股份有限公司,广州 510507)

目前，隧道主要以NATM为理念进行设计和施工，为安全高效地施工，需对隧道进行必要的监控和量测，如断面的位移信息[1-2]。大埋深硬岩隧道中，常常也把洞壁二次应力作为主要测试项目，如桑珠岭隧道、苍岭隧道、五女峰隧道、鲍村特长隧道等[3-7]。因此，隧道施工中有大量的现场实测信息。由于大埋深隧道受地形地貌限制，通常无法对初始地应力场进行实测，而初始应力场又是影响长大隧道的主要因素乃至控制性因素。因此，如何有效利用现场实测信息，反演得出初始地应力场等重要参数指标，具有极高的研究价值与工程指导意义。

国内学者已经认识到这一问题，并开展了相关研究。谢学斌等[8]依据沙溪铜矿区的地质资料，采用遗传单纯形算法优化RBF神经网络方法，反演分析出模型区域的岩体力学参数及初始地应力场；夏彬伟等[9]结合渝沙高速共和隧道地应力测量资料，通过调整多种组合的侧压系数，获得了不同测试段地应力，从而展开了岩体地应力反演分析；乔志斌[10]采用基于神经网络替代模型的加速优化算法进行地应力反演，并预测隧道开挖后的岩爆等级；裴书锋等[11]提出了一种考虑地下洞室片帮、钻孔剥落等岩体应力型破坏特征为信息源，通过数值模拟智能反演方法预测高应力大型地下洞室群围岩局部应力场的新思路；张延新等[12]利用水压致裂法实测地应力场来反演初始地应力场；汪波等[13]通过多元回归分析原理结合实测地应力资料反演初始地应力；蒙伟等[14]结合工程实例反演岩体初始地应力场，并分别应用p值法检验、F检验、t检验，验证所采用回归模型和回归系数的显著性和可靠性；唐浩等[15]利用工程类比分析结合构造应力场特征，通过大量试算得到了反演结果。

分析以上研究可以看出，针对不同岩性隧道如何利用实测信息进行分析，尚无深入研究。鉴于此，拟从软、硬岩的工程特性出发，探讨不同岩性隧道的初始应力场反演分析中现场实测信息与方法的合理选择。通过迭代计算，根据相应实测指标反演出与实测洞壁二次应力和位移相符的初始应力边界条件，从而得到依托工程的初始应力场分布特征，并在蒙华铁路软硬岩隧道工程中得到了广泛应用。

1 不同岩性地下工程中应力场反演时实测指标的合理性选择

地下工程中，因地下洞室开挖打破了原有的围岩地应力平衡关系，洞壁切向应力σθ急剧增大，径向应力σr急剧降低(基本为0)(图1)，此时，洞壁围岩由原始的三维应力状态转变为二维应力状态，也即径向约束得到了解除[9]。

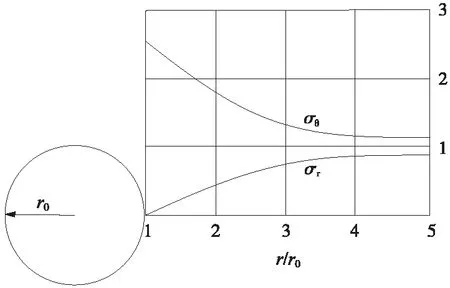
图1 围岩开挖洞壁应力分布

在这种受力状态下，当岩体强度较高时，隧道周边围岩将有可能处于弹性状态；当岩体强度低时，洞室周边围岩进入弹塑性甚至松动状态的可能较大。因此，对于软岩和硬岩隧道而言，虽然洞壁围岩应力状态类似，但因周边围岩状态不同，利用现场实测信息进行初始应力场反演分析时，主要控制指标也应有所差异。

1.1 硬岩地下工程中实测指标选择

硬岩地下工程中因岩体强度较高、岩性较好，隧道开挖后，洞周位移很小，显性表征差，难以通过位移准确反演分析出初始应力场的情况，因此，不能以位移为主进行分析。但硬岩隧道开挖后有一显著特征，那就是围岩产生的弹性变形，也即硬岩隧道开挖后围岩一般处于弹性状态，可根据弹性理论公式得到较为准确的洞壁二次应力值。此时，实测的洞壁二次应力值更具代表性，以洞壁二次应力值为基础反演得出的初始应力场分布特征更为科学、合理[16]，因此，硬岩隧道中建议以洞壁二次应力值作为进行初始应力场反演分析的主控指标。

1.2 软岩地下工程中实测指标选择

软岩隧道相比硬岩隧道而言，隧道开挖后，除产生弹性变形外，洞室周边还将产生一定的塑性变形，在此状态下洞周将产生较大位移，位移的显性表征明显，即在软岩地下工程中产生弹塑性变形条件下，现场监测的位移更具代表性。据此，针对软岩地下洞室的初始应力场反演分析，应以现场监测的拱顶沉降值和拱腰收敛值为主控指标[17]，以现场实测的洞壁二次应力为辅助指标进行。

软、硬岩隧道分化反演流程如图2所示。

图2 初始应力场迭代反演流程

2 不同岩性地下工程中初始应力场反演分析

浩吉铁路是国内最长运煤专线—蒙西到华中煤运铁路，北起内蒙古浩勒报吉站，终至江西省吉安市，线路全长1 837 km。铁路沿线有九岭山隧道、崤山隧道等多条以大埋深硬岩为主的隧道和桐木隧道、条山隧道等多条以大埋深软岩为主的隧道，其中，硬岩隧道围岩大部分以花岗岩为主，软岩隧道围岩主要是千枚岩，地质条件复杂，施工难度较高。现以蒙华铁路九岭山隧道 DK1686+240～DK1687+930段(硬岩隧道段)及桐木隧道DK1705+810～DK1706+448段(软岩隧道段)为例进行工程应用分析。

2.1 硬岩隧道中初始应力场反演分析

浩吉铁路九岭山隧道DK1686+240～ DK1687+930段为花岗岩、花岗闪长岩地层，弱风化，岩质坚硬，岩体较完整，地下水弱发育。埋深约为505 m，总体变化范围不大，并未发现构造应力场。

考虑在该埋深条件下存在高地应力的可能性较大，故在此区段靠近中间位置布设1个地应力测点，测点里程DK1687+240，如图3所示。采用洞壁二次应力解除法，在左边墙处进行应力量测。测点位于左边墙表面处垂直位置，即切向Y方向竖直，如图4所示。

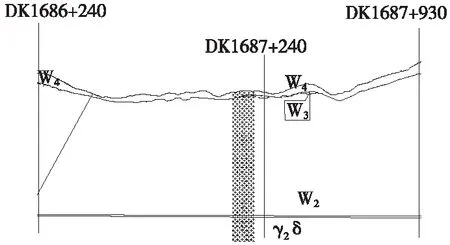
图3 DK1686+240～DK1687+930纵断面

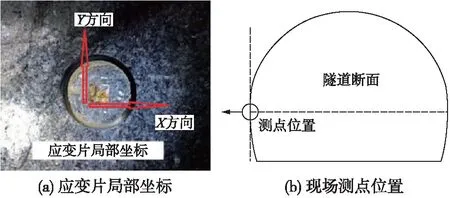
图4 现场测试示意

现场应力解除法获取了测点洞壁围岩约束解除后的应变增量情况，如表1所示。

表1 应力解除法测得应变增量 με

由现场测试数据，经弹性理论公式[11]计算得到洞壁处二次应力，如表2所示。

表2 DK1687+240断面的洞壁二次应力 MPa

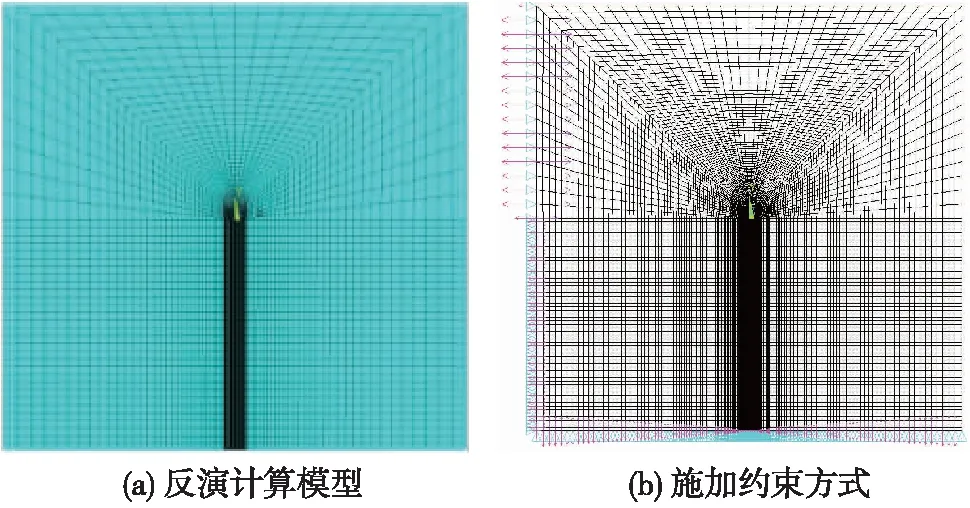
图5 硬岩隧道反演计算模型及约束施加方式

根据浩吉铁路九岭山隧道的实际轮廓建立数值分析模型，如图5所示。通过对表2中洞壁二次应力量值分析可知，σx<σy。由于在无构造应力场情况下，初始应力场类似水压应力场，垂直洞壁的水平径向r方向与轴向x是相同的，即σr<σy，故初步判断初始应力场的侧压力系数“λ<1”。据此，依据弹性力学平面问题的小孔应力公式[18]，得出第一次反演时假定的初始应力边界值[19]，如表3所示。

表3 DK1687+240断面初始反演时应力边界值

根据《九岭山隧道工程地质勘察报告》，结合《铁路隧道设计规范》[20]，确定地应力测试段岩体的物理力学指标，如表4所示。

表4 测试段岩体物理力学指标

依据硬岩隧道初始应力场反演分析流程，得到初始应力边界值下的洞壁切向应力云图，如图6所示。

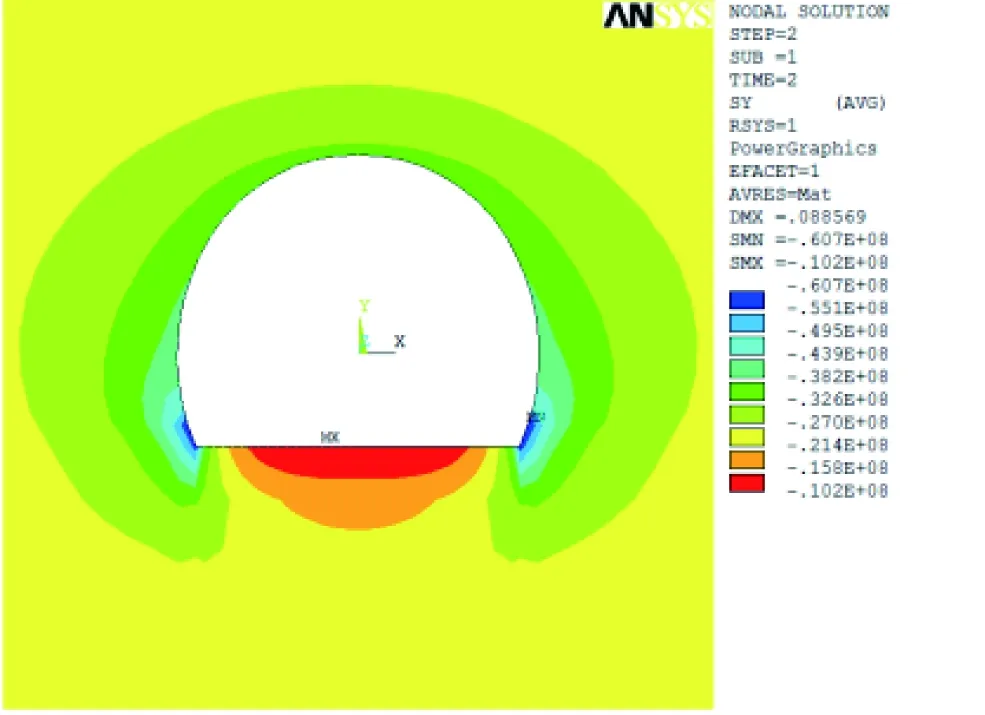
图6 初始应力边界下洞壁切向应力云图(单位：Pa)

从图6可以看出：隧道开挖后，洞壁边墙位置以受压为主，拱脚处小部分区域出现应力集中现象，与现场测试点位置相一致的洞壁处切向应力为41.982 MPa，与实测应力41.360 MPa相比，二者相差约0.622 MPa，差值较小，说明初始反演时拟定的应力边界值较为合理，但仍需作进一步调整。由于切向应力反演值略大于实测值，故逐步减小竖向初始应力值，采用步距为0.05 MPa的等迭代。

按照图2所示迭代反演流程，拟定出后续数值仿真过程，采用等步距迭代，调整迭代计算中相应的竖向及水平初始应力值。迭代反演得到洞壁切向应力仿真计算值，以及与实测值间的差值百分比，如表5所示。

表5 DK1687+240断面迭代反演过程

综合比较分析，迭代步5的反演应力值与现场实测值误差缩小到允许范围内。因此，可近似认为迭代步5下的应力边界条件即为初始应力场。

据此得到隧道DK1687+240断面的初始应力场竖向应力σx=20.35 MPa，水平应力σy=17.908 MPa，侧压力系数λ=0.88。即得到DK1686+240～DK1687+930段的初始应力场分布情况。

结合我国工程岩体分级基准中的高地应力分级标准，该区段面岩石强度应力比σc/σ1=5.23(σc为岩石单轴抗压强度，该区段σc=106.38 MPa)，判别属于高地应力区。以卢森判据、王元汉及王兰生判据为基础[21]，结合现场实测数据及应力判据，DK1686+240～DK1687+930段有可能发生岩爆，等级为轻微岩爆。

2.2 软岩隧道中初始应力场反演分析

桐木隧道DK1705+810～DK1706+448段(图7)为千枚岩地层，岩体强度低，岩质较软，属较软岩地层。埋深约230 m，总体变化范围不大。因该区段隧道断面较小，故未设仰拱。

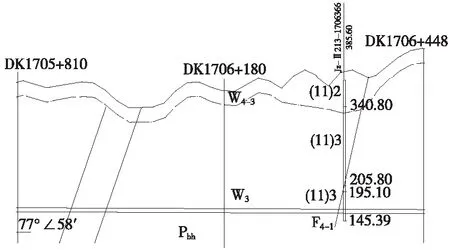
图7 DK1705+810～DK1706+448纵断面

现场应力解除法(同上)测试所得应变增量，如表6所示，利用弹塑性理论公式[22]计算得到洞壁二次应力，如表7所示。

表6 应力解除法测得应变增量 με

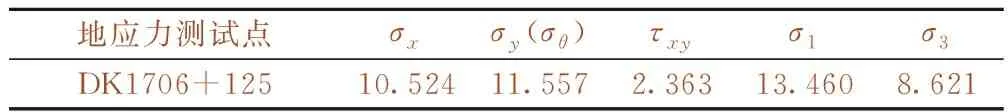
表7 DK1706+180断面的洞壁二次应力 MPa

如前文所述，软岩隧道的反演分析应以位移为主，根据现场的实测信息获取围岩变形全过程位移监测数据，如表8所示。

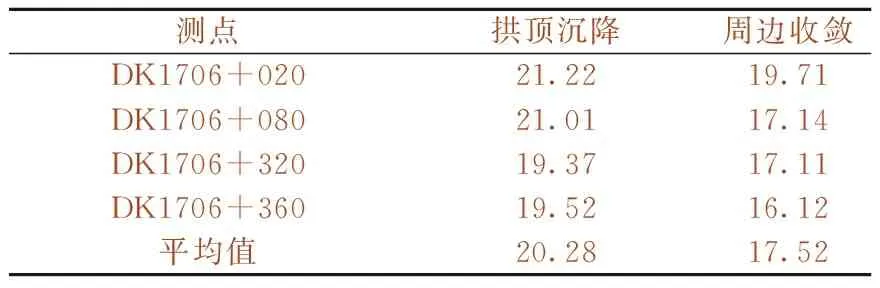
表8 围岩变形监测位移数据 mm

根据软岩隧道的洞室轮廓建立数值分析模型，如图8所示，并初步判断初始应力场侧压力系数λ≈0.86。根据小孔应力公式初步得到初始应力边界值，如表9所示。

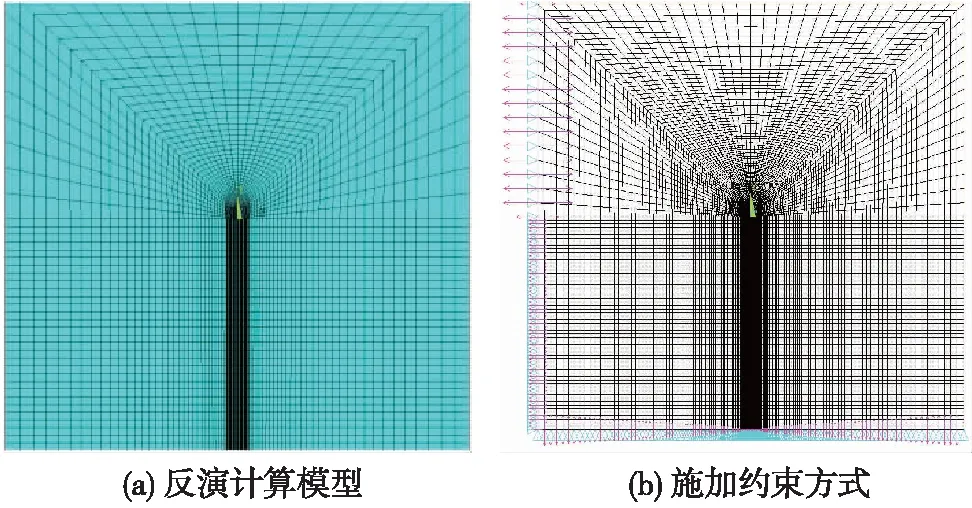
图8 软岩隧道反演计算模型及约束施加方式

表9 DK1706+180 断面初始反演时应力边界值

围岩参数的选取原则同硬岩隧道一致，根据《桐木隧道地质勘察报告》并结合TB10003—2016《铁路隧道设计规范》确定地应力测试段岩体的物理力学指标，如表10所示。

表10 测试段岩体的物理力学指标

依据软岩隧道初始应力场反演分析流程，得初始应力边界值下的洞周位移及洞壁切向应力云图，如图9、图10所示。

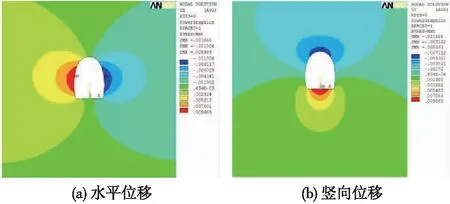
图9 初始应力边界水平(上)和竖向(下)位移云图(单位：m)

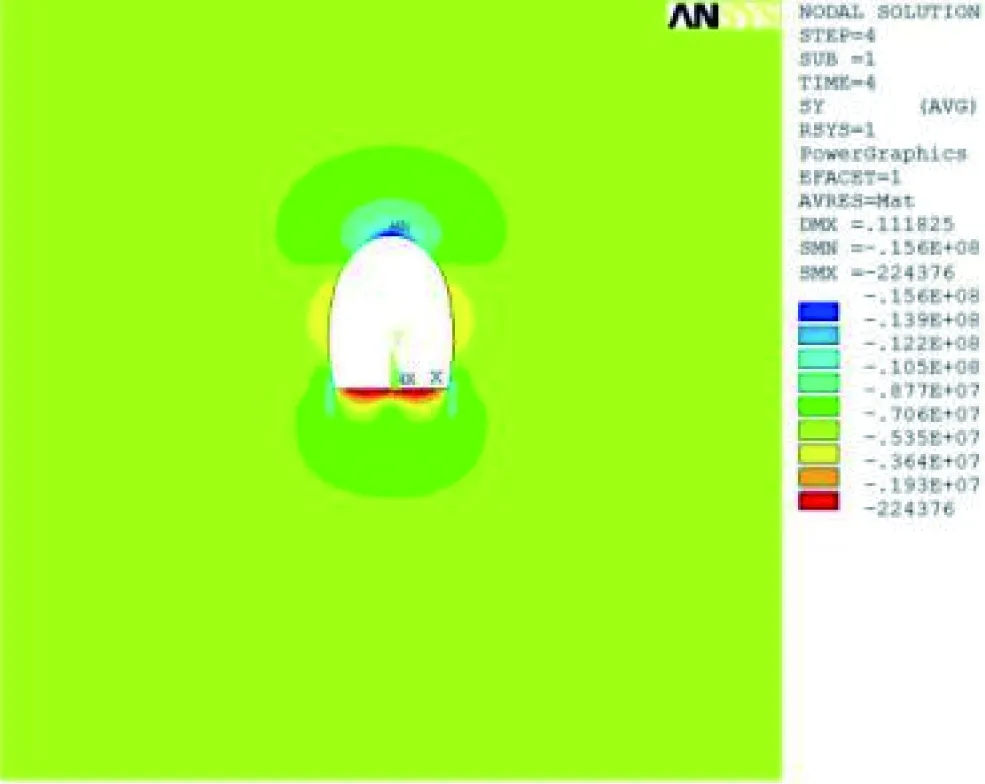
图10 初始应力边界值下洞壁切向应力云图(单位：Pa)

由图9、图10可以看出：隧道开挖后，洞壁周边收敛值为21.49 mm，与现场实测收敛值20.28 mm较接近，但拱顶沉降7.12 mm与现场实测沉降值17.52 mm差别较大，故应调整竖向应力与水平应力比值，即调整侧压力系数λ值；在初始应力边界值下，洞壁以受压为主，边墙监测点切向应力为4.962 MPa，与现场实测应力11.557 MPa二者相差约6.595 MPa，差值较大，说明初始反演时拟定的应力边界值较小，后续计算工况需适当调高应力边界值。根据差值的大小，调整初始竖向应力值为12.374 MPa，λ为0.6，得初始水平应力为7.424 MPa。

在调整后的迭代步2应力边界条件下，洞壁周边收敛为25.21 mm，与实测的洞壁周边收敛值20.28 mm相差较大，而拱顶沉降为18.02 mm和实测沉降值17.52 mm差别较小，故还需继续调整侧压力系数λ；洞壁切向应力值为11.702 MPa，与洞壁实测应力11.557 MPa二者相差约0.145 MPa，差值较小，说明工况2反演时拟定的应力边界值大小较合理，但仍需作进一步调整。采用等步距迭代，逐步减小竖向初始应力。

根据上述分析，调整竖向应力和侧压力系数λ，可得调整后水平应力值。按照迭代参数及其应力边界条件，进行后续应力边界调整，最终得到迭代步7和迭代步8下反演应力值与现场实测值较为符合，如表11所示。但由于软岩条件下，拱顶沉降与拱腰收敛为主要控制指标，而洞壁二次应力为辅助指标，故应优先考虑位移条件。而迭代步8下的反演位移值与现场监测值最为符合，如表12、图11所示。因此，可近似认为迭代步8下的应力边界条件即为初始应力场。

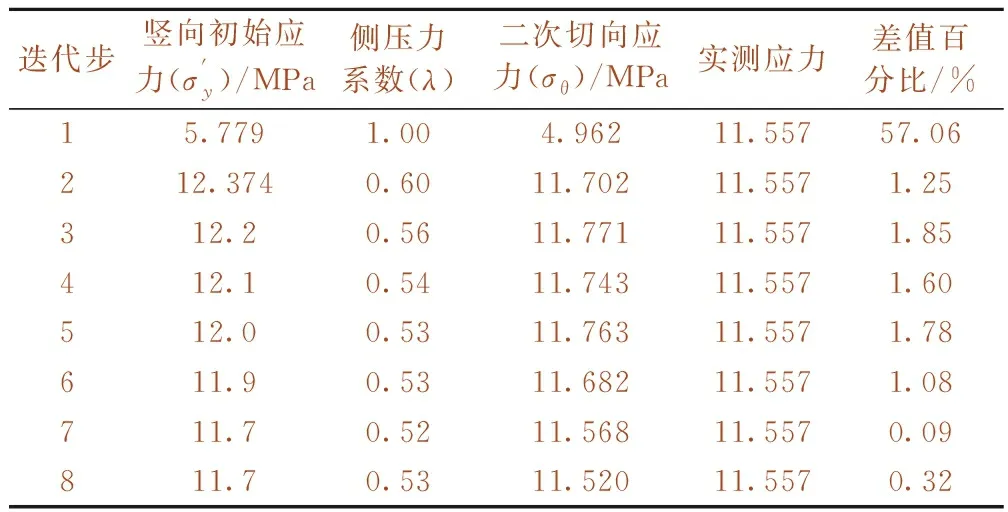
表11 DK1706+180断面应力迭代反演过程

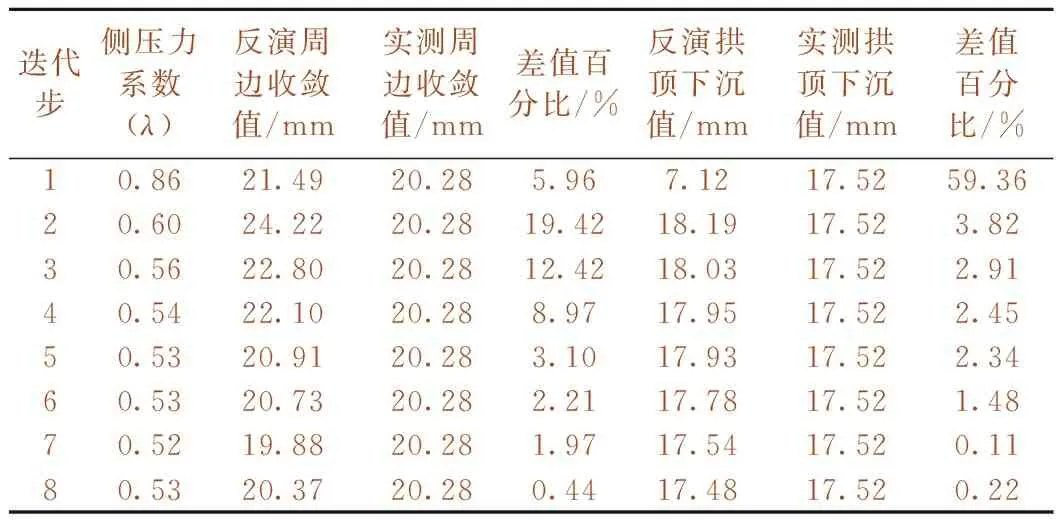
表12 DK1706+180断面位移迭代反演过程

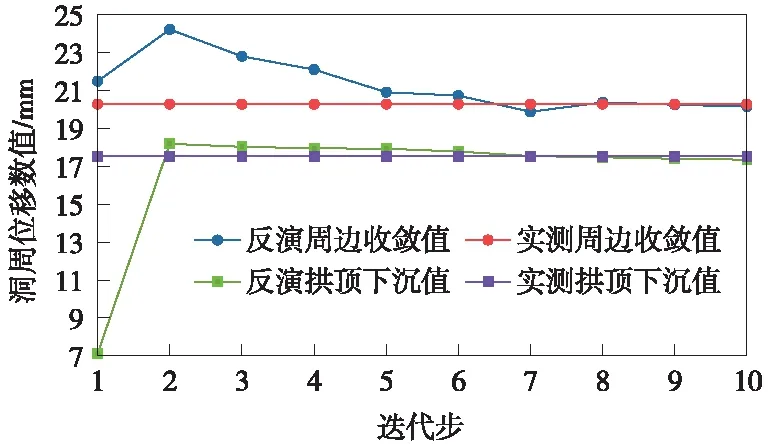
图11 洞周位移反演值与实测值对比曲线

结合我国工程岩体分级基准中高地应力分级标准，该区段面岩石强度应力比σc/σ1=4.30(σc为岩石单轴抗压强度)，判别亦属于高地应力区。

3 结论

通过对软、硬岩地下工程开挖后的洞室应力场及位移场特征分析，结合现场实测信息，提出了基于现场实测信息进行软、硬岩隧道初始应力场反演分析的主控指标及方法，并分别以蒙华铁路软、硬岩隧道为例进行分析，得出以下结论。

(1)从现场实测数据来看，硬岩隧道施工中，洞壁二次切向应力测试非常重要，其直接反映了隧道是否处于高地应力状态以及发生岩爆的可能性和岩爆等级。故硬岩隧道进行初始应力场反演分析时，应以洞壁二次应力测试值为主控指标。

(2)相比硬岩隧道，软岩隧道中位移的监控更为重要，是评判软岩隧道地应力场大小的主要依据。但洞壁二次切向应力测试也不可缺少，是作为评判软岩隧道地应力场大小的参考依据。故软岩隧道初始应力场反演分析时，应以洞周位移为主控指标，洞壁二次应力测试值为辅。