不同速度条件下轨道不平顺分形特征分析

施振青,李再帏,杲 斐,何越磊

(1.上海工程技术大学城市轨道交通学院,上海 201620； 2.中铁二十一局集团有限公司,兰州 730070)

引言

轨道不平顺是导致列车振动的激扰源，一方面影响着列车运行时的安全性和平稳性，另一方面由于轨道不平顺激扰引起的动荷载将加快不平顺的发展，进而加大对列车轨道设备使用寿命和行车安全性影响[1-3]。目前，轨道不平顺评价方法主要有3种：局部不平顺超限评分法、轨道质量指数(Track quality index，TQI)和轨道不平顺谱法[4-6]。这些既有评价方法已形成了相应管理规范，但在铁路线路运营、维护和管理过程中，列车运行平顺性问题仍是养护维修中需解决的核心矛盾[7]。不同线路运营条件下，轨道的不平顺和空间频率都不相同，引起列车的动态响应也不同；另外，列车在不同速度等级运行状态下，车体振动剧烈的频段范围也不同[8-10]。因此，针对目前TQI普遍优秀现状，如何更为有效地实现轨道平顺状态评估，是现代铁路轨道管理中必须解决的关键问题[11]。

随着近年来非线性科学的快速发展，分形理论作为一种高效方法在国外铁路轨道管理中得到了应用，取得了一定的管理效果。LANDGRAF[12]分析了奥地利铁路近十年轨道高低不平顺样本数据，提出采用分形理论可以说明道砟劣化问题，且不同波长区间内高低不平顺的分形特征也不同；TACIROG LU[13]对土耳其高铁轨检数据进行分析，提出4种不同分形维数来确定轨道不平顺，并讨论了分形维数与TQI之间的关系；HYSLIP[14]中采用尺码法计算了高低不平顺分形维数特征，并应用于美国铁路FRA的管理中。我国学者则着重讨论了钢轨波磨等短波长不平顺的分形维数特征，赵国堂[15]讨论了钢轨波磨的分形特征，将分形维数作为波磨分类的指标；伍曾[16]对实测波磨痕迹曲线的分形维数进行计算，讨论了轨道各构件动力响应与波磨分形维数之间的关系；陈光雄[17]根据功率谱指数与分形维数的关系，计算了不同实验条件下波状磨耗的分形维数。

已有研究深化了轨道不平顺多层次认识，为轨道平顺性管理提供了新的发展思路。但同样值得注意的是，由于目前线路运营速度众多，各个速度下轨道不平顺分形维数尚缺乏针对性分析与比较，不利于构建统一的轨道平顺性管理理论与方法。基于此，综合现有研究成果基础上，采用尺码法计算轨道不平顺分形维数，讨论不同运营速度下轨道不平顺的分布特征，确定分形维数变化规律，为深化轨道平顺状态控制方法奠定基础。

1 尺码法原理

一般而言，可采用分形维数来表征轨道不平顺的实际状态[18]，而尺码法是目前被用于计算轨道不平顺分形维数的常用方法[13]。

尺码法是用不同长度的标尺测量不平顺幅值图案的长度，以计算幅值曲线图案的分形维数，可定量化的表征结构复杂性或粗糙度。长度不断变化的标尺会逐步在不平顺幅值曲线上移动，每移动一次与幅值曲线相交1个点。只需将尺码长度(λ)乘以步数(N)，再加上剩余长度f，即可计算出不平顺幅值曲线的总长度(L(λ))。

L(λ)=λ(N+f/λ)

(1)

随着测量过程中使用标尺的尺码长度减小，尺子在更多点处与不平顺幅值曲线相交，且测量精度提高，所测量不平顺幅值曲线的总长度也会增加。为协调总长度，式(1)中引入幂指数D，对于给定的尺码长度(λ)

L(λ)=λD(N+f/λ)

(2)

将式(2)改写为Lλ-D=N+f/λ，幂指数可利用对数法则导出它的求解公式，将式(2)等式两边同时取对数

lg(N+f/λ)=-D(lgλ)+lgL

(3)

式(3)有y=kx+b形式，给定不同的尺码长度λ来测量一条线的长度，然后绘制图lgλ和lgL(λ)，通过使用趋势线斜率k，用最小二乘线性回归分析求出未知数，来计算不平顺幅值曲线的分形维数(D)值，k与D关系为

D=1-k

(4)

上述方法的计算流程如图1所示。

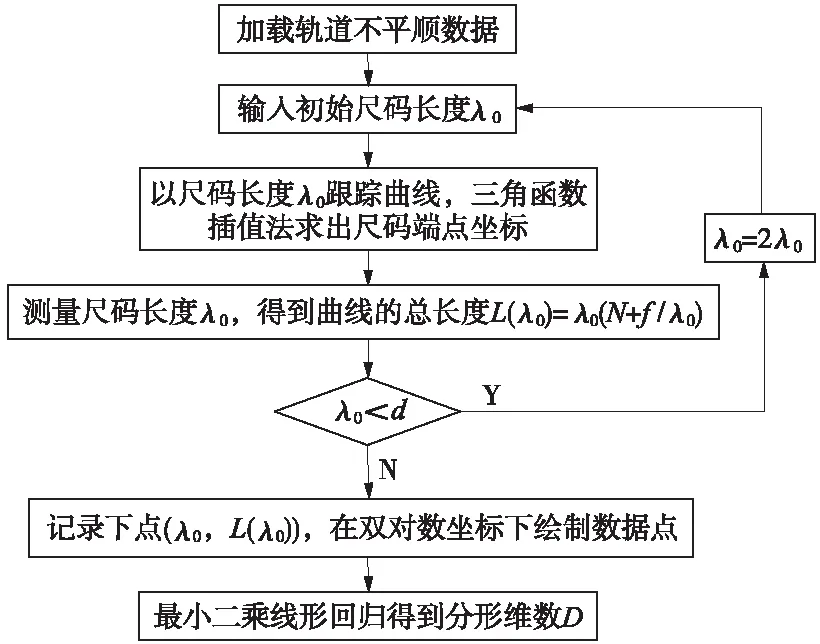
图1 尺码法计算流程

2 分形特征分析

2.1 样本来源

轨道不平顺数据来源为轨道综合检测列车检测结果。由于列车垂向和横向振动的主要激扰来源为高低不平顺和轨向不平顺[19]，因此，将这两种轨道不平顺作为分析对象。为对比分析不同速度因素的影响，结合线路运营状态，分析了4种线路轨道不平顺数据，基本情况如表1所示，数据样本采样时间均为2021年3月，样本长度为100 km。

2.2 高低及轨向不平顺分形维数

轨道不平顺波长具有一定的分形维数特征，借助Matlab软件，采用左高低、左轨向不平顺数据样本说明尺码法的测量过程，2种样本的幅值分布如图2所示。

表1 样本类型

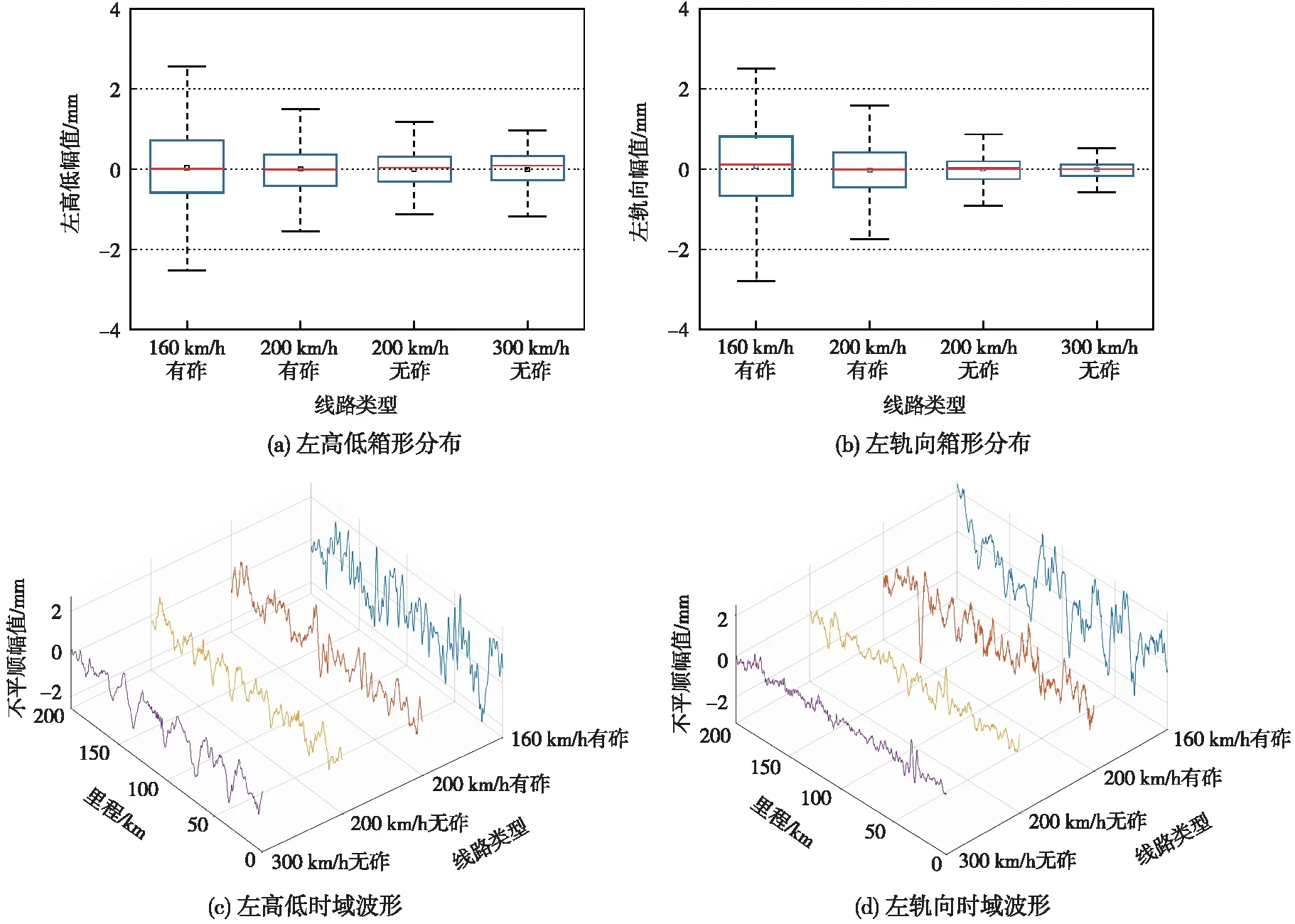
图2 不平顺数据样本

由图2可知，随着列车速度增加，轨道不平顺幅值逐渐减小，且均符合幅值管理I级指标；同一速度条件下，无砟轨道平顺性状态较有砟轨道好。运营速度为300 km/h样本下线路平顺状态最好。

将这些数据采用尺码法进行计算，以初步说明轨道平顺性状态的分布特征，图3、图4分别为左高低和轨向不平顺的计算结果。

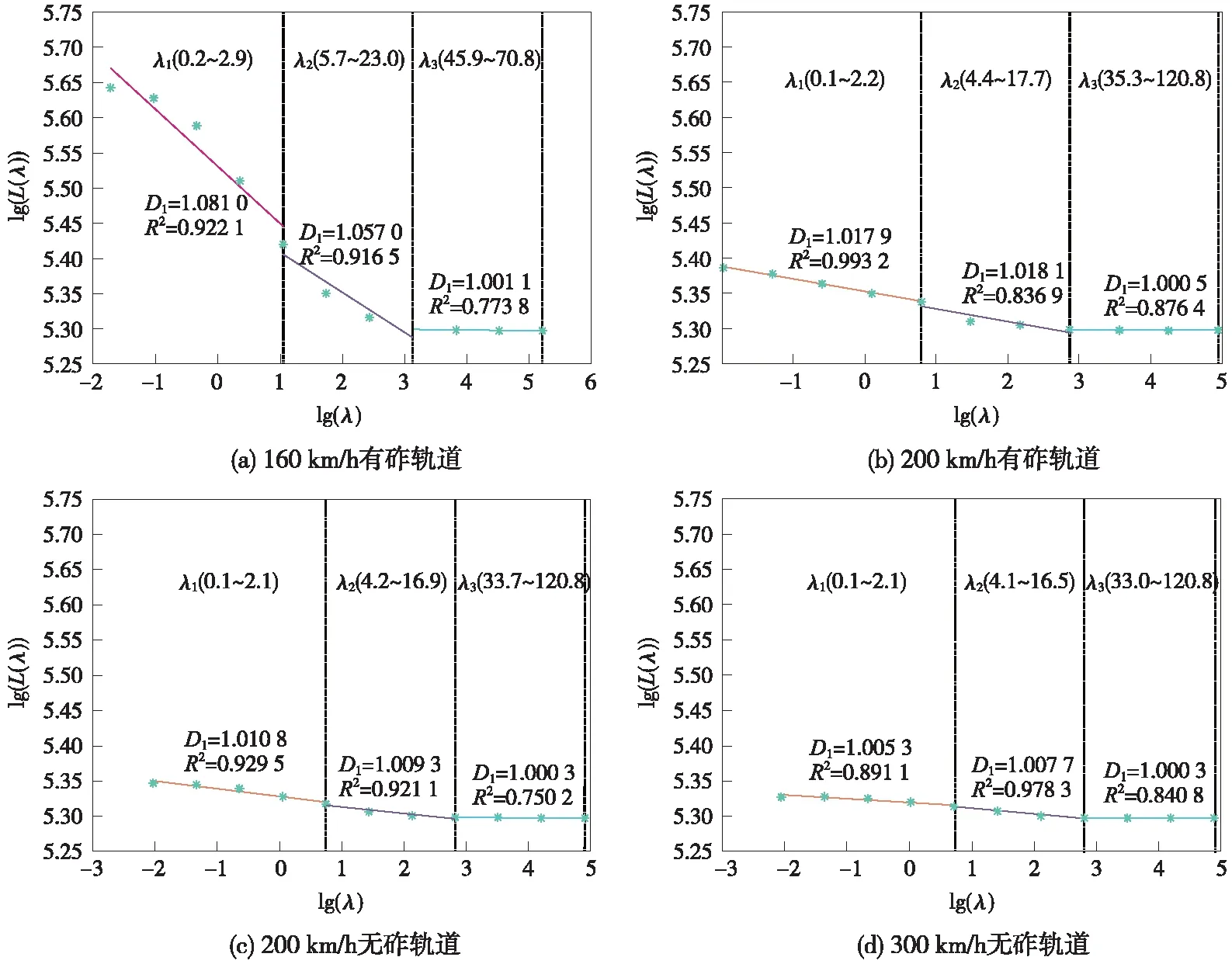
图3 左高低分形维数

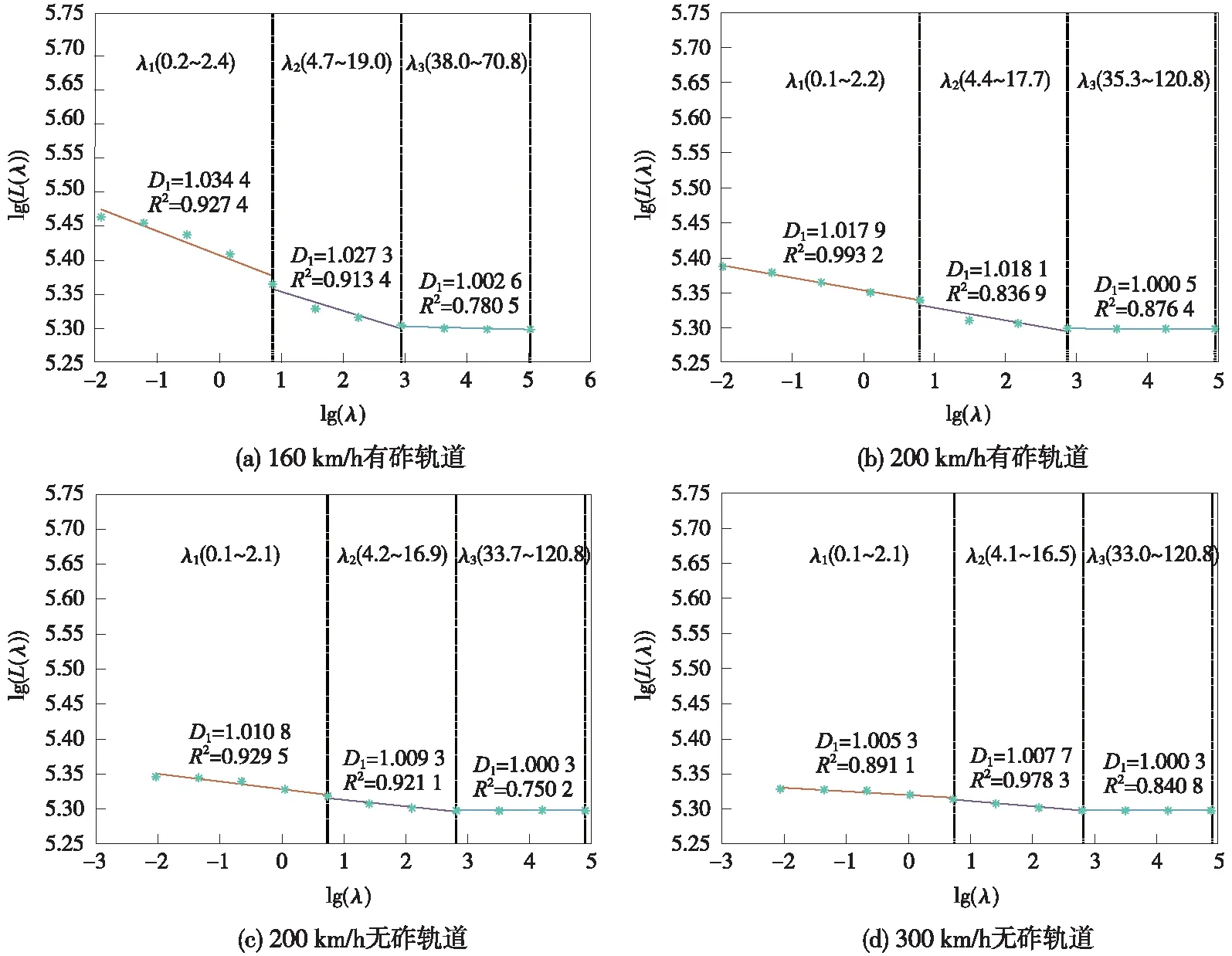
图4 左轨向分形维数

由图3可知，得到的轨道不平顺分形维数存在明显分段“台阶”特征，无法用统一的分形维数来表征轨道不平顺空间特征，这与国外研究结论[5-7]相类似，故本研究利用三段式分析，通过2个分割点来分别提取3个波段的分形维数特征。由于行车速度对敏感波长影响较大，随着行车速度增大，各阶敏感波长出现“频移现象”，具体表现为行车速度越大，敏感波长越小[20]。根据轨道不平顺的实际分布特征，结合分形维数双对数图，选取波长为5，30 m左右2个分割点，分波段提取分形维数特征。不同运营速度下高低不平顺的波长区间存在一定差异性，且各区间分形维数也呈现了不同的特征，既有提速干线的λ3长波区段相对较短，而运营速度200 km/h及以上的高速线路则稳定在120 m左右。

对比3个区间的分形维数值可知，运营速度在200 km/h及以上的高速线路分形维数差异性较小，总体上随运营速度增加，D1值由1.081 0递减为1.005 3，D2值由1.057 70递减为1.007 7，D3值由1.001 1递减为1.000 3，分形维数逐渐减小，但减小程度较轻，说明现有高速铁路线路的质量状态较为稳定，在无显著病害条件下，不会产生剧烈变化。而160 km/h干线线路，由于客货混跑，线路通过总重大，有砟轨道状态呈现一定的劣化，分形维数则显著地增大。这也更为显著地表明速度等级越高，线路平顺性状态越好，不平顺幅值变化更为规则，分形维数则越小。

由图4可知，不同运营速度下轨向不平顺与高低不平顺的分形维数分布整体规律类似，但高速铁路有砟轨道与既有干线有砟轨道状态差异性较小，而无砟轨道与有砟轨道差异性显著。说明正常运营条件下，无砟轨道的分形维数应较为稳定，不会产生明显变化，这是由无砟轨道结构整体刚度大、结构累计变形(路基工后沉降、路基与桥涵等结构过渡区域差异沉降、无砟轨道及桥梁等工程结构变形)小的特点所决定的。

综上可知，轨道平顺性特征可通过分形维数来表征，此种方式即可表征相应的波长区间，又可以实现波长区间的定量化评价，这无疑为轨道平顺性评估提供了一种新的思路。

2.3 分形维数量值分析

为进一步说明分形维数量值范围，是否存在区间固定值，初步计算了表1中100 km线路高低及轨向不平顺检测数据，计算区段长度200 m，则500次计算结果如图5、图6所示。

图5 左高低分形维数对比

图6 左轨向分形维数对比

由图5、图6可知，无砟线路各波长区间的量值呈现窄带分布，极值范围不大；而有砟线路则相对幅值范围较宽，即无砟轨道波长维数量值稳定性高于有砟轨道，且既有干线铁路离散性最大，高于200 km/h有砟线路。这说明轨道结构刚度对于分形维数量值有一定影响，对于量值较为稳定的无砟轨道而言，各波长区间分形维数可作为发现结构病害的有效手段，特别是分形维数短时间内产生显著变化时，说明无砟轨道区段存在着一定病害，这也为充分利用海量轨检数据提供了新的途径。

3 结论

(1)几何分形方法从幅值和波长2个角度有效地表征了轨道平顺性状态；利用尺码法计算轨道不平顺分形维数可得到三段式结果。

(2)不同运营速度对于分形维数的波长和幅值区间有一定影响，既有干线线路分形维数值最大，300 km/h无砟线路分形维数值最小。

(3)运营速度增加，线路条件变好，分形维数λ1区段缩短，λ3区段范围增大。

(4)无砟线路分形维数值呈现窄带分布，建议采用分形维数指标对无砟轨道服役状态进行管理，并进一步的积累数据特征，为深化和健全铁路线路养修管理奠定技术基础。