基于粘结滑移的衬砌裂缝宽度计算模型研究

贺 欢

(中国电建集团中南勘测设计研究院有限公司，长沙 410014)

1 研究背景

输水隧洞由于结构所受荷载的多样性和复杂性常常出现裂缝，裂缝的存在危害隧洞的安全稳定运行，因此隧洞衬砌裂缝一直是研究关注的重点。隧洞衬砌与围岩联合受力的特点，完全不同于独立承载的钢筋混凝土梁、板、柱结构。衬砌一旦开裂，与围岩接触面的应力产生重分布，将显著改变衬砌裂缝的变化特性[1]。由于开裂机理的复杂性和裂缝生成的随机性，关于衬砌裂缝宽度的计算尚无定论。

佘磊等[2]对现有国内外钢筋混凝土衬砌裂缝计算公式进行了综述。这些计算公式大致分为两类[3]：一是基于裂缝开展机理推导理论公式再用试验资料确定计算系数的半理论半经验公式；二是根据大量实测资料采用回归分析法分析不同参数对裂缝开展宽度的影响程度。两类计算公式都需要求解受力钢筋应力，而隧洞由于围岩压力和内外水压力作用、混凝土开裂非线性等因素，使得采用简化的解析法计算钢筋应力存在一定困难与偏差，特别是对于非圆形断面隧洞非对称分布力学模型，解析法更是难以求解[4]，因此一些研究者开始研究有限元数值解法。

现有研究对于钢筋-混凝土粘结滑移效应的模拟常运用弹簧单元[5]，但钢筋为线级图元而混凝土为体级图元，导致网格划分后需要建立弹簧单元节点对的方向错综复杂，使得建立指定受力方向的弹簧单元难度骤增，甚至根本无法实现。为解决此问题，本文基于粘结滑移理论提出了一种“实体单元-影子节点-梁单元”的传力体系来模拟衬砌混凝土和钢筋的传力特性。根据某一隧洞模型试验建立了有限元模型，将钢筋混凝土衬砌分离式建模并构建上述传力体系。通过有限元计算求得钢筋应力，结合规范公式计算裂缝最大宽度。将计算结果与试验结果进行对比，验证了此传力体系的可行性。该传力模型有效解决了钢筋单元与衬砌单元之间建立指定受力方向弹簧单元的困难，可为类似工程最大裂缝宽度计算提供参考。

2 试验内容

为分析水工隧洞衬砌开裂特性，进行限裂设计研究，某单位开展了大比尺水工隧洞模型试验[6]。该隧洞有限元整体模型尺寸为 6.5 m×5.5 m×5.7 m，C20混凝土衬砌，内径 0.8 m，外径 0.92 m，厚 0.06 m，分为A与B两部分，A部分双层配筋，B部分单层配筋。环筋Φ8@100，直筋8Φ8，保护层厚度7 mm，衬砌配筋截面如图1所示。

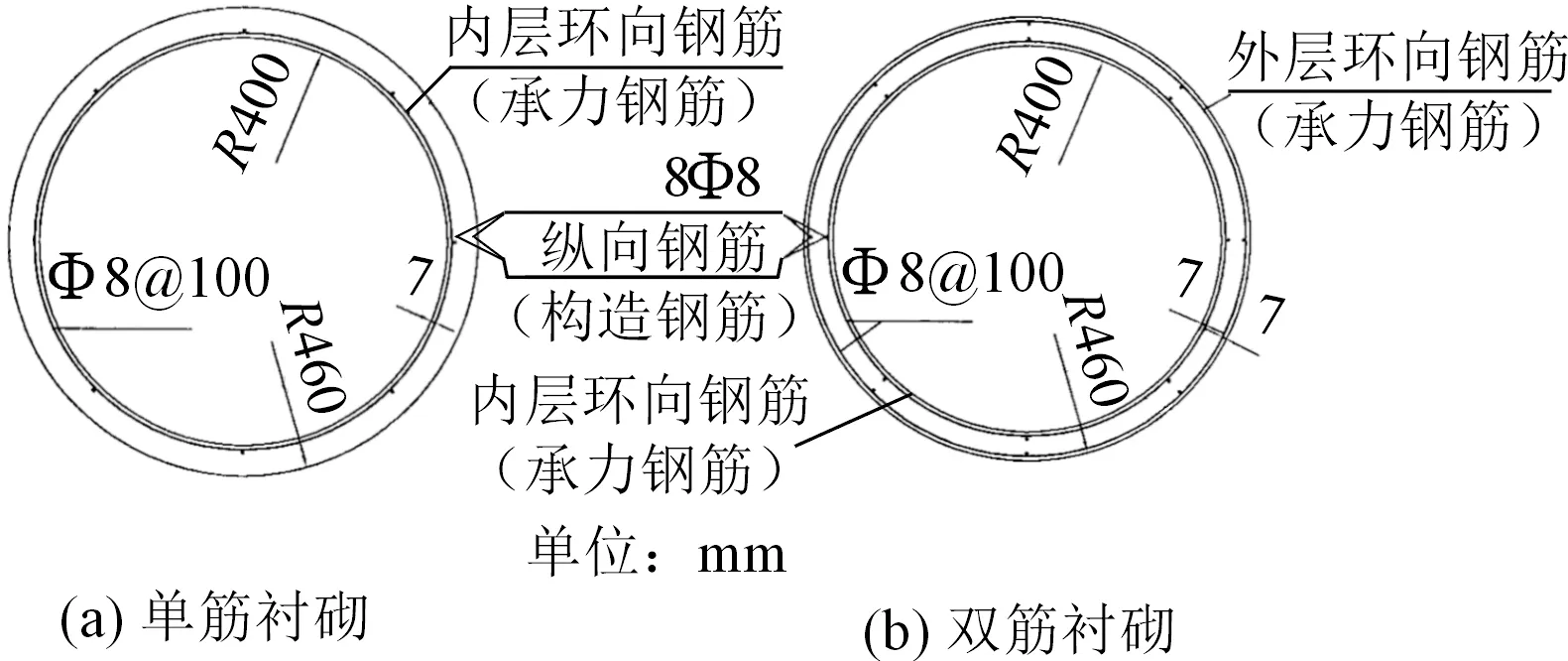
图1 单、双筋衬砌截面图Fig.1 Schematic diagram of tunnel sections with single-layer and dual-layer reinforced concrete lining

材料的力学参数如表1所示，模型细部尺寸、试验过程及试验结果等其他内容都参考文献[7]。

表1 材料参数Table 1 Parameters of materials

3 有限元建模

3.1 计算模型与过程

(1)有限元整体模型尺寸(Z轴方向只截取了1延米)如图2所示。

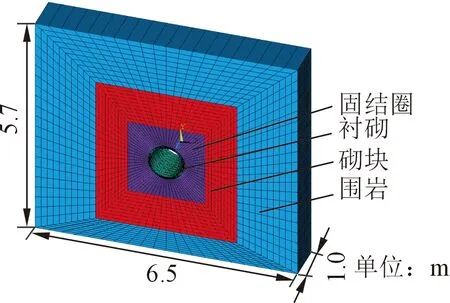
图2 有限元整体模型Fig.2 Finite element model

(2)位移约束：根据试验情况可知模型位移约束为底部固结全约束，两侧法向约束。

(3)计算步骤：第一步施加重力计算；第二步重启动分析后，施加1.70 MPa的内水压力，分17个荷载子步计算，即每个荷载子步的内水压力增量为0.1 MPa；以模拟试验初次充水工况的全过程。

(4)开裂处理：通过实体单元定义混凝土材料参数模拟衬砌混凝土的非线性开裂。将单、双筋衬砌开裂位置的小部分实体单元抗拉强度进行折减，单元强度弱化处理来模拟预留裂缝，减少试验结果不对称的影响，与试验结果更好地拟合。

3.2 传力体系

本文所述“实体单元-影子节点-梁单元”的传力体系的构建方法是将模拟钢筋的梁单元对应的节点在其原位置复制一份为游离的影子节点，将影子节点作为衬砌混凝土和钢筋的传力媒介。衬砌实体单元和影子节点之间建立同一约束方程使其变形协调，影子节点与钢筋梁单元之间建立三向组合弹簧，通过组合3个方向的单轴弹簧单元模拟粘结滑移效应，如图3所示。

图3 传力体系示意图Fig.3 Schematic diagram of the force transmission system

3.3 组合弹簧

如图4所示，采用的三向组合弹簧分别为柱坐标系下的r、θ、h(对应笛卡尔坐标系X、Y、Z)方向，kr、kθ、kh分别为柱坐标系下X、Y、Z方向的弹簧刚度。弹簧刚度kθ的粘结力F-滑移量D曲线根据《混凝土结构设计规范》[8]给出的钢筋粘结应力-滑移(τ-S)本构关系曲线转化得到，即

图4 组合弹簧示意图Fig.4 Schematic diagram of combined spring

F=τS。

(1)

式中：τ为钢筋粘结应力；S为每个梁单元的侧面积。通过控制直筋和环筋的单元划分份数将每个梁单元的长度ξ定为0.02 m，则由钢筋直径d和梁单元的长度ξ表示F为

F=τπdξ。

(2)

计算可得弹簧受拉的F-D曲线如图5所示。F的单位为N，而滑移量D的单位为mm，受压曲线定义为受拉曲线的镜像。

图5 弹簧刚度F-D曲线Fig.5 Curves of F versus D of spring rigidity

根据钢筋的滑移方向可知环筋θ方向和直筋h方向的弹簧为可产生滑移的弹簧，kθ即为上述F-D曲线的斜率。而另外2个方向不产生滑移，即无应变变形，可通过将其刚度取一极大值来实现。本文将其定义为kθ的106倍。

4 计算结果

4.1 钢筋应力

有限元计算结果输出梁单元的轴力N，通过钢筋的截面尺寸(直径d为8 mm)换算可得钢筋应力为

(3)

试验中测有裂缝宽度结果的开裂位置是单筋衬砌内侧45°和180°以及双筋衬砌内、外侧90°和225°。衬砌开裂情况计算结果如图6所示。

图6 衬砌开裂示意图Fig.6 Schematic diagram of lining crack

计算值的内水压力为0.1 MPa整数倍的有限元计算结果，其他结果通过插值得到。其钢筋应力-荷载关系的试验和计算结果对比如图7所示。

图7 钢筋应力-荷载关系曲线对比Fig.7 Comparison of stress-load curves between dual-layer and single layer reinforcements

整体计算结果的钢筋应力随内水压力增大而增大的变化趋势正确，部分结果如双筋衬砌90°位置内、外筋应力结果拟合较好，在1.0～1.3 MPa起裂荷载的应力结果拟合较好，总体误差较小。而部分结果如双筋衬砌225°位置内、外筋应力结果和单筋衬砌180°位置内筋应力结果拟合不好，荷载>1.3 MPa以后计算与试验结果存在较大偏差。这一偏差主要来源于试验衬砌开裂位置的贯穿裂缝发生了内水外渗导致该处受到未知大小的外水压力作用。试验过程中也发现贯穿开裂导致法兰盘漏水而无法再增大内水压力的情况。衬砌内、外水压差降低，导致衬砌的拉应力降低，使得钢筋拉应变在内水压力增大的过程中出现“回缩现象”，钢筋应力反而减小，出现与计算结果的偏差。

从图7的结果可知双筋衬砌内、外侧90°和单筋衬砌内侧45°拟合结果很好，而双筋衬砌外侧225°和单筋衬砌内侧180°拟合结果较差。在1.0～1.3 MPa内水压力荷载作用的起裂初期拟合结果都比较好，说明在没有渗漏导致的外水压力作用的影响下，有限元建模构建这种传力体系计算衬砌混凝土中钢筋的应力是合理有效的。

4.2 最大滑移量

弹簧两端节点的位移差表征钢筋的滑移量，每个荷载子步最大滑移量的计算结果如表2所示。

表2 最大滑移量计算结果Table 2 Calculation results of maximum slip deformation

可以看出在内水压力荷载较小的加载初期，钢筋最大滑移量均较小，处于0.1 μm数量级，说明在开裂前，钢筋与衬砌混凝土粘结良好近似无滑移。内水压力加载到1.0 MPa时，单、双筋衬砌钢筋最大滑移量均增加了2个数量级，说明起裂后钢筋与衬砌混凝土不再紧密粘结，钢筋发生较大滑移。单筋衬砌钢筋最大滑移量为0.021 4 mm，双筋衬砌钢筋最大滑移量为0.022 6 mm。

4.3 衬砌承载比例

衬砌结构受力示意如图8所示。

图8 衬砌结构受力示意简图Fig.8 Schematic diagram of forces acting on lining structure

衬砌承载比例为衬砌混凝土和钢筋承担的内水压力荷载比例。沿水流方向取长度L为0.1 m，则有结构x方向受力平衡，即

(4)

式中：F岩x为围岩压力水平X向分力；Px为内水压力水平X向分力；r为衬砌半径，取0.4 m。

通过有限元计算得出0°与180°两个截面的衬砌混凝土与环筋的拉力，即可求出衬砌承担内水压力的比例，有限元计算结果与试验结果对比如表3所示。可得知模型计算得到的承载比例结果较好，钢筋混凝土传力模型能比较有效地模拟衬砌承载过程，说明通过这种有限元模型计算衬砌承受外荷载比例的方法是可行的，计算结果具有一定参考价值。

表3 衬砌承载比例计算结果对比Table 3 Comparison of load bearing proportions between dual-layer and single layer reinforcements

4.4 最大裂缝宽度

利用《水工混凝土结构设计规范》[9]公式计算最大裂缝宽度ωmax，即：

(5)

(6)

式中：α为考虑构件受力特征和荷载长期作用的综合影响系数，轴心与小偏心受拉取2.7；σs为有限元计算得到的衬砌开裂后最大钢筋应力；Es为钢筋弹性模量，取210 GPa；c为最外层纵向受拉钢筋外边缘至受拉区边缘的距离，取7 mm；d为钢筋直径，取8 mm；As为有效受拉混凝土截面面积，取洞内1延米计算；Ate为受拉区纵向钢筋截面面积，取洞内1延米计算；ρte为纵向受拉钢筋有效配筋率，最小值为0.03，可求出单、双筋衬砌配筋率均<0.03，故取0.03。

各开裂位置的最大钢筋应力计算结果与通过公式求得的最大裂缝宽度和试验值对比结果如表4所示。

表4 衬砌最大裂缝宽度计算结果对比Table 4 Comparison of calculated maximum crack width of lining between dual-layer and single layer reinforcements

双筋衬砌最大裂缝宽度计算结果略大于试验值，单筋衬砌最大裂缝宽度计算结果小于试验值，双筋衬砌计算结果更好。整体计算结果与试验值同数量级，计算误差相比文献[1]和文献[7]的裂缝宽度计算方法更小。可认为此种最大裂缝宽度计算方法是正确有效的。

5 结 语

文章提出并论述说明了“实体单元-影子节点-梁单元”的传力体系。基于某一隧洞模型试验的试验结果，将钢筋分离式建模并利用此传力体系构建了“实体-弹簧-梁”的钢筋混凝土传力模型。通过有限元计算得到衬砌钢筋的应力与最大滑移量、衬砌承载比例和最大裂缝宽度的计算结果并与试验结果进行了对比，分析了偏差主要来源于渗漏导致的外水压力。整体计算结果与试验结果拟合较好，说明文章所提出的这种基于粘结滑移的衬砌最大裂缝宽度计算方法是正确有效的。研究成果为钢筋混凝土衬砌结构最大裂缝宽度建模计算提供了一种新的方法，并可推广到其他同类工程，特别是对于解析法存在困难的非圆形断面隧洞。