基于组合权重的模糊物元模型在输水管材选型中的应用

郭明杰，胡少伟，单常喜，薛 翔，李 江

(1.重庆大学 土木工程学院，重庆 400045； 2.新疆水利水电规划设计管理局，乌鲁木齐 830000)

1 研究背景

在大量的输调水管道工程事故中，管材选择不当造成的事故占相当大的比例，因此，管材的合理选用尤为重要[1-2]。在输调水工程中，管材类型的选用要根据管材的技术特性和工程条件的勘察结果，通过技术、经济、安全等方面的论证综合比较，择优选择管材[3-4]。我国地域辽阔，各地区的自然状况、地形地质、经济形势不同，且每项工程都具有特殊性，导致输调水工程管材的应用也不尽相同。因此，如何客观地根据工程规模、管材技术特性和使用条件等多方面科学合理地进行输水工程管材经济、技术、安全的综合比选，一直是设计人员及决策人员面临的技术难题。研究输调水工程管材选型问题，对节省工程投资、提升工程质量、保障运行安全具有十分重要的意义[5]。

Zhao等[6]在绿色设计背景下，利用多属性决策方法研究了3种材料在管道设计中的适应性选择；令志强等[7]结合喀斯特山区供水管网设计建立了评价矩阵，结合价值工程进行管材选择；陈莹等[8]根据技术经济学理论从技术经济评价角度选取水文水井成井管材；Alberto等[9]讨论管道材料适用性、管壁厚度、浪涌保护和瞬态压力等进行了输水干管的管材选择；Giaccobi等[10]将生命周期评估法与层次分析法相结合，分析了建筑给排水中管材的适宜性评价选择；Anojkumar等[11]利用FAHP-TOPSIS等4种多准则决策方法解决制糖业管道材料选择问题；徐飞飞等[12]针对某支线输水工程，利用模糊数学综合评价法进行管材选型；王蒙[13]利用层次分析法和模糊评价法对农田灌溉工程进行了管材选型；张继明等[14]利用熵权与层级分析法对机械臂设计方案进行了选择研究；郭文献等[15]基于变异系数权重，利用模糊评价模型进行了节水灌溉方式的选择研究。目前对于输水管材的选型、经济性分析进行了大量研究。但这些研究大都停留在对于某个具体工程案例的选管分析或者对于常用管材的调研和能力评价阶段，且评价指标体系也不尽完善。目前缺乏一种广泛适用的输水管材的优选方法来指导工程设计人员对工程项目的实际情况进行管材选型。

本文在模糊物元分析理论的基础上，分析了影响管材选择中的各种指标和因素，构建了一套较为完善的管材类型选择的综合评价指标体系，同时改进了传统的权重确定方法，提出了使用层次分析法和变异系数计算各影响因素的组合权重，并利用欧氏贴近度结合价值工程方法判断最优管型，建立基于组合权重的模糊物元模型，为输调水管道工程的选材提供了一种更加合理、科学的评价方法。

2 模糊物元模型

2.1 复合模糊物元概念[16]

模糊物元分析中研究对象M及其特征C和量值x组成的物元R=(M，C，x)，矩阵形式记作

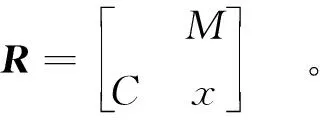
(1)

式中：R表示模糊物元；M表示对象；C为对象M的特征；x表示与特征C相应的隶属度。

对于输调水工程中管材选择而言，M就是管材类型；C是评价指标；x是评选方案M对评价指标C相应指标值的隶属度。

若管材选择类型M有n项评价指标C1，C2，…，Cn，与其相对应的模糊量值x1，x2，…，xn，则称R为n维模糊物元。若以Rnm表示m种管材类型n维复合模糊物元，并以Mj表示第j个评选方案(j=1，2，…，m)，Ci表示第i个评价指标，对应的模糊量值为x1，x2，…，xn，xnm表示第m个评选方案对第n个评价指标相应指标值的隶属度，则有

(2)

2.2 从优隶属度原则

模糊物元各评价指标相应的模糊量值，从属于标准方案中各对应指标相应模糊量值的隶属程度，称为从优隶属度[17-18]。对越大越优型指标，采用

(3)

对越小越优型指标，采用

(4)

式中minxij、maxxij分别为各事物中第i项特征所对应的所有量xij中的最小值和最大值。

(5)

2.3 标准模糊物元与差平方复合模糊物元

(6)

3 组合权重和综合评价

为了在主观赋权的基础上得到更具有客观性的权重，本文通过采用变异系数法和层次分析法分别计算各因子对管材选择的组合权重[20]，引入了变异系数法修正层次分析法确定指标权重时的主观性，并利用欧式贴近度结合价值工程原理判断最优管型。

3.1 变异系数法确定指标权重

采用反映评价指标特征值之间关系的参数——变异系数作为客观因素的评价指标，其计算公式如下：

(7)

(8)

(9)

(10)

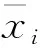
由此可构造各评价指标权重复合物元Rw，即

(11)

3.2 AHP法确定指标权重

利用层次分析法，建立层次结构后，通过上下层元素两两比较构造判断矩阵。分析步骤如下：

(1)构造两两比较矩阵，即三标度的判断矩阵为

(12)

其中：

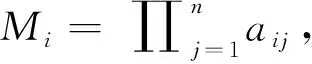
本文由于采用三标度法，其计算结果满足一致性检验。

3.3 组合权重的确定

综合上面的计算结果，得到管材选型中各影响因子的组合权重为

k=μω+(1-μ)z。

(13)

式中：k为组合权重；ω为客观权重；z为主观权重；μ和1-μ分别为变异系数法和层次分析法所得权重各占的比例，也即客、主观权重比例系数，且μ∈[0，1]。

3.4 欧氏贴近度判断

欧式贴近度是表示各方案与最优方案之间的接近程度。采用M(＊，+)算法，即进行先乘后加运算，计算欧式贴近度ρHj[21]，以此来构建复合模糊物元欧式贴近度RρH，表示为

(14)

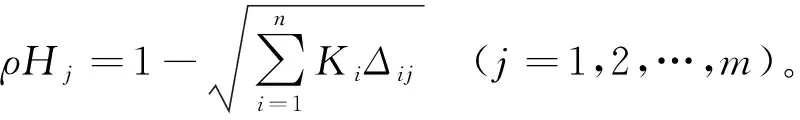
3.5 价值工程原理

价值工程是通过对选定研究对象的功能及费用进行分析，提高研究对象的价值[22]。用公式表示为

V=F/C。

(15)

式中：V为研究对象的价值系数；F为研究对象的功能系数；C为研究对象的成本系数。

4 应用实例

4.1 工程概况

新疆某引水管线工程年供水量为4 183万m3。输水管道供水对象的重要性为中等，工程规模为中型，其中输水管道总长113.01 km，采用单管输水，管径为1 600 mm，工作压力为0.6～1.6 MPa。工程主要为堆积地形，浅侵蚀地形。管线干管总长101.79 km，其中49.8 km穿越基岩，51.99 km穿越碎石土。输水管线由老至新穿越的地层岩性为碎石土。输水管线沿线的土对混凝土结构中的钢筋具微-中等腐蚀性。管道线路中有小部分路段存在冻胀性土。

本文以新疆某引水管线工程的管材类型选择为例，采用基于组合权重的模糊物元模型计算欧式贴进度进行管材优选。

4.2 管材类型

目前国内常用于输调水工程的管材主要有7种：钢管M1(SP)、预应力钢筒混凝土管M2(PCCP)、聚乙烯管(PE)、玻璃纤维增强塑料夹砂管M3(FRPM)、球墨铸铁管M4(DIP)、钢筋缠绕钢筒混凝土压力管M5(BCCP)、高性能硬聚氯乙烯管M6(PVC-UH)等。

4.3 管材选型评价指标

对于输调水工程管材选型问题，管材的选择不仅由管材本身的技术特性决定，具体工程实地的工程条件、施工方式、周边环境也是重要影响因素[23]。建立管材选择评价指标体系是管材优选中最为重要的环节。在建立指标体系中，选取评价指标应符合工程实际，划分和设置体系层次要适当[24]。影响因素大致可分为管材特性、经济性能、施工工艺和运行安全4个方面。因此，本文建立的管材选择评价指标体系如图1所示，根据新疆水利水电规划设计管理局提供的大量实地工程资料和文献调研[1-3，20-26]整理出管材选择的评价指标特性，如表1所示。

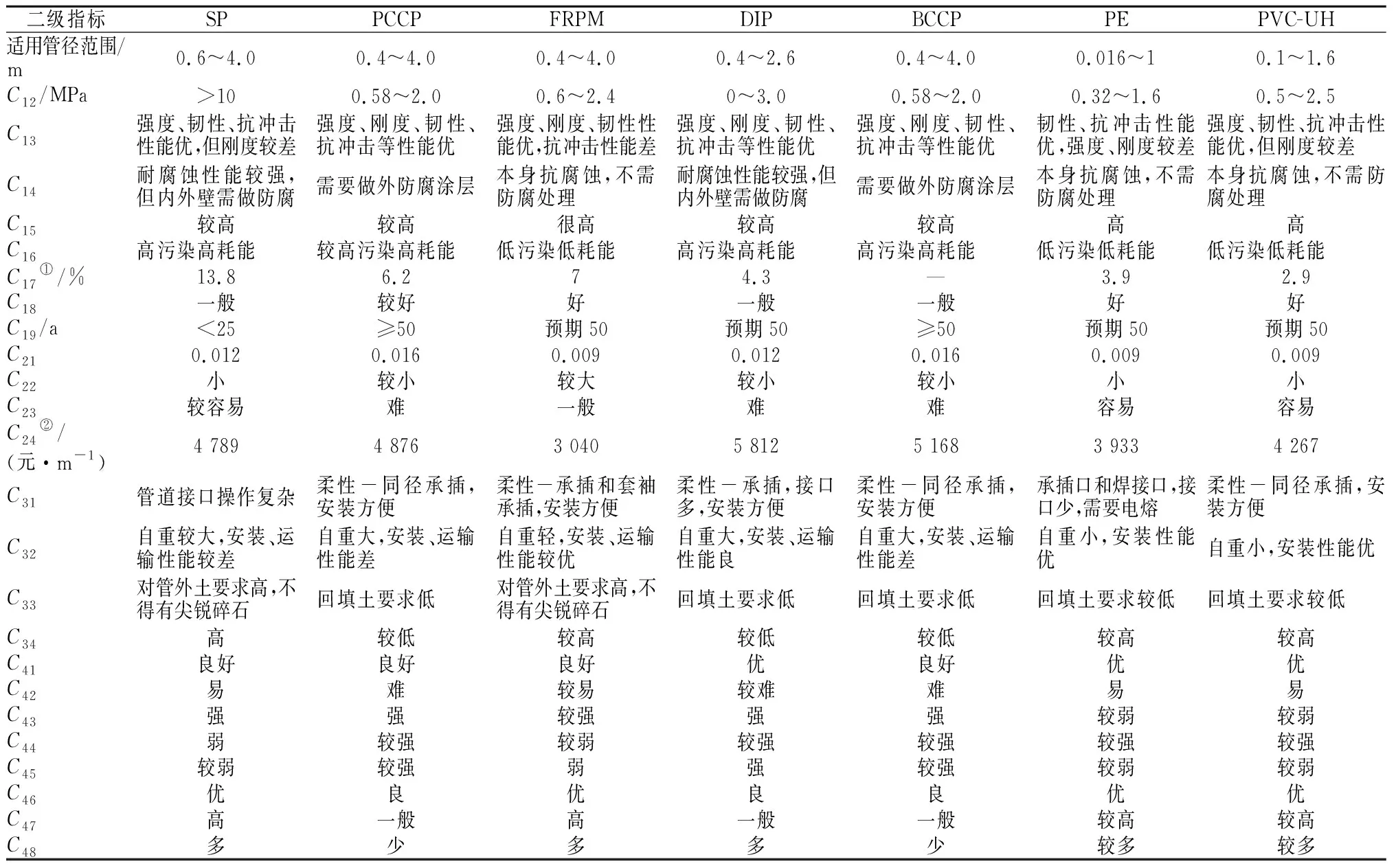
表1 输调水管道的各种评价指标特性Table 1 Characteristics of evaluation indexes for water transmission and transfer pipeline

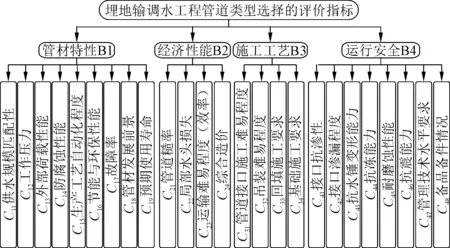
图1 长距离输水工程管材选择的评价指标层次模型Fig.1 Hierarchical model of evaluation indexes for pipe selection of long-distance water conveyance project

4.4 建立管材选型模型

利用Visual Basic编程语言[27-28]，进行了基于对象的程序编写及可视化设计，并且已经取得了软件著作权(登记号：2021SR0102228)，以新疆某引水管线工程为例进行模型验证，具体编程计算原理见4.4.1节—4.4.6节。

4.4.1 构建复合模糊物元

新疆某引水管线工程属于大流量、高压、大口径、腐蚀性环境工况，PE管道因其管径与工作压力不满足设计要求，故不参与评价。利用5级标度法进行评价指标的量化，确定每项指标的从优隶属度，表2列出了管材选择方法的各评价指标的从优隶属度评语集合数据。

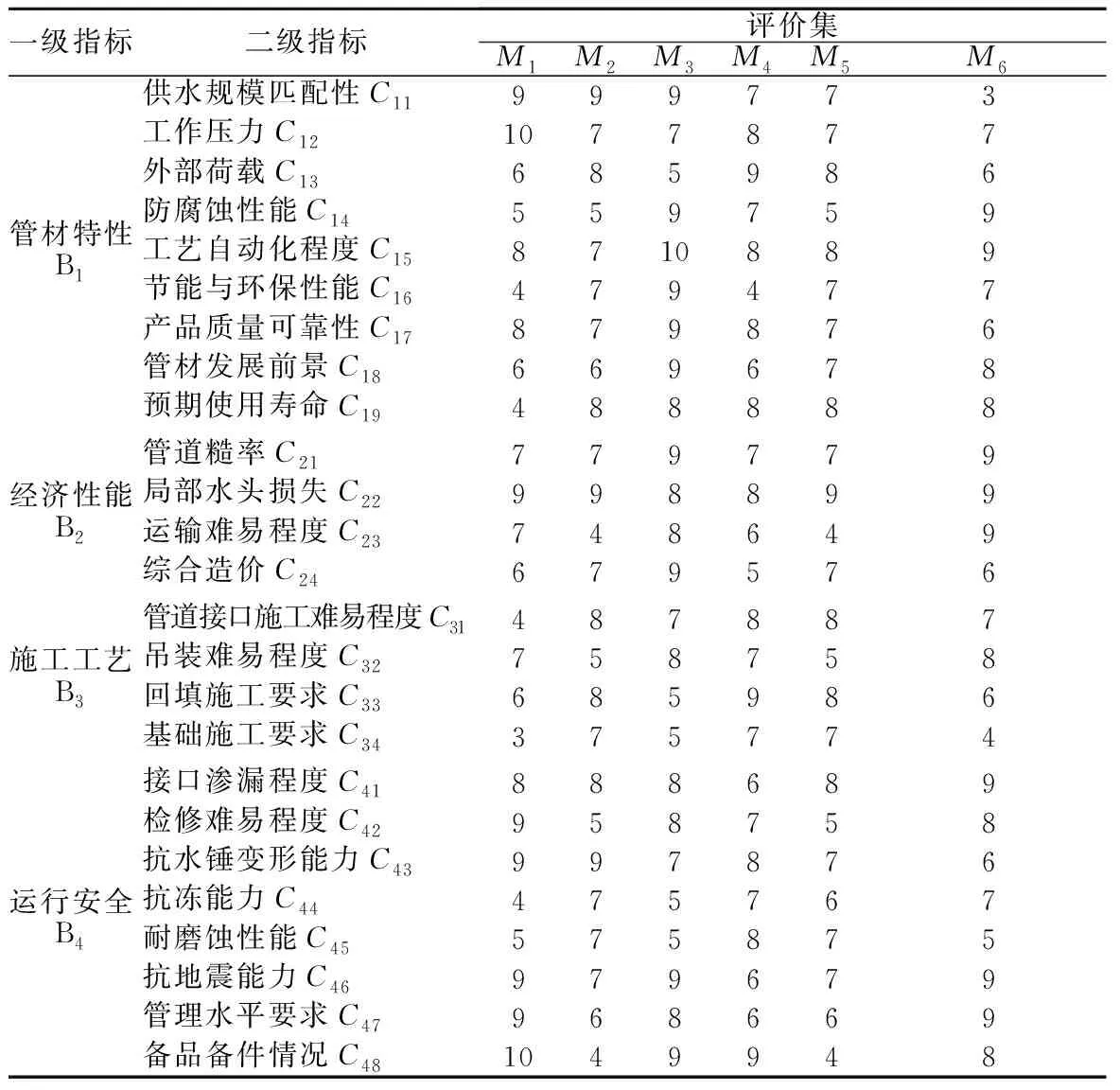
表2 管材选择各评价指标评价集Table 2 Evaluation sets of evaluation indexes for pipe selection

4.4.2 构建复合模糊物元Rmn

依据式(2)构建从优隶属度模糊物元Rmn，即

4.4.3 构建差平方模糊物元RΔ

依据式(3)—式(5)计算从优隶属度模糊物元，计算各方案评价指标与标准方案指标之间差的平方值，构建差平方模糊物元，即

4.4.4 确定评价指标组合权重

(1)采用式(7)—式(10)计算各评价指标变异系数权重ω，得

ω=[0.049 8 0.025 8 0.042 4 0.046 1

0.019 4 0.048 7 0.021 9 0.030 8 0.034 8

0.021 1 0.009 3 0.051 0 0.032 3 0.034 6

0.033 1 0.035 5 0.068 4 0.020 9 0.038 2

0.025 8 0.038 0 0.111 6 0.054 3 0.047 5

0.058 8]。

(2)利用层次分析法计算权重(见表3)，得

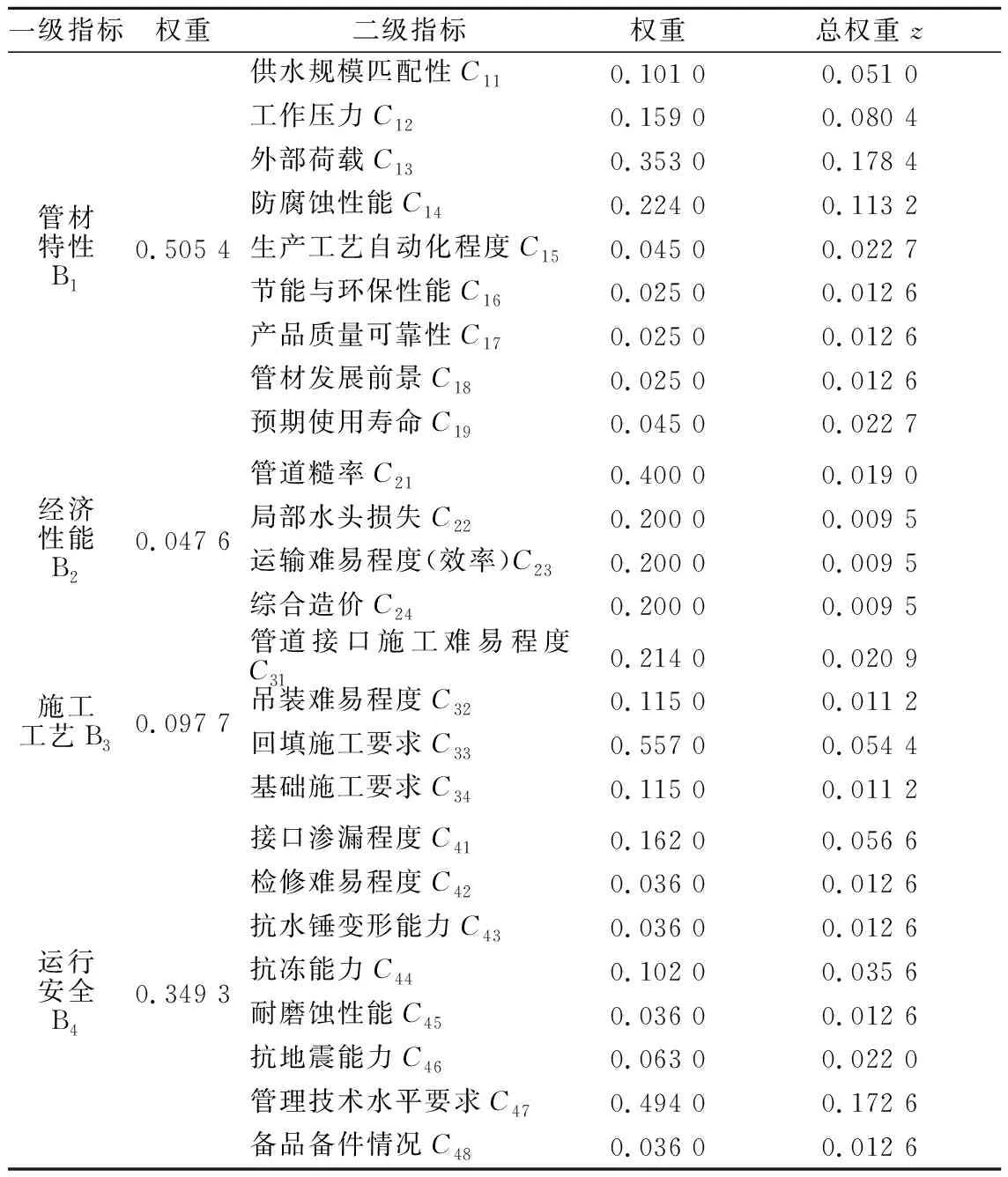
表3 AHP法计算权重Table 3 Weights calculated by AHP

z=[0.051 0.080 4 0.178 4 0.113 2 0.022 7

0.0126 0.012 6 0.012 6 0.022 7 0.019 0.009 5

0.009 5 0.009 5 0.020 9 0.011 2 0.054 4

0.011 2 0.056 6 0.012 6 0.012 6 0.035 6

0.012 6 0.022 0.172 6 0.012 6]。

(3)最后根据式(13)计算得到组合权重k，考虑到实际情况以及工程评价经验等，取μ=0.6得

k=[0.050 3 0.047 6 0.096 8 0.072 9 0.020 7

0.034 3 0.018 2 0.023 5 0.03 0.020 2 0.009 4

0.034 4 0.023 2 0.029 1 0.024 4 0.043 1

0.045 5 0.035 2 0.028 0.020 5 0.037 1

0.072 0.041 4 0.097 5 0.040 3]。

4.4.5 计算欧式贴近度

根据式(14)计算欧式贴近度RρH，得

RρH=

由基于组合权重的模糊物元模型利用欧式贴近度计算结果可以得出，管材类型欧式贴近度排序为FRPM>DIP>PVC-UH>SP>PCCP>BCCP。

4.4.6 计算价值系数

以欧式贴近度作为功能系数计算价值系数，以6种管材的预算价格(1.0 MPa，DN1600)计算成本系数，如表4所示，得到管材的价值系数排序为FRPM>PVC>SP>PCCP>BCCP>DIP。

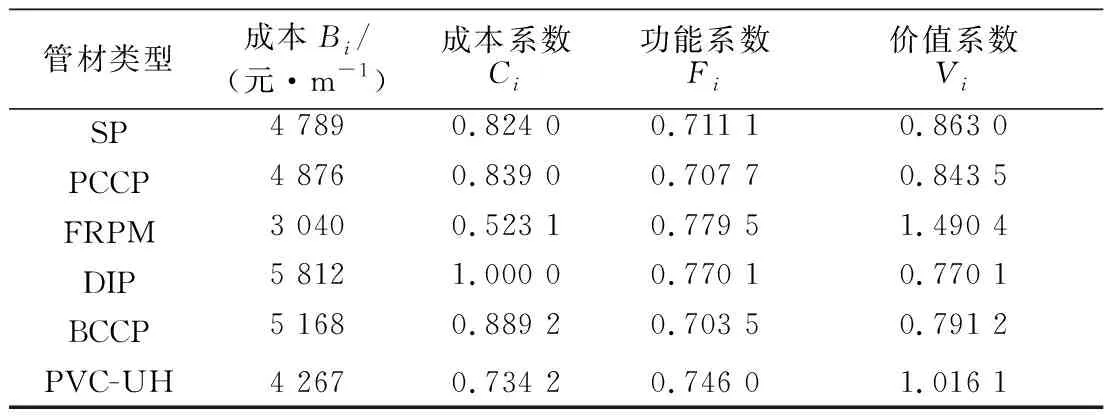
表4 管材价值系数计算Table 4 Calculation of pipe value coefficient

新疆某引水管线工程输水管材欧式贴近度评价结果中，玻璃纤维增强塑料夹砂管(FRPM)表现最优，球墨铸铁管(DIP)得分仅次于玻璃纤维增强塑料夹砂管，排名第二。DIP物理性质良好，安全可靠，在输水工程中应用广泛，但是造价高，故综合价值系数较低。根据价值工程计算得到价值系数排序，本工程玻璃钢夹砂管在欧式贴近度和价值系数均排名第一。因此，本工程选用的管材为玻璃纤维增强塑料夹砂管。

5 结 论

(1)传统方法确定指标权重时主观因素影响较大，采用改进的组合权重，引入变异系数法修正层次分析法确定指标权重时的主观性，利用各个指标权重计算得到一组较为客观的评价结果。

(2)构建了较为完善的管材选型的综合评价指标体系，将模糊物元理论应用到管材类型优选中，建立了模糊物元评价模型。工程实例表明，该模型考虑指标因素比较全面，评价结果较为客观准确，对工程管材的选型进行了有益的探索性工作。

(3)基于研究的模糊物元模型，编写了管材选型软件，使方法实际操作性、通用性更强，可以根据实地工程条件，选择出适宜本工程的最优管型，有效解决了难以定量计算的管材优选问题。

(4)随着大数据时代的到来，人工智能方法、智能监测技术迅速发展。通过收集大量实测数据集，可将利用机器学习分类预测选择的方法应用到解决管材选型问题中来。