高温损伤后岩石动态损伤本构模型

朱要亮，俞 缙，付晓强，3，任崇鸿，姚 玮，刘雪莹

(1.福建江夏学院 工程学院，福州 350018； 2.华侨大学 福建省隧道与城市地下空间工程技术研究中心，福建 厦门 361021； 3.三明学院 建筑工程学院，福建 三明 365004)

1 研究背景

深部岩石赋存环境异常复杂，常处于“三高一扰动”状态，研究复杂工况下岩石的力学性能对深部岩石工程的安全具有重要意义。核废料处置、地热能开发以及隧道火灾后重建等均涉及高温岩石问题。高温环境下，岩石矿物成分及其内部结构将发生变化，从而导致力学性质改变[1]。赵亚永等[2]采用偏光显微镜观察到岩石内裂隙发育具有各向同性特点。Yang等[3]发现温度会影响岩石的裂纹扩展。何涛和曹雅娴[4]研究表明岩石渗透率随着温度升高呈指数增长。Yin等[5]研究表明花岗岩热裂纹的数量和尺寸随温度升高而增加。Liu和Xu[6]探讨了高温后花岗岩和砂岩物理力学性质的变化规律。Chen等[7]得出了花岗岩高温后的单轴强度、弹性模量和断裂韧性随温度升高而降低的特征，并从微观结构和矿物角度解释了花岗岩的力学特性。蔡燕燕等[8]研究应力路径对高温后花岗岩的力学性能影响。此外，王春萍等[9]、闵明等[10]研究了高温花岗岩的蠕变力学性能以及劈裂试验的声发射特征，丰富了高温岩石研究成果。深部岩石不仅受到温度作用，同时还面临着动态冲击荷载[11-14]。支乐鹏等[15]研究表明高温后花岗岩动态强度与温度呈反比关系。尹土兵等[16-17]发现高温后砂岩和粉砂岩的动弹性模量和峰值强度随着温度升高而降低。刘石等[18]得出高温下花岗岩峰值应力与应变仍存在应变率效应的结论。朱要亮等[19]讨论了不同冷却方式对高温后花岗岩动态力学性能影响，发现动应力应变曲线中压密段与温度相关。李明等[20]重点讨论了高温后岩石的应变率效应，同时发现岩石压密段十分显著。Liu和Xu[21-22]也同样发现高温后花岗岩动态应力应变曲线中存在显著压密段。由此可见，温度引起的岩石裂隙损伤对动应力应变曲线具有重要影响，必须加以重视。

上述研究均从试验角度研究与分析温度对岩石动力学性能的影响，对全面了解和掌握高温后岩石动力学性能是不够的。动力本构方程是岩石动力学理论的重要组成部分，对岩石工程的设计和施工安全具有重要意义。为此，前人在动力本构模型方面开展了相关研究。单仁亮等[23]提出了统计损伤时效模型；杨明辉等[24]基于统计理论并结合元件组合方式建立动态本构方程；刘永胜等[25]通过利用岩石所处溶液pH值来定义损伤并建立了本构模型；Zhai等[26]将本构模型参数视为随机变量，采用随机反演方法建立动态本构模型，提高了峰值应力计算精度。然而上述本构方程均未考虑温度的影响。为此，许金余等[27]将模型参数视作温度的函数，建立了高温动态统计损伤模型，然而该模型需要先根据边界条件求出模型参数，再反推参数与温度之间的关系。Wang等[28]建立的温度与动力耦合作用下动态本构模型，需通过拟合确定模型参数，拟合工作量大。由前文可知，高温引起的热应力将造成热损伤，岩石孔隙较为发育，引起压密段应力应变曲线呈上凹状，该阶段弹性参数在荷载作用下逐渐增强。但鲜有模型能考虑这一因素，理论结果与实际相差较大。为此，本文首先通过核磁共振测试，得到温度对岩石孔隙发育的影响规律。然后，引入裂隙体，将其与损伤体串联起来，构建了计算岩石高温后整个过程的动态本构方法。最后，通过与试验结果的对比，验证了本构方程的合理性。

2 高温后损伤岩石动态本构模型

2.1 裂隙体本构方程

天然岩石在外界荷载作用下发生破裂，矿物分布的不均匀性导致裂隙面并非为光滑曲面，且在外荷载卸除后，已经形成的裂隙面并不能完全闭合[29]。同时天然岩石在形成的过程中，也会因各种原因导致岩石内部存在原生空隙而并非完全密实，这也是大量岩石压缩试验应力应变曲线会在前期出现上凹现象的原因所在。对于这种含有不规则裂隙的岩石，Bandis等[30]和 Barton等[31]提出非充填粗糙结构面的法向应力σn与法向变形δn的关系，即

(1)

由于

(2)

将式(2)代入式(1)可得

(3)

式中：ε为总应变；H为试样高度；a、b分别为与结构面几何特征、岩石力学性质有关的参数。

2.2 损伤体本构方程

因岩石中原生微裂纹、微孔等缺陷随机分布，前人在构建岩石统计损伤模型时，多认为岩石微元强度服从Weibull分布[24，27]。为此，在本文中同样认为岩石微元强度服从Weibull分布，其概率密度函数ψ(F)为

(4)

式中：F为微元强度；m、F0为模型参数。

根据前人研究可知，微元强度F可以直接用应变代替[27]，即

(5)

岩石材料的损伤是由局部微元体的不断破坏产生的，假设在某一级荷载作用下已破坏的微元体数目为n(ε)，损伤变量D定义为岩石中已经破坏的微元数目n(ε)与总微元数目N的比值，当加载使岩石材料达到某一应变ε时，其累计破坏微元数目为

(6)

因而岩石损伤演化方程与单轴条件下应力-应变本构关系可分别表示为：

(7)

σ=E0ε(1-D) 。

(8)

式中E0为常温下岩石弹性模量。

温度对岩石的劣化作用主要表现在两个方面，一是由于温度升高产生的热应力作用于岩石内部结构，引起矿物颗粒的膨胀诱导微观弱面的形成，且进一步产生局部的滑移和摩擦诱导微孔裂隙的增大[32]。温度引起的孔隙率变化可由核磁共振试验来确定；二是温度升高改变了岩石内部晶体或颗粒的排列结构，宏观上表现为力学性能的减弱，弹性模量有所下降。为此，可利用常温下和高温作用后的岩石弹性模量比值来定义温度损伤[5，28]，即

(9)

同时考虑温度损伤的本构方程为

σT=E0ε(1-D)(1-DT) 。

(10)

式中：σT、ET分别为高温作用后的岩石应力与弹性模量；DT为温度引起的损伤。

2.3 全过程动态本构方程

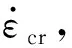
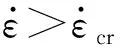
为更好地描述岩石受力全过程，本文提出的本构模型如图1所示，即黏性体与损伤体并联，随后串联一个裂隙体，并通过一个开关来定义各个元件参与工作的先后顺序。当外荷载引起的应力未超过裂隙闭合应力时，其本构方程由公式(3)确定，而当应力超过闭合应力时，根据元件串联与并联的基本规则，可得本构方程为

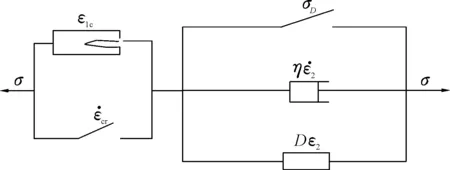
图1 考虑裂隙与损伤的动态本构模型Fig.1 Dynamic constitutive model in consideration of fracture and damage

(11)

所以全过程本构方程为：

(12)

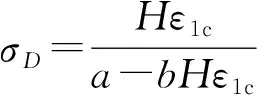
2.4 损伤体本构模型参数确定

对于损伤体部分，本构模型参数中的m、F0可以通过全过程应力应变曲线上的峰值应力点的值来确定，即在峰值点(σc，εc)处满足边界条件：

(13)

由此可得

(14)

(15)

联立上面两式可以得到：

(16)

式中：σc、εc分别为峰值点处应力和应变；ε2c=εc-ε1c为峰值点处黏性体(损伤体)应变。

3 高温后岩石动态冲击试验

3.1 试验方案

为保证岩样一致性，从一完整花岗岩大样相邻部位钻取岩样，并切割、打磨加工成直径 50 mm、厚度25 mm 的圆柱体，随后通过测重和纵波波速测试等手段进行挑选试样。试验设定4组温度，为25(常温)、200、400、 600 ℃。最终选取的试样平均质量为512.2 g，平均纵波波速为3 966 m/s，试样均匀性较好。随后按如下步骤进行试验：

(1)将试样放入箱式电阻炉内以10 ℃/min的速度加热至预定温度并恒温2 h确保岩样均匀受热后取出自然冷却，冷却后岩样见图2。

图2 不同温度处理后的花岗岩Fig.2 Granite specimens treated with different temperatures

(2)将冷却后岩样进行真空饱和处理，待完全饱和后利用MesoMR23-060H-I型核磁共振成像分析仪开展核磁测试。

(3)为避免水分对冲击试验结果造成影响，对核磁测试后的岩样进行烘干处理，随后进行应变率为50 s-1的动力冲击试验。为获得可靠的应力应变关系，在入射杆端部黏贴紫铜波形整形器，并在试样与杆件接触部位涂抹凡士林以减小摩擦。

从图2可以看到，当温度为200 ℃和400 ℃时，岩石外观与常温相比并未呈现明显变化，随着温度升高至600 ℃，岩石表面开始呈现淡红色的特征且出现肉眼可见细微裂隙，具体原因见3.2节中分析。

3.2 核磁试验结果

核磁共振检测技术是利用水的原子核被极化产生的横向磁化矢量衰减时间(即弛豫时间)与饱和岩样孔隙体积存在的对应关系，通过对谱面积进行标准刻度转换，从而计算出岩石的孔隙度和孔径分布。对岩样内部孔隙数量与孔径分布进行量化分析，根据测试结果绘制成像信息图，能更直观地展示岩石内部裂隙情况。图3为不同温度处理后花岗岩的核磁扫描伪彩图和核磁共振T2谱面积变化图，伪彩图中红色表示孔隙。

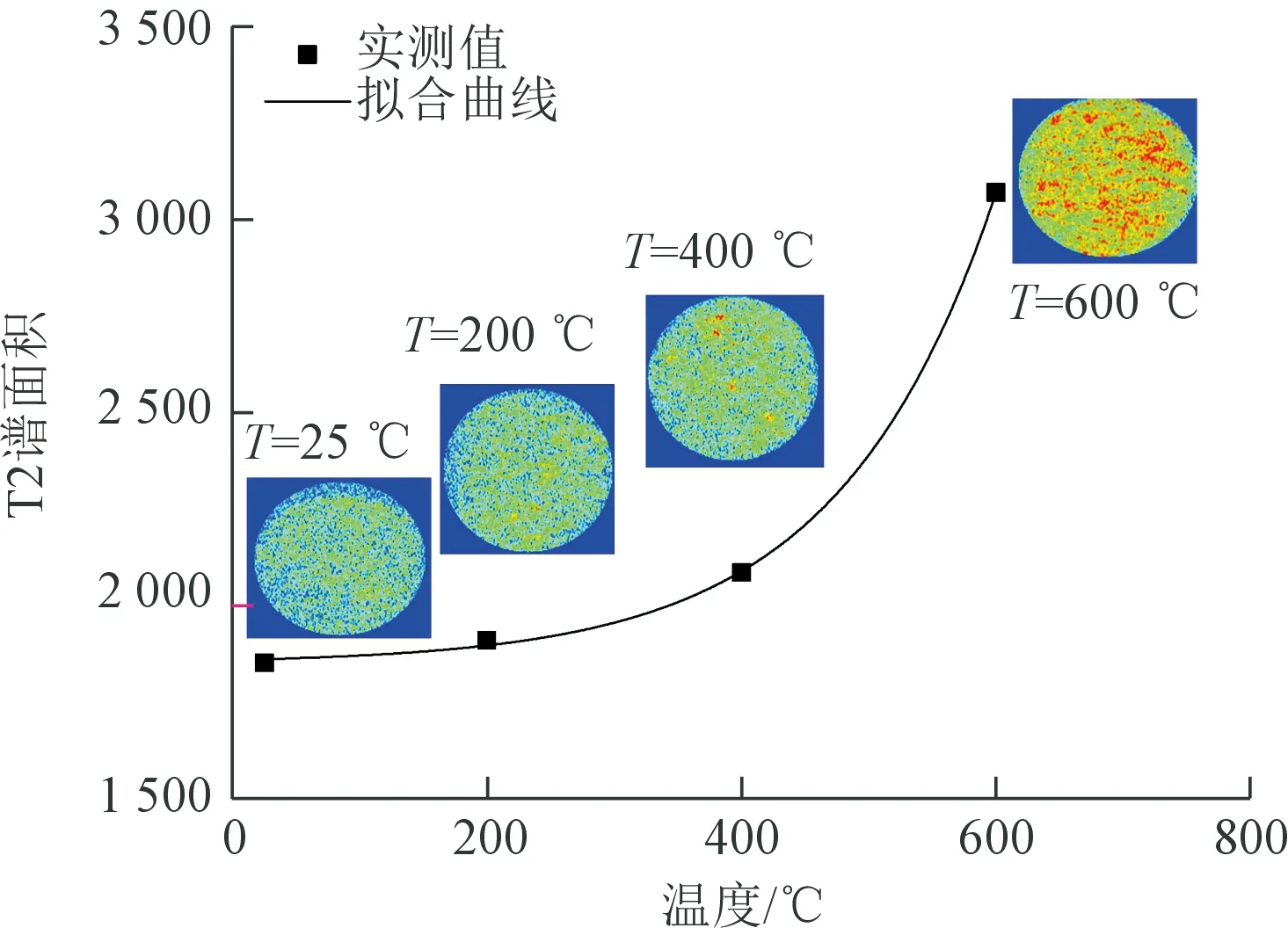
图3 核磁共振T2谱面积Fig.3 T2 spectrum area of NMR

从图3中可直观看到当温度在25～400 ℃时，岩样内部产生部分裂隙，但总体变化并不明显，而当温度升高到600 ℃时，花岗岩内部产生了大量裂隙。分析其原因是花岗岩内部含有石英、长石、云母等多种矿物，不同矿物本身热膨胀系数不同，经过高温作用后，矿物间不均匀热膨胀引起晶粒面滑移，产生微裂隙，因而伪彩图中出现部分红点。由于矿物受温度影响存在一个阈值，即当温度低于该值时，温度影响并不显著，研究表明花岗岩内主要石英在573 ℃会发生相变[7，16]，引起体积膨胀，所以600 ℃高温处理后的花岗岩内部产生了十分显著的裂隙，在伪彩图中则显示为大量的红色区域。同时，从图3可以看到T2 谱面积随着温度升高而呈现非线性增加趋势，对其采用指数拟合结果见式(17)，拟合相关性系数高达0.99。

λ(T)=9.22exp(T/122.8)+1 850 。

(17)

式中：λ(T)为不同温度处理后T2谱面积；T为温度(℃)。

进一步对岩样内部裂隙进行分析，计算其核磁共振孔径分布，结果如图4所示。

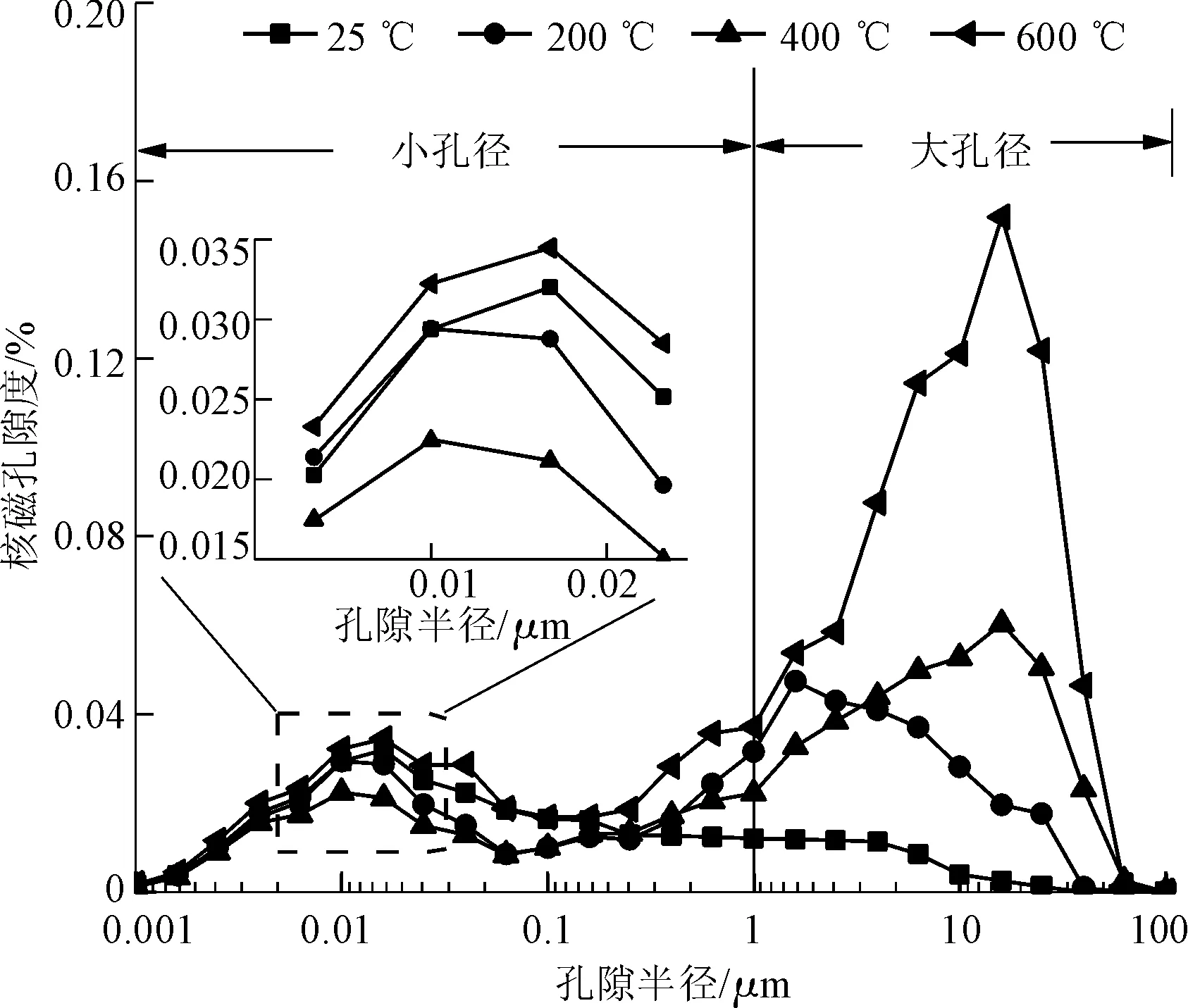
图4 横截面核磁孔隙度分布Fig.4 Pore size distribution of cross-sectional area

在图4中以1μm为分界点[33]，将孔径分为大孔径和小孔径2种类型。从图4可以看到，当温度为25 ℃时，T2谱曲线仅有一谱峰且分布在小孔径区域，这表明原始岩样中以小孔径孔隙为主，试样较为密实。而经过不同温度处理后，T2谱曲线在大孔径和小孔径区域均出现1个谱峰。仔细观察可以发现，在小孔径区域小孔隙数量随温度升高先减少后增加，当温度达到600 ℃时，小孔径数量超过原始岩样。而在大孔径区域孔径大小和大孔隙数量均随温度升高而增加。这是因为当温度未超过矿物相变阈值时，温度对岩石的主要影响是使其所含矿物体积发生膨胀，从而使试样内原生微孔隙闭合，导致小孔隙减少。与此同时，不同矿物之间不均匀膨胀引起的温度应力使得矿物挤压破碎或脱离从而形成大孔径孔隙，温度越高这种现象越明显，即图4中表现出的大孔径尺寸和数量随着温度升高而显著增加。

3.3 动力冲击试验结果

不同温度处理后花岗岩动力冲击应力应变结果如图5所示。考虑到岩石应力应变曲线上存在压密段，因而本文采用40%和60%峰值应力对应数据计算弹性模量[18，22]，其公式为

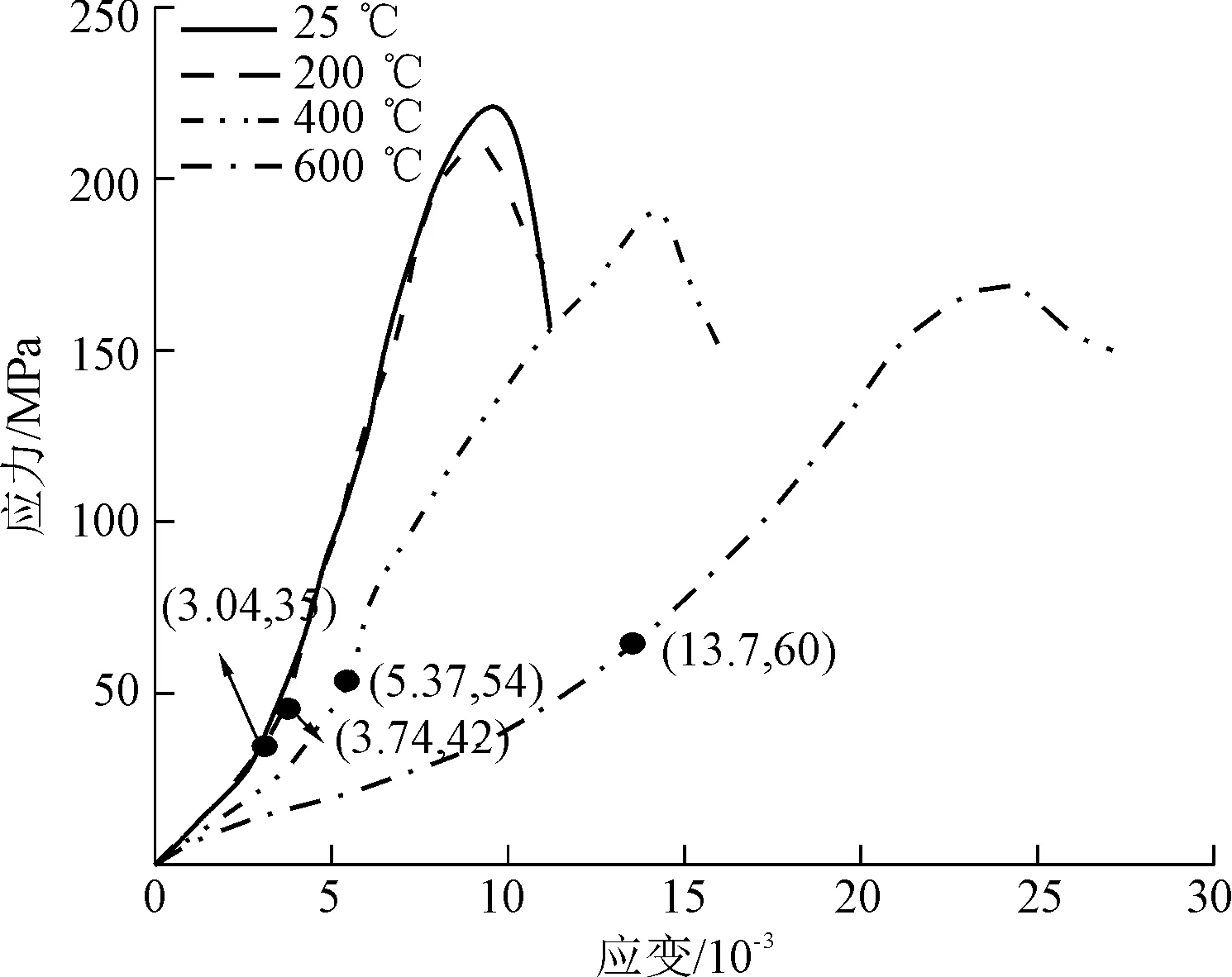
图5 高温后花岗岩动力试验结果Fig.5 Dynamic test results of granite after high temperature

(18)

式中：σ40、σ60分别为对应0.4σc和0.6σc处的应力；ε40、ε60则为对应的应变。

从图5中看到随着温度升高，花岗岩动态峰值强度降低且应力应变曲线前期上凹现象越来越明显，表明温度作用引起岩石内部产生裂隙，图中括号内数字为从应力应变曲线确定压密段对应的闭合应变与闭合应力。弹性模量计算结果得到4种温度下对应的弹性模量分别为29、34、16、11 GPa。根据计算结果可知200 ℃后花岗岩弹性模量相较于常温状态下的弹性模量小幅增加，随后其值随着温度升高而快速下降，当温度达到600 ℃时，花岗岩弹性模量降低到11 GPa，仅为常温下弹性模量的38%。

4 动态本构模型验证

4.1 裂隙体模型参数

从前文分析可知，考虑裂隙损伤的动态本构模型由两部分组成，对于第一部分裂隙损伤模型参数的值，可根据常温时应力应变曲线拟合确定。应力应变曲线前期上凹越明显则表明岩石内部裂隙越多，试验结果发现温度越高，核磁T2谱面积越大，这表明裂隙体模型参数与核磁试验结果存在相关性。因此，基于核磁孔隙度试验结果我们可以假设其他温度下模型参数与常温下模型参数之间存在如下关系：

(19)

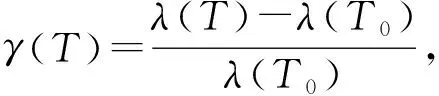
通过对常温时裂隙体试验数据拟合得到a和b，随后取温度影响调整系数k=2则可得其他温度下的参数值，计算结果见表1。

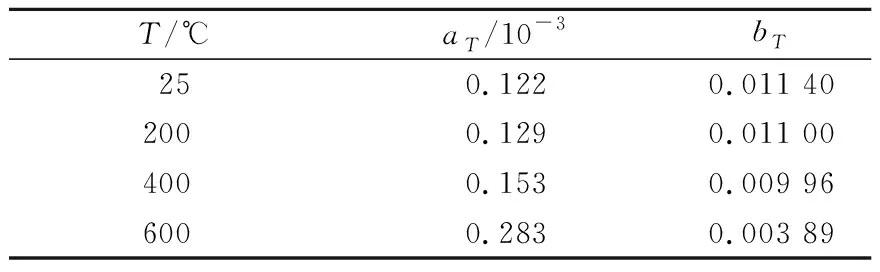
表1 裂隙体模型参数Table 1 Parameter values of the fracture body

4.2 损伤体模型参数

对于本构模型中的黏性系数取值，根据文献[28]可以知道花岗岩黏性系数均值取值区间为0.15～0.21 MPa·s，整体变化幅度不大，因而在本文中取其均值0.18 MPa·s。根据试验结果获得峰值应力应变和峰前上凹段对应的应力应变(即闭合应力、闭合应变)，具体见图5。利用公式(16)确定损伤体模型参数，结果如表2所示。

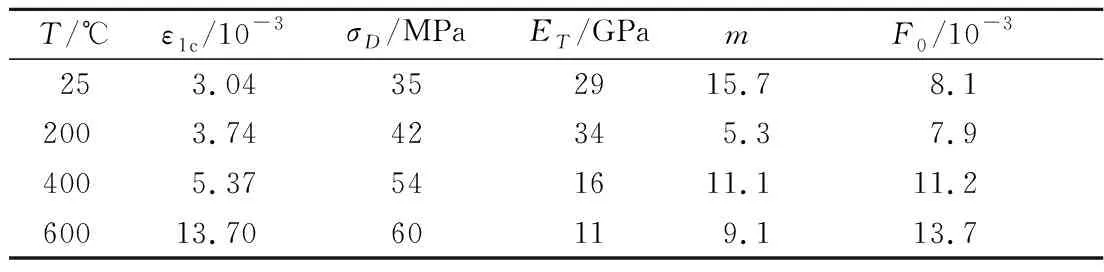
表2 本构模型参数Table 2 Parameter values of the constitutive model

根据表2中计算结果，将各参数值代入本构模型中，得到应力应变理论值，并与试验值对比，结果如图6所示。理论值与实测值的相关系数从25 ℃到600 ℃分别为0.987、0.997、0.996和0.993。由此可见，本文模型与试验结果高度吻合。

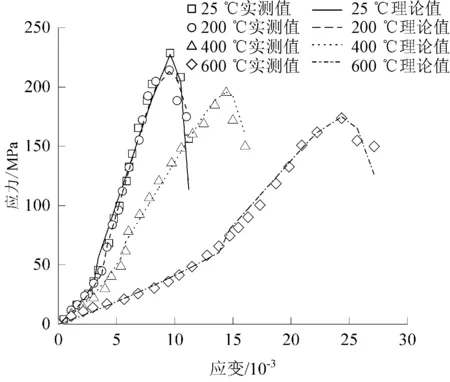
图6 高温后花岗岩动态应力应变实测值和理论值比较Fig.6 Comparison of dynamic stress-strain between test values and theoretical values of granite after high temperature

为进一步验证本文提出本构模型的适用性，对文献[27]的高温岩石动力试验数据进行计算，并与许金余等提出的本构模型对比。因文献[27]没有开展核磁或其他微观测试，孔隙发育与温度的关系无法确定，故不同温度下的裂隙体参数均采用拟合确定。不同温度下的闭合应变与闭合应力均根据应力应变曲线上凹情况确定。经计算后得到应力应变理论值，并与试验结果对比，具体如图7所示。

图7 本构模型验证Fig.7 Verification of the constitutive model

从图7中可以看到，本文建立的动态本构模型在压密段具有明显的上凹形状，能够体现温度损伤对岩石动态应力应变的影响。与文献[27]所建立的岩石动态本构方程相比，本文所建模型能够更好地模拟全过程动态应力应变关系，且只需对常温时上凹段数据拟合，其他温度下的裂隙体模型参数由核磁测试结果进行转换求解即可，从而将岩石应力应变与微观特征建立联系。为了进一步说明本模型的优越性，计算100～400 ℃高温后岩石2种方法理论值与实测值的相关系数分别为：0.996(0.998)、0.998(0.991)、0.997(0.995)，其中括号内为文献[27]相关系数。虽然在100 ℃时本文模型结果相关性略低于文献[27]，但也高达0.996，文献[27]则是因为其计算值沿着实测值上下波动，从而提高了其相关性。但从绝对误差来看，在压密段，本文模型绝对误差最大值分别为2.3、1.0、2.4 MPa，而文献[27]对应绝对误差最大值则为：10.3、25.8、12.2 MPa。由此可见，本文模型对高温后岩石全过程动态模拟比本构模型更为准确。此外，文献[27]在确定模型参数与温度的关系时，需要利用7个参数进行拟合，而本文提出的模型在上凹段仅需2个参数，且损伤体模型参数可根据峰值点处满足的边界条件来确定，计算方法简单且物理意义明确。

5 讨 论

以T=200 ℃为例，在模型验证的基础上，对模型参数进行分析，探讨各参数取值对本构模型的影响，具体如图8所示。

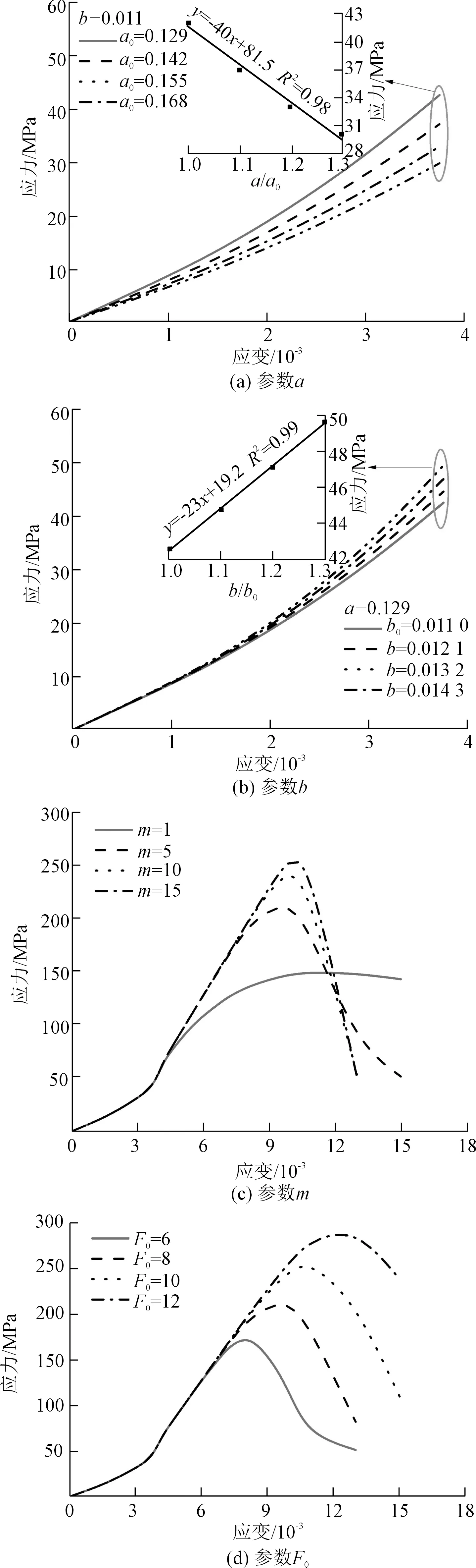
图8 各参数对模型的影响Fig.8 Effect of parameters on theoretical curve

从图8(a)和图8(b)可知裂隙体闭合应力随着参数a的减小、b的增大而增大，但相同变化幅度时，参数a引起的裂隙体应力应变曲线与初始值(a0)确定的应力应变曲线偏离程度明显大于参数b引起的结果。同时绘制闭合应力与参数比a/a0、b/b0的变化规律，可以发现二者呈线性关系，经拟合可得线性斜率绝对值分别为40和23，这表明闭合应力对参数a更为敏感。

从图8(c)和图8(d)可知，高温后花岗岩动力峰值强度随着损伤体中Weibull分布参数m的增大而增大，且峰后应力跌落愈快，这表明岩石的延性减弱，脆性增强。这与试验结果表现出来的温度越低，强度越高，峰后下降越快的特征相符；高温后花岗岩动应力应变曲线形状并不受Weibull分布参数F0的影响，该值仅控制峰值应力和峰值应变。综上所述，考虑裂隙体高温后岩石动态本构模型全过程曲线形状由裂隙体参数a和b，以及损伤体中Weibull分布参数m和F0共同确定。

6 结 论

(1)温度会对花岗岩试样内部结构产生显著影响，经核磁扫描测试可以发现常温时原始岩样内部以小孔径孔隙为主，随着温度升高，花岗岩试样内部逐渐产生大孔径孔隙，温度越高，孔径尺寸越大且占比越多。核磁扫描技术能够准确地量化温度对花岗岩内裂隙发育情况的影响。

(2)通过引入裂隙体本构模型能够很好地模拟应力应变曲线前期的压密段部分，采用T2谱面积来表征裂隙体本构模型参数的变化规律可获得其他温度下裂隙体模型参数值，经与试验数据对比，匹配性较好。

(3)本文提出的裂隙体与损伤体串联的本构模型能够较好地表征动态冲击全过程应力应变关系，模型参数易于获得且物理意义明确；峰值强度随着损伤体中Weibull分布参数m和F0的增大而增大，但m同时反映了峰后应力跌落程度，而参数F0仅控制动态峰值强度和峰值应变，对模型曲线并无影响。