膨胀土中EPS缓冲层-悬臂式挡墙支护结构的受力变形数值模拟
王协群,匡文壮,韩 仲,邹维列
(1.武汉理工大学 土木工程与建筑学院,武汉 430070; 2.武汉大学 土木建筑工程学院,武汉 430072)
1 研究背景
聚苯乙烯泡沫(Expanded Polystyrene,EPS)是聚苯乙烯颗粒经预发泡、塑模等工艺而得到的土工合成材料,具有密度小、压缩性大等特点。自1972年首次应用以来,EPS作为减载材料受到国内外工程界的青睐,被广泛应用于公路、建筑、水利、市政等工程领域。对于膨胀土地区的挡墙,当墙后膨胀土吸水膨胀时,由于受到挡墙侧向约束,将对挡墙产生显著的侧向膨胀力,可能导致作用在挡墙上的侧压力超过静止土压力[1],造成挡墙出现大变形、剪断等破坏[2]。因此,在挡墙与墙后膨胀土之间设置一定厚度的EPS板作为缓冲层,形成“膨胀土-EPS缓冲层-挡墙”体系,通过EPS缓冲层的侧向压缩变形可有效地减小作用在挡墙上的侧压力,从而增加挡墙的安全性[3-6]。
目前对EPS缓冲层应用于膨胀土悬臂式挡土墙的研究还较少。悬臂式挡墙在减小土压力上有积极作用,EPS缓冲层也能进一步减小土压力,因此探究悬臂式挡墙-EPS缓冲层-膨胀土支护体系具有实际工程意义。Ertugrul等[5]开展了在悬臂式挡墙与墙后砂石之间铺设EPS缓冲层的物理模型试验及相应的数值模拟研究,发现随着挡墙相对柔度的增加,EPS对挡墙的减压贡献降低;当作用在EPS上的应力未超过其屈服应力时,墙身高度对减载效果没有显著改变。郑俊杰等[7]提出了适用于膨胀土地区高填方路堤边坡的刚柔复合桩基挡墙结构,用FLAC3D模拟挡土墙与膨胀土之间铺设EPS板的支护减压体系。与含EPS板的刚性桩基挡墙结构对比,含EPS板的刚柔复合桩基挡墙结构的墙背土压力、抗滑桩桩身弯矩和剪力、挡土墙和抗滑桩水平位移均明显减小。
本文探讨EPS缓冲层应用于膨胀土悬臂式挡土墙,分析EPS和膨胀土的力学参数及几何尺寸等设计因素对于支护体系减压效果的影响规律,为实际工程提供参考。
2 膨胀变形在ABAQUS中的模拟方法
膨胀土在吸湿和脱湿过程中表现出显著的膨胀和收缩变形。膨胀土的湿度效应与材料的温度效应具有可比性,因为温度升降会使材料发生体积的胀缩[8]。因此,可将水分在土体中渗流形成的湿度场在ABAQUS分析软件中以土体在不同温度边界条件下通过热传导形成的温度场进行等效,材料在不同温度下的膨胀比拟膨胀土在不同含水率下的膨胀,从而实现对膨胀土增湿膨胀过程的模拟[9]。
在非饱和土中,基于Darcy定律的渗流微分方程为
式中:kx、ky、kz分别为x、y、z方向的渗透系数;h为总水头;ωm为土的质量含水率;ρw为水的密度;ρd为土的干密度;t为时间。
(2)
式中:β为膨胀土的增湿膨胀系数;δij为Kronecker记号。
在热力学中,不考虑材料本身发热的情况下,热传导的微分方程为
(3)
式中:λx、λy、λz分别为x、y、z方向的导热系数;ρ为密度;Cv为材料的比热容;T为温度;t为时间。
(4)
式中η为材料的热膨胀系数。
对比渗流微分方程导出的式(1)、式(2)与热力学理论中式(3)、式(4)可知,两者在公式结构上相同,参数之间存在对应关系,即ωm对应CvT,β对应η。因此,可用材料在温度场作用下发生的热膨胀变形模拟膨胀土在增湿过程中湿度场作用下发生的吸湿膨胀变形。
3 膨胀土膨胀特性试验研究
3.1 试验土样
基于南阳膨胀土开展膨胀特性研究。南阳膨胀土的物理性质指标见表1。根据《膨胀土地区建筑技术规范》[10],该膨胀土为中膨胀土。

表1 南阳膨胀土物理性质指标Table 1 Physical properties of Nanyang expansive soil
3.2 试验内容
对南阳膨胀土利用可测侧向膨胀力的改进的K0固结仪[11]开展侧限条件下的有荷膨胀试验和基于平衡加压法的常体积膨胀力试验。试验所用饼状试样的干密度为1 500 kg/m3,初始含水率为17%,直径为61.8 mm,高为20 mm。
有荷膨胀试验中,在K0状态下对各试样施加不同竖向荷载(0、25、50 kPa),待竖向变形稳定后,记录百分表的膨胀前初始读数,然后通过仪器底座处的注水阀门使试样增湿至饱和(饱和含水率为30%)。当试样竖向变形在6 h内≤0.01 mm时,结束试验并记录百分表的最终读数以及从K0固结仪中环相搭配的数采系统中读出膨胀后侧向土压力。
常体积膨胀力试验中,同样通过仪器底座的注水阀门使安装在K0固结仪上的试样吸水膨胀,根据百分表的变化(土体产生膨胀或者压缩)调整土体的竖向荷载,使试样高度维持20 mm不变。当百分表的读数在当前竖向荷载的作用下在6 h内变化≤0.01 mm时,可以认定此时的竖向荷载为土体的竖向膨胀力,对应的数据采集系统中的侧向土压力为土体的水平膨胀力。
3.3 试验结果分析
假定膨胀土为弹性材料,考虑膨胀土的膨胀系数在水平和竖直方向上的值不同,结合广义胡克定律,可推导K0状态下膨胀土的应力-应变方程为
(5)
式中:εh、εv分别为水平应变和竖向应变,其中εh=0;σh、σv分别为水平应力和竖向应力;υ为泊松比;E为弹性模量;βh为膨胀土的水平膨胀系数;βv为膨胀土的竖向膨胀系数。若已知土体的弹性模量和泊松比则可反推膨胀土的水平及竖向膨胀系数。
表2总结了万梁龙[12]所测饱和南阳膨胀土在不同竖向荷载下的弹性模量。根据式(5),采用表2中土体弹性模量,计算得到南阳膨胀土水平及竖向膨胀系数,如表3所示。
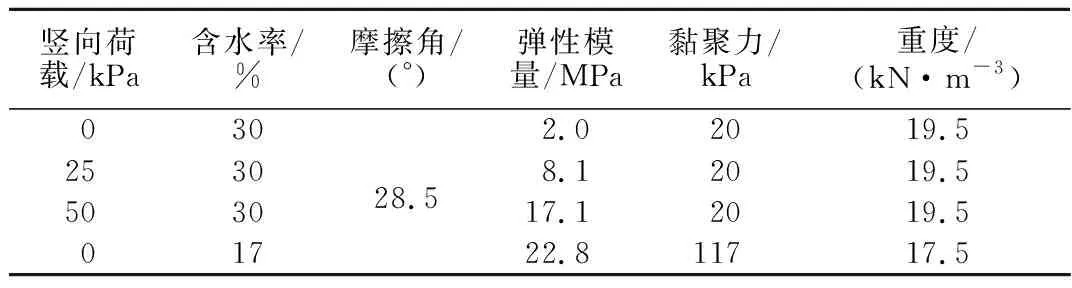
表2 南阳膨胀土相关参数Table 2 Parameters of Nanyang expansive soil
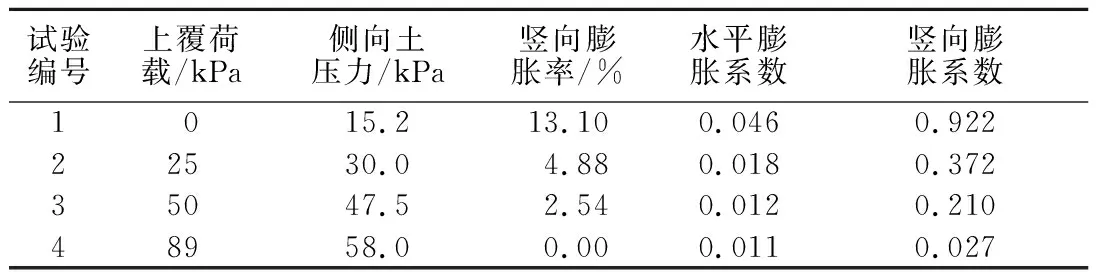
表3 膨胀试验结果Table 3 Result of expansion test
4 参数选取及验证
4.1 膨胀土膨胀特性数值模拟验证
为验证数值模拟的效果,通过ABAQUS软件建立与有荷膨胀力试验中相同的饼状试样模型。模拟的过程为先对试样施加竖向荷载及侧向位移约束,然后根据第2节模拟方法中的对应关系,即ωm对应CvT,对初始含水率为17%的南阳膨胀土增湿至饱和含水率30%,相应的在软件中设置热属性时,取比热容为0.01 J/(kg·K),对试样从初始温度17 ℃升温至30 ℃。数值模拟中采用的南阳膨胀土在不同应力和湿度条件下的力学参数见表2,其中土体的黏聚力及弹性模量随含水率的变化而线性变化;泊松比取为常数0.2[12]。
模拟值与实测值对比如图1所示。从图1可以看出模拟3种竖向荷载下的侧向土压力及竖向应变的结果与试验中测得的值较为接近,说明了本文数值模拟方法具有可靠性。
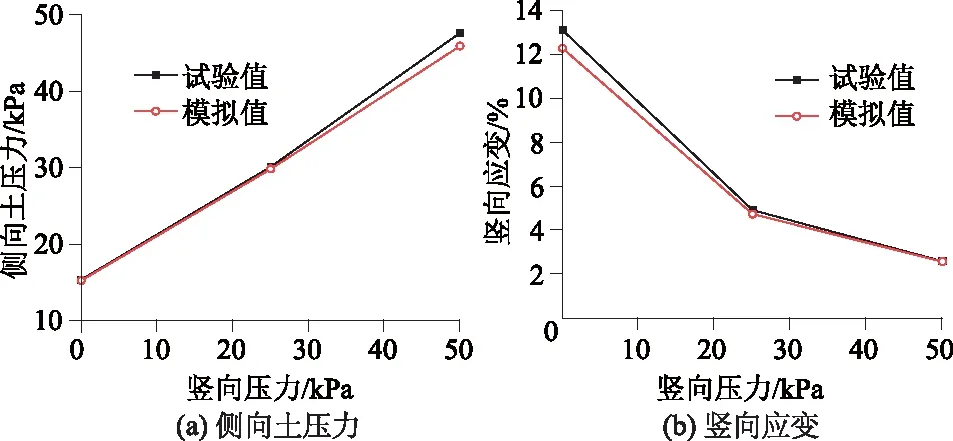
图1 试验结果与模拟结果对比Fig.1 Comparison between test and simulation results
4.2 挡土墙及EPS参数选取
4.2.1 悬臂式挡墙参数
悬臂式挡墙的柔度是影响其工作性能的基本参数,Younan等[13]提出了悬臂式挡墙相对柔度dw的概念,并指出相对柔度dw与墙体厚度tw成反比,因此本文对挡墙墙厚tw=0.20、0.25、0.30 m的3种悬臂式挡墙进行分析[14]。其中设墙体材料的弹性模量为30 GPa,泊松比为0.18。
4.2.2 EPS缓冲层参数
为探究EPS缓冲层的厚度、弹性模量对悬臂式挡墙工作性能的影响,以3种不同密度(11.9、14.9、18.5 kg/m3)和3种不同厚度(0.25、0.50、0.75 m)的EPS缓冲层建立数值模型。Horvath[15]建议用压缩刚度K来描述EPS压缩性能,即
K=Eeps/teps。
(6)
式中:Eeps为EPS的弹性模量;teps为EPS的厚度。
缓冲层参数见表4。EPS的泊松比在弹塑性阶段下的泊松比较小,所以在模拟中均设为0.01。表4中,EPS12表示的是密度为11.9 kg/m3(约为12 kg/m3)的EPS缓冲层,其余同理。
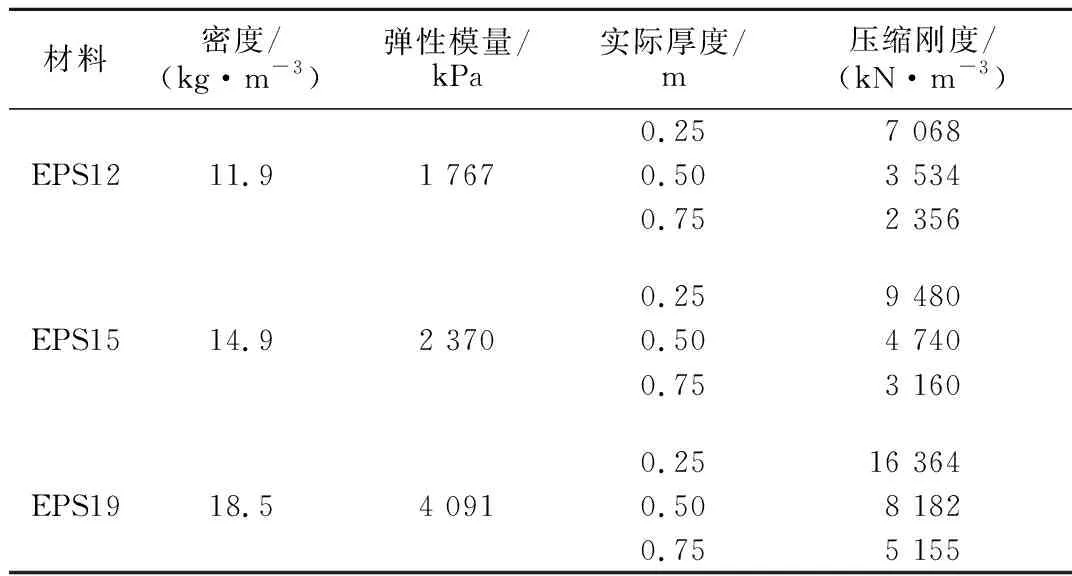
表4 EPS缓冲层相关参数Table 4 Parameters of the EPS buffer layer
EPS缓冲层的应力-应变(σ-ε)曲线分为线弹性段、塑性段、压密段3个阶段[16]。但其中EPS压
密段在本文体系中难以达到,故只对前2个阶段进行试验。而在数值软件ABAQUS中有可模拟EPS的σ-ε关系的模型,即可压碎泡沫模型[17]。以EPS15为例,先将该缓冲层用电热线切割成50 mm的立方体,再将其放在万能试验机上以10 mm/min的加载速率进行加载,得到σ-ε曲线;最后通过ABAQUS的可压碎泡沫模型对其进行拟合。图2对比了σ-ε关系的实测结果与拟合结果。从图2可知可压碎泡沫模型可以较精确地模拟EPS缓冲层的σ-ε关系。
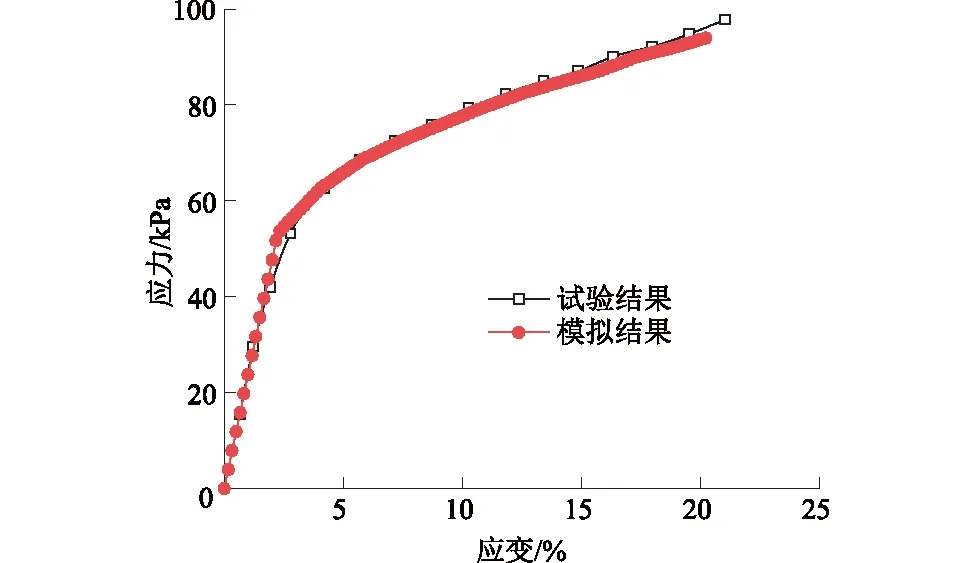
图2 EPS的σ-ε关系试验结果与模拟结果对比Fig.2 Comparison of σ-ε relation of EPS betweenlaboratory test and constitutive modelling
5 模型建立与参数分析
5.1 悬臂式挡墙-EPS缓冲层支护体系模型
建立图3所示的模型(以下简称基本模型)。用ABAQUS模拟二维平面应变条件下铺设EPS缓冲层的悬臂式挡墙。根据文献[18],河南南阳盆地地区的膨胀土大气影响深度约为3.5 m。本文取墙后填土深度为3 m以考虑大气影响深度内膨胀土胀缩对挡墙的影响。挡墙后膨胀土宽度范围(Tsoil=20 m)内无外荷载。EPS缓冲层沿墙身等厚铺设。
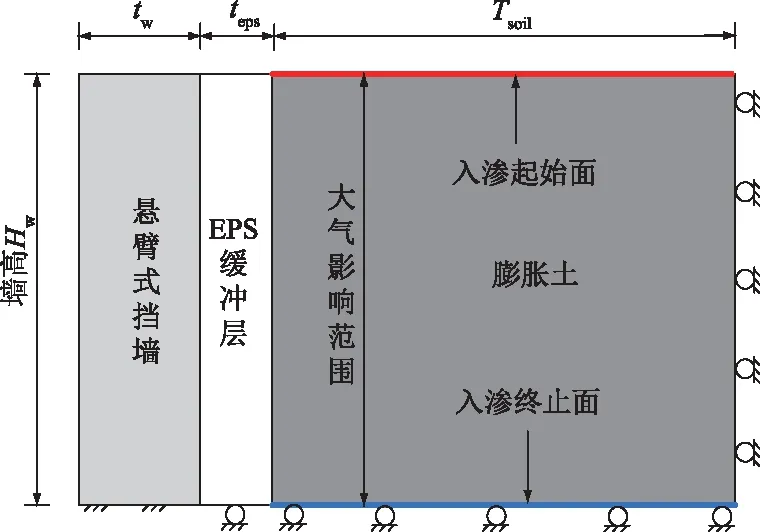
图3 数值分析模型Fig.3 Model for numerical analysis
墙体、EPS缓冲层、膨胀土均采用四边形单元模拟。墙体采用弹性模型,缓冲层采用可压碎泡沫模型,膨胀土采用摩尔-库伦弹塑性模型,并采用热-力耦合计算模式进行膨胀计算。
假设膨胀土初始含水率为17%,并且从土体顶部开始增湿,直至顶部含水率达到饱和含水率30%,因此在大气影响深度范围内,土体含水率由顶部的30%向下逐渐减小至大气影响深度处的初始含水率17%,如图4所示。对应到数值模拟的温度场中,土体表面为高温边界30 ℃,大气影响深度处为低温边界17 ℃。墙底板固定端约束,墙身无约束。膨胀土底端竖向约束,右侧水平约束。
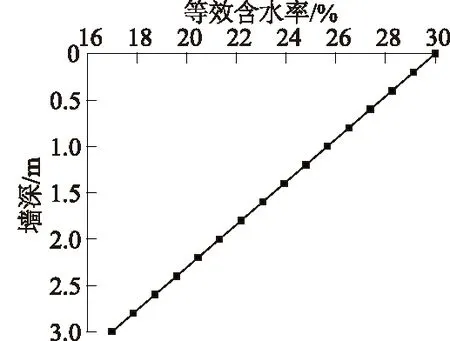
图4 模型中含水率分布Fig.4 Distribution ofmoinsture content inthe model
5.2 挡墙上的土压力分布模式
由于墙背土体的弹性模量随土体埋深变化而变化。在基本模型中,土表处因无竖向荷载故弹性模量为2 MPa,埋深3 m处的土体因竖向荷载近似为60 kPa,其弹性模量为17.1 MPa。因此为了方便计算,选取25 kPa下膨胀土的参数作为墙背土体的参数。
在不含EPS缓冲层的膨胀土悬臂式挡墙中,其土压力的计算与分布难以通过极限平衡理论精确计算。悬臂式挡墙会减小一部分土压力,再加之土拱效应的影响,使悬臂式挡墙上的土压力存在明显的非线性特点[5]。膨胀土膨胀前后在3种不同厚度挡墙下的墙背土压力和墙体位移如图5所示。
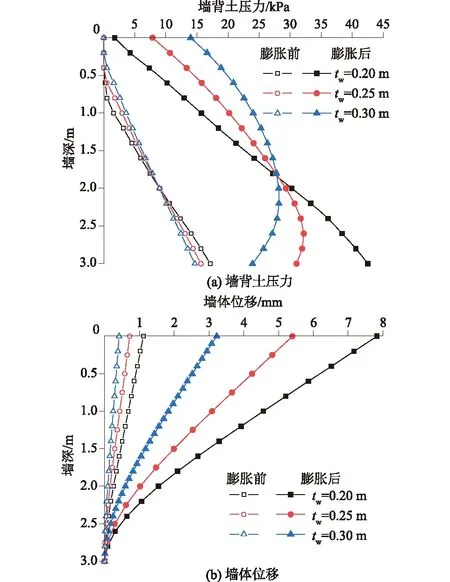
图5 墙背土压力和墙体位移分布 Fig.5 Distributions of lateral earth pressures of retainingwall and displacement of flexible retaining wall
膨胀土在增湿膨胀后由于墙体的约束产生了侧向膨胀力,且墙体越厚(相对柔度越小),约束膨胀土膨胀的能力越强,则土体侧向土压力逐渐增大;反之墙体厚度越小,膨胀土体增湿膨胀的能力越大,使得土体侧向土压力较小。另外土拱效应的特点使得土压力在一定深度处出现极值点。
由图5可以看出,膨胀土膨胀前后的墙背土压力和墙体位移有显著差异,在tw=0.20 m的挡墙下,膨胀土膨胀前仅由于土体自重产生了侧向土压力,在墙顶附近处其土压力为0;当膨胀土发生膨胀后,墙背土压力和墙体位移明显增加。因此膨胀土作用下的悬臂式挡墙对墙体位移会造成不利影响。较薄的挡墙厚度,即相对柔度越大,产生的墙体位移越显著。
膨胀土作用下悬臂式挡土墙在土体增湿后,土体会产生膨胀变形,悬臂式挡墙能为土体的变形提供空间,从而减小了作用在挡土墙上的膨胀力,并且当悬臂式挡墙的抗弯刚度越小,墙体变形的程度越大;若抗弯刚度无穷大的挡墙支挡膨胀土时,挡墙的变形近似为0,作用在挡墙上的土压力会增大。
5.3 EPS缓冲层参数分析
本小节探究了EPS缓冲层的厚度、弹性模量和摩擦特性对膨胀土悬臂式挡土墙上土压力的影响。采用式(7)、式(8)定义的侧压力合力减小率ip和倾覆力矩减小率im作为评估缓冲层减压效果的依据。
(7)
(8)
式中:p0、m0分别为不铺EPS缓冲层时墙背受到的总侧压力和倾覆力矩;p、m为铺设EPS缓冲层时墙背受到的总侧压力和总倾覆力矩。
5.3.1 EPS厚度
在基本模型中,取EPS15缓冲层,厚度为0.25、0.50、0.75 m,沿墙高均匀布置,探究在3种不同墙厚的基本模型中EPS厚度对墙背土压力的影响,如图6、图7所示,模拟结果见表5。
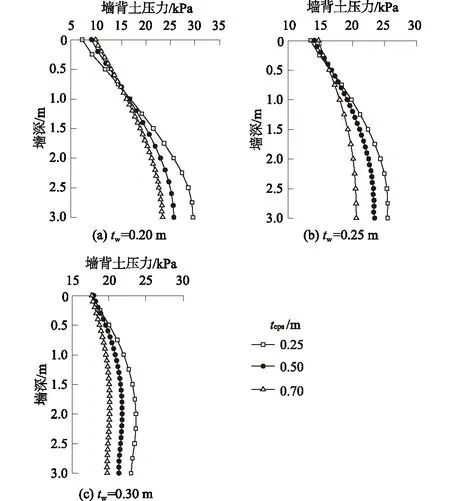
图6 挡土墙铺设不同厚度EPS时墙背土压力Fig.6 Distributions of lateral pressures of retainingwall with EPS buffer layer of varied thickness
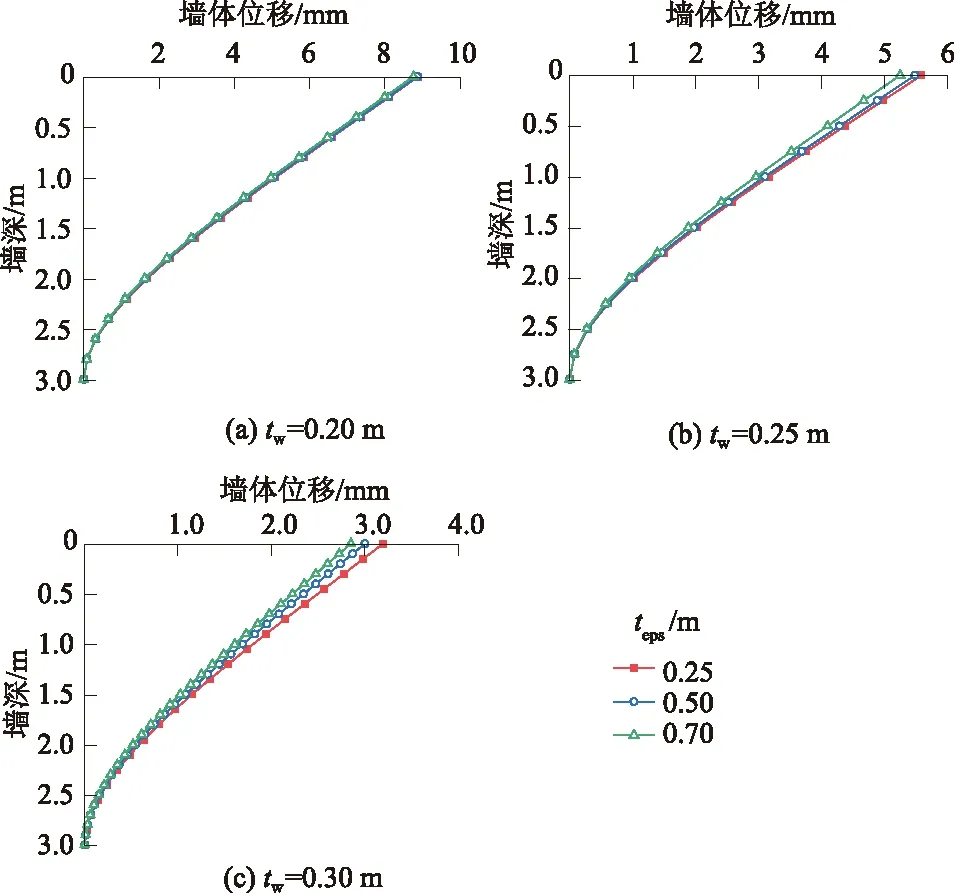
图7 挡土墙铺设不同厚度EPS时墙体位移Fig.7 Distributions of displacement of retaining wallwith EPS buffer layer of varied thickness
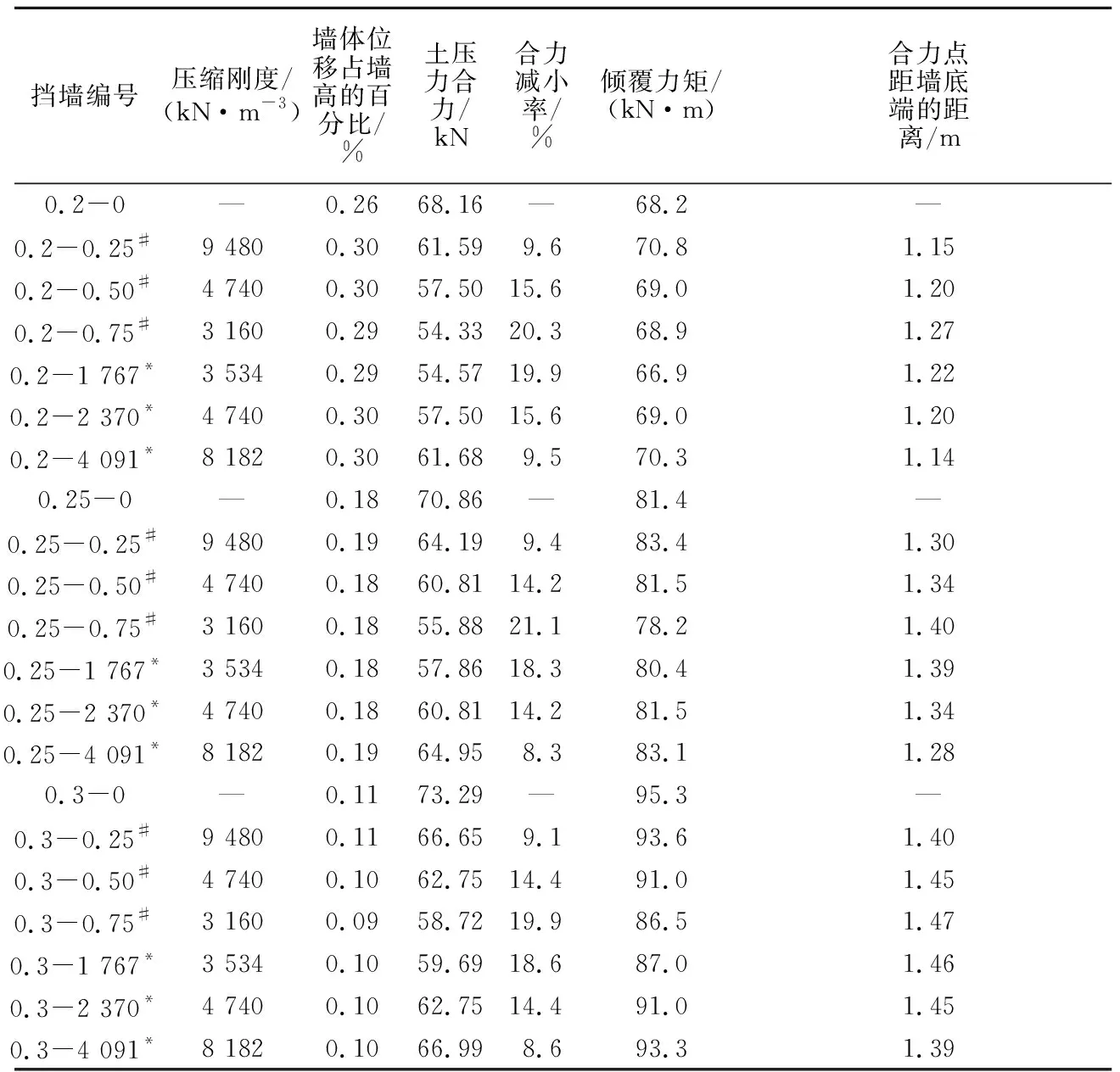
表5 不同参数的EPS缓冲层在不同挡墙上的减压效果Table 5 Pressure-reduction effectiveness of EPS bufferlayer with different parameters for retaining walls withdifferent flexibilities
从图6可知,挡墙顶处于自由端,膨胀土增湿膨胀后的侧向土压力会作用在挡墙上,并使之产生侧向位移;但随着EPS缓冲层厚度的增加,墙背土压力会因缓冲层的存在而发生应力重分布,相较于未铺设缓冲层时,侧向土压力分布较为均匀,并呈现出上部作用力小,下部作用力大的梯形分布。从图6发现,当EPS缓冲层厚度增大时,侧向土压力会有所减小,并且在墙体厚度较厚时,减小程度越大。
基本模型中可以将悬臂式挡墙看成一种悬臂梁,墙背膨胀土膨胀后墙背受到非均布荷载,当悬臂式挡墙侧铺设EPS缓冲层时,会使得墙背土压力重分布,墙体位移则与墙背土压力分布形式有关。由图7可知,有的铺设EPS缓冲层的体系所产生的墙体位移要比未铺设EPS缓冲层的体系时的大。根据结构力学中的图乘法可知,墙体位移与倾覆力矩和合力点的位置乘积有关。而在表5中,倾覆力矩的变化幅度较合力点位置的大,因此倾覆力矩的变化占主导地位,因此在表中当铺设EPS缓冲层时的倾覆力矩值大于(小于)未铺设缓冲层时,则会产生墙体位移大于(小于)未铺设缓冲层时的情形。
据表5可知,在悬臂式挡墙中,EPS厚度的增加,其压缩刚度K逐渐减小,使得土压力合力减小率得到增加,说明较低压缩刚度的缓冲层能提高其减载性能;但是压缩刚度的减小会增加墙背土压力合力点的位置,在一定情况下使倾覆力矩增加,甚至超过未铺设EPS缓冲层的情况,进而使墙体位移增加,因此在设计时要注意墙体位移的控制。
整体上看,厚度越厚的缓冲层会使得墙背土压力分布趋于均匀,且合力减小率逐渐增大,倾覆力矩以及墙体位移逐渐减小。
5.3.2 EPS弹性模量
同样在基本模型中,取0.5 m厚,具有3种不同弹性模量(1 767、2 370、4 091 kPa)的EPS缓冲层,其余条件均不变。探究在3种不同墙厚的基本模型中EPS弹性模量对墙背土压力的影响,如图8、图9所示,模拟结果见表5。
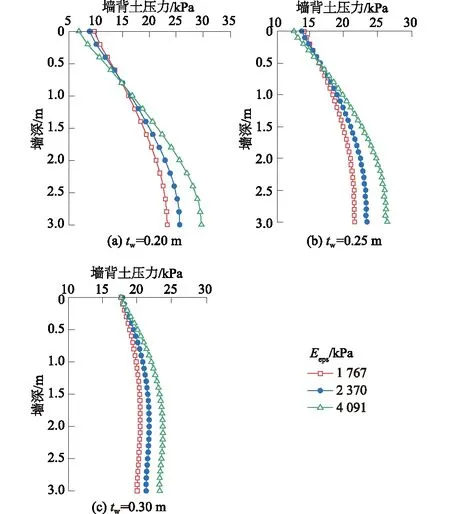
图8 挡土墙铺设不同弹性模量EPS的墙背土压力Fig.8 Distributions of lateral pressures of retaining wallin the presence of EPS buffer layer of varied elasticmodulus
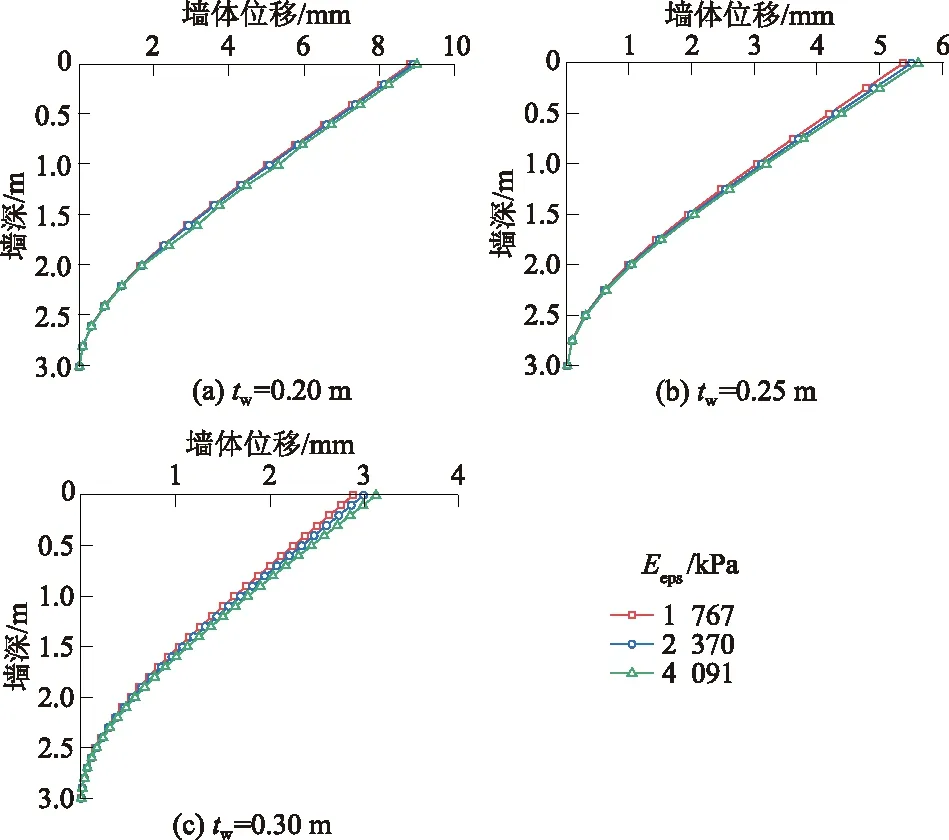
图9 挡土墙铺设不同弹性模量EPS时墙体位移Fig.9 Distributions of displacement of retaining wall inthe presence of EPS buffer layer of varied elastic modulus
由图8可知,膨胀土增湿膨胀后的侧向土压力作用在铺设EPS缓冲层的悬臂式挡墙上,其土压力经缓冲层的作用而发生重分布。当EPS缓冲层弹性模量增大时,墙背土压力会有所增加,并且在墙体厚度较厚时,这种增加会更加明显。另外从图9、表5发现,有的铺设EPS缓冲层的体系所产生的墙体位移要比未铺设EPS缓冲层的体系时的大。这说明,单一的改变EPS缓冲层的厚度或者弹性模量不能有效改善墙体位移的发展。将在5.4节对墙体位移进行详细讨论。
据表5可知,在悬臂式挡墙中,EPS弹性模量的减小,其压缩刚度K逐渐减小,使得土压力合力减小率得到增加,再次说明较低压缩刚度的缓冲层能提高其减载性能;倾覆力矩、墙体位移也随着EPS弹性模量的减小而减小,但在设计时也应注意控制墙体位移的发展。
对比3种不同墙体厚度的悬臂式挡墙,土压力的分布规律以及结论均与前一节较为相似,在此不再赘述。
5.3.3 界面摩擦
对于有明显竖向膨胀的膨胀土而言,EPS缓冲层与其他材料之间的界面摩擦是影响墙背土压力的重要因素,为了探究EPS缓冲层与膨胀土、挡墙之间的摩擦影响,考虑3种不同的算例:①EPS缓冲层与膨胀土、挡墙间均为光滑,记为S-1;②EPS缓冲层与膨胀土间的摩擦系数设为0.5,而与挡墙界面间的摩擦系数设为0.6,记为S-2[19];③EPS缓冲层与膨胀土间的摩擦系数设为0.5,而与挡墙界面间的摩擦系数设为0.3,记为S-3。
取墙体厚为0.2 m,EPS缓冲层厚为0.5 m且 弹性模量为2 370 kPa,考虑膨胀土体水平与竖向膨胀系数不相等的情况,得到模拟结果见表6。对于表6的3种算例,墙背土压力分布如图10所示。
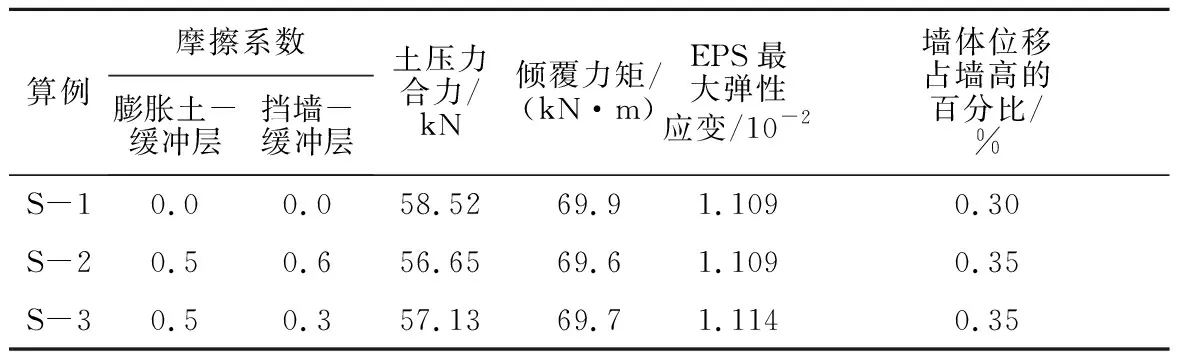
表6 考虑界面摩擦的模拟结果Table 6 Results of simulation in consideration ofinterface friction
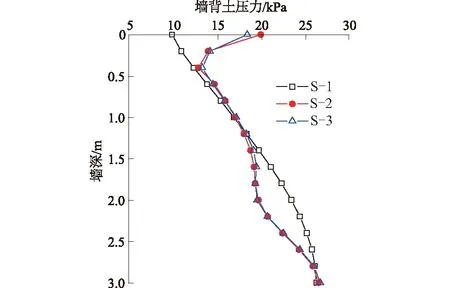
图10 考虑界面摩擦的墙背土压力分布Fig.10 Distributions of lateral pressures of retainingwall in consideration of interface friction
当不考虑摩擦因素的影响时,土压力的变化较为平缓,即图10中的S-1。当考虑摩擦因素影响时,作用在挡墙上的土压力变化较为剧烈,即图10中S-2、S-3,另外还可从图10看出S-2、S-3的土压力分布较为一致。以EPS缓冲层作为隔离体,进行受力分析可知,缓冲层因两侧的摩擦产生了力偶的作用,为了保持平衡使得EPS缓冲层两侧的受力出现重分布,上部土压力增大,而下部土压力减小。因此挡墙上部的土压力高于无摩擦的土压力,根据表6,倾覆力矩虽然没有太大变化,但是土压力合力点的位置明显比无摩擦的要高,因此墙体位移占墙高百分比较S-1大。
5.4 悬臂式挡墙的墙体位移分析
图11展示了在不同墙厚、不同缓冲层厚度及弹性模量下的墙体最大水平位移分布,以此显示墙体位移在3种因素下的影响。图中的水平基准面表示的是3种墙体在不铺设EPS缓冲层时的墙体最大位移占墙高的百分比值z,即当tw=0.2 m时,z=0.261%;当tw=0.25 m时,z=0.18%;当tw=0.2 m时,z=0.108%。
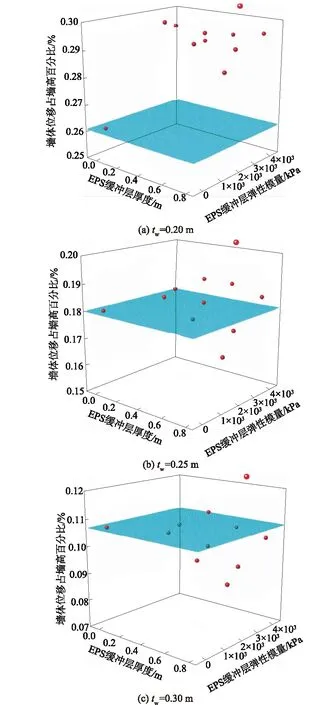
图11 不同EPS缓冲层参数下墙体最大水平位移分布Fig.11 Distribution of maximum horizontal displace-ment of retaining wall with varied inclusion parameters of EPS buffer layer
由前可知,墙体厚度是关系到墙体水平位移的重要因素,墙体厚度越小,水平位移越大。在墙体厚度为0.2 m的墙体中,任意EPS缓冲层参数之间的组合都不能使墙体位移占比低于不铺设EPS缓冲层的墙体位移占比,根据4.3.1节的分析,即在厚度较薄的悬臂式挡墙铺设EPS缓冲没有意义。但在墙厚0.25 m的墙体铺设EPS缓冲层时,teps=0.5 m、Eeps=1 767 kPa;teps=0.75 m、Eeps=1 767 kPa;teps=0.75 m、Eeps=2 370 kPa,这3种情况下的墙体位移占比低于不含EPS的情况。从这一点可以说明,厚度较厚且弹性模量较小的缓冲层较为适用。在墙厚为0.3 m的墙体铺设缓冲层时,除了teps=0.25 m、Eeps=4 091 kPa以外,其他的墙体位移都能在不铺设缓冲层时墙体位移占比之下。
综上所述,在影响墙体位移占比因素中,墙体厚度的影响程度最大,EPS缓冲层厚度与弹性模量次之;并且当厚度较厚、弹性模量较低时,EPS缓冲层才会起到控制墙体变形的作用。
5.5 EPS缓冲层的减压效率规律
根据5.3.1节与5.3.2节的分析,可以得到悬臂式挡墙铺设EPS缓冲层后,墙背土压力合力减小率有不同程度的增加。大体可以得出合力减小率随着缓冲层厚度的增加而增加,但随着缓冲层弹性模量的增大而减小。而压缩刚度K可以较好地反映两种参数之间的关系,图12为合力减小率与压缩刚度之间的关系。由图12可见,墙背土压力合力的减小率与压缩刚度成反比,其中线性拟合相关参数见表7。从表中的确定系数(R2)可以看出,拟合结果较好。另外,在不同墙厚的悬臂式挡墙中,其截距、斜率大致相近,因此在设计中可按照其二者的关系,预测其合力的减小率。
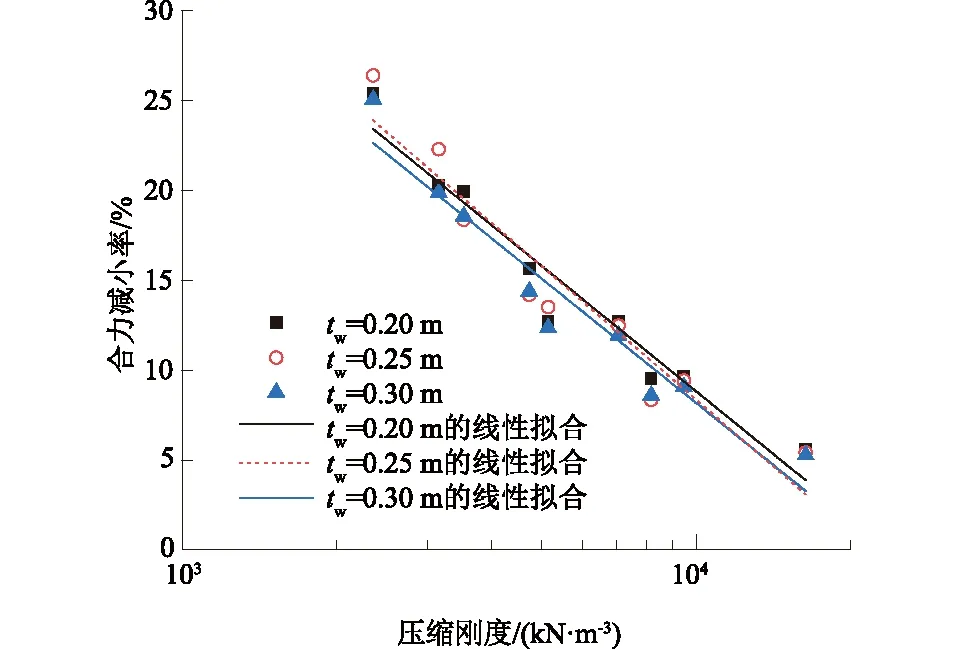
图12 墙背土合力减小率与缓冲层压缩刚度的关系Fig.12 Relation between the rate of resultant forcereduction and the compression stiffness of EPS

表7 不同墙厚下的拟合参数Table 7 Fitting parameters under varied thickness of retaining wall
6 结 论
本文通过一系列的数值模拟,研究了膨胀土-EPS缓冲层-悬臂式挡墙体系的工作性能,探讨了EPS缓冲层的相关参数、悬臂式挡墙厚度的影响,可以得到以下结论:
(1)在悬臂式挡墙模型中,墙背土压力合力随着EPS缓冲层厚度的增加而逐渐减小,合力减小率增大;但墙背土压力合力随着EPS缓冲层弹性模量的增加而增加,合力减小率变小。因此缓冲层宜选用低弹性模量和高厚度的EPS。
(2)EPS缓冲层与膨胀土、挡墙之间的界面摩擦不会明显改变墙背土压力合力以及倾覆力矩,但会使墙背土压力出现重分布,上部的侧压力增加,下部的侧压力减小。
(3)含EPS缓冲层的悬臂式挡墙相互作用机理是EPS缓冲层可为膨胀土增湿膨胀提供空间,从而减小膨胀土压力。膨胀土压力在EPS缓冲层的作用下发生了重分布;墙体厚度是控制墙体变形的关键因素,在厚度较大(tw≥0.25 m)的悬臂式挡墙下,厚度厚、弹性模量小的缓冲层能有效减小悬臂式挡墙的侧向位移。
(4)在悬臂式挡墙中,EPS缓冲层的减压效率与EPS缓冲层压缩刚度呈负相关,可以预测EPS的减压情况。

