基于变量筛选优化极限学习机的混凝土坝变形预测模型
曹恩华,包腾飞,胡绍沛,袁荣耀,鄢 涛1,2,
(1.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098; 2.河海大学 水资源高效利用与工程安全国家工程研究中心,南京 210098; 3.河海大学 水利水电学院,南京 210098; 4.三峡大学 水利与环境学院,湖北 宜昌 443002)
1 研究背景
作为重要的基础设施,混凝土坝在发电、防洪、灌溉和供水等方面发挥了重要作用[1-2],对其结构性态的准确预测是保障其安全运行的重要措施[3]。作为大坝结构性态最直观、最有效的反映,变形已经被广泛用作混凝土坝的主要监测指标[4-6]。基于变形监测数据建立可靠的预测模型,是大坝安全监控领域重要研究方向之一。
变形反映了在内、外部环境的影响下,大坝结构的非线性动态演化[7-8]。相关的监控模型主要分为3种:统计模型、确定性模型和混合模型[4,7,9-11]。确定性模型需要尽可能精确的材料参数、几何形状,以及大坝和地基的工作条件,这在实际工程中难以实现[11]。统计模型无需考虑大坝和坝基的物理特性,因此更易于实施[12],它是大坝变形监测中最为常用的建模方法;但是,统计模型的泛化能力和预测时延性较差,使得此类模型在实际应用中效果并不理想[13]。
近年来,随着人工智能技术的发展,人工神经网络(Artificial Neural Network,ANN)和支持向量机(Support Vector Machine,SVM)等算法已广泛应用于大坝变形监控领域[14-18]。然而上述算法也存在一定的局限性,如收敛速度缓慢、容易陷入局部极小值以及核参数难以选择等。为了避免上述问题,本文选取极限学习机(Extreme Learning Machine,ELM)作为大坝变形的基础预测模型。ELM是由Huang等[19]于2006年提出的一种新型单隐含层神经网络,该算法能够随机生成输入层与隐含层之间的连接权重以及隐含层神经元的阈值,且在训练过程中无需调整,只需要设置隐含层神经元的数量即可获得理想的输出。与ANN、SVM等算法相比,ELM具有简单易用、收敛速度快以及泛化能力强等优点[4]。
本文中,ELM模型的输入向量通过统计模型HST(Hydraulic-Season-Time)获取。HST通常会引入较高维度的变量,在机器学习过程中,这些变量并不是同等重要的,不相关变量将使得模型更为复杂,进而增加过拟合风险、影响预测性能。若能够筛选出具有代表性的变量,消除不相关的变量,则可以降低模型复杂度从而提高预测精度。Dombi等[20]提出使用平均影响值(Mean Impact Value,MIV)来反映神经网络中权重矩阵的变化,这是评估神经网络变量相关性的最佳指标之一。MIV算法通过计算输入变量增加(减少)之前(之后)的模型输出变化来衡量变量的相关性,从而筛选出与因变量高度相关的因子。本文结合MIV与ELM算法的特性,对各变量的重要性进行排序,从而筛选出具有代表性的最简输入变量集。为进一步提高筛选出的变量可信度,本文提出采用基于MIV排序的反向逐变量剔除法,通过对应ELM模型的输出精度变化来验证并确定最佳输入变量集,这一操作可以提高变量筛选的可靠性。
本文着重研究以下4个主题:①结合理论分析与监测数据建立混凝土坝变形统计模型,确定初始变量集;②基于MIV-ELM模型量化各变量重要性,采用正反分析法确定最佳输入变量集;③基于筛选出的最佳变量集和确定的ELM网络结构进行混凝土坝变形分析;④验证提出模型的可拓展性。
2 变量筛选理论
2.1 极限学习机
极限学习机(ELM)是由Huang等[19]于2006年提出的新型前馈神经网络,由输入层、隐含层和输出层组成。对于N组样本(xi,ti(i=1,2,…,N)),其中xi和ti分别为神经网络的输入样本和输出,假设隐含层激活函数为g(x),则包含l个隐含层神经元的模型输出为
(1)
式中:bi为i个隐含层神经元的阈值;ωi和βi分别为神经网络的输入、输出权重。式(1)可以表示为
Hβ=T′ 。
(2)
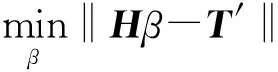
(3)
式中yi为神经网络的期望输出。
2.2 基于MIV-ELM的变量筛选
基于变量筛选方法剔除不相关变量,可以提高模型的准确性,并降低模型过度拟合的风险。Dombi等[20]提出使用MIV来反映神经网络中加权矩阵的变化,MIV的主要原理是通过相应神经网络的输出来确定自变量对因变量的影响程度。当模型输入发生轻微变化时,影响程度用MIV指数表示,符号代表相关方向,绝对值代表影响度。本文将混凝土坝的变形监测数据分为训练集F和测试集T,首先将训练集中的每个独立变量在原值的基础上加/减10%,形成2个新的训练样本F1和F2(每次改变其中一个变量,其他变量保持原值)。然后使用ELM分别对F1和F2进行建模并预测,得到预测结果A1和A2,二者差值即为该变量对模型输出影响的变化值(IV)。MIV-ELM结构如图1所示。
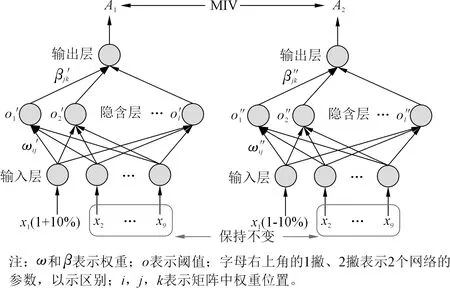
图1 MIV-ELM模型结构Fig.1 Structure of the MIV-ELM model
基于观测次数对IV进行平均得到各变量对应的MIV,根据其绝对值大小对变量进行排序,当变量的累计贡献率达到限定条件时,完成变量选择,获得最佳输入变量集。各个自变量对输出的相对贡献率和累积贡献率可根据式(4)和式(5)计算得到,即:
(4)
(5)
式中:m为总的变量个数;n为当前叠加变量个数;γi为第i个变量对因变量的相对贡献率;μ是前n个变量的累积贡献率。综上所述,本文提出的HST-MIV-ELM算法流程如图2所示。本文选用了均方根误差RMSE、平均绝对误差MAE、决定系数R2、均方误差MSE、相关系数R及均方根偏差RMSD等指标对模型进行全面评价。
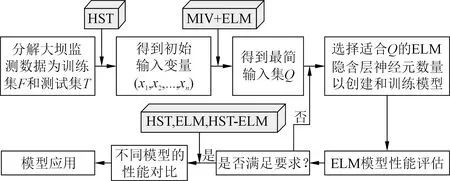
图2 HST-MIV-ELM模型流程Fig.2 Flow chart of the HST-MIV-ELM model
3 应用实例
3.1 工程概况
以某碾压混凝土重力坝为例,其最大坝高为72.4 m,该坝变形监测系统包括水平位移和垂直位移。选取第4坝段EX5测点对应的位移相关监测数据构建模型并分析模型的预测性能。数据范围为2016年6月6日至2018年10月22日期间的739组数据(日观测),位移和水位变化过程线如图3所示,其中训练集F对应1~709次监测数据,其余部分设为测试集。
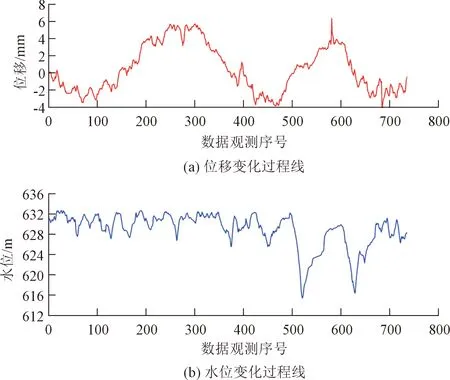
图3 EX5测点的位移和水位变化过程线Fig.3 Variations of displacement and water level at monitoring point EX5
3.2 获取初始变量
基于HST模型理论[13],可以确定本文研究坝型的统计模型因子,如表1所示。其中,ai、b1i、b2i和ci分别表示对应项的系数,H为观测日上游水深与基准日上游水深的差值,t表示从基准日到观测日的累计天数,θ表示时效因子,且θ=t/100。由此确定的模型初始变量集以及通过多元线性回归得到的各系数值见表1。

表1 HST系数值及相应影响因子Table 1 HST coefficient values and corresponding impact factors
HST对应的拟合和预测过程如图4所示。由图4可以看出,HST模型的拟合结果与真实值趋势大致相同,但效果并不是很理想;该模型在测试集上的结果与实际值相差较大,说明对于本节研究的案例,HST并不能很好地描述大坝变形。
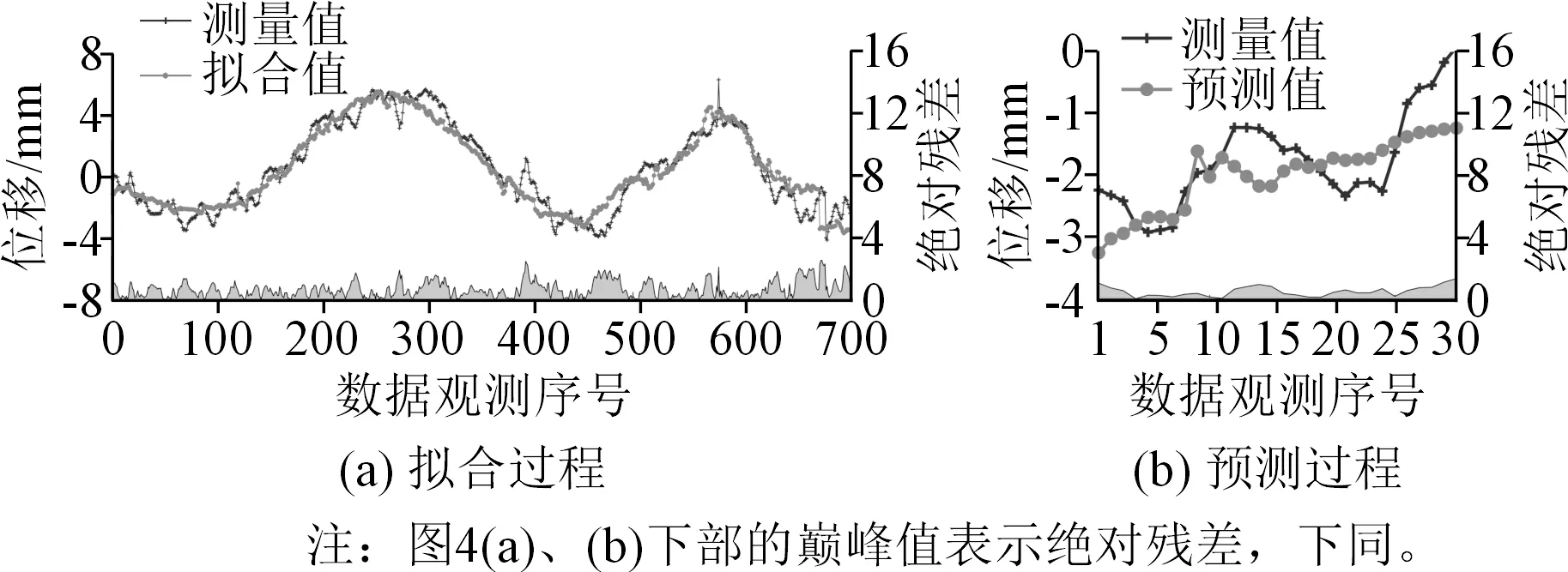
图4 HST的拟合和预测结果Fig.4 Fitted and predicted results of HST
3.3 变量提取
在ELM模型的基础上,采用MIV算法分析上节中9个变量对变形的影响程度。通过分析,选择水平位移累计贡献率μ在0.950 2以上的变量作为ELM模型的输入变量。各变量的|MIV|排序及对应的μ值分别见图5和表2,其中x1—x9分别对应表1中的9个因子。可以看出,当μ达到0.950 2时,共筛选出7个变量,即(x4,x5,x6,x8,x9,x3,x2)。
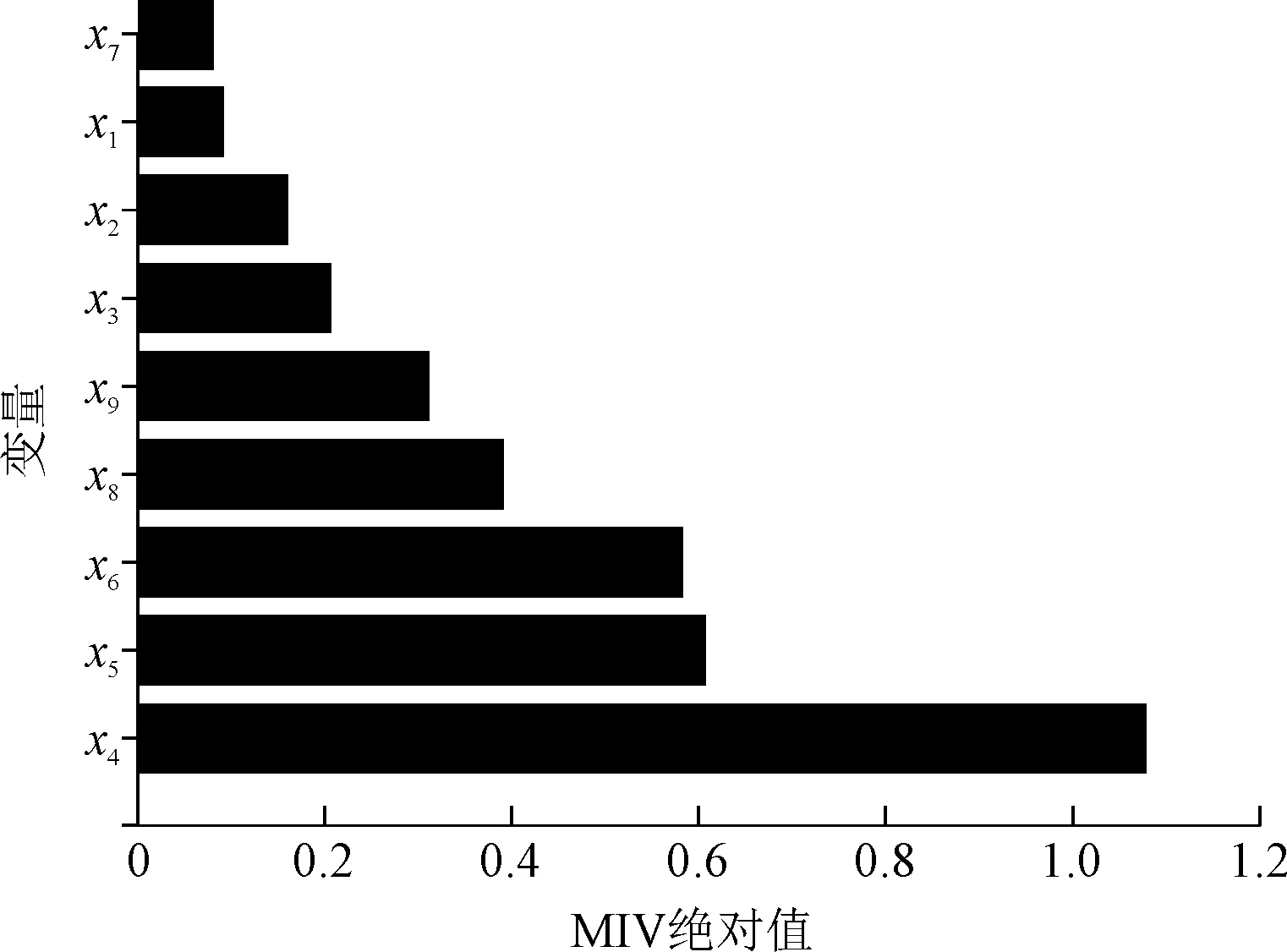
图5 基于MIV的变量排序Fig.5 MIV-based variable ranking
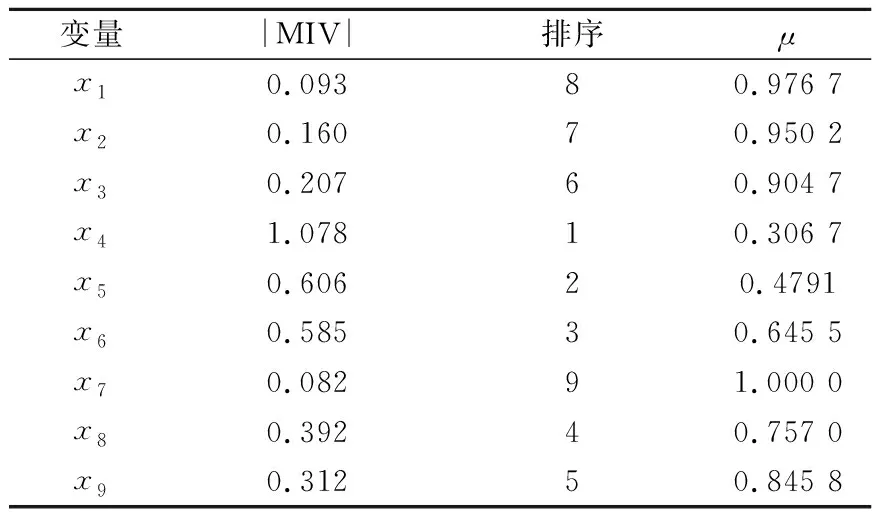
表2 变量累计贡献率Table 2 Cumulative contribution of variables
3.4 反向逐变量剔除法
由于ELM的学习过程有一定的随机性,为进一步验证本文3.3节筛选的输入变量集的可靠性,本节提出了反向逐变量剔除法,即根据各个变量的MIV排序逆向逐个剔除,并选取均方误差(Mean Square Error,MSE)作为评价指标量化剩余变量对应的ELM模型精度。计算结果见图6。
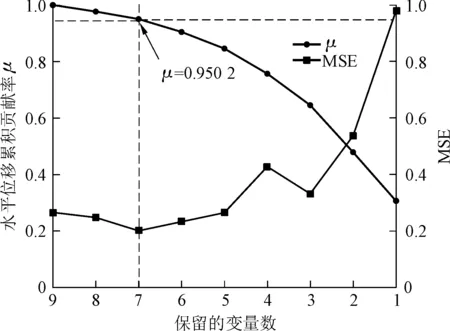
图6 反向逐变量剔除结果Fig.6 Results of reverse variable-by-variable elimination
从图6可以得出结论:不同变量组合的输出结果对应的MSE值呈现先下降后上升的趋势。随着与变形不相关或相关性较小变量的剔除,模型的预测精度呈上升趋势,当某一变量被剔除后,模型的精度达到最高水平,若继续剔除剩余变量,预测精度开始下降。可以看出,当剔除变量x1后,模型的预测精度达到最高,说明3.3节中7个变量组成的输入变量集是有效的,该方法弥补了ELM随机性带来的不确定性,使得筛选结果更加可靠。
3.5 确定ELM网络结构
以(x4,x5,x6,x8,x9,x3,x2)为输入、水平位移为输出构建ELM模型,首先应当确定模型的网络结构以便得到最佳的输出结果。结合前文所述,模型的输入层共有7个神经元,输出层有1个神经元,选取Sigmiod函数作为模型的激活函数。同时,ELM的预测性能很大程度上取决于隐含层神经元个数l,它对模型的预测准确性有很大的影响[4]。通过分析,当l取值超过60,模型的模拟精度明显降低。因此本文采用区间分割方法分析了l∈[1,60]时隐含层神经元个数对模型预测结果的影响,即每次取靠近区间中间的点作为l的取值并参与建模和验证模型性能,然后将该点作为区间分割点,并成为下一个区间的左(右)边界,重复该操作直到遍历所有取值。选取MSE和R2作为性能评价指标,分析结果如图7所示。从图7可以看出,当l=40时,模型得到最小MSE值和最大R2,说明此时ELM模型性能最佳。
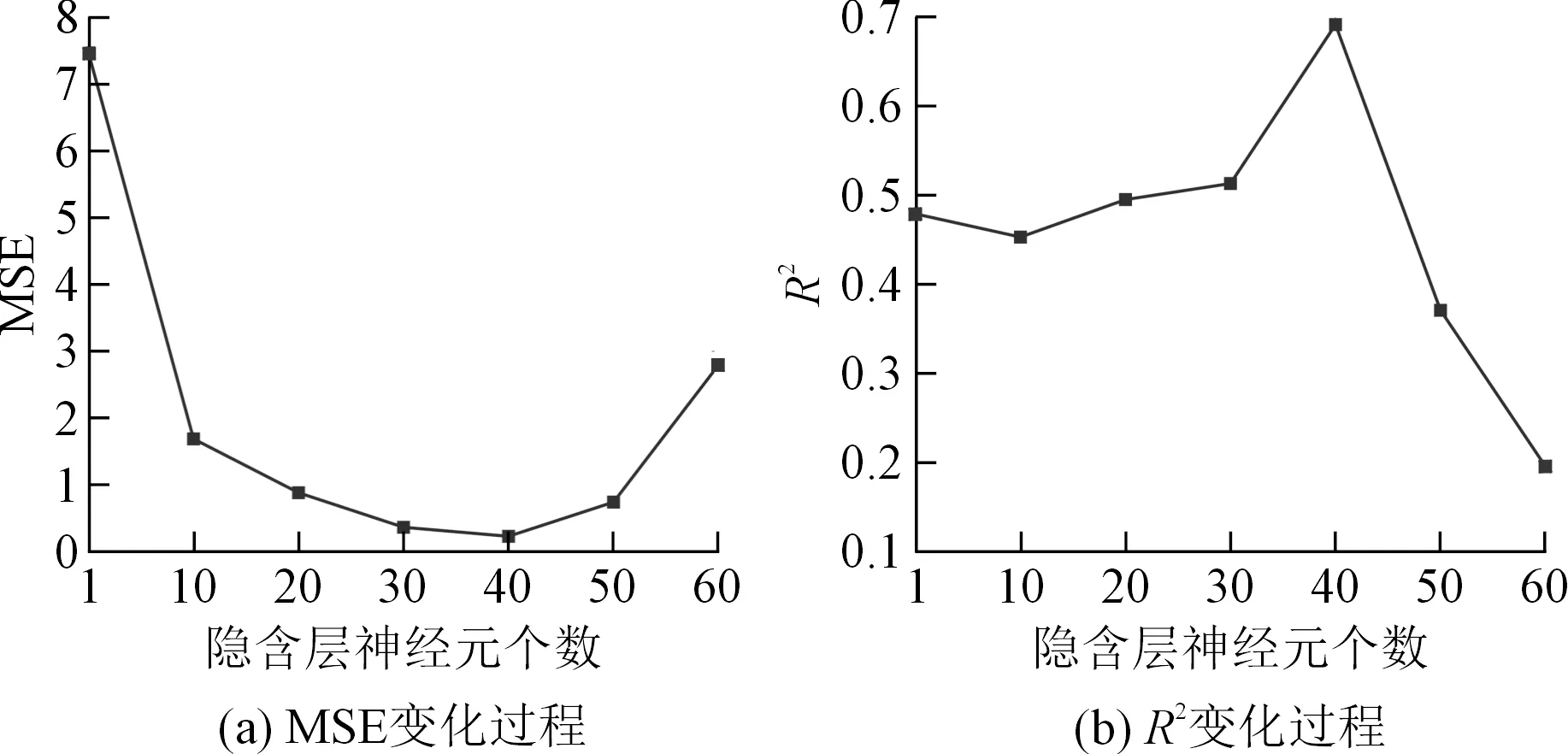
图7 隐含层神经元个数的确定过程Fig.7 Process of determining the number of neurons in the hidden layer
3.6 模型性能比较
选取大坝变形领域的常用模型(HST、ELM和HST-ELM)与HST-MIV-ELM模型进行比较,以验证后者在大坝变形预测中的优越性。通过HST、ELM同HST-ELM的对比,可以验证基于统计模型确定模型输入的有效性;HST-ELM与HST-MIV-ELM的对比,可以证明基于MIV-ELM的变量筛选方法的可靠性。各模型的拟合、预测过程见图4和图8,为了更加直观地评价各模型性能,本文采用了RMSE、MAE和R量化模型的拟合和预测结果[4],具体见表3。
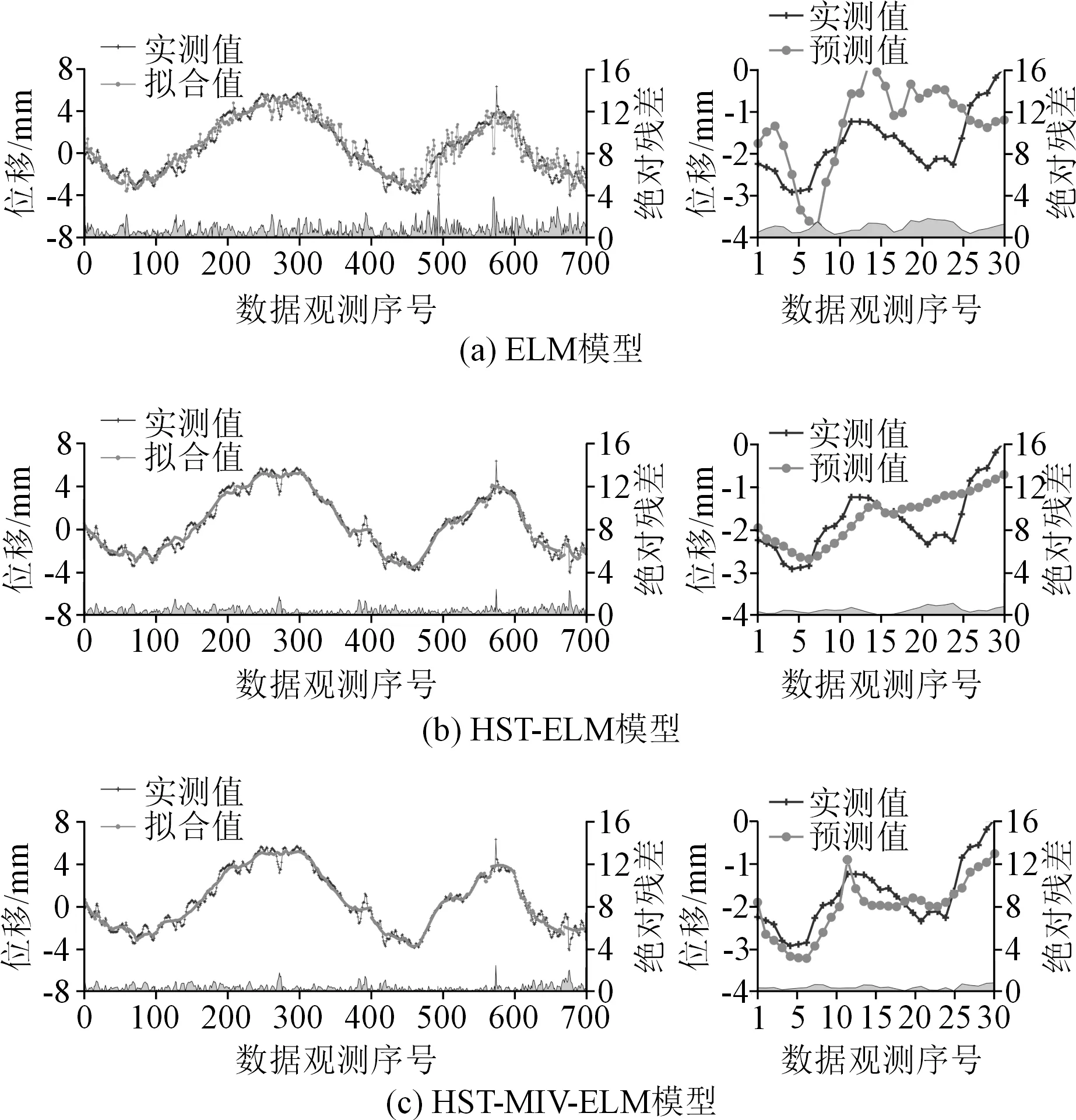
图8 各模型的拟合和预测结果Fig.8 Fitted and predicted results of each model
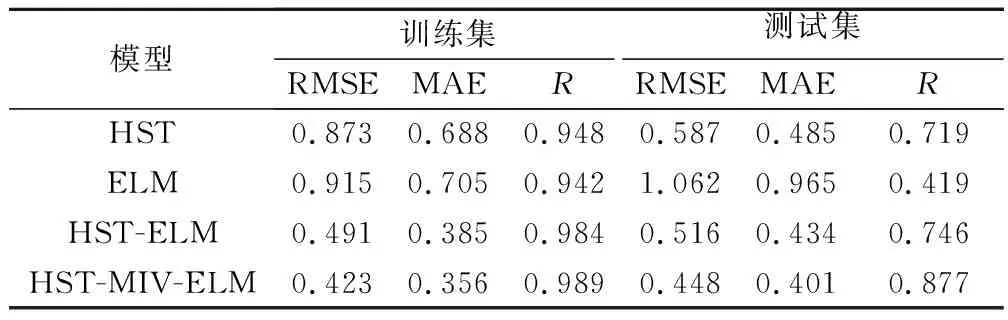
表3 各模型性能评价指标Table 3 Values of performance evaluation indicators for each model
从图8和表3可以看出,ELM模型在训练和测试阶段的性能远低于其他模型,HST次之,说明单一的统计模型或机器学习算法往往并不适用于非稳定、非线性较强的大坝变形预测。相比之下,经过HST优化的ELM不论在训练阶段还是在测试阶段都表现出了较好的性能,其绝对残差面积也明显小于单一模型。与精度较高的HST模型相比较,HST-ELM在测试阶段的RMSE、MAE和R值分别为0.516、0.434和0.746,同比RMSE和MAE分别降低了12.1%、10.52%,同比尺提升了3.76%。说明通过HST提取模型输入变量是切实可行的,其能够在一定程度上提升模型预测精度。然而,由图8(b)和表3可以看出,HST-ELM模型在测试阶段的效果并不是很好,预测结果在变化幅度较大节点上的变化趋势差异较大。对比分析HST-MIV-ELM,它在训练阶段和测试阶段的绝对残差都是最小的,且各指标均有明显的提高。与HST-ELM相比,其RMSE、MAE分别降低13.18%和7.6%,R提升了17.56%。说明本文提出的变量筛选方法能够有效地剔除不相关变量,保留对结果影响较大的变量,从而提高模型的准确度和可靠性。为了更加直观地对比分析各个模型的性能,图9和图10分别为各模型位移预测结果的对比和泰勒图。
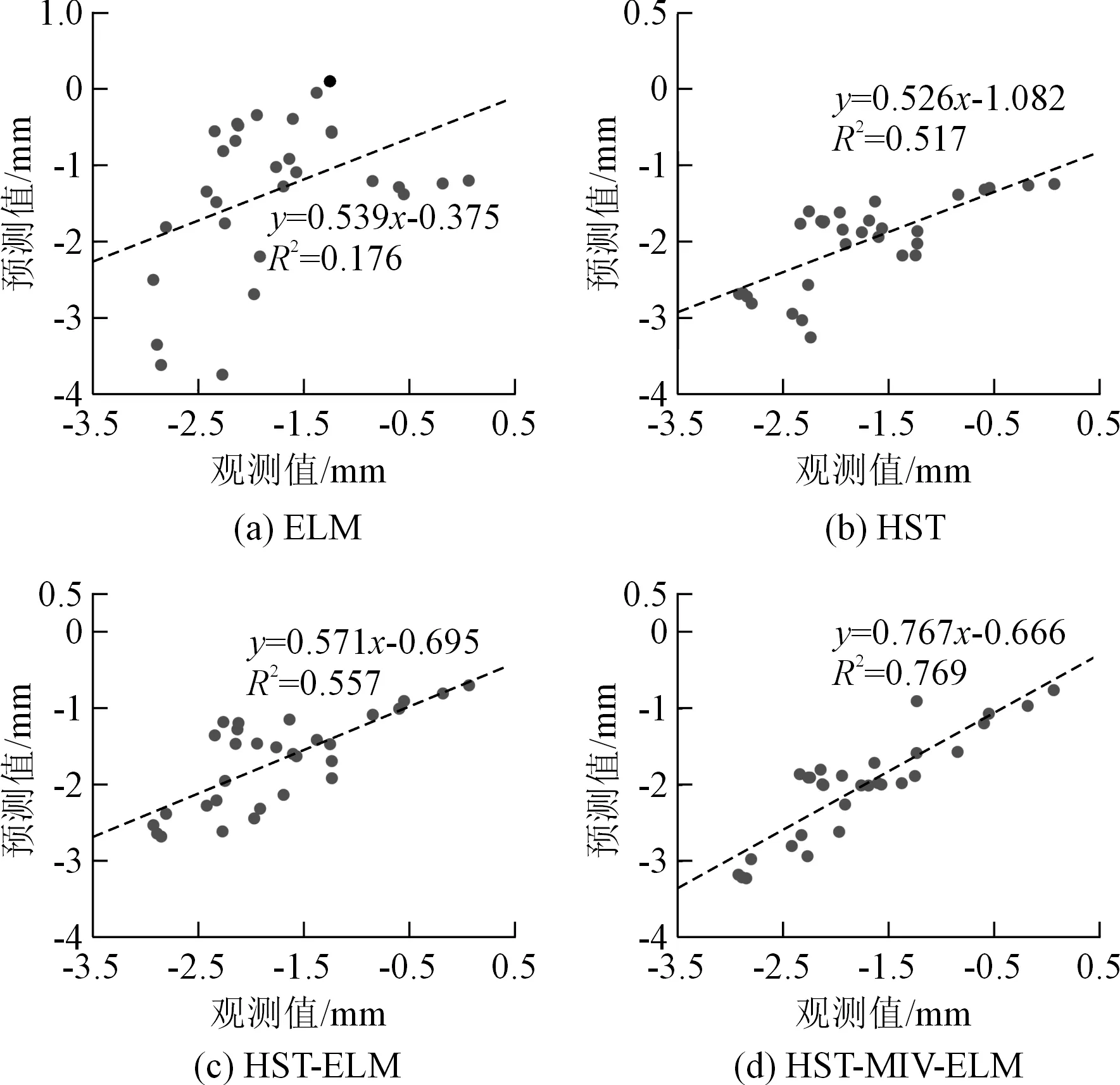
图9 不同模型位移预测结果Fig.9 Comparison among different models in testing phase
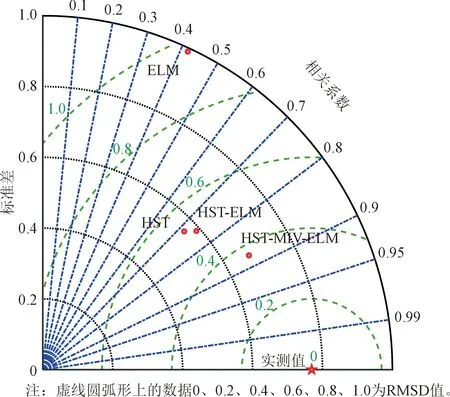
图10 各模型位移预测值泰勒图Fig.10 Taylor diagram of the predicted displacement values for each model
很明显,ELM模型对应的决定系数过小,因此对于变形数据波动性较大的混凝土坝工程来说,单一的神经网络在温度测值不完整的大坝变形分析中是没有意义的。HST-ELM的性能均优于ELM,说明基于HST模型提取的输入变量对提高ELM模型性能有着重要作用。变量筛选后模型的预测精度进一步提高,说明MIV对提高模型整体性能具有重要意义。由泰勒图可以看出,HST-MIV-ELM的综合指标最接近真实值,可以得出与上文中同样的结论。
4 模型可拓展性验证
通过上文分析,HST-MIV-ELM的性能优于传统变形预测模型。为了验证该模型在大坝变形预测中的可拓展性,本节从预测时延性和适用性2个方面进行了分析。
4.1 预测时延性验证
为了验证所提出的模型对大坝变形的长期预测效果,我们依次以2018年10月22日之后的60组、90组、120组和150组观测数据作为模型测试集,分别构建HST-MIV-ELM模型。表4为各试验组对应的性能评价指标。由表4可以看出,HST-MIV-ELM可以较好地预测大坝变形的周期性行为。
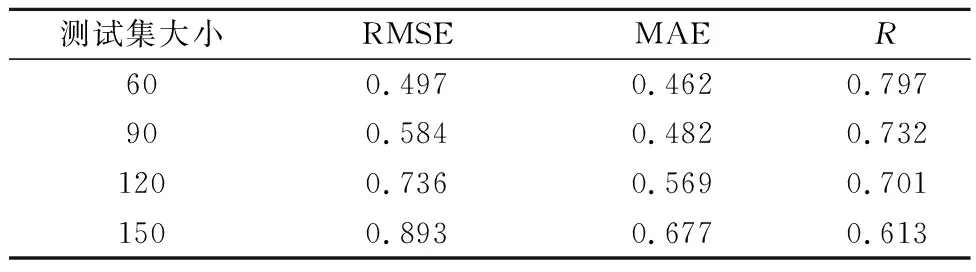
表4 不同时长预测结果评价指标值Table 4 Values of evaluation indicators corresponding to different forecast lengths
4.2 适用性验证
为了验证本文提出的模型广泛适用于不同的混凝土坝型,以某混凝土双曲拱坝为例,说明模型的有效性。选取该坝PL11-1测点对应的900个变形作为分析对象,变形和水位变化过程线如图11所示。其中1~800组数据作为训练集,801~900组数据作为测试集。
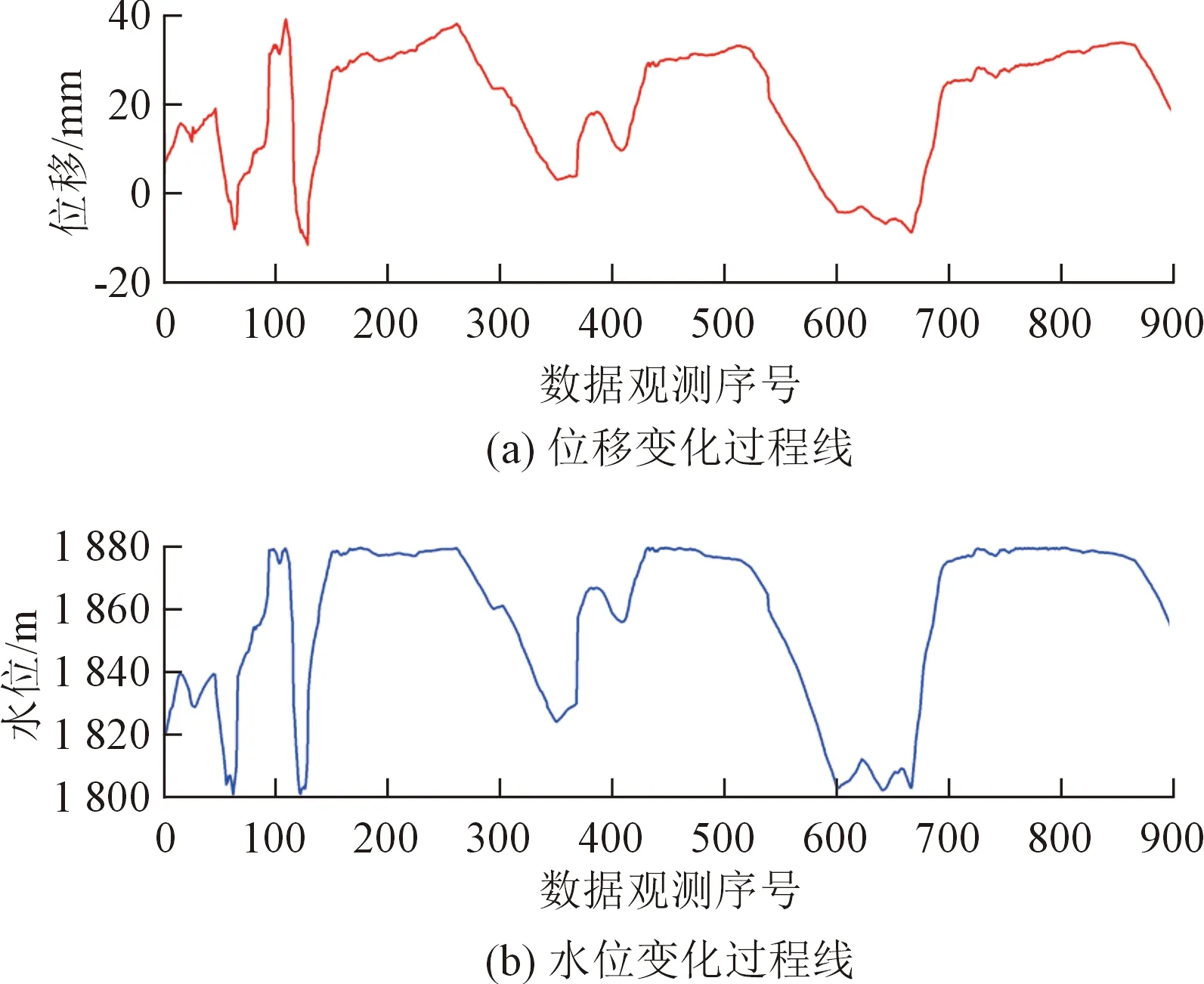
图11 PL11-1的位移和水位变化Fig.11 Variations of deformation and water level at monitoring point PL11-1
首先通过MIV方法对初始输入变量进行筛选,确定变量筛选结果为(x1,x8,x4,x5,x6,x7)。基于变量筛选结果,构建HST-MIV-ELM模型,并与HST、ELM以及HST-ELM的预测结果进行对比。各模型预测结果及性能评价指标分别如图12和图13所示。
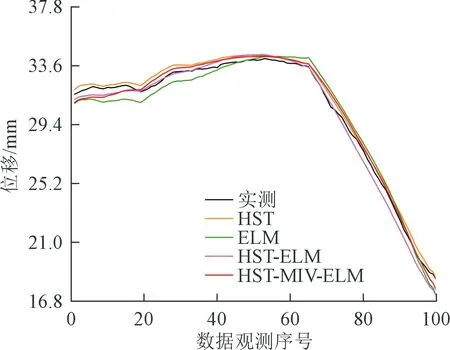
图12 各模型的预测结果Fig.12 Prediction results of each model
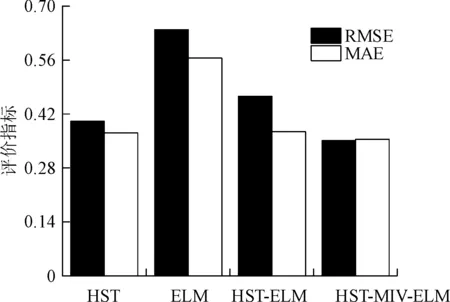
图13 各模型RMSE和MAE对比Fig.13 Comparison of RMSE and MAE among different models
可以看出,受原始数据波动性的影响,各模型针对PL11-1测点建模得到的预测结果均取得了较好的效果,预测值的变化趋势接近真实值。图13表明,HST-MIV-ELM模型对应的RMSE与MAE均是最小的,说明该模型的预测性能优于其他模型。
5 结 论
本研究提出了一种新型的混凝土坝变形预测模型,该模型基于HST、MIV和ELM模型三者的结合,主要结论总结如下:
(1)提出的MIV-ELM变量筛选法可以一定程度上降低模型的复杂度,提高模型的预测性能和预测性能。
(2)传统的预测模型更适用于数据波动性较小的变形预测,本文提出的HST-MIV-ELM模型针对不同坝型、不同波动程度的原始数据,均能较好地模拟和预测大坝变形,具有较强的稳健性。
(3)从预测时延性和可拓展性2个角度验证了HST-MIV-ELM模型的性能。结果表明,提出的模型对不同混凝土坝工程具有较强的适用性。

