基于时变Budyko模型的滹沱河上游径流变化归因分析
苗正伟,路 梅,丁志宏
(1.河北水利电力学院 水利工程学院,河北 沧州 061001; 2.中水北方勘测设计研究有限责任公司,天津 300222)
1 研究背景
受气候变化和人类活动等因素的影响,径流的非平稳性在全球范围内已普遍存在[1],这对水资源的规划与管理提出了严峻挑战,识别径流变化的影响因子是应对这种挑战的主要任务之一。近些年来,学者们通过水文模型法[2-4]、Budyko框架分析法[5-6]、经验统计法[7-8]等多种方法进行径流影响量化分析,其中,基于Budyko模型方法相对简单,且已被多项研究证实其结果是稳定、可靠的[6,9]。敏感性分析法[10]和分解法[11]是基于Budyko框架分析流域年尺度上径流变化原因的两种主要方法。其中,分解法可以独立地估计影响因子对径流变化的贡献率,而无需计算敏感性系数[12],因此更为简单、直观。
在分解法中,影响径流的因素主要是干旱指数(潜在蒸散发与降水的比值)和方程参数。很多研究[9,13-15]将这二者分别视为气候变化和人类活动的表征。但是,干旱指数仅仅是潜在蒸散发与降水的比值,其他诸如降水的季节性、降水强度、气温等气候特性也会对流域的产流过程产生影响,但它们并未包含于干旱指数,因此,干旱指数不能完全代表气候变化。另一方面,单参数Budyko方程中的参数一般与地形、土壤、植被等流域特征有关[16],它在某种程度上可表征人类活动对径流的影响,但有研究表明,降水等气候因素也可以通过改变方程参数而间接影响径流变化,因此,该参数其实是人类活动和气候变化对径流影响的综合表征[12,17]。鉴于此,基于单参数Budyko方程,本研究将径流影响因素直接划分为“干旱指数”和“流域特征”两类,而不将之称为气候变化和人类活动。
以前基于Budyko假设的径流变化归因分析一般基于径流序列的突变点划分基准期和变化期,然后用各时段的水文气候要素均值拟合Budyko方程,进而采用分解法或敏感性分析法进行径流影响分离[13,18-19]。但该过程存在2点不足:①在基准期和变化期,Budyko方程参数均被视为常数,这意味着干旱指数和流域特征对径流的影响是在突变点处突然发生的,这显然不符合实际,两者对径流的影响是逐渐发生的,而不是一蹴而就的;②有些流域的径流序列虽然呈现显著趋势,但没有显著突变点,此时,该方法适用性受限。
鉴于前人研究中存在的上述问题,本文构建时变Budyko方程在年尺度上量化干旱指数和流域特征对径流的影响。首先,在小波分析的基础上对水文气象序列进行滑动处理;然后以时间为协变量,描述Budyko方程参数及气候因子的时间变化,进而构建时变Budyko方程;最后基于分解法在年尺度及多年尺度上分离干旱指数和流域特征对滹沱河上游流域径流变化的影响。
2 研究方法与数据来源
2.1 研究方法
2.1.1 时间序列的滑动平均处理
Budyko方程需要耦合水量平衡方程才能对径流进行模拟,为了满足流域蓄水变量可以忽略的前提条件,首先对原始水文气象时间序列进行滑动平均处理。但对滑动窗口宽度的选择,目前并无统一标准,主观性较强[12,20-21]。考虑到径流变化归因分析的本质在于探究径流影响因子对径流长期变化趋势的影响,这就需要消除时间序列的周期性波动和随机性成分。因此,首先采用小波分析法对原时间序列进行周期性分析,然后进行滑动平均处理,这样,既能弱化周期性成分的影响,又能满足流域蓄水变化量近似为0的前提条件。基于复Morlet小波分析法[22]的结果表明:滹沱河上游流域的降水、潜在蒸散发、年径流深系列的第一主周期尺度上的平均周期长度分别为8.3、7.8、10.2 a,在此基础上,综合考虑观测数据长度以及便于表达的原则,最终确定对原序列进行11 a滑动平均处理,并将其记为
(1)
式中:i为原始时间序列的时序;xi为第i年的原始水文气象要素值;t为11 a滑动平均处理之后的时间序列的时序;yt为11 a滑动平均处理后的第t年的水文气象要素值。
2.1.2 气候变量模拟
滑动平均处理在某种程度上弱化了周期性波动的影响,而时间序列的随机项也可能会使得分析结果具有较大的不确定性。为消除这种不确定性,首先以时间为协变量模拟降水和潜在蒸散发的长期变化趋势,将二者表示为:
(2)
(3)
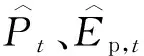
2.1.3 时变Budyko方程
单参数Budyko方程可表示为[20]
(4)
式中:E、P分别为实际蒸散发和降水量多年平均值(mm);φ=Ep/P,为干旱指数,Ep为潜在蒸散发量多年平均值(mm);w为流域特征参数;B(·)表示Budyko-type方程。
根据水量平衡原理,有
Q=P-E-ΔS。
(5)
式中:Q为多年平均径流深(mm);ΔS为流域蓄水变化量,在较长时间尺度上可忽略不计。将式(4)代入式(5)可得
Q=P[1-B(φ,w)] 。
(6)
为了捕捉各因素在年尺度上对径流的影响,可对w进行协变量分析,前人的研究常选择气温、降水、GDP、人口、灌溉面积等作为解释变量[12,17,20],但这种方法计算复杂,而且对数据要求很高,当研究区较小时(如滹沱河上游流域),很难获取高精度、长系列的GDP、灌溉面积等数据。因此,引入时序t作为方程参数w的解释变量,并且考虑线性和二次多项式2种形式,从而得到时变方程为:
Rt=Pt[1-B(φt,wt)] ;
(7)
wt=β0+β1t;
(8)
wt=β0+β1t+β2t2。
(9)
式中:Rt为基于时变Budyko方程所估计的第t年的径流深(mm);时序t=1,2,…;β0、β1、β2为方程参数,采用极大似然法估计。通过Budyko方程参数的协变量分析,既可以描述流域特征的时间变化,也可以基于Budyko假设实现年径流的模拟。单参数Budyko方程形式多样,其中,Choudhury-Yang方程形式简单、应用广泛[23-24],本研究基于Choudhury-Yang方程开展后续研究,其表达式为
(10)
将式(10)代入式(7)可得
(11)
当式(11)中的wt关于时序t的函数形式为常数、线性、二次多项式时,分别对应于常参数Budyko方程、线性Budyko方程、二次多项式Budyko方程。
2.1.4 基于分解法的径流影响分离
分解法的基本原理参见文献[11]、文献[12]、文献[21]。在年尺度上,干旱指数和流域特征对径流的年际影响量分别为:
(12)
(13)
式中Δa,t、Δo,t分别为从第t-1到第t年干旱指数和流域特征对年径流的年际影响量。由此可知,干旱指数、流域特征从开始年份t0到第t年对年径流的累积影响量分别为:
(14)
(15)
式中Aa,t、Ao,t分别为从初始年份t0到第t年干旱指数和流域特征对年径流的累积影响量。
2.1.5 多年尺度上干旱指数和流域特征对径流的影响
前人的研究大多在多年尺度上(即基准期和变化期)分离径流变化,为便于比较,本文在年尺度的基础上推导多年尺度干旱指数和流域特征对径流的影响。设研究时域的初、末年份分别为t0、t2,年径流系列的突变点为t1。那么,第t年的年径流Rt可表达为初始年份年径流Rt0与累积影响量的和,即
Rt=Rt0+Aa,t+Ao,t。
(16)
基准期(即t0~t1)的平均年径流Rpre、变化期(即t1+1~t2)的平均年径流Rpost表达如下:
(17)
同理,
(18)
基准期到变化期的径流变化量为
Rdiff=Rpost-Rpre=
(19)
式(19)右侧的第1项、第2项分别为从基准期到变化期干旱指数和流域特征对径流的影响量。
2.1.6 其他方法
采用Sen斜率法[25-26]及Mann-Kendall趋势检验法[27]估计水文气象系列的趋势及其显著性;同时采用滑动t检验、Mann-Kendall突变检验[28]对水文气象系列进行突变检测以提高结果的可靠性,通过2种方法检验(显著性水平均为0.05)的突变点才可判定为显著的突变点[29]。
2.2 研究区概况与数据来源
滹沱河全长587 km,是海河水系子牙河的主要支流之一,其上游的小觉水文站控制面积超过14 000 km2,是其主要控制站。滹沱河上游有云中河、牧马河、阳武河等众多支流,是岗南水库的主要产水区。岗南水库总库容为17.04亿m3,以防洪为主,兼有供水、灌溉等功能。滹沱河上游流域多年平均降水量为471.3 mm,多年平均气温为8.2 ℃,具有超过70%的植被覆盖度,属温带季风气候[30]。
本文所用主要数据包括:①小觉水文站1961—2016年逐月径流数据,摘录于水文年鉴;②五台山、原平、五寨、太原这4个国家基本气象站1961—2016年逐日气象数据,包括气温、降水、风速、相对湿度等,数据来自中国气象数据网,气象站分布如图1所示。
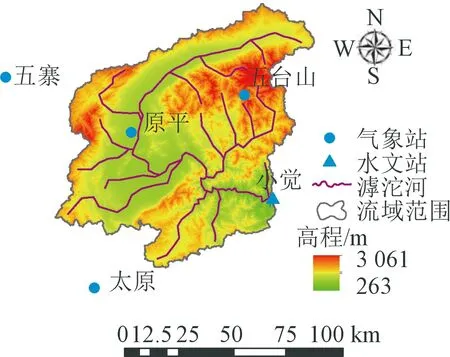
图1 滹沱河上游流域概况Fig.1 Topography,river networks,and meteorological stations in the upper reaches of Hutuo River basin
3 结果与分析
3.1 水文气象要素的时间变化趋势及拟合
经11 a滑动平均处理之后的水文气象要素序列的Sen趋势检验结果如图2所示:降水、年径流深都呈显著(P<0.001)下降趋势,潜在蒸散发与干旱指数则呈显著(P<0.001)上升趋势。经M-K与滑动t突变检测,四者均未发生突变。但原始年径流序列在1981年发生突变,限于篇幅,原始水文气象序列的趋势及突变检测结果省略。

图2 滹沱河上游流域水文气象要素变化趋势Fig.2 Trends of hydrology and meteorology elements in the upper reaches of Hutuo River basin
考虑线性和二次多项式2种函数形式对降水和潜在蒸散发的长期变化趋势进行模拟,并计算了贝叶斯信息准则BIC、均方根误差RMSE和Nash-Sutcliffe模型效率系数NSE[31]3个指标,结果如表1所示。由此可见,降水、潜在蒸散发的二次多项式模型的BIC、RMSE、NSE 3个指标均明显优于线性模型,因此,本研究将采用二次多项式模拟降水和潜在蒸散发的长期变化趋势。
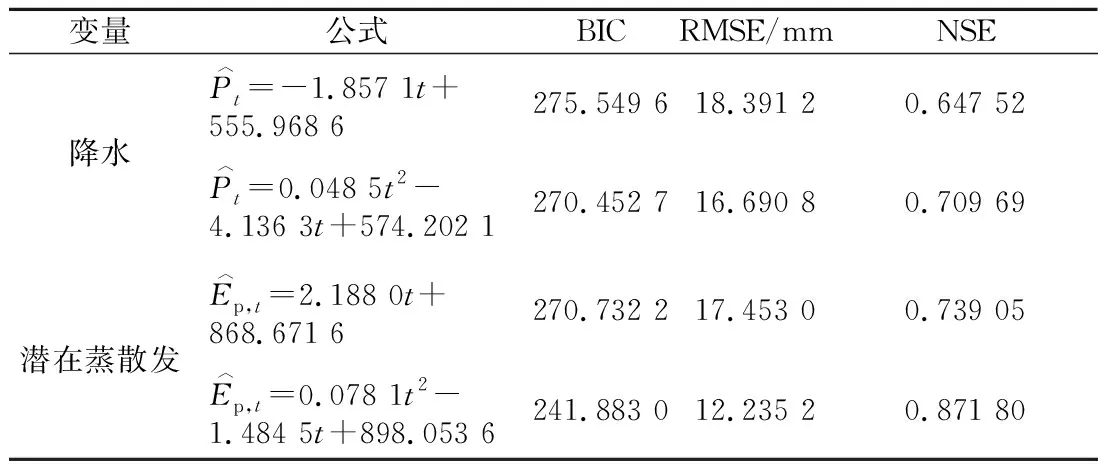
表1 气候因子的协变量分析结果Table 1 Results of covariate analysis of precipitation and potential evapotranspiration
3.2 时变Budyko模型的有效性
常参数(包括进行、不进行滑动平均处理2种情况)、线性、二次多项式4种Budyko方程的评价结果如表2所示。若未对原始水文气象数据进行滑动处理,常参数Budyko模型(即表2中的“常参数A”)的RMSE高达22.039 6 mm,NSE仅为0.416 83,说明不能进行有效的年径流模拟,主要原因可能是在年尺度上流域蓄水变量不为0。而在进行11 a滑动平均处理之后,常参数Budyko模型(即表2中的“常参数B”)的RMSE降低为6.708 1 mm,NSE提升到将近0.748 46,具有较好的年径流模拟能力,说明将时间序列进行滑动平均处理是必要的。时变Budyko模型较之常参数Budyko模型表现更优异,BIC、RMSE大幅减少,NSE大幅提升,高达0.88以上,表明时变Budyko模型拥有很好的年径流模拟能力。2个时变Budyko模型相比,二次多项式模型略占优势,因此,本文以二次多项式Budyko方程进行后续计算。
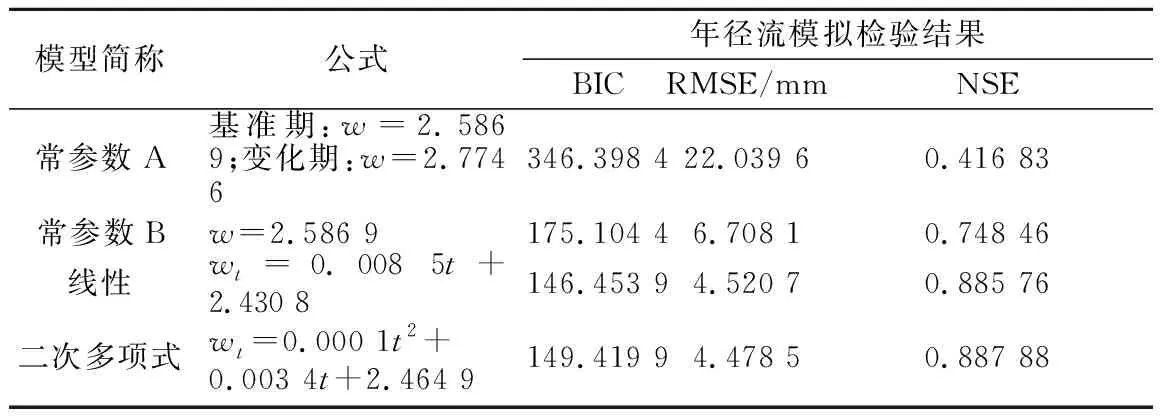
表2 Budyko方程参数w协变量分析结果Table 2 Results of covariate analysis of parameter w of the Budyko-type equation
3.3 与传统分段分解法的比较
因为原始观测径流在1981年发生突变,所以,以1981年为分割点划分基准期和变化期,基于常参数和时变Budyko模型进行2个时段间的径流变化分析,结果如表3所示。由表3可知:在对数据进行滑动平均处理的情况下,无论是径流影响量还是各因素的贡献率,二次多项式Budyko模型与常参数B模型的结果都很接近;若不进行滑动平均处理,常参数A模型所得的径流减少量大于二次多项式Budyko模型,原因可能是二次多项式Budyko模型在某种程度上消除了径流系列的周期性波动和随机性成分,使得径流的年际变化趋于平缓,尽管2种模型的贡献率也有一定差异,但二者均显示径流减少的主要因素是干旱指数。以上对比分析表明,本文构建的时变Budyko模型是可靠的。
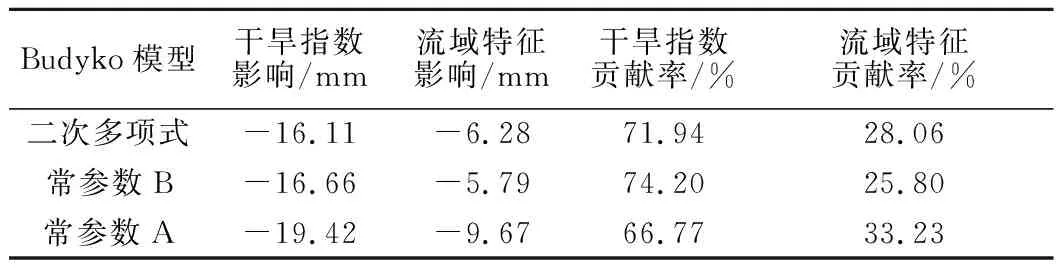
表3 从基准期到变化期的径流影响分离Table 3 Separation of annual runoff variation from prechange period to postchange period
3.4 滹沱河上游流域径流变化归因分析
基于二次多项式Budyko模型的年径流变化归因分析的结果如图3所示。由图3(a)可知,干旱指数和流域特征均导致年径流持续递减,至2011年,干旱指数和流域特征分别使得年径流累积减少29.74 mm和12.14 mm。由图3(a)曲线斜率变化可知:干旱指数对径流的影响强度(即年际影响量的绝对值,mm/a,下同)逐年降低,而流域特征在20世纪90年代之前对径流影响强度有较明显的增大趋势,之后基本保持稳定。从贡献率(图3(b))的角度来说,干旱指数和流域特征对滹沱河上游流域年径流减少的相对影响是一个此消彼长的过程,其中,干旱指数的贡献率由86.79%持续降低至71.01%,而流域特征的贡献率由13.21% 增加至28.09%,但是,滹沱河上游流域径流减少的主导因素始终是干旱指数。
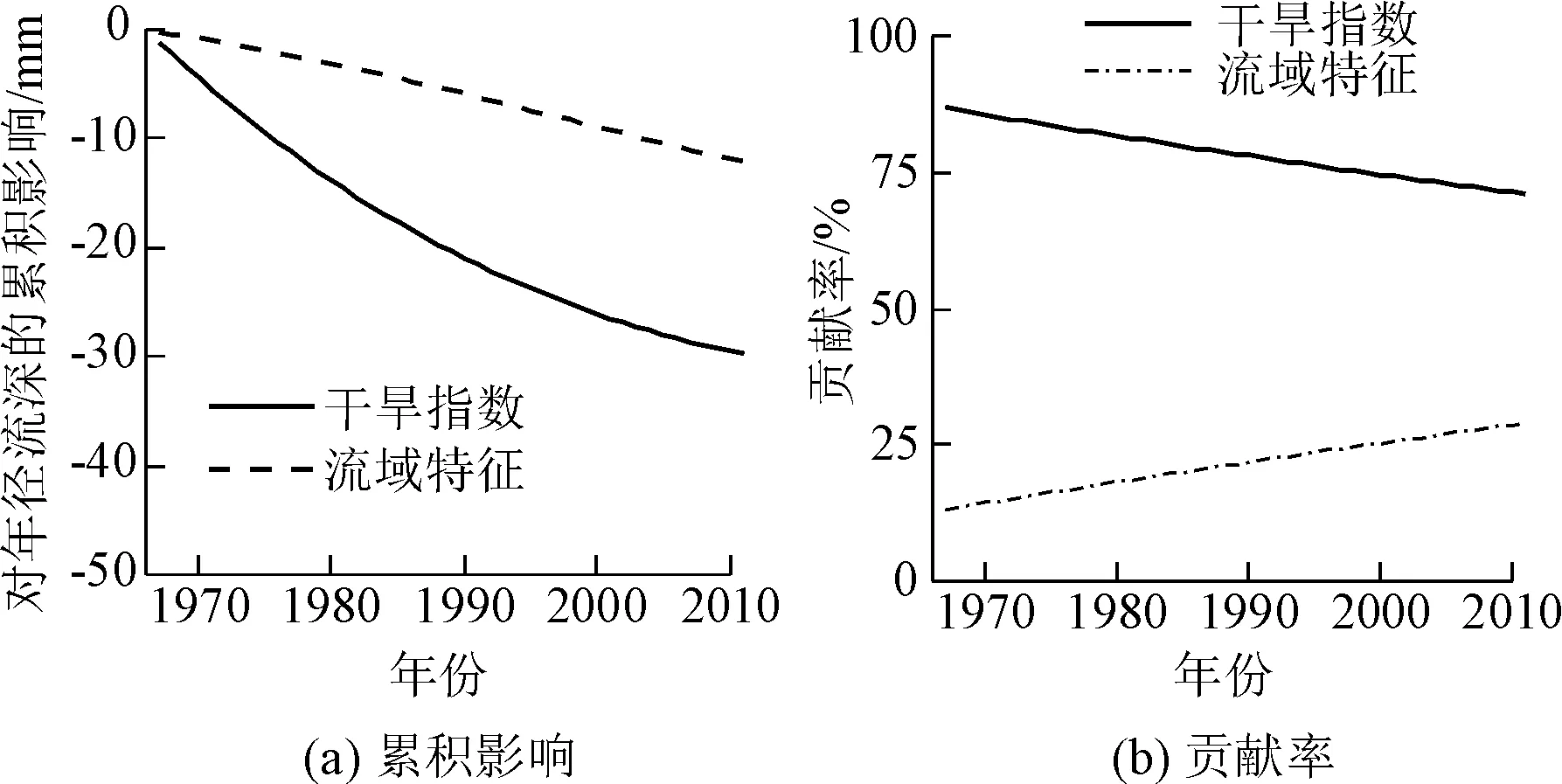
图3 基于二次多项式Budyko模型的径流影响分离Fig.3 Separation of the cumulative impacts of aridity index and catchment properties on runoff by the quadratic time-varying Budyko-type equation
但值得注意的是:图3(b)显示的流域特征对径流变化的贡献率越来越高,并非是反映了流域特征对径流影响的强度持续增加,更没有反映人类活动对滹沱河上游流域水循环的干预日益增强。实际上,从图4可以看出,流域特征对年径流的影响强度的变化相对较小,只在20世纪90年代之前有过一定幅度的增加,在20世纪90年代之后基本保持稳定,2000年之后甚至呈现减弱趋势,反观干旱指数,其对年径流的影响强度在整个研究时域持续减小,且减幅非常明显,换言之,图3(b)所显示的流域特征对径流变化贡献率的增加,主要是因为干旱指数对年径流的影响强度持续、明显减弱所致,尤其是在20世纪90年代之后。这与现实情况相符,在20世纪90年代之前,经济的快速增长所导致的下垫面变化(比如土地利用变化)、水工程建设等均对水循环的干预有所增强,表现为图4所示的20世纪90年代之前流域特征对年径流的影响强度增加;而在20世纪90年代之后,尤其是进入21世纪之后,在可持续发展、人与自然和谐相处等理念的影响之下,人们越来越重视水资源的可持续利用,相继采取了退耕还林、退耕还湖等一系列措施,因此,尽管城镇化建设、灌区建设等一系列因素还在影响水循环,但是年径流的减小程度应是受到了一定程度的遏制,正如图4所示;2000年之后,流域特征对年径流的影响强度在基本保持稳定的同时还有所减弱(计算结果显示,流域特征对年径流的影响强度在1999年达到最大,值为0.302 mm,此后呈小幅减少趋势,至2011年减小至0.291 mm)。这种年际尺度的变化环境下的水文效应,是基于常参数Budyko方程的传统分解法或敏感性方法所不能揭示的。
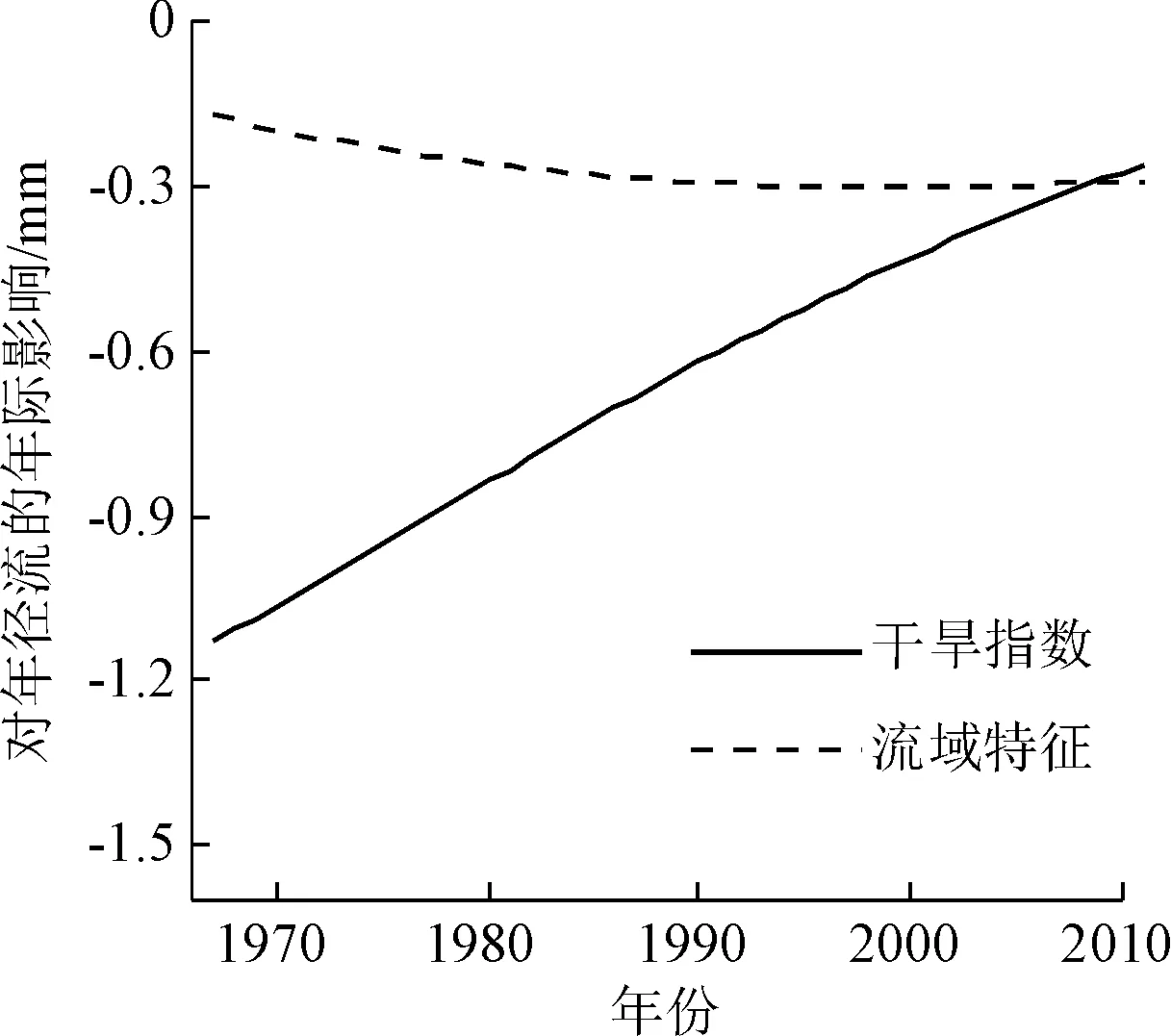
图4 基于二次多项式的Budyko方程的年径流年际影响分离Fig.4 Separation of the annual impacts of aridity index and catchment properties on runoff by the quadratic time-varying Budyko-type equation
4 讨论与结论
4.1 讨 论
4.1.1 时变Budyko模型的优点
本研究基于Wang和Hejazi[11]于2011年提出的分解法构建了一种年径流变化归因分析的新方法,与传统的基于单参数Budyko方程的分解法或者敏感性系数法相比,新方法的优点在于:
(1)对Budyko方程参数w进行了协变量分析,从而可以描述流域特征的时间变化,而传统方法假定在某固定时段内(如变化期或者基准期)流域特征保持不变,这与现实不符。
(2)基于w的协变量分析所构建的时变Budyko方程,可以在年尺度上分离干旱指数和流域特征对径流的影响,这可以帮助我们更深入地理解变化环境下的水文响应。
(3)时变Budyko方程较之常参数方程拥有更强的年径流模拟能力。
4.1.2 模型的改进
由于资料限制,本研究仅以时间为协变量构建了时变Budyko模型,虽然这种做法在不少研究中均有采用,但其缺乏物理基础,其稳定性和可靠性有待进一步验证,因此,在资料允许的情况下,建议选择具有实际物理意义的解释变量。此外,仅以时间为协变量,仍然无法在Budyko方程参数中分离人类活动和气候变化对径流的影响,这使得我们无法精确分离气候变化和人类活动的水文效应。因此限制了结果的适用性,如果分别选择代表气候变化和人类活动的两类变量为解释变量,如用北大西洋涛动NAO、太平洋年代际振荡IPO、大西洋多年代际振荡AMO等大尺度气候因子反映气候变化,而用GDP、人口、耕地面积、土地利用等因子反映人类活动,由此对w进行协变量分析,即可从中分离气候变化和人类活动对径流的影响,这不仅使得结果的可解释性更强,而且其实际意义也会更加明显。
4.2 结 论
本研究基于Budyko方程参数w的协变量分析,构建了时变Budyko模型,进一步改进了分解法,实现了在年尺度上分离干旱指数和流域特征对径流的影响。将该方法应用于滹沱河上游流域,所得的主要结论如下:
(1)时变Budyko模型的NSE远高于传统常参数模型,因此时变Budyko模型大大提高了年径流的模拟能力。基于线性方程的时变Budyko模型具有和二次多项式Budyko模型相似的结果。
(2)基于时变Budyko模型的分段研究的结果与传统常参数Budyko模型的结果相近,一定程度上说明了本文所提出的方法是可靠的。
(3)干旱指数和流域特征均导致滹沱河上游流域年径流减少,其中,干旱指数的贡献率由86.79%持续递减到71.01%,而流域特征的贡献率由13.21%持续增加至28.09%,因此,滹沱河上游流域径流减少的主导因素是干旱指数。
(4)干旱指数对年径流的影响强度逐年降低,而流域特征的影响强度相对稳定,因此,流域特征对年径流变化贡献率的增加,主要是干旱指数对年径流的影响强度明显减弱所致。

