视距约束下高架快速路圆曲线最小半径计算方法及应用

董 猛

[上海市政工程设计研究总院（集团）有限公司，上海市200092]

0 引 言

视距是公路与城市道路设计中的一项重要技术指标，是车辆正常行驶中，驾驶员从正常驾驶位置能够连续看到前方行车道范围内路面上一定高度障碍物，或者看到前方交通设施、路面标线的最远距离。现行《城市道路交通工程项目规范》（GB 55011—2021）[1]和《公路工程技术标准》（JTG B01—2014）[2]均对视距做了强制性要求。

目前，《公路路线设计规范》（JTG D20—2017）[3]和《城市道路路线设计规范》（CJJ 193—2012）[4]、《城市快速路设计规程》（CJJ 129—2009）[5]中圆曲线半径的最小值是根据车辆行驶的动力模型计算的，并没有考虑停车视距的要求。在具体工程设计实践中，根据规范要求的圆曲线最小半径设计的高等级道路，尤其是高架快速路，存在行车视线受中央分隔墩（及防眩设施）和两侧防撞护栏（及声屏障）影响而不满足停车视距的情况，容易引发安全隐患。

本文以高架快速路为例，根据规范要求的停车视距和横断面确定的横净距，通过简化计算模型计算最小圆曲线半径，并提出圆曲线最小半径建议值，供设计人员参考。

1 相关概念及术语

为统一概念术语，结合国内外规范和文献，对下列概念、术语及符号进行约定。

1.1 停车视距

停车视距是指车辆以一定速度行驶中，驾驶员自看到行车道前方障碍物时起，至到达障碍物前安全停车止所需要的最短行驶距离。本文中S 表示停车视距，是沿车道中心线的长度，如图1 所示。不同设计速度要求的停车视距见表1。

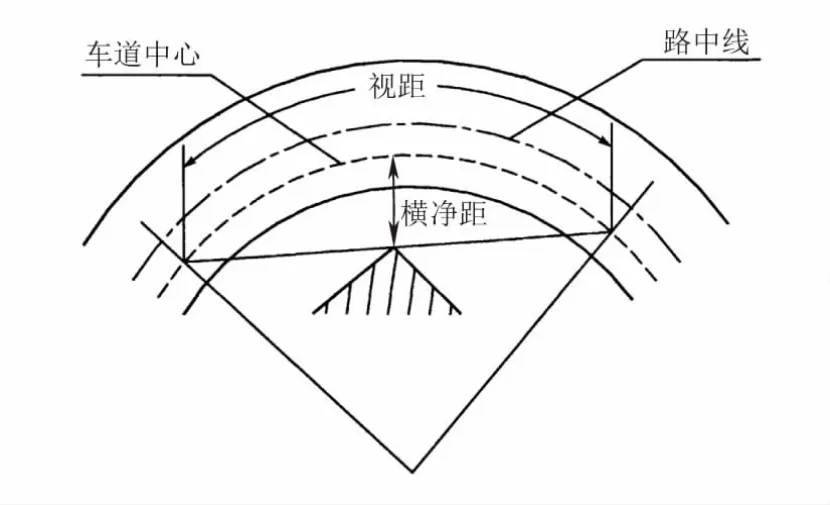
图1 视距、横净距示意图[6]

表1 不同设计速度对应的停车视距

小客车停车视距采用的驾驶员视点高度为1.2 m，视点前方路面上的障碍物顶点高度为0.10 m。

1.2 横净距

横净距是指在曲线路段内侧车道上的汽车驾驶员，看到行车道前方视距长度的视线与车道中心线之间的偏移值，是保证视距而必需的横向净空范围,在该范围内的一切障碍物都应加以避免或清除，如图1所示。本文中，h 表示横净距。

2 现行规范要求的圆曲线最小半径及视距验算

2.1 圆曲线最小半径

现行规范中圆曲线最小半径是以保证汽车在曲线上安全、舒适地行驶为条件确定的。圆曲线最小半径的实质是汽车行驶在曲线部分时，所产生的离心力等横向力不超过轮胎与路面的摩擦力所允许的界限。

根据车辆在弯道上行驶时的受力状况及各种力的几何关系，圆曲线最小半径按公式（1）计算确定，规范要求的快速路圆曲线最小半径见表2。

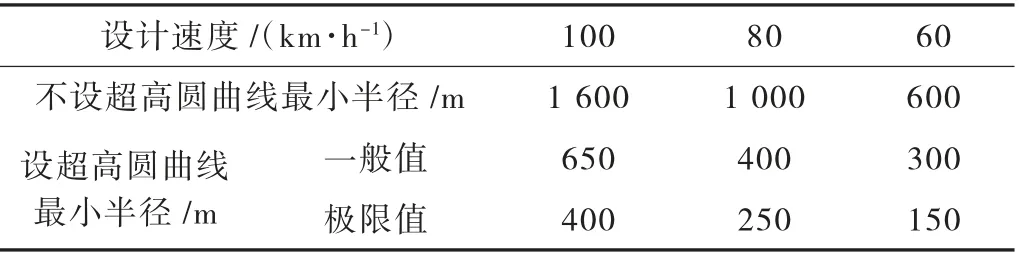
表2 快速路圆曲线最小半径

式中：R 为圆曲线最小半径，m；V 为设计速度，km/h；μ 为横向力系数，取轮与路面间的横向摩阻系数；i 为路面横坡度或超高横坡度。

2.2 视距验算

现行规范中要求平曲线内侧的路堑边坡、挡墙、绿化、声屏障、防眩设施等构筑物或建筑物均不得妨碍视线，对平曲线可能影响行车视距路段，应进行视距验算。

2.2.1 视距验算方法

视距验算通常采用横净距解析法和视距包络图法。鉴于城市快速路圆曲线长度通常大于相应的停车视距，本文中横净距解析法仅介绍停车视距小于圆曲线长度的情况。

（1）横净距解析法

如图2 所示，行车道中心圆曲线半径r=OA=OB，停车视距，横净距h=BC。

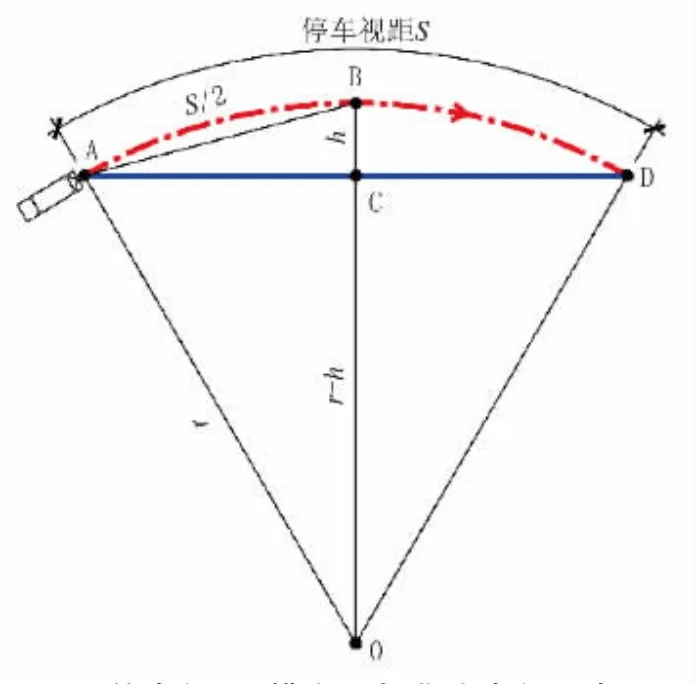
图2 停车视距、横净距与曲线半径示意图

在扇形AOB 中：

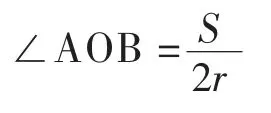
在RTΔAOC 中：

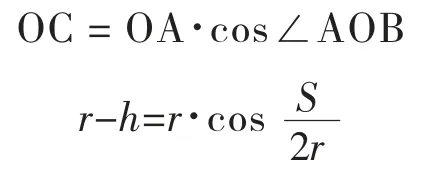
化简可得横净距h 的解析公式：

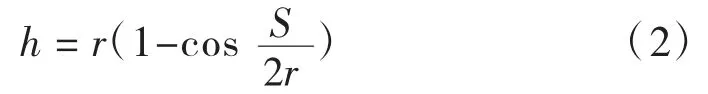
式中：h 为横净距，m；r 为行车道中心圆曲线半径，m；S 为停车视距，m。

（2）视距包络图法

横净距解析法计算只能通过试算倒推半径值，对于含有缓和曲线的平曲线视距验算尤为复杂。具体设计中可在平面图上用图解法画出视距曲线图，采用视距包络线作为平曲线视距的界限，判断圆曲线路段是否满足视距要求，如图3 所示。视距包络范围内的障碍物应予以清楚。

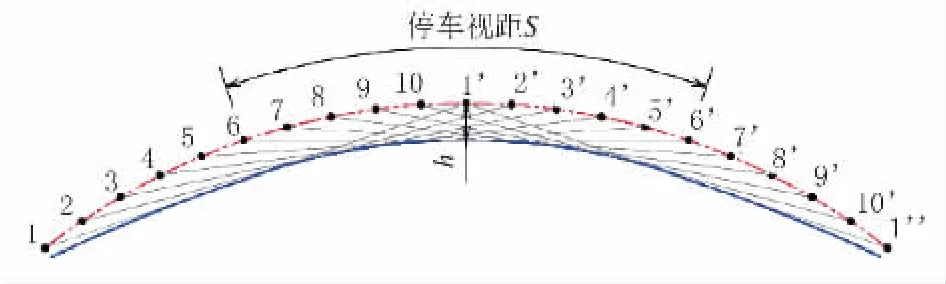
图3 视距包络图

2.2.2 圆曲线最小半径视距验算

目前，国内高架快速路普遍采用双向六车道规模，根据现行规范要求设置防撞设施及侧向宽度后，高架桥总宽一般为25.6 m。

如图4 所示，内侧车道宽3.5 m，内侧车道中心线r1距设计中心线的偏距为2.675 m，标准段横净距h1=2.5 m；外侧车道宽3.75 m，外侧车道中心线距设计中心线的偏距为9.8 m，标准段横净距h2=2.625 m。路缘带宽0.5 m，中央分隔护栏宽0.6 m，两侧防撞护栏宽0.5 m。

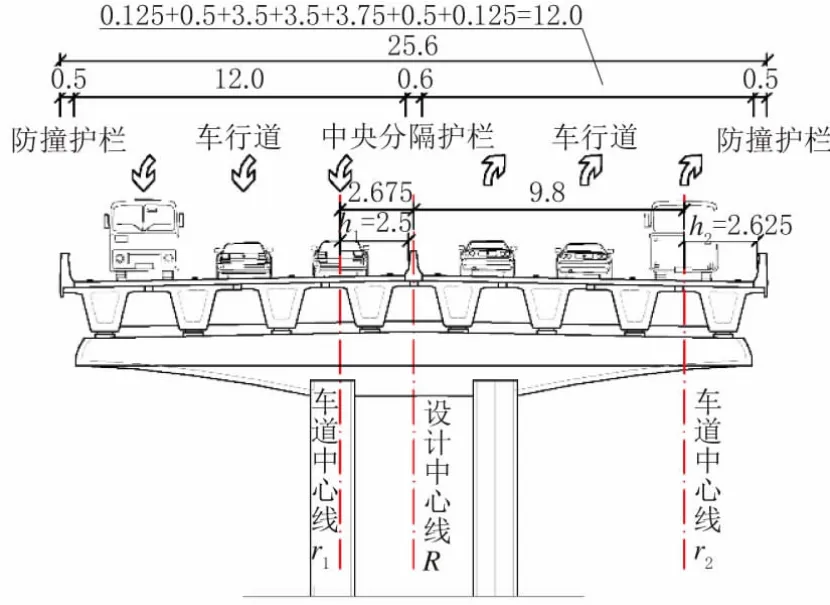
图4 高架快速路标准横断面示意图（单位：m）

根据《城市道路交通安全设施设计规范（2019版）》（GB 50688—2011），城市高架快速路设计速度100 km/h 或80 km/h 时，防撞护栏的防护等级为SS和SSm 级，护栏高1.1 m；设计速度60 km/h 时，防护等级为SA 和SAm 级，护栏高1.0 m。高架防撞护栏本身及附着在其上的设施杆件、防眩板和声屏障等都是遮挡视线的障碍物，需分别对内侧车道（受中央分隔护栏影响）及外侧车道（受边侧防撞护栏影响）验算横净距，如图5 所示。

图5 高架快速路平面示意图

本文采用横净距解析法（公式（2）），对不同设计速度的高架快速路采用设超高圆曲线最小半径一般值或极限值时，分别计算最小横净距，进行视距验算，计算结果见表3、表4。

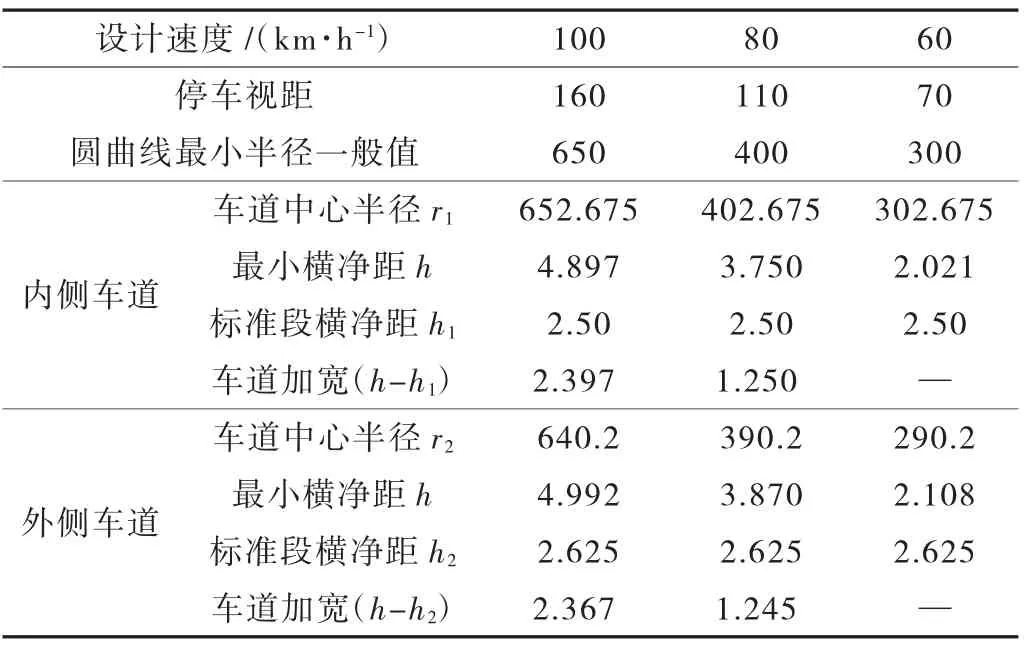
表3 设超高圆曲线最小半径（一般值）横净距及车道加宽计算 单位：m

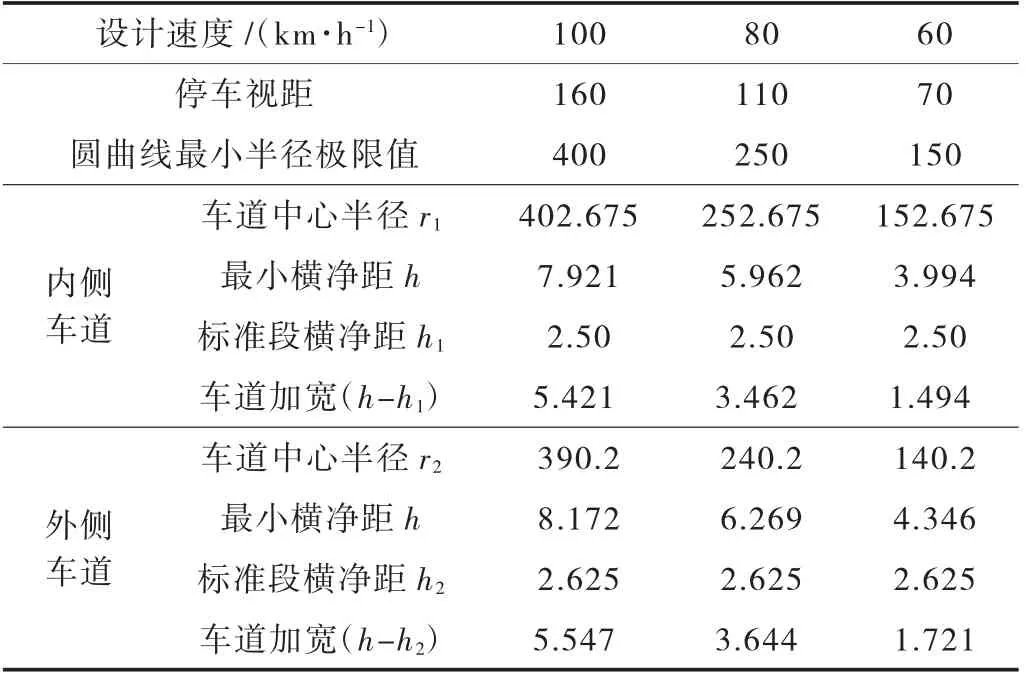
表4 设超高圆曲线最小半径（极限值）横净距及车道加宽计算 单位：m

从表3、表4 中可以看出：

（1）高架快速路只有在设计速度60 km/h，且采用圆曲线最小半径一般值300 m 时，按标准横断面布置的平面线形满足停车视距要求，不需对内外侧车道加宽；

（2）其余情况下，采用圆曲线最小半径一般值或极限值时，按标准横断面布置的平面线形存在行车视线受中央分隔墩（及防眩设施）和两侧防撞护栏（及声屏障）影响而不满足停车视距的情况，需对圆曲线范围的内外侧车道加宽，以满足视距要求的最小横净距；

（3）外侧车道在行车方向的右侧加宽，不影响行车轨迹；内侧车道的加宽是在行车方向的左侧，车道最大偏移5.5 m，道路线形与实际行车轨迹不符，不利于行车安全。

3 视距约束的圆曲线最小半径简化模型

现行规范要求的圆曲线最小半径及视距验算方法不能直接反应圆曲线半径与视距的关系。在实践过程中，需先按平面设计的圆曲线计算横净距值或画视距包络线，验算视距是否满足要求。如不满足视距要求，需返回调整平面设计。

本文针对高架快速路设计过程中容易忽视的视距问题，通过简化横净距解析法模型，推导出基于停车视距及横净距的圆曲线半径计算公式及最小圆曲线半径的建议值，便于设计人员灵活运用。

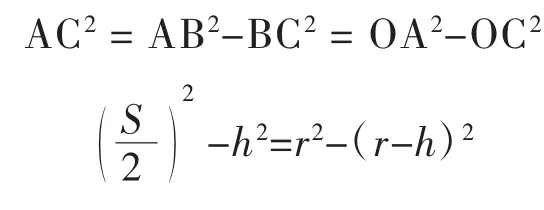
化简可得：

式中：r 为行车道中心圆曲线半径，m；S 为停车视距，m；h 为横净距，m。

简化模型中线段AB 的实际长度小于停车视距S 的一半（即S/2），按S/2 取值计算的r 值略大，有利于控制设计指标，满足最小圆曲线半径控制要求。

4 视距约束下圆曲线最小半径计算及应用

根据图4、图5 确定的设计参数，按照简化模型公式（3），分别对内侧车道（受中央分隔护栏影响）及外侧车道（受边侧防撞护栏影响）计算满足停车视距要求的最小圆曲线半径。

4.1 视距约束条件下内侧车道及设计中心线最小半径计算

如图4 和图5 所示，内侧车道中心线r1距设计中心线的偏距为2.675 m，横净距h1=2.5 m，根据公式（3）计算得视距约束条件下内侧车道及设计中心线最小半径见表5。

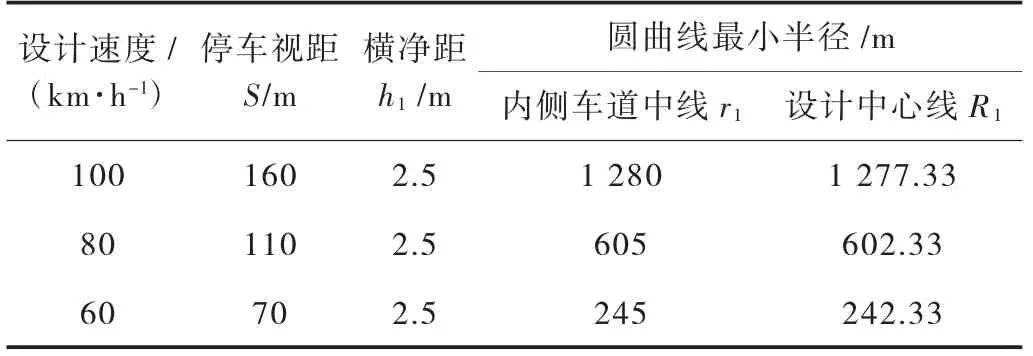
表5 视距约束条件下内侧车道及设计中心线最小半径

内侧车道中心圆曲线最小半径：

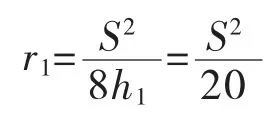
设计中心线处圆曲线最小半径：

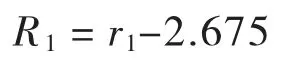
4.2 视距约束条件下外侧车道及设计中心线最小半径计算

如图4、图5 所示，外侧车道中心线距设计中心线的偏距为9.8 m，横净距h2=2.625 m，根据公式（3）算得视距约束条件下外侧车道及设计中心线最小半径见表6。

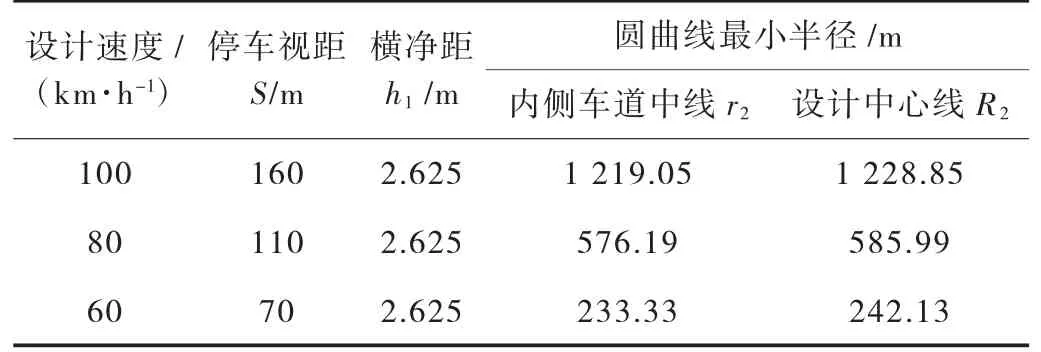
表6 视距约束条件下外侧车道及设计中心线最小半径

外侧车道中心圆曲线最小半径：

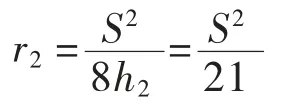
设计中心线处圆曲线最小半径：

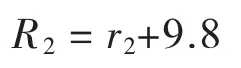
4.3 视距约束下双向六车道高架快速路圆曲线最小半径建议值

从表5、表6 的计算结果可以看出，中央分隔护栏和两侧防撞护栏对高架快速路的视距都有明显的影响，规范规定的设超高圆曲线最小半径不能满足高架快速路的视距要求。

设计速度60 km/h 时，中央分隔护栏与边侧防撞护栏对视距的影响大致相当；设计速度80 km/h或100 km/h 时，中央分隔护栏对视距的影响更大。设计中心线的圆曲线最小半径R 应取大值，即R=max{R1，R2}。

综上所述，双向六车道高架快速路圆曲线最小半径建议值见表7。

表7 双向六车道高架快速路圆曲线最小半径建议值

5 结 语

本文通过高架快速路圆曲线行车视距的研究，力求从视距安全的角度为圆曲线最小半径提供一种简化计算方法，以弥补过往凭工程经验进行设计的不足，计算结论可供相关工程技术人员参考。

本文介绍的计算方法具有普适性，不仅适用于双向六车道高架快速路，也适用于行车道两侧有障碍物情况下确定满足停车视距要求的圆曲线半径。