递推法在C语言项目实践中的应用技巧

唐小健

(广东省韶关市中等职业技术学校，广东 韶关 512000)

0 引言

所谓递推法就是给定某个初始值，或称为旧值，归纳出新值和旧值之间的内在联系，如此不停地一直运算下去，直到得出需要的数值。这里需要知道的是新值的求出要看旧值的求出，如果旧值无法求出，那么新值也就无法推导出来。这跟数学上的递推公式是同一类问题。

从以上对递推法的阐述，要使用递推法进行求解问题，关键是在确定初始值的基础上，如何找出新值和旧值之间的内在联系即运算规律是关键，规律找出来了，就可以顺利的进行递推，得到解题结果就是时间问题了。所以说，只要找出其中的数的运算规律，可以说项目实践成功了一大半。下面在详述项目的解题过程中，着重对数据之间的关系以及递推的具体实现进行分析和探究。

1 项目实践1：递推法解决斐波那契数列问题

1.1 项目任务

打印输出斐波那契数列的前40 项。斐波那契数列的前几项是：1，1，2，3，5，8，13，21，34，…。输出格式是每行输出4个数。

1.2 项目分析

初看斐波那契数列的前几项，相邻的数之间或前后数之间好像没有任何内在的关系，第一项是1，第二项还是1，第三项是2，第四项是3，第五项是5，……。可是只要仔细分析，其数据之间的内在联系即规律也就一目了然了，原来，斐波那契数列的分布规律是：从第三项开始，每个数等于前面两个数之和。

对于这个“简单”的问题，在C 语言编程教学中需要用递推法来实现，下面详述了这个问题。

用变量a，b 和c 来描述递推过程，可以把这三个变量当做会移动的指针或者游标。现在把数列的第一项数值1 赋值给变量a，把数列的第二项数值1 赋值给变量b。此时变量a 指向第一个数1，变量b 指向第二个数1。把前面两个数相加的结果赋值给变量c，即c=a+b，此时变量c指向第三个数2，如图1所示。

图1 斐波那契数列的第1次运算分析图

上面只是得到第一个新值（第三个数2），那么，又如何得到第二个新值（第四个数3）呢？上面说到可以把变量当做指针来操作，如果把变量a，b 从左顺序向右移动一个位置，又进行c=a+b赋值操作，此时的变量c指向第四个数3，如图2所示。

图2 斐波那契数列的第2次运算分析图

按照这个规律顺序向右移动变量a和b一个位置，进行c=a+b 操作，变量c 也随之向右移动一个位置，变量c 代表的是递推出来的一个个的“新值”，如果进行输出，那问题不就得到解决了吗。

仔细观察上面的运算分析图可以很清晰的发现，变量a，b 及c 的递推承接关系，变量a，b、c 顺序指向相邻的三个数，不管怎么移动，移动几次，执行的都是c=a+b 操作，关键是变量a，b 及c 不是固定不变的，随着指向不同位置上的数值，变量的值也是随之改变的。分析上面的运算分析图可以很容易确定变量a，b 及c的递推承接关系：

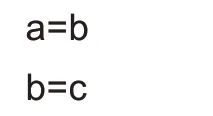
确定了变量的递推关系表达式，就可以动手编写具体的C程序代码了。

1.3 项目实践的C语言程序框架设计

可以先定义好基本类型整型变量a、b、c、t及count，变量a、b、c 用来指向斐波那契数列中的相邻的三个数，变量t 用来控制变量移动的次数。因为前两项预先已经输出，要求输出40项，因此只要从左向右顺序移动的次数是38次，也即变量t 的控制范围是[1，38]，用C 语言中的循环控制语句for 就可以实现。变量count 是个计数器，用来统计数列中数的个数，控制每行输出四个数，赋初值为2（统计前两个数）。程序的总体框架可以设计如下：

1.4 项目实践的完整C语言程序如下

1.5 C程序的运行

运行上面的C 语言程序，可输出斐波那契数列的前40项，每行四个数，共有十行，如图3所示。

图3 按照4×10格式输出斐波那契数列前40项

1.6 项目算法设计的改进

毫无疑问，以上递推算法的设计可以顺利的求解斐波那契数列问题，循环递推了38次，从第三个数的单个输出开始，每个数就要循环递推一次。运算效率不是很高，那有没有可以提高解题效率的递推算法呢？答案显然是肯定的。

再仔细观察和分析上面的图1 图2 运算分析图，可知要递推出下一个“新数”，只要把变量a和b顺序向右移动一个位置。能不能每次顺序向右移动二个位置，同时输出两项呢？答案显然也是肯定的、可行的。具体见以下分析。

同样定义两个整型变量a和b，用来指向相邻的两个数，首先把第一项1 赋值给变量a，把第二项1 赋值给变量b，也即a=1，b=1。此时变量a 指向数列的第一项，变量b指向数列的第二项，如图4所示。

图4 斐波那契数列的改进分析①

把变量a 和b 同时向右移动二个位置，此时变量a指向第三个数2，变量b指向第四个数3，如图5所示。

图5 斐波那契数列的改进分析②

此时如果执行如下运算：

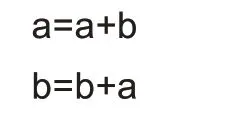
会得到a=a+b=1+1=2，b=b+a=1+2=3，我们惊奇地发现，a 和b 的指向跟图5 一样，a 指向第三个数2，b 指向第四个数3。

再把变量a和b同时向右移动二个位置，此时变量a指向第五个数5，变量b指向第六个数8，如图6所示。

图6 斐波那契数列的改进分析③

同样地，执行运算a=a+b 和b=b+a，此时a=2+3=5，b=3+5=8，a 指向第五个数5，b 指向第六个数8，指向跟图6一样。

到此为止，可以验证变量a和b每次同时向右移动二个位置，同时算出两个“新数”的改进递推算法是完全可行的。因为每次输出两项，所以循环控制次数总共只需要20 次就行了，大大提高了程序的运行效率。只要把上面的程序稍作修改就可以了，改进后的完整C程序如下所示。

需要注意的是该程序跟改进之前的程序是不完全一样的：①所有40 个数都是在进入循环之后输出的；②计数器变量count初始赋值为0；③for循环控制语句只需要循环20次，每次输出两个数；④递推的实现语句不一样：改进之前是“a=b;b=c;”，改进之后是“a=a+b;b=b+a;”。执行上面程序，输出结果是一样的。

1.7 项目实践的进阶：斐波那契数列的另类解法

如果对普通变量的动态赋值问题理解不是很透彻，可以考虑用C语言中的数组技术来求解。事实上，数组的应用在任何高级编程语言中都是极其重要的一项操作，可以解决许多用普通变量无法求解的复杂问题，编写程序更加简练，更加易于理解，方便程序的编译和调试，在代码二次修改方面也更加方便，C语言当然也不例外。

因为数组中的分量是带有下标的，正好可以用来存放具有某些规律的一系列数据，通过一定的算法运算可以快速的得到问题的答案。下面我们使用C语言中的数组和递推算法来进行斐波那契数列的前40 项输出，也是每行输出四个数。

程序首先定义好三个变量：因为输出的数据较大，所以需要定义一个放置数列各项数据的长整型数组变量shulie[40]，数组下标从0 开始，分量shulie[0]赋初值为斐波那契数列的第一项数据1，分量shulie[1]赋初值为斐波那契数列的第二项数据1；循环控制变量i，为普通整数类型；计数器变量count，为普通整数类型，赋初值为2。在进入循环之前先输出数组的前两项，进入循环之后判断计数器的数值是否是4 的整数倍，是的话就输出换行符号进行换行，否则按照递推规律进行新值的运算并输出，同时计数器进行自加1操作。因为数组的下标从0 开始的，现在要输出40 个数，所以循环控制变量i的遍历范围是[0,39]。

完整的C程序代码如下：

此程序采用数组实现了每次向右移动一个位置，每次输出一个数。如果要求每次向右移动二个位置，每次输出两个数，那么需要修改程序。如果我们对C 语言程序的执行流程理解透彻，就只需对上面程序稍加修改便可以达到这个目的。修改之后的C程序如下：

2 项目实践2：递推法解决猴子吃桃问题

2.1 项目任务

有只猴子在第一天摘下若干个桃子，马上吃了一半又多吃了一个；第二天早上将前一天吃剩下的桃子吃掉一半又多吃了一个；以后每天早上都吃了前一天吃剩下的一半零一个。到第10天早上想吃桃子时，此时只剩下一个桃子了。请用C语言编程求解猴子第一天一共摘下多少个桃子？

2.2 项目分析

这个问题比较简单，是个典型的迭代问题，可以使用递推算法求解。项目实践1的递推是头开始逐步推出后面的每一项数据的。本项目同样可以采用递推算法进行求解，只不过递推的顺序正好相反，从最后一项数据开始倒推，逐步推出前面的每一项数据。

前面说过，递推的关键是找出新值与旧值之间的关系。下面就来找出猴子吃桃问题的前后相邻两天的桃子数之间的关系。

假设前后相邻两天的桃子数定义为qian 和hou，那么根据倒推的递推算法，应用数学的思维，确定每天的桃子数。最后一天（第10 天）的桃子数为1 个的话，第九天的桃子数应该就是4个，…，一直推到第一天的桃子数，问题得到解决。如表1所示。

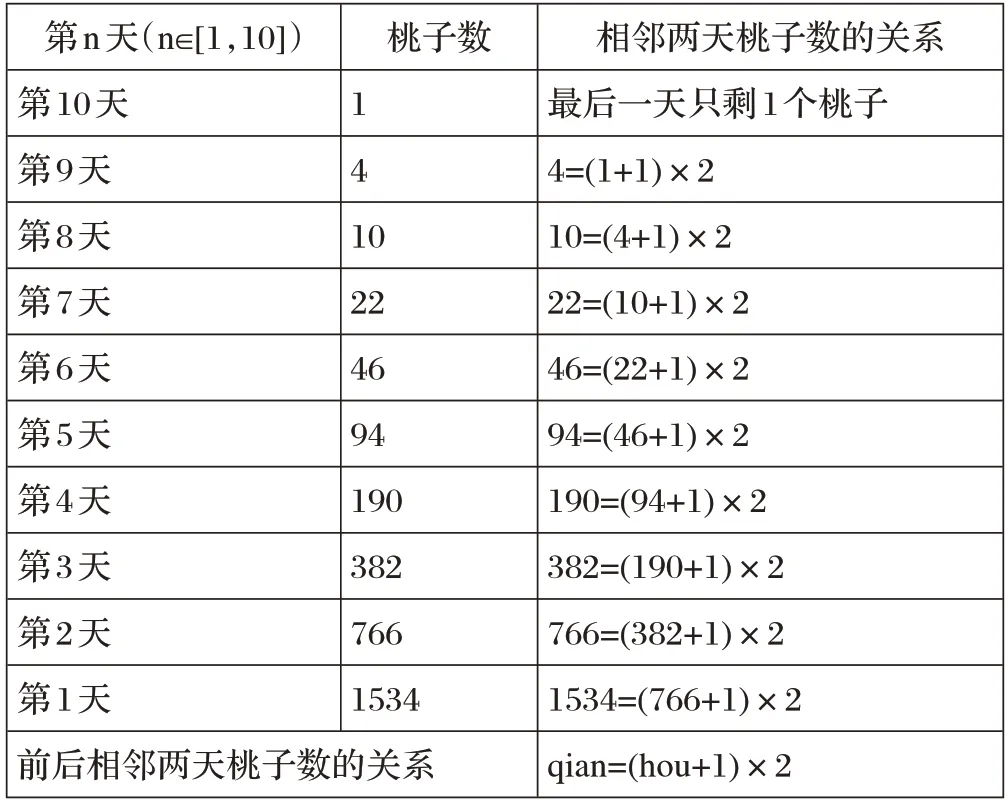
表1 猴子吃桃问题的项目分析表

通过上表的数据分析，确定前后相邻两天桃子数的关系是qian=(hou+1)×2。这里有两个变量qian 和hou，分别存放前后相邻两天桃子的数量，如果在使用变量hou递推出变量qian的数值之后，hou的值就不用保存了，因此这里可以只定义一个变量taozi，用来临时存放每天的桃子数量，那么前后相邻两天桃子数的关系是就可以表述为taozi=(taozi+1)*2。

2.3 项目实践的完整C语言程序

代码如下：

该程序的控制思路：①定义整型变量taozi 及n，taozi 用来统计每天的桃子数量，n 是循环控制变量；②采用倒推的递推算法，所以变量n 是从9 开始递减的，一直到第一天为止；③在循环体中循环执行递推关系表达式taozi=(taozi+1)*2，一直到计算出第一天的桃子数为止。

2.4 程序执行结果

猴子在第一天总共摘下1534个桃子。

2.5 项目实践的进阶

同样的，猴子吃桃问题也可以使用递推算法和数组技术进行求解，其完整的C程序如下。

3 结束语

本文研究了C语言编程教学中对于递推法的应用技巧，给出对斐波那契数列问题和猴子吃桃问题的求解。其实很多问题通过分析和算法设计，都可以归结到递推的算法上来，关键在于我们能不能够分析出问题中所蕴含的相邻数据之间的关系，因为这是顺利进行递推的前提和基础。善用递推算法可以拓宽C语言编程思维，进而提高使用C 语言程序设计解决实际应用问题的能力。