两类创新及其与经济增长的协同演化机理①
周 建, 周杨雯倩, 叶 梁
(上海财经大学经济学院, 上海 200433)
0 引 言
21世纪以来,科技创新已经成为世界各国提高综合国力的重要战略支撑和决定性因素,是社会和经济发展的关键[1].正因为如此,有关科技创新与经济增长的理论与政策研究引起了相关学者前所未有的关注.中国自改革开放以来经济发展取得了举世瞩目的成就,综合国力日益提升,但中国的科技创新能力总体还较薄弱,在世界上缺乏足够的竞争力和影响力,这也是不争的事实.近年来,我国处于经济增长动能转换的关键时期,创新是引领经济转型升级和持续发展的强大引擎,因此,科技创新作为提高社会生产和综合国力的战略支撑,必须摆在国家发展全局的核心位置.随着创新驱动发展战略的提出,未来经济增长动力必然从要素驱动向创新驱动转型,形成以创新为核心的全面推动经济持续健康发展的格局,这是实现经济高质量发展和未来现代化建设的重要保障.由此更加确定了创新对于中国经济发展引领和推动的重大作用和意义.
创新往往与研发活动紧密相联,研发活动是创新过程的基础和不可或缺的过程.我国研发活动的定义和分类与联合国教科文组织基本相同,包括基础研究、应用研究和试验发展.基于研发活动的内涵,根据其定义、含义和内在实质进行的分类得到了学术界认可,认为基础研究与应用研究均以创造知识为目的将其划分为一类,而区别于利用已有知识而进行的试验发展活动[2-6],据此本文将基础研究和应用研究划分为基础类创新,将试验发展活动划分为应用类创新.
已有传统文献认为,由于基础类创新的特性,决定了其在创新活动中只处于基础地位,不以经济效益为指标,是经济产出和发展的基石,是后续研发活动的根本保证和桥梁,对经济产出没有直接明显的效用.而应用类创新在基础类创新的基础上,将科研成果转化为可行的工艺或者新产品,形成巨大的经济效应,使社会产出增加,推进经济发展和社会进步,是直接产生作用的过程.总体来看,创新活动对经济增长的影响主要体现为从量变到质变的过程,随着知识的逐渐积累,知识技术逐渐被物化到物质资本和人力资本中,成为经济系统技术要素的一部分,形成社会知识积累和技术进步,从而促进了经济增长.随后由于溢出等效应演变为一场技术革命,进而引发社会的产业革命,进入新的循环.
现代科技创新活动复杂多变,并且对社会和经济发展十分重要,除了上述传统一般性观点的特征之外,还有两个十分重要的特性现有相关文献没有充分注意到:两类创新之间的反馈效应及其与经济增长的网络化传导机制.第一,如图1所示,事实上,基础类创新不仅单向影响应用类创新和经济增长,而且应用类创新也会反馈影响基础类创新,考察不同创新之间真实而客观的反馈效应弥补了已往文献只过度强调创新活动间单一传导途径的不足,从而使得创新理论更加符合现实.第二,基础类创新不仅通过应用类创新间接影响经济增长,而且也可能直接影响经济增长,这也是现有文献经常忽略的.由此可知,不同创新和经济增长之间呈现出协同演化机理,而非传统文献的单向直线型关联机制.
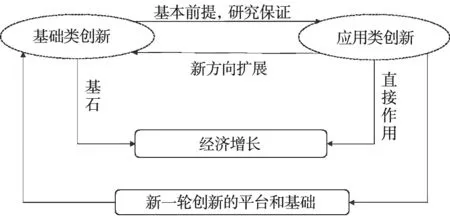
图1 两类创新及其与经济增长的协同演化机理Fig.1 Two types of innovation and their co-evolution mechanism with economic growth
关于不同创新活动及其与经济增长的内在反馈效应及网络化传导机制的现实案例,电子商务行业作为最直接的证据具有普遍的说服力.该行业最早产生于20世纪60年代,发展于90年代,其发展得益于这几十年间计算机科学、数学、控制理论、统计学、网络理论等众多领域的基础类创新的广泛应用,它们为电子商务的现实产业发展提供了重要的基础和前提保障.从这一发展过程可以看出,正是伴随着相关基础类创新领域知识技术的成熟才会出现近20年电商的蓬勃发展,同时,电商的快速发展对我国经济增长和发展的贡献和作用越来越大,由此反映出在创新活动中由基础类创新到应用类创新,进而促进经济发展传统的传导路径.与此同时,电子商务的发展导致人们的生活工作模式、思考方式、行为习惯等产生了根本性的变化,很大程度上改变了现有科学研究结构和产业结构.电子商务的突飞猛进发展,不仅使得现有科技创新能够不断融合电子商务的最新应用和实践成果,提升既有基础类创新的开发能力和水平,而且在很大程度上还促使和催生了新兴的大数据理论、人工智能、“互联网+”等各种新的基础类创新方向,这些新的创新方向对经济增长也存在着直接的重要作用.这直接反映了电子商务对基础类创新具有反馈效应,这一现象也更符合中国长期以来以消化吸收为主的创新模式,即通过新技术的引进催生和引发新的基础类创新方向,扩展创新的边界.综上表明,电子商务等应用类创新不仅是原有基础类创新的直接现实商业化和产业化成果,而且也是现有很多新的基础类创新的缘由和起点,基础类创新和应用类创新之间不是单向的直线传导途径,而是具有反馈效应的复杂传导途径.由此,两类创新活动之间及其与经济增长之间呈现出具有反馈效应的协同演化机理.
综合以上分析可知,现实中基础类创新、应用类创新与经济增长之间的影响关系并不像现有一般性文献所描述的由基础类创新影响应用类创新,进而影响经济增长的传导路径那样简单和直接,除此之外,还完全可能存在着应用类创新对基础类创新的反馈效应,以及基础类创新对经济增长的直接影响机制,由此形成两类创新之间的反馈效应,以及两类创新与经济增长之间的网络化传导机制.虽然文献中已有针对创新网络动态方面的研究,但是大多是针对产业内或产业间平行的创新构成的关系网络[1,7].正是这一被现有文献忽略,但现实中而不应该被忽略的重要特征构成了本文的研究动机.本文以标准的数理经济学和现代高级宏观经济学相关分析体系为基础,通过引入更为贴近中国现实的创新之间反馈效应及其与经济增长之间的网络化传导机制,较为严谨地对两类创新及其与经济增长的协同演化机理进行系统性分析.在理论研究基础上,进一步从实证的角度对两类创新及其经济增长的协同演化机理进行了计量检验,得到了具有政策启示意义和借鉴价值的重要结论.
在已有文献研究的基础上,本文的创新和学术贡献主要在以下3方面:第一,突破已有文献仅仅只考虑基础类创新单向影响应用类创新,而未能考虑到应用类创新对基础类创新的反馈机制的不足,引入反馈效应,创新性地设定和考虑了符合中国现实特征、具有双向复合结构功能的两类创新的传导路径,在现有多部门复杂经济系统中,通过较为严格的数理经济学理论推导、证明和分析了应用类创新和基础类创新之间的动态传导机制和循环反馈作用机理,并对相关理论性质进行了严格证明和经济学意义上的理论分析.第二,在生产函数中同时引入基础类创新和应用类创新,克服已有文献一般性只考虑基础类创新通过影响应用类创新,进而再影响经济产出的单向途径缺陷.在功能上不仅能够反映已有文献的创新作用于产出的单向途径,而且还能够拓展反映基础类创新直接作用于产出等其他多种途径,将已有文献中基础类创新到应用类创新再到产出之间的直线关联扩展到三者之间更加接近现实的协同演化的关联结构,深度刻画了其中的真实复杂机制.第三,在理论机制研究基础上,对两类创新的反馈效应及其与经济增长之间的网络化传导机制进行了实证检验,发现这些机制的真实存在性,这进一步为本文的理论分析和创新政策研究提供了新的科学证据和依据.
1 相关文献评价
在不同的创新分类方式下,关于不同类别创新的研究在现有文献中逐渐丰富,例如,从企业的角度而言,盛光华和张志远[8]从博弈论的角度分析了不同的政府补贴方式对企业渐进式和突破式创新模式选择的影响.张洁等[9]用纵向案例对比研究方法,以华为和IBM公司为代表,对比不同制度环境下领先企业不同时期的开放式双元创新活动形成的演进路径的相似性与差异性.杨晔等[10]从员工技能结构的视角研究了产品和工艺创新对中小企业雇佣需求的影响.从创新驱动因素的角度而言,周晶淼等[11]基于DICE模型,分析了导向性技术创新中不同的动力要素对经济体中相关变量的影响.上述相关研究均未考虑或在定量上分析不同创新之间的相互影响.
考虑到前文所述的两类创新的反馈效应,就本文的分类方式而言,在内生增长模型框架下,虽然关于科技创新与经济增长的文献种类繁多,但是就两类创新与经济增长机制的相关文献还在进一步探索.在理论上,国外研究方面,Akcigit等[12]在多行业的模型中将创新部门扩展为应用类创新和基础类创新两部门,但是并未考虑两者之间的反馈效应,仅设定了基础类创新对应用类创新在行业间和行业内的溢出效应,也未在模型中考虑到创新之间的溢出机制以及对创新结构的最优状态进行分析.但是正如引言中指出,这两类创新之间存在的交织反馈作用机制十分重要,忽略这一机制在理论和实证上会存在着明显不足.同时,Prettner和Werner[13]在内生增长模型中包含了基础类创新和应用类创新,并考虑了两者之间的溢出效应,内生化了生育率和教育,并且认为基础类创新对经济增长有促进作用,但两类创新的生产函数设定形式上没有差异,即两类创新在研发中有同质的作用.为了克服这一缺陷,本文在此方面进行了有价值的区分.Konishi[14]与Prettner和Werner[13]从福利的角度分析基础类创新对家庭福利的影响,发现基础类创新在稳态福利最大化时的水平低于其在稳态增长最大化时的水平;Gersbach等[15]也是将创新部门扩展为两类创新,考虑了双向溢出效应,但模型设定的基础在于应用类创新由基础类创新所得到的知识理论或思想前沿而来,并且受到基础类创新发展的限制.这些文献的研究都没有完全刻画和反映类似于中国这样的投资驱动阶段的消化吸收创新模式.在国内研究方面,基于半内生增长模型框架下,杨立岩和潘慧峰[2]在Jones[16]的模型下进行扩展,区分了基础类和应用类创新,其中基础类创新的产出由相应的人力资本投入决定,并且它决定着经济增长率,因此人力资本是经济增长的真正源泉,而且政府在促进经济增长中可以大有作为.与杨立岩和潘慧峰[2]不同的是,严成樑和龚六堂[3]中基础类创新的增长率不依赖于人口增长,他们在Jones[16]的框架下设定模型,假设基础类创新不能产生直接的经济效应,但是却是经济运行不可缺少的,同时应用类创新的生产效率取决于基础类创新存量,但反向关系并不成立.贺俊等[17]将严成樑和龚六堂[3]的研究扩展为开放经济,并从静态的角度对参数进行了分析.孙早和许薛璐[18]在类似的框架下针对应用类创新引入了技术前沿的概念,理论上分析了两类创新的作用机制.许治和周寄中[19]在AH模型下加入基础类创新的生产函数,阐述了基础类创新对经济增长的两种影响途径,通过比较静态分析发现基础类创新强度与其生产知识的弹性系数正相关,而应用类创新投入与基础类创新的弹性和“干中学”效率负相关.基于以上这些文献可以看出,目前国内理论相关文献区分了基础类创新和应用类创新,仅考虑了基础类创新对于应用类创新的单向影响,忽略了应用类创新对于基础类创新的反馈效应和基础类创新对于经济增长存在的直接效应;国外部分文献虽然考虑了双向溢出特征,但是它们并非是本文引言中所阐述的两类创新之间的反馈效应,这些研究与中国真实的现实情况之间可能存在着较大程度的偏离.因此,在理论上十分有必要对此重要问题进行进一步的深度分析.
在两类创新与经济增长机制这一领域中,除了以上理论机理的分析文献外,也有部分实证分析的文献.在实证研究方面,由于研究对象、样本区间、研究思路等方面的差异,国内外已有文献在分析不同类别创新对经济增长的作用中,所得结论也是各色各样,不尽相同,甚至截然相反.例如,国外Czarnitzki和Thorwarth[20]发现基础类创新对经济增长有促进作用,尤其是在高技术公司中,基础类创新是其经营成功的关键因素,基础类创新占比提高对企业的产出有更大的正向作用,且基础类创新对高新技术公司有更大的溢出作用,但对低技术公司几乎没有影响;类似的,Luintel和Khan[21]认为基础类创新对经济增长和全要素生产率有正向的促进作用,并且该作用是长期的.另外,You和Jiang[22]发现基础类创新对经济增长的正向作用存在滞后性,但认为应用类创新对经济增长正向作用比基础类创新更强.然而,Kim等[23]发现韩国的基础类创新对经济增长的正向促进作用不显著;Coad等[24]对西班牙制造企业样本进行分析,在研究中发现不同的公司有其各自的创新研发策略,格兰杰因果检验支持应用类创新更能促进企业提高生产率;Solomon[25]也发现了类似的结果,而且还发现了两类创新之间的互补性.国内叶祥松和刘敬[5]发现基础类创新在短期内对提高全要素生产率没有直接影响,从而对经济增长没有直接影响;然而,严成樑和龚六堂[3]与陈钰芬等[26]却发现基础类创新对经济增长或效率有促进作用.对于应用类创新对经济的作用而言,贺俊等[17]通过面板数据回归发现应用类创新的比例越高,经济增长的速度越慢,这在叶祥松和刘敬[5]的研究中也得到支持;而陈钰芬等[26]与孙早和许薛璐[18]等研究则支持应用类创新对经济增长或效率有正向作用.
综合以上国内外有关创新与经济增长之间的理论与实证文献可以看出,虽然近年来国内外相关领域取得了丰硕成果,但是结合中国的现实特征来看,已有研究主要有两点显著不足:第一,现有国内文献理论上普遍只考虑了基础类创新通过影响应用类创新,进而影响经济增长的单向直接传导路径,未能在理论机制上考虑应用类创新对基础类创新的反馈效应;近年来部分国外研究中虽然包含了两类创新的反馈效应特征,但是未能准确反映和刻画中国两类创新之间的真实现状,与现实事实所反映出的信息不完全一致.反馈效应从根本上改变了原有文献中两类创新单向直线形的狭义传导路径的认识,它决定着创新的结构构成和系统效能.反馈效应在现实中具有真实性,它不应该被忽视.第二,现有文献理论上普遍忽略了基础类创新对经济增长的直接作用,未能充分注意到基础类创新、应用类创新和经济增长之间是具有反馈效应的网络化传导机制.它隐含着基础类创新、应用类创新和经济增长之间形成了具有内在动态循环功能的有机统一体,由此根本上突破了原有文献简化的单向直线形传导模式的缺陷,更加符合现实创新和经济增长之间的系统性作用机制.同时,已有国内外实证研究,特别是国内实证研究,在缺乏基础类创新、应用类创新和经济增长之间具有反馈效应的网络化传导机制理论研究的基础上,有的文献贸然将基础研究、应用研究、试验发展等创新变量直接放入计量模型作为解释变量对经济增长进行回归实证分析,极大可能会由于缺乏正确的经济学理论行为机理的指导而导致相关经验分析偏离现实,并出现研究结论的随意性和不准确性.
2 两类创新的反馈效应及其与经济增长网络化传导机制的理论模型构建
为了能更清晰的阐述经济增长和两类创新之间的关系,借鉴Romer[27]、Jones[16]、严成樑和龚六堂[3]以及周建和周杨雯倩[28]等文献,考虑两类创新在经济体中的结构和反馈效应.模型主要由家庭、最终产品生产商、中间产品生产商以及创新部门构成,在创新部门中存在应用类和基础类两类创新活动.由于不讨论政策的影响,简化了对政府部门的设定.
2.1 家庭
假设没有人口增长,每期家庭的时间禀赋量纲化为1,代表性家庭在预算约束下通过选择消费C以及用于劳动力再生产的劳动数量uHH最大化自身的效用,有
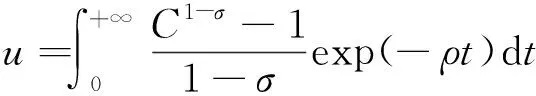
(1)
式中C表示消费;ρ表示消费者每期的贴现率;σ表示消费者跨期替代弹性的倒数.u中uY为用于最终产品的生产部分的劳动,uH为用于劳动力再生产部分的劳动,uF为用于基础类创新生产部分的劳动,uA为用于应用类创新生产部分的劳动.家庭的预算约束表示为
(2)
式中r是资本K的价格;w是每单位劳动的工资;H为社会劳动力存量;τ表示政府部门对家庭一次性征收的税,用于支持由政府主导和支持的基础类创新活动.劳动的积累方程为
(3)
式中ξ表示劳动力再生产的生产率参数.
个体在预算约束下使得效用函数最大化,由一阶条件以及横截性条件可得
(4)
r-gw=ξ
(5)
式中gC为消费的增长率;gw为工资的增长率.后文均用gi表示变量i的增长率.
2.2 最终产品生产部门
最终产品生产部门生产函数采用Cobb-Douglas规模报酬不变的生产函数形式,借鉴Torre和Marsiglio[29]的Uzawa-Lucas模型中对全要素生产率的扩展,将社会中基础类创新存量F引入生产函数中,依据Funke和Strulik[30]以及Arnold[31]中生产函数的设定,将其设为
Y=FKβDη(uYH)1-β-η
(6)
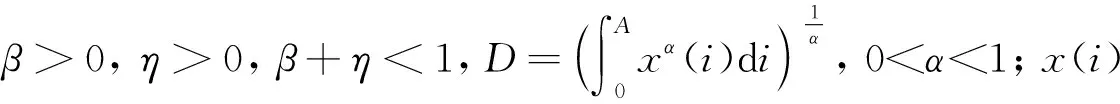
(7)
式中p(i)为第i种中间品的价格.将最终产品每期的价格单位化,求出式(7)的一阶条件,可得到最终产品部门对资本、中间品和劳动的需求函数为
(8)
(9)
(10)
2.3 中间品生产部门
中间品生产部门用部分最终品作为投入,通过创新部门所生产的技术将其转化为最终生产部门所需的中间商品,由在[0,A]上无限个生产商组成,其所使用创新部门的技术假设存续无限期.由于其生产商品的特殊和多样性,将其设定为由一系列垄断厂商组成.他们购买创新部门的技术用最小的代价将一单位最终品z(i)转化为一单位中间产品x(i).为简便,假设中间品生产部门可以无成本的将中间品和最终品投入相互转化,并且无折旧,即x(i)=z(i).每一个中间品生产商选择生产数量使自己的利润最大化maxxp(i)x(i)-x(i).由于垄断者面临单调递减的需求曲线,边际成本不变的厂商面对需求弹性不变的市场需求,定价由边际成本加成决定,从而p(i)=1/α.由于技术和需求对于所有中间品生产商来说都是相同的,根据对称性,x(i)=x,p(i)=p,所有中间品投入为Ax=αηY,每个中间品生产商的利润为
(11)
可得
(12)
将式(12)代入式(6)可得最终产品生产部门的生产函数
Y1-η=(αη)ηFKβA(1-α)η/α(uYH)1-β-η
(13)
2.4 两类创新部门
从两类创新的分类来看,基础类创新作为应用类创新的基础,必然会对应用类创新存在影响,但是随着技术边界不断拓展,应用类创新在不断应用实践的过程中触及新兴领域,反过来会刺激和催生前沿理论的发展,形成对基础类创新的反馈效应,即两类创新之间不是单向的影响路径,而是具有反馈效应的复杂传导途径.由此可见,应用类创新同时以基础类创新和自身发展现状为基础,基础类创新不仅在自身存量的基础上扩展,而且也可能会由应用类创新催生出新的研究方向,扩展创新的边界.这一现象不仅具有一般性的特征和意义,而且就中国而言,更符合中国在投资驱动阶段中以消化吸收为主的创新模式,即通过新技术的引进可能会催生和引发新的基础类创新方向.因此,在设定两类创新生产函数时会充分考虑这一特性所带来的差异.
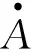
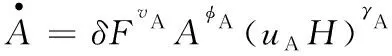
(14)
式中φA为自身的产出弹性;υA为基础类创新对应用类创新的反馈效应;γA为应用类创新劳动弹性;δ为相应的生产率参数,δ>0.
基础类创新在现有科学研究的基础上进行扩展和深化,但同时也可能会由于应用类创新中前沿技术的应用衍化出新的方向,扩展创新的边界,由此可见,基础类创新的生产与应用类创新存在差别.在我国以消化吸收为主的创新模式逐渐向自主创新为主转变的现实情况下,应用类创新对基础类创新的边界扩展作用与基础类创新自身的积累推进作用既可能同时存在,也可能只有基础类创新自身发挥作用,这取决于两类创新之间反馈效应状态的变化.因此,考虑到两类创新相互间的反馈效应在形式上存在着差异,同时又便于模型简化分析,此处将基础类创新函数设定为
(15)
式中υF为应用类创新对基础类创新的反馈效应;φF和γF与式(14)中定义相同.
式(15)表明,随着两类创新存量在基础类创新函数中密集度(φ1,φ2)的变化,两类创新存量在基础类创新生产函数中的作用呈现差异,也就使两类创新之间的反馈效应呈现出前文所阐述的现实状态.从中可以看出,基础类创新的扩张不仅可以在自身的肩膀上,同时也可以由应用类创新应运而生,两类创新活动在基础类创新过程中存在互补关系.在经济体中应对其优化,可以保证经济实现最优增长路径.假设两类创新部门的劳动可以自由流动,应用类创新的利润函数为
(16)
式中v为应用类创新的价格,大小等于中间品生产部门的利润折现值
(17)
式(17)表明应用类创新部门向中间品生产部门出售应用类创新所设定的价格等于中间品生产部门未来所有的垄断利润之和的现值,使得中间品生产部门是否生产均具有零利润.将式(17)对时间t求导,可得
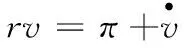
即
(18)
进一步根据应用类创新的利润函数,对式(16)求得一阶条件为
(19)
由于基础类创新具有基础服务性功能,类似于高校和研究所等科研机构,假设相应产出作为社会知识存量不能直接在市场中取得收益,政府财政支持是其经费来源的主要途径,为了简化分析,假设政府部门收入来源于税收τ,并用于对基础类创新活动的支持,可表示为
τ=wuFH
(20)
3 模型求解以及稳态性质分析
根据预算约束式(2),结合式(11)、式(16)以及式(20),可得出
(21)
进一步结合式(8)和式(9),可得
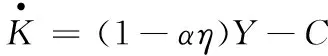
(22)
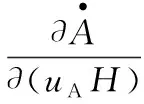
(23)
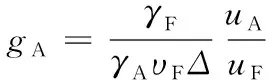
(24)
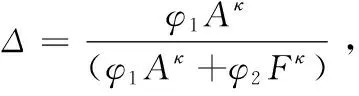
gΔ=κ(1-Δ)(gA-gF)
对最终产品生产函数式(13)、利率表达式(8)、工资表达式(9)、式(19)和式(20),分别取对数后对时间求导,可求出
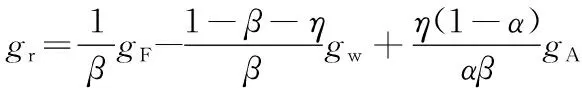
(25)
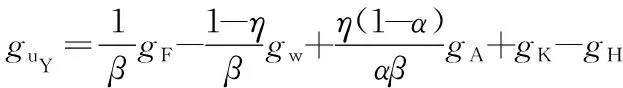
(26)
gw=gY-guY-gH
=υAgF+φAgA+(γA-1)(guA+gH)+
=gT-guF-gH
(27)
由式(11)、式(19)以及式(9)可知
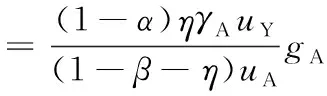
(28)
结合式(5),式(22)~式(24),式(26)~式(28)可以求出相关变量增长率,可知经济系统由K,H,A,F,C,uY,uA,uF变量驱动.在平衡增长路径上,均衡数量序列{C,K,H,A,F,uY,uA,uF}以及均衡价格{pY=1,p(i),r,w,v,i∈[0,A]}满足以下条件:
1)效用和利润最大化
a.消费者效用最大化.给定一系列价格,消费序列C使得消费者在预算约束下实现效用最大化.
b.最终产品部门利润最大化.给定一系列价格,最终产品生产商选择{uY,K,x(i),i∈[0,A]}使之实现利润最大化.
c.中间品生产部门利润最大化.给定最终产品部门对中间品的需求曲线,中间品生产部门决策{p(i),x(i),i∈[0,A]}使之实现利润最大化.
d.创新部门利润最大化.给定工资,创新部门投入相应的劳动使之实现利润最大化.
2)市场出清
a.劳动市场. 最终产品部门、各创新部门以及劳动力再生产所需的劳动总和为劳动力的累积数量,即(uY+uA+uF+uH)H=H.
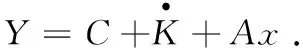
c. 创新市场.给定利率,应用类创新产出的价格等于中间品生产部门未来各期的利润流的折现和.
性质1由上述动态经济过程驱动的相关变量在平衡增长路径(BGP)上是恒定的.
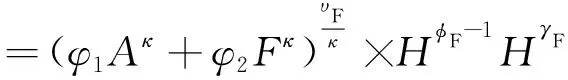
根据θ、ϑ、q、χ在BGP上为常量以及gY=gC=gK且guY=guA=guF=0,可求出所有变量处于平衡增长路径时的增长率,以及每个部门所用的劳动比例,具体为
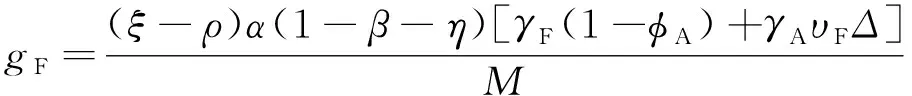
(29)
(30)
(31)
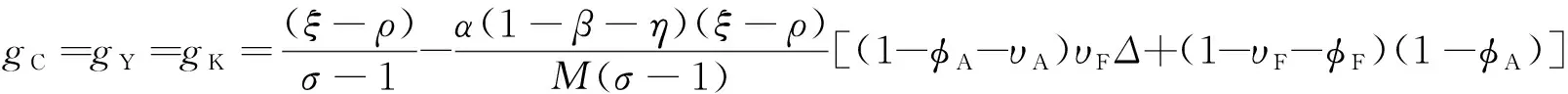
(32)
(33)
[(1-φA)(υFΔ+1-υF-φF)-υAΔ]
(34)
式中
M=(σ-1)γAυF[α+η(1-α)]Δ+ασ(1-β-η)(1-φA-υA)υFΔ+(σ-1)γF[α(1-φA)+
由于Δ是两类创新存量的函数,随着Δ大小的不同以及两类创新增速处于不同的状态,两类创新对经济增长的作用也不尽相同.由于gΔ=0可知,必有gA=gF或κ=0或Δ=1成立,因此将3种情形下Δ的取值代入式(32)后,可以得到以下推论.
推论1.1当满足gA=gF时,则有γA(1-υF-φF)=γF(1-υA-φA)成立,此时Δ可由三次方程确定唯一解(1)从式(23)和式(24)相等可以得出gF,联立式(29)后为三元一次方程,则必有实根.由于实现经济增长率最大的为最优解,因此必有唯一解.,并且基础类创新生产函数是关于两类创新的CES生产函数.此时经济产出稳态增长率为
式中
M=(σ-1)γAυF[α+η(1-α)]Δ+ασ(1-β-η)(1-φA-υA)υFΔ*+(σ-1)γF[α+η(1-α)]×
(1-φA)+ασ(1-β-η)(1-φA)(1-υF-φF)
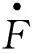
推论1.2.1在Δ=1成立条件下,此时经济产出稳态增长率为
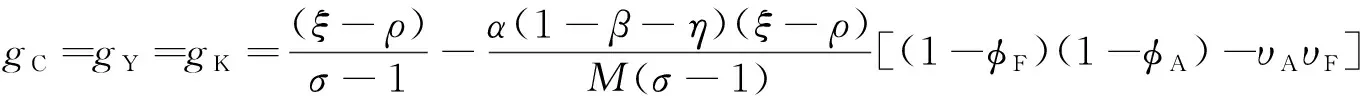
式中
M=(σ-1)α[γAυF+γF(1-φF)]+η(1-α)(σ-1)[γA(1-φF)+γFυA]+ασ(1-β-η)×
[(1-φA)(1-φF)-υAυF]
推论1.2.2在κ=0成立条件下,可得Δ=φ1/(φ1+φ2),则经济产出稳态增长率为
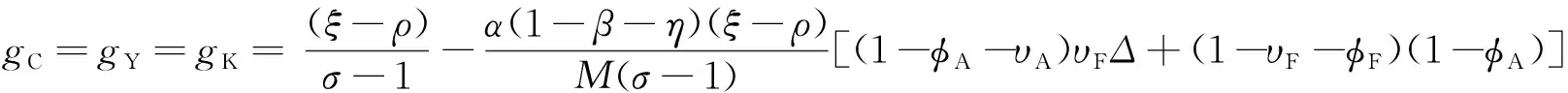
式中
M=(σ-1)γA[α+η(1-α)]υFΔ+ασ(1-β-η)(1-φA-υA)υFΔ+(σ-1)γF[α(1-φA)+
η(1-α)υA]+[η(1-α)(σ-1)γA+ασ(1-β-η)(1-φA)](1-υF-φF)
性质2应用类创新(基础类创新)参数系统υA、φA、γA(υF、φF、γF)中每一参数各自对产出增长率的影响具有条件依附性和非恒常性走势,即每一参数对产出增长率的影响特征具有条件约束,在不同的约束条件下具有不同的函数特征和图形走势;在同一条件下,不同参数对产出增长的影响存在差异性.具体结论如表1所示.
经济增长率在基础类创新生产函数处于不同情形时具有条件依附性和非恒常性走势.当两类创新的生产函数满足规模报酬递增时,随着两类创新生产函数参数逐渐增加使经济增长率趋于无穷,在此不作讨论.当两类创新的生产函数满足规模报酬递减或不变的特性时,即满足υA+φA+γA≤1且υF+φF+γF≤1条件下:1)当υF>0时(见表1中I,a和II,a),随着两类创新存量在各自生产函数中的弹性φA和φF的增加,其对经济增长的作用越来越大;随着两类创新劳动弹性γA、γF的增加,其对增长率的增长作用越来越小;而两类创新相互间的反馈效应(υA,υF)对增长率的影响形态则取决于其与γA和γF的关系:若同时满足υF>(σ-1)γFη(1-α)/[ασ(1-β-η)],υA>(σ-1)γAα时,随着υA,υF的增加,其对经济增长的作用越来越大,即当一类创新对另一类创新的反馈效应大于另一类创新劳动弹性的一定比例时,随其增大,其对经济增长率的作用呈现爆炸式效果.2)当υF<0时,(见表1中I,b和II,b),随着基础类创新函数参数(υF、φF、γF)的增加,其对经济增长率有正向作用;随着应用类创新函数参数(υA、φA、γA)的变化,其对经济增长率作用的正负效果随着υF(挤出程度)大小而定(例如在Δ=1的情形下,当满足υF<-η(1-α)(1-φF)/α时,则υA、φA、γA逐渐增大,对经济增长率有负向作用).
从生产函数性质来看,1)当υF>0,从表1中I,a和II,a可知,当Δ=φ1/(φ1+φ2)时所确定的经济增长率高于Δ=1时所确定的经济增长率;2)当υF<0时,从表中I,b和II,b可知,Δ=φ1/(φ1+φ2)情形下所决定的经济增长率随着υF的增大而实现逐渐趋同于Δ=1的情形,并于υF=0处两者相等,即在υF由负变正的过程中,Δ=φ1/(φ1+φ2)时所确定基础类创新生产函数中关于F的弹性由低水平向高水平转变.因此,应用类创新对基础类创新的反馈效应υF在挤出到挤入变化的过程中,两类创新存量结构对经济增长的作用存在条件性转换,并且应用类创新函数参数对经济增长率的作用也存在条件依附性和非恒常性走势,形成了不同的最优经济增长模式.
当两类创新增长率相等时(即gA=gF,表1中III),不能单独看某一参数的变化,这是由于在参数变化过程中,需要维持γA(1-υF-φF)=γF(1-υA-φA)等式恒成立,因此,经济增长率随参数变化的过程是以关于其中任意两个参数的三维图所呈现.若两类创新中的参数同时增大,则可使得经济增长率提高,其中劳动弹性(γA、γF)的增加对gY提升的贡献越来越小,而两类创新的产出弹性(φA,φF)和反馈效应(υA,υF)的增加对gY提升的贡献则越来越大.
性质3在创新结构上,两类创新增长率的关系为
若Δ=φ1/(φ1+φ2),则有
[γAφ1(1-φF)+γAφ2(1-φF-υF)+
γFυA(φ1+φ2)]gF
若Δ=1,则有
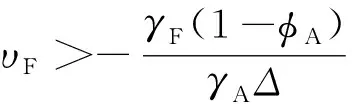
推论3.2在满足Δ=φ1/(φ1+φ2),γA(1-φF-υF)>γF(1-φA-υA)条件下,则有gA>gF(见表2).随着两类创新存量在基础类创新函数中的密集度φ1、φ2不同,两类创新的增长率关系gA/gF随着基础类创新密集度φ2的降低或者应用类创新密集度φ1的增加而降低.因此在应用类创新增长率gA相对更大时,若要进一步提高gA,则应提高基础类创新密集度φ2;若要进一步提高gF,则应提高应用类创新密集度φ1.
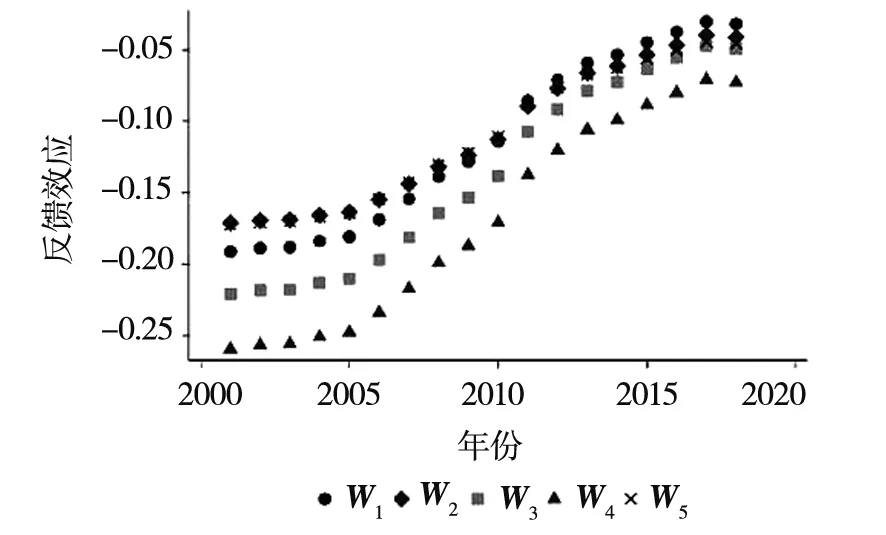
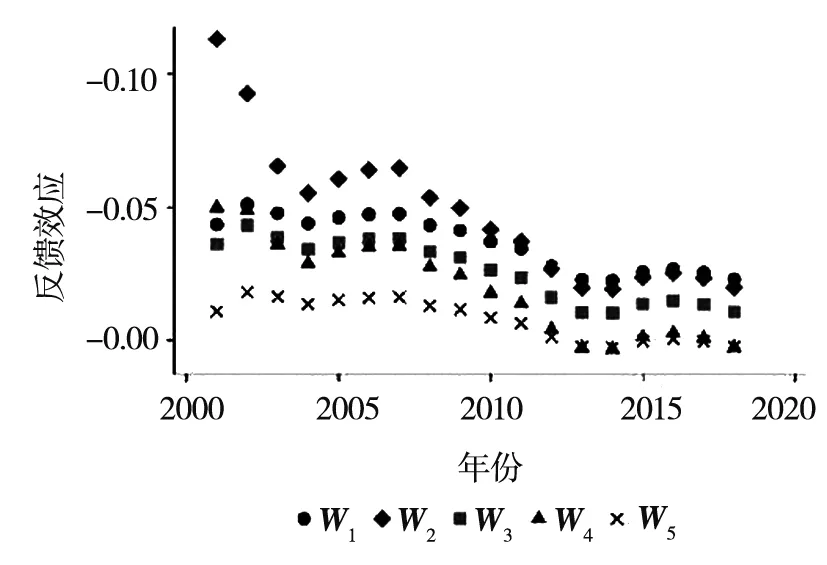
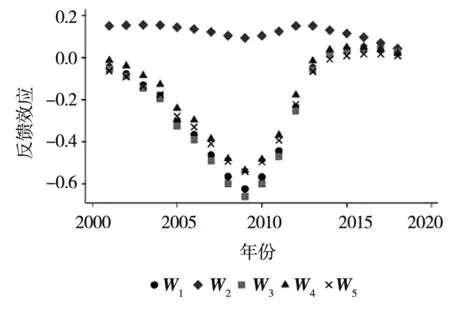
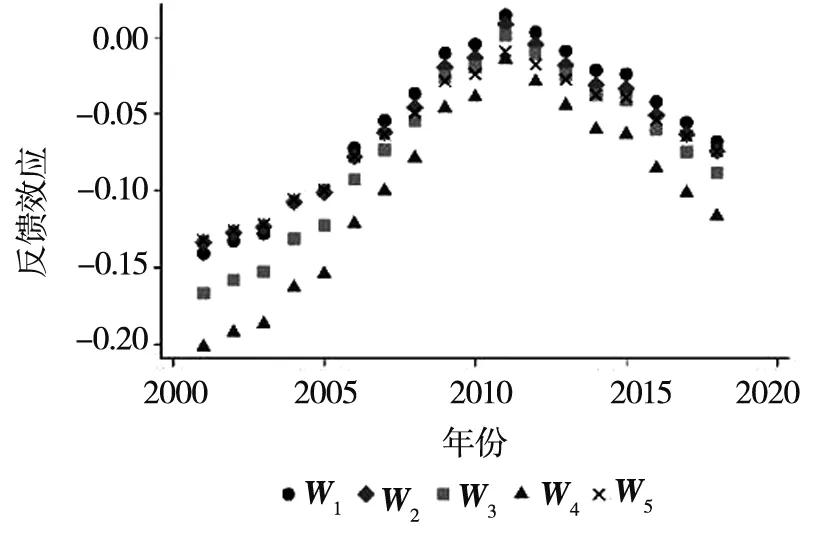
推论3.3在满足Δ=φ1/(φ1+φ2),γA(1-φF-υF)<γF(1-φA-υA)条件下,则有gA 表2 推论3.2和推论3.3Table 2 Corollary 3.2 and corollary 3.3 应用类创新主要包含试验发展活动,活动主体是企业[6],相应主要产出是以专利为代表[32].这一特征首先主要表现在创新投入上,在样本期间内,企业用于应用类创新支出的比重约95%,占社会的应用类创新支出的比重为88%,其次表现在创新产出上,企业专利申请占社会专利申请总量的90%.因此,应用类创新产出选用专利申请量作为代理变量,相关创新投入数据用企业创新投入数据作为代理变量. 基础类创新包含基础研究和应用研究活动,主要由高校和科研机构承担[3-6,17],从样本期间内的事实数据来说,高校和科研机构的基础类创新经费支出占全社会基础类创新经费的比例约为77.4%,但是高校和科研机构的科研经费支出仅占社会经费支出的27.9%,可见高校和科研机构的全部科研经费在社会中的占比偏低,但却占全社会基础类创新经费的绝大部分,因此,高校和科研机构作为社会基础类创新的主体是合理的.另外,从研发活动的定义、内涵,以及许合先[33]、陈凯华等[34]等一系列文献均表明科技论文数量可以代表我国基础研究水平,从样本期间内的事实数据来说,在成果方面高校和科研机构的专利申请数量仅占社会专利申请数量的10%左右,而国外主要检索工具收录我国发表的科技论文数量约81.98%来源于高校和科研机构,因此,基础类创新产出选用国外主要检索工具收录我国发表的科技论文数量作为代理变量,相关创新投入数据用高校和科研机构创新投入之和作为代理变量. 以中国大陆30个省市自治区(不包含西藏自治区,因其大部分数据缺失)的面板数据作为对象来进行实证检验,样本区间为2000年~2018年,数据来源于各年的《中国统计年鉴》与《中国科技统计年鉴》.两类创新存量采用严成樑等[35]的方式计算而得,通过永续盘存法 Ait+1=(1-d)Ait+Pit 式中Pit为第i个省份第t年创新产出增量,表示创新流量;d为创新存量的折旧率. 参考国内外大多数研究的设定,将折旧率分别取值为0%、5%、10%和15%,估算出相关创新存量.由于相关结果差异不大,篇幅有限,此处只列出15%的结果. 根据应用类创新生产函数的设定(式(14)),考虑其中所包含的要素,作为应用类创新产出回归模型构建的基础.在空间上创新呈现创新集群或者正向的溢出效应[36],在此对省级面板数据的空间特征进行控制,进一步验证创新的空间影响关系,由此将应用类创新产出的回归模型设为 XiAtβA+di+uiAt,t=1,…,T (35) 基础类创新产出的变化不仅受到该类创新存量的影响,而且应用类创新对基础类创新具有反馈效应.根据式(15)中所表达的关系,基础类创新不仅来源于现有的知识体系,而且新技术等应用类创新也可能会使得基础类创新有持续的发展,对基础类创新具有反馈效应.参考式(15)中所包含的要素,并与应用类创新类似,考虑了创新的空间溢出效应,将基础类创新产出的回归模型设为④ XiFtβF+di+uiFt,t=1,…,T (36) 证模型设定 现有大量研究表明省际经济增长存在空间溢出效应[38],根据前文可知,理论上应用类创新直接对经济增长有影响,而且基础类创新也可能对经济增长具有直接影响.根据式(13),此处设定经济增长的回归模型时除了考虑将应用类创新作为解释变量外,还引入基础类创新作为解释变量,建立回归模型 lnYit=χ1WlnYit+XiYtβY+ζlnAit-1+ (37) 式中Yit为以2000年为基期的人均GDP值;控制变量XiYt为解释经济增长的其他解释变量,包括:资本存量(lnKit),人力资本(lnHit),产业结构(第二产业比重和第三产业比重),政府支出规模(govexp_gdpit,用政府支出与GDP之比表示)和开放性水平(maoyi_gdpit,用进出口总额与GDP之比表示).资本存量采用张军等[39]的方法进行核算,并采用以2000年为基期的人均对数值表示;人力资本采用严成樑和龚六堂[3]的方法,通过6岁及以上人口的平均受教育年限来衡量经济中的人力资本水平.教育程度包括小学、初中、高中、大专及以上,不同教育程度对应的教育年限也不同,其中小学为6年,初中为9年,高中为12年,大专及以上为16年.用各类受教育人口占总人口的比例乘以各类教育对应的教育年限计算平均受教育年限,取对数值后作为人力资本的代理变量.两类创新存量的人均对数值,采用永续盘存法进行计算.uiYt是回归模型的随机误差项. W为经标准化处理后的30×30阶空间矩阵.为了从多方面体现结果的稳健性,从自然和经济两个角度基于多种情况选择5种空间矩阵进行分析,分别按照空间位置是否邻接(W1)、地理距离(W2)、经济距离(W3)、经济距离兼区位因素(W4)、经济距离兼板块因素(W5)进行设定.空间邻接矩阵W1表明当第i和第j个省自然位置相邻,矩阵中wij=wji=1;地理距离矩阵W2基于省会城市实际地理距离构建;经济距离矩阵W3中wij=(1+2|Lnpgdpi-Lnpgdpj|)-1,其中Lnpgdpi表示第i省人均GDP在样本时间区间中平均值的对数值;经济距离兼区位因素矩阵W4在经济距离空间矩阵W3的基础上加入了区位因素,区位的划分为:东部包括北京、天津、河北、上海、江苏、浙江、福建、山东、广东和海南;中部包括山西、安徽、江西、河南、湖北和湖南;西部包括内蒙古、广西、重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏和新疆;东北包括辽宁、吉林和黑龙江,如果两地所属区位相同,则按W3的方法取经济距离作为矩阵元素,否则取0;经济距离兼板块因素矩阵W5是在W3的基础上加入了板块因素,板块的划分为:华北地区包括河北、山西、内蒙古、北京、天津;东北地区包括辽宁、吉林、黑龙江;华东地区包括山东、江苏、安徽、浙江、福建、江西、上海;华中地区包括河南、湖北、湖南;华南地区包括广东、广西、海南;西南地区包括重庆、四川、贵州、云南;西北地区包括陕西、甘肃、青海、宁夏、新疆,如果两地所属板块相同,则按W3取经济距离作为空间矩阵元素,否则取0. 就空间关系来说,考虑到两类创新增量和经济增长均存在空间效应,而且两类创新与经济增长之间呈现网络化传导机制,因此3者的误差项可能具有相互影响并造成参数估计无效的问题,为此,建立空间面板SUR模型.另外,为了进一步考虑方程系统之间的相关性以及避免信息遗漏,并且更为准确合理地刻画两类创新之间的演变机制及其对经济增长的网络化关联效应,还在三个方程的误差项中考虑空间相关性,以便于对于方程系统中可能存在的外生的空间效应进行更为充分的设定和捕捉,即针对上述模型系统的误差项进一步设定空间形式:uimt=ΛWuimt+εit,m=A,F,Y.参考现有文献[40],对该模型系统进行3SLS估计.同时为了避免控制变量的内生性,模型设定中的控制变量采用其滞后1期形式.估计过程中,针对内生的空间滞后项采用的工具变量为外生变量的空间滞后项.回归结果如表3所示. 表3 两类创新演变机制及其对经济增长网络化传导机制的回归结果Table 3 Regression results of evolution mechanisms of two types of innovation and the network transmission mechanism among two types of innovation and economic growth 续表3Table 3 Continues 对于应用类创新形成机制的回归结果而言,其存量对下一期具有显著的正向影响,而且在5种空间权重设定下其产出弹性φA在90%以上,表明了应用类创新产出数量呈现明显的动态惯性特征,应用类创新的产出量显著依赖于上1期存量;基础类创新对于应用类创新的反馈效应为正且显著,在5种空间权重设定下均显示其影响弹性υA为3%左右.不同空间矩阵下,各省第二产业比重在方程中对应用类创新产出的影响为正,但第三产业比重在5种矩阵下对应用类创新产出的影响不显著,其原因可能主要在于应用类创新活动大部分集中于工业企业,因此,第二产业的发展对其有不可忽视的影响. 图2 反馈效应Fig.2 Feedback effect 从时间变化的角度来看,各省反馈效应的变化大体呈现4种类型:逐年递增型、逐年递减型、正“V”型和倒“V”型.具体来说,辽宁、海南和新疆的反馈效应呈现逐年增加的趋势,天津、上海、江苏和湖北呈现逐年递减的趋势,北京、吉林、陕西和甘肃呈现下降后上升的正“V”型变化过程,其余大多省份表现出先上升后下降的倒“V”型变化,且大多在2010年左右达到最大值.图3(a)-图3(d)4个图中针对上述4种情形选取了代表性省份进行绘制,可以看出各省的反馈效应既存在共性,又有呈现差异化的变化趋势.这一特征是由两类创新在不同情形下的内在演化机制决定的.控制变量中,各省基础类创新经费投入(lprdex_brit)和劳动投入(lprdl_brit)对其产出具有正向作用,而政府对基础类创新的支持程度(govf_brit)对基础类创新产出有负向作用,但在不同的矩阵下显著性存在一定差异,这一结果与冯宗宪等[38]有类似的结论,现实中政府干预程度过高在一定程度上可能会导致创新呈现滞后性、片面性、失误率高和由于寻租被扭曲等特点和现象,因此,在基础类创新生产中引入市场机制,并充分发挥企业和市场的作用十分有必要. (a)逐年递增型(代表省份: 海南)(a) Incremental year by year (for province: Hainan) (b)逐年递减型(代表省份: 上海)(b) Decreasing year by year type (for province: Shanghai) (c)正“V”型(代表省份: 甘肃)(c) Is a “V” type (for province: Gansu) (d)倒“V”型(代表省份: 河北)(d) Inverted “V” type (for province: Hebei)图3 四种类型的反馈效应Fig.3 There are four types of feedback effect 对于两类创新对经济增长网络化传导机制的回归结果而言,在5种空间矩阵下,两类创新对经济增长均有促进作用,应用类创新存量对经济增长有直接的促进作用,而基础类创新存量对经济增长的作用在5种空间矩阵下均为正且显著,这说明基础类创新不仅可以通过影响应用类创新进而影响产出,其本身对经济增长也有直接的促进作用,由此找到了基础类创新直接影响产出的实证证据.同时,在经济学的政策分析内涵上,实证计量结果显示,5种空间矩阵下,应用类创新对经济增长的弹性范围在3.08%到6.04%之间,数值相对接近.基础类创新对经济增长的弹性范围在4.82%到7.73%.从中可知,虽然基础类创新在现实和理论上推进和发展较应用类创新缓慢,但是它对经济增长的作用比应用类创新更强,在考虑发展两类创新与经济增长协同的相关政策时应充分关注、挖掘和利用基础类创新的作用. 本文创新性地从中国两类创新的反馈效应和网络化传导机制的视角研究了两类创新及其与经济增长的协同演化机理,克服了已有文献仅考虑基础类创新对应用类创新的单向作用,进而影响经济增长的简单直线途径的显著不足.通过标准的数理经济学刻画和推导,系统分析了两类创新及其与经济增长的协同演化机理,在此基础上,进一步对中国两类创新的反馈效应及其与经济增长的网络化传导机制进行了翔实的实证分析和检验,主要结论如下. 1)理论分析表明,应用类创新(或者基础类创新)参数系统中每一参数各自对产出增长率的影响具有条件依附性和非恒常性走势.随着应用类创新对基础类创新的反馈效应处于不同的状态,经济增长会呈现差异.若处于挤入状态,提高基础类创新存量,使两类创新存量协同发展更有利于经济增长;反之,应偏重于应用类创新存量的积累.为了实现两类创新对经济增长的持续性作用,应加强两类创新生产中各生产要素的利用能力(弹性),尤其是要增强在新技术上的进一步创新研发,以实现应用类创新对基础类创新的反馈效应具有正向作用,并保证两类创新对经济增长正向刺激的协同作用. 2)在反馈效应和网络化传导机制下,创新结构具有确定的稳态构成.相关结构中,当两类创新增长率不同时,二者之比由两类创新生产函数的参数唯一确定,某类创新生产函数中任何一个参数的增大都会提高该类创新相对于另一类创新增长率的比值,但在不同的情形下,实现两类创新相对增长率的改变在措施方式上存在着差异.当应用类创新对基础类创新的反馈效应有正向挤入作用时,提升相应创新生产中各生产要素的利用能力(弹性)有利于提高其增长率;但当应用类创新对基础类创新呈现较大的负向挤出作用时,基础类创新对应用类创新作用的增大反而会阻碍应用类创新增长率的提高. 3)实证检验表明,中国基础类创新和应用类创新相互影响,存在着反馈效应.基础类创新对应用类创新的弹性影响系数大小约在3%左右,由此验证了基础类创新影响应用类创新的传统性认识.本文进一步拓展了上述认识,发现应用类创新对基础类创新也具有十分重要的非线性反馈效应,在我国不同省份不同时点的样本中,既有应用类创新挤入了基础类创新,又有应用类创新挤出了基础类创新,且当两类创新结构处于平衡发展的状态时,挤入效应明显.从时间的角度来看,在2000年~2018年期间,总体上各省的反馈效应虽有共性,但也呈现差异化特征.从两类创新与经济增长的影响机制来说,两类创新对经济增长同时具有十分显著的重要作用,基础类创新、应用类创新都会对经济增长产生重要的直接作用,而非传统所认为的简单的单向直线型传导途径,三者之间呈现出具有反馈效应的网络化传导机制.另外,两类创新与经济增长在各省之间也呈现出显著的空间溢出效应. 以上结论具有重要的现实意义和政策启示价值. 1)两类创新之间在理论和实证结果上均显示了具有反馈效应的双向传导路径.这表明,在我国科技创新政策方面,不仅要强调基础类创新对应用类创新的基础和引领作用,同时也应该关注应用类创新对基础类创新的反馈效应,并由此催生和造就可能的新兴基础类创新方向与分支.因此,在科技创新政策方面,要充分考虑反馈机制,同时结合实证证据,根据各省的差异化特征,合理设计和规划基础类创新与应用类创新的创新结构及其构成比例,做好系统匹配,使两类创新的结构处于平衡发展的状态,促使它们形成良性发展、相互促进、不断优化的动态演化格局,从而更好地促进我国科技创新能力提升.在具体政策设计上,需要关注:a)对于作为基础类创新主体的高校和科研机构与作为应用类创新主体的企业,需要着重对他们之间的协同性进行强化,充分鼓励校企创新合作,搭建合作平台,推动学校、科研机构等基础类创新成果应用于企业等应用类创新活动中,提升应用类创新的增长速度和质量.b)鼓励现有先进的应用类创新成果在高校和科研机构中的进一步研发,实现质量升级或者是新技术方向的突破,达到强化应用类创新对基础类创新正向反馈效应的目的.基础类创新不应仅由政府承担,而应努力构建有效的、保障多层次、多渠道的研发经费供给机制,实现政府投入、企业投入、银行贷款、社会集资等多元化多渠道配合.c)高校科研机构等基础类创新主体承担着创新人才的输出培育功能,真正加强产学研合作力度,促进两类创新活动相互间的正向反馈机制.在这样的前提下,从理论分析可知,提升两类创新的相关政策才能产生正向的协同作用. 2)基础类创新不仅通过影响应用类创新进而影响经济增长,而且基础类创新在理论和实证上也完全可能直接影响经济增长,即两类创新与经济增长之间存在相互影响的网络化传导机制.这说明我国在深入实施创新驱动发展战略过程中,应当清醒认识各类科技创新活动对经济增长的直接和间接综合作用,充分发挥它们的协同演化机理,尽可能形成两类创新之间相互促进的环境,优化并稳定两类创新的结构和规模,从而实现不同创新与经济增长之间的协同共促机能的合理性设计.在政策设计上,需要聚焦于:a)在良性循环促进的创新环境中,更要重视基础类创新的发展和积累,促使经济增长达到更优水平.在此过程中,高校、科研机构等部门在基础类创新中作为执行主体需要进一步激活活力,如激发科研人员的积极性和效率、加大基础类创新的投入力度、增强对现有前沿新兴领域创新成果的深化研究等,以实现基础类创新成果的加速积累和提升.b)政府应通过实施更加有效的财税创新政策、鼓励企业通过产学研合作等,增加企业对基础类创新的重视程度和投入力度,进一步实现和完善应用类创新对基础类创新的反馈支持功能.一方面,要加强应用类创新的增长和发展,充分发挥其生产效率提高对于经济增长的正向促进作用,在政策设计上,通过政府补贴、所得税减免等方式鼓励企业加大研发经费投入、降低创新主体进行创新的成本、扩大市场对新产品的需求潜力和降低创新商业化实现过程的风险等,有效提升应用类创新的效率.另一方面,还要综合优化两类创新与经济增长之间存在相互影响的网络化传导机制政策设计,以便于更好地在减少研发与经济增长网络结构内耗、增大各类研发创新种类促进经济增长输出流的过程中,不断系统地接近或达到基础类创新、应用类创新和经济增长之间的动态平衡,以此保障我国科技创新政策和经济增长之间的相洽性和有效性,从而最终实现创新引领经济转型升级,并实现我国经济的平稳健康增长. 3)我国两类创新以及经济增长在空间上均有正向的溢出效应.因为正向的溢出效应会减轻创新和经济增长在区域间的不充分、不平衡问题,所以我国不同省份、区域、板块之间的发展应突破行政区划界线,增加创新成果转化与对外扩散的力度和速度,通过完善和优化创新资源的配置,形成不同省份、区域、板块之间的协同创新格局.因此,我国在创新的区域政策设计和完善上:a)应着眼于加强和促进创新活动的跨区域合作交流,鼓励跨区域机构间形成帮扶关系,利用政治和经济激励导向开拓扶持渠道、支援形式等,加速带动欠发达地区的创新能力,通过发挥创新与经济增长的正向协同的良性机制作用,不断缩小地区间的差距,从而有效地实现我国不同区域的平衡发展.b)要加强、优化和完善人才、信息、知识等创新要素在不同区域间的自由流动政策设计.不同区域间的协同创新发展离不开创新要素的自由流动,因此,区域协同创新格局下要重视创新人才在不同区域间的交流和合作,通过信息和知识的共享平台实现人才、知识、要素的自由流动,以便于更好地实现创新资源的有效配置.经济欠发达地区自主创新能力相对较弱,更应创造良好的政策环境加速实现吸引优质的创新要素,不断提升吸收和消化经济发达地区外溢出的创新要素、创新资源和创新产出的能力,从而更好地实现自身创新与经济增长之间的良性协同演化.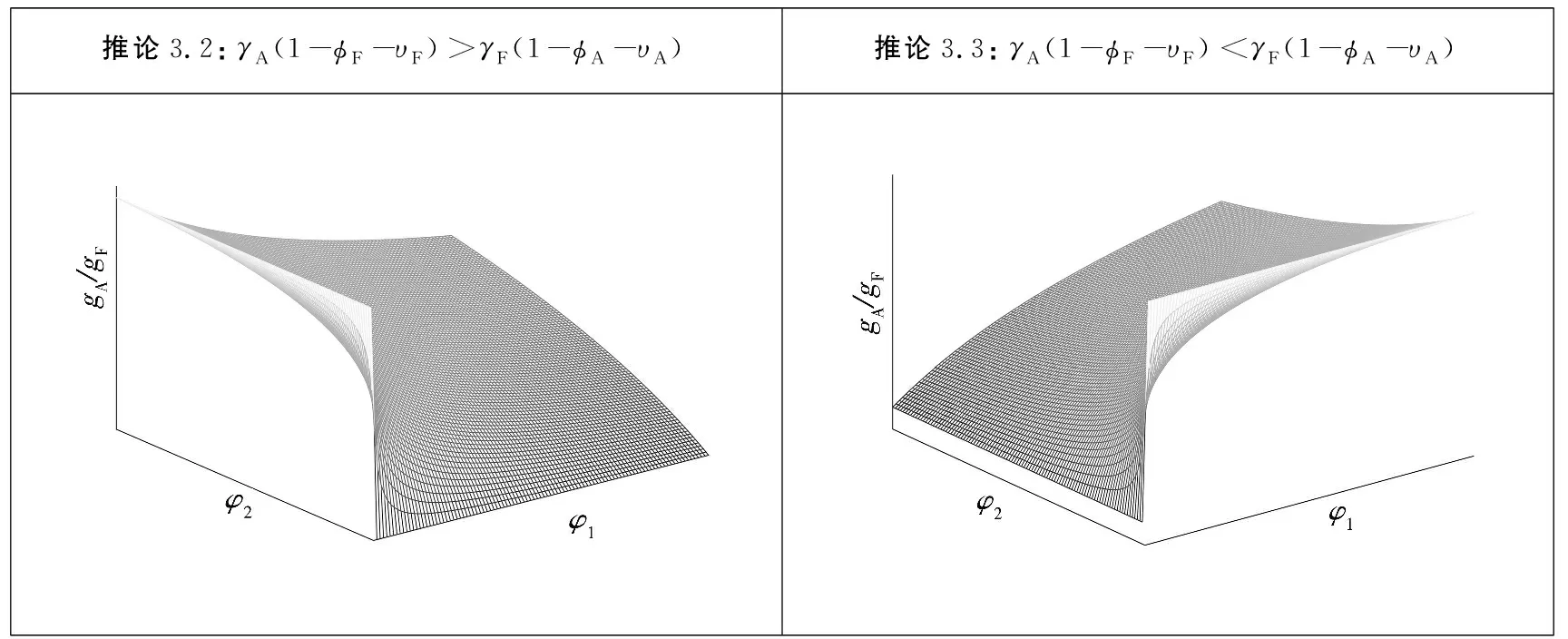
4 实证分析
4.1 应用类创新形成机制的实证模型设定
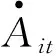
4.2 基础类创新形成机制的实证模型设定
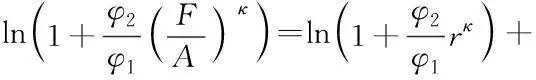
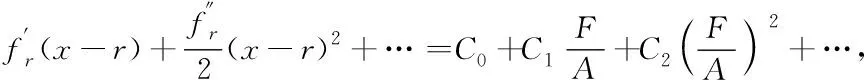
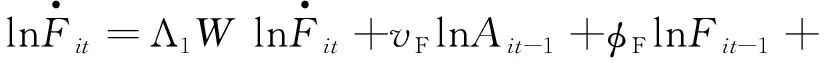
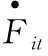
4.3 两类创新对经济增长网络化传导机制的实
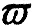
4.4 回归结果
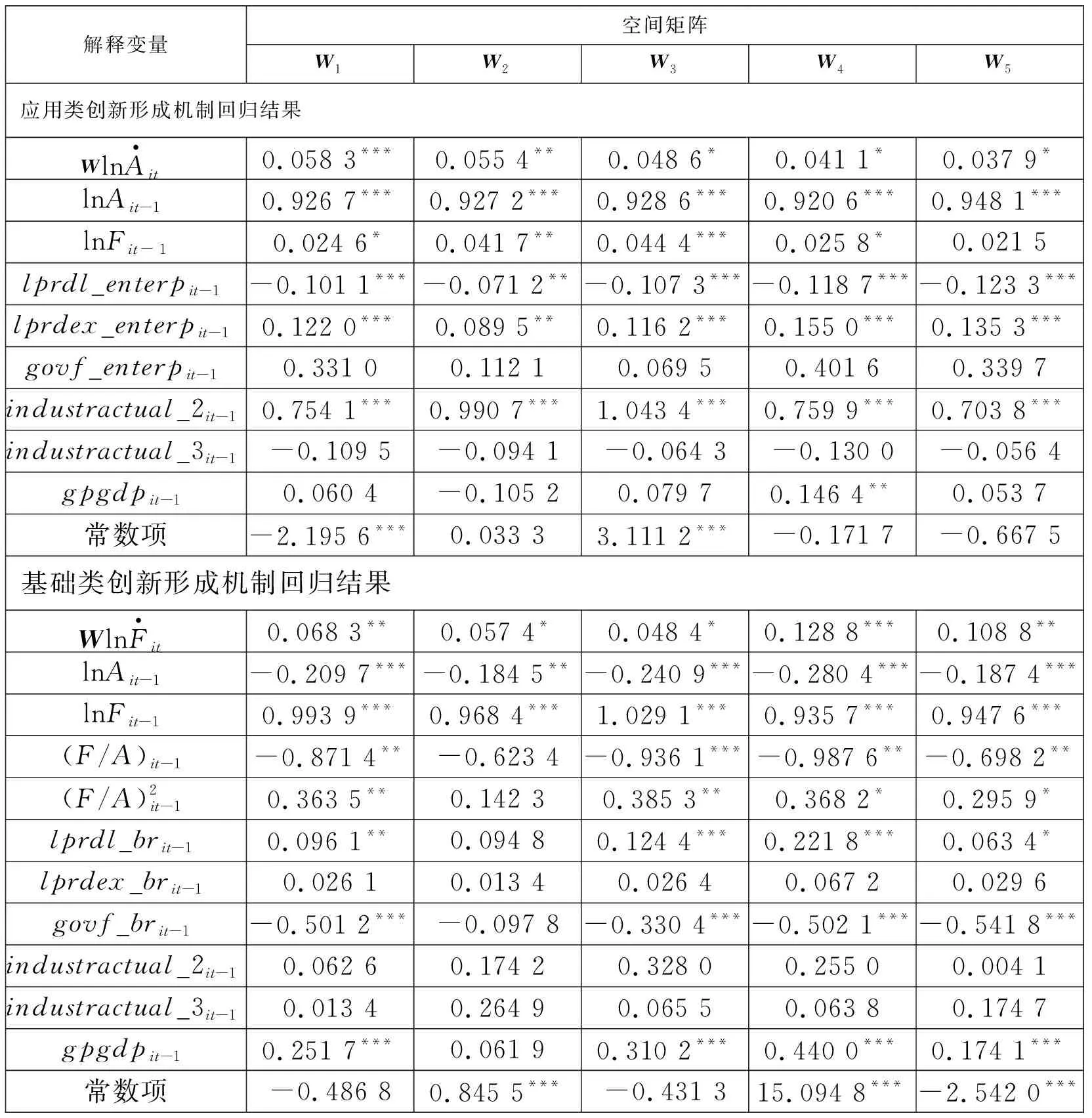
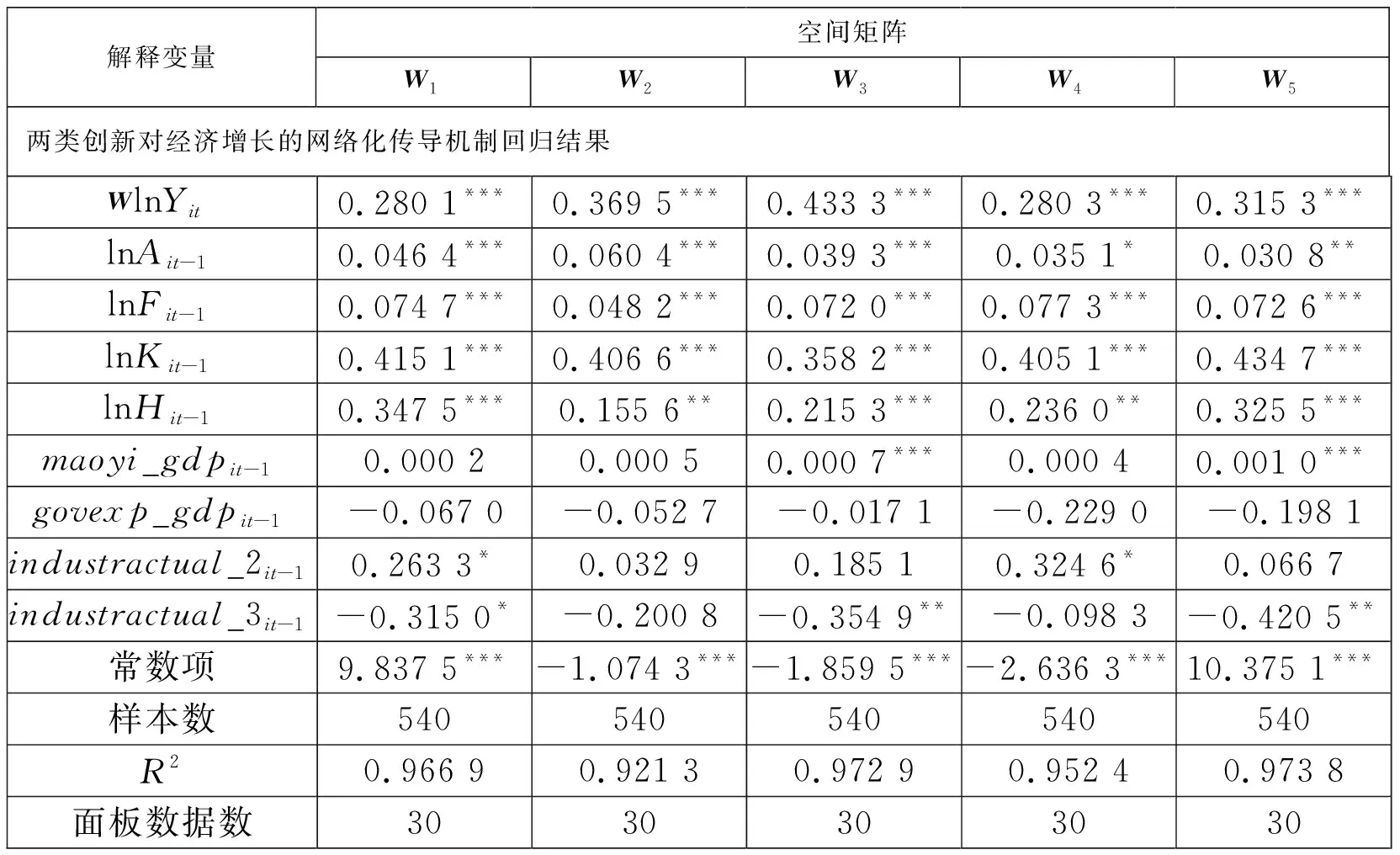
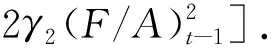
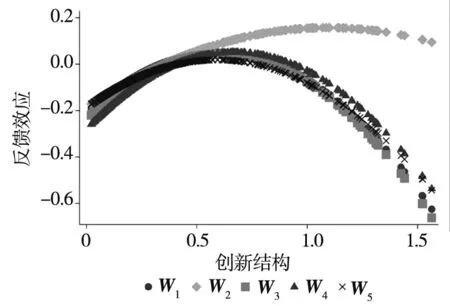
5 结束语

