一种基于音频技术的信息隐藏方法

田夏利

(武汉华夏理工学院，武汉 430223)

0 引言

扩展频谱通信，简称扩频(Spread Spectrum, SS)通信，是一种信息的传输方式，已融入到信息隐藏的各类方案中，成为提高鲁棒性的一项基本策略[1]。尽管其理论性能落后于量化方案，但改进后的SS抵消了载体的干扰，在低信噪比下能够获得与量化相近的性能，对使用SS技术嵌入信息的音频信号进行放大或缩小都不影响信息的提取，即使考虑数字化音频信号的饱和与有限精度效应，SS依然允许音频功率有几十dB的波动[2-3]。在图像隐藏中，载体信号幅度的变化通常较小，现有抗增益攻击的量化方案通常可适用，但在音频隐藏的实际应用中，信号幅度的调节很常见且波动范围较大，SS方案对增益不敏感的优势将更为明显[4-5]。

SS调制具有先天的自同步能力，即调制后的信号自身可用于同步而不需要额外的辅助信号。伪随机(Pseudo Noise，PN)序列的自相关通常具有尖锐的峰值，因此在携带信息的同时也可被接收端检测，从而实现同步。在很多不具备自同步能力的系统中，SS技术也常被用于同步码的设计和检测。SS技术可以视为信息隐藏的基本方案，在音频伪装中具有更多的先天优势[5-6]。

本文基于音频技术的信息隐藏方法，研究了载体对伪装信息的干扰影响，提出了一种边信息对伪装信息进行频域与时域联合整形的方案。

1 基于SS的音频伪装算法

1.1 改进SS调制

改进扩频(Improved Spread Spectrum，ISS)调制是对SS技术的改进,因此具备SS方案的所有优点,其基本策略是,在信息嵌入端实现信息解码的部分功能,从而在发送端计算载体在接收端的干扰量,并在信号发送前将其抵消掉。

设x=[x1,… ,xN]T，u=[u1,… ,uN]T，n=[n1,… ,nN]T分别为载体(或其变换域系数)、PN序列及攻击噪声的列向量表示，长度均为N(N为SS增益)，其中u中的元素取值为+σu或-σu(σu为噪音方差)。待嵌入的信息比特映射为双极性，记作b=±1。嵌入信息后的信号和接收到的信号分别记作s与y，在加性攻击信道下y=s+n。

式中，(y,u)≈yTu/N(Tu为嵌入载体u的矩阵转置)为向量内积。假定向量x和n中的各元素独立，均服从零均值的高斯分布。

载体与噪声具有相同的行为，而载体功率通常远大于隐藏信息和噪声。因此，传统SS中载体对隐藏信息构成强干扰，从而严重限制了系统的性能，甚至在没有攻击的情况下也无法实现零误码。ISS在信息嵌入端利用已知载体信息补偿载体对信息解码的干扰，其嵌入过程可描述为

式中：a和λ为对控制信息的嵌入失真和载体对伪装信息解码干扰程度的表示；x为载体在PN序列上的投影，亦即接收端的载体干扰量。ISS信息的平均嵌入失真E(D)为

在高斯分布假设下，判决变量也服从高斯分布：

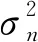
式中，Q()为正交幅度调制函数。特别地，当λ=0时，ISS退化为SS；当λ=1时，载体干扰被完全抵消，此时BER为

从式(1)到式(6)，当λ=1时，ISS方案的判决变量不包含载体项，故在相同条件下ISS方案的BER比SS方案低得多(通常低若干个数量级)。当无攻击噪声时，可以完整无误地恢复嵌入的信息。另外，与SS方案相比，ISS方案在伪装信息编码端仅增加了一项补偿信号的计算，复杂度低，而解码端与SS方案相同。ISS方案保留了SS方案对信号增益不敏感的特性，使其比量化方案更适合应用于音频伪装或信息隐藏。

1.2 扩展的ISS

本文将ISS方案扩展至接收端非匹配滤波的情况，称为扩展的ISS。令向量ut和u分别为发送端预处理后的序列和接收端的参考序列(即PN序列)。在接收端非匹配滤波的情况下，ut≠u，且ut无法从接收信号中精确恢复。此时，将式(2)的信息嵌入过程修正为

在接收端，以参考序列u对接收信号y=s+n作互相关，得到判决变量r为

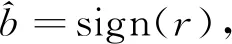
2 利用边信息的SS音频伪装方案

2.1 伪装信息的嵌入及提取

2.1.1 利用边信息的伪装信息嵌入

信息嵌入端包括基于心理声学模型的信息整形与扩展的ISS两个模块，如图1(a)中的虚线框所示，其边信息输入用粗箭头表示。嵌入过程如下：

图1 利用边信息的SS音频伪装方案

(1) 信息序列生成

根据密钥生成一个PN序列u，经过频域和时域整形得到不可感知的序列up。

(2) 载体干扰计算

将载体音频x与up分别通过高通滤波器，滤波算法以线性映射F(·)表示。然后计算载体干扰量：

由于人耳对低频失真更为敏感，故低频中的伪装相对于音频应具有更低的功率以满足感知透明度的要求，即低频段的伪装信息功率比(Standing Wave Ratio，SWR)通常高于其他频段。对音频及伪装信息进行高通滤波后，由于滤除了SWR较高的频段，整体上音频载体的功率衰减比伪装信息更为显著，则式(9)中F(x)与F(up)的功率比(即高通滤波后的SWR)小于x与up的功率比，故载体干扰量x被削弱，从而减小了载体干扰补偿信号带来的额外失真。选择高通滤波器的截止频率时应使其充分削弱音频载体的功率(通常集中在0～4 kHz)，同时保留足够的伪装信息带宽以对抗低通类的攻击(如低通滤波和重采样等)。实验确定截止频率的经验值为3～4 kHz。由于SS方案具有很宽的伪装信息频谱，因而对轻微的带宽误差不敏感，故下文中以4 kHz为例进行仿真和测试。在传输带宽远大于信号带宽条件下进行SS加密，实际环境能正常支持。

(3) 调制

采用扩展的ISS，得到包含伪装信息的音频信号：

2.1.2 伪装信息的盲提取

伪装信息盲提取方案如图1(b)所示。接收到的音频信号y=s+n首先经过与嵌入端相同的高通滤波器F(·)，再与根据同一密钥产生的参考序列u进行相关运算，得到判决变量：

2.2 参数设计

2.2.1 帧长

帧长即PN序列的长度N，也称为SS增益，可用于在信息鲁棒性与速率之间进行折中。基于SS的音频伪装系统每个声道的信息速率可表示为fs/N，fs为音频采样率。N越大则信息鲁棒性越好，但速率越低。帧长的另一个影响是信息嵌入和提取的吞吐延时，N越大则缓冲和处理一帧的时间也越长，这在实时应用中尤为重要。本文所提算法复杂度较低，不会带来额外的延时。

合适的帧长还可降低接收端的计算复杂度。接收到的音频序列y与参考序列u(长度均为N)的互相关可以用快速傅里叶变换(Fast Fourier Transformation，FFT)实现快速计算，方法如下：

(1) FFT的点数L选择接近但不小于2N-1的2的整数次幂；

(2) 将序列u前后倒置，并取复共轭，即u*=[uN,uN-1,…,u1]*；

(3) 在序列y与u*后面补L-N个零，并分别计算L点的FFT，得到L点的复序列Y=fft()×y(fft()为FFT函数)与U=fft(u*)；

(4) 计算Y与U元素乘积的快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)，即z=ifft(Y*U) (ifft()为IFFT函数)，*为逐元素相乘；

(5) 截取序列z的前2N-1个点，即为序列y与u的互相关。

可见，当帧长N取2的整数次幂时，FFT点数L=2N与2N-1接近，采用FFT实现快速相关的优势明显，且容易进一步细分为等长的片段。

2.2.2 载体干扰控制

参数λ用于控制载体对伪装信息解码的干扰。对于λ∈(0,1]，式(10)右端第2项的载体干扰被削弱。为实现最优的载体干扰抵消性能，实验中取λ=1。

2.2.3 嵌入失真控制

假定经过整形的信息序列up恰好满足不可感知的要求，则整体的嵌入失真在任何时刻都不应超过叠加up造成的失真。

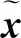
图2 高通滤波前后载体投影的概率分布

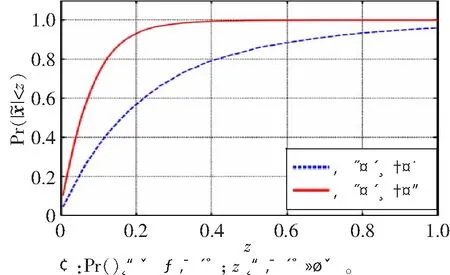
图的累积分布函数

图4 概率随的变化

2.3 性能评估

音频载体选用附录中的100段44.1 kHz采样的立体声片段，各持续10 s。测试上述算法的透明度、速率和鲁棒性等指标及其对参数的敏感性，并与现有方案进行对比。

设置以下两组参数，分别测试载体干扰抵消技术的优势：

(1)λ=0,a=0.52，即不抵消载体干扰(退化为传统SS)；

(2)λ=1,a=0.5，即完全抵消载体干扰。

帧长N均取8 192，在44.1 kHz 采样率下伪装信息速率为5.38 bit/s/channel。由于抵消载体干扰将造成额外的嵌入失真，故第2组参数中的a略小于第1组，从而使二者音质相当。测得两组参数下信号—伪装信息SWR、客观差异等级(Objective Difference Grade，ODG)及无攻击时的伪装信息解码BER分别为

(1)SWR=30.0 dB，ODG=-0.31，BER=0.09%；

(2)SWR=30.2 dB，ODG=-0.31，BER=0。

可见，上述两种方案均可获得较高的音质，但传统SS方案由于受到载体的干扰，即使在无攻击的情况下也难以保证无差错地提取伪装信息；而本文提出的扩展ISS方案可以完全抵消载体干扰，从而实现无攻击时的零误码。

在相同的音质及信息速率条件下，测试两种方案对抗信号处理和攻击的鲁棒性。以常见的加性高斯白噪声信道和连续图像/电影格式中的声音部分(MPEGAudioLayer3，MP3)压缩为例，信息提取的BER如图5所示。其他类型的攻击也具有类似的趋势。由图可知，与传统SS方案相比，本文所提方案利用边信息的载体干扰控制技术，能够在相同信息透明度与速率条件下获得更高的鲁棒性。

图5 对不同的λ，典型攻击下伪装信息解码的BER(N=8 192)

3 结束语

本文研究了SS中利用嵌入端的边信息减小伪装信息与载体相互干扰的关键技术，在限制伪装信息对载体的干扰(即嵌入失真)方面，本文提出了一种利用边信息对伪装信息进行频域与时域联合整形的方案。该方案提供了较高的和可调节的输出音质，从而保证了音频伪装方案的透明度。在限制载体对伪装信息的干扰方面，扩展了ISS在收、发序列不匹配时的嵌入方法，在信息嵌入端利用载体边信息补偿和抵消了其在接收端对伪装信息解码的干扰，改善了SS音频伪装的鲁棒性，在无攻击时可实现零误码。