有限矩形板基于权函数法的应力强度因子计算

陈 昊，董登科

(中国航空工业集团有限公司 中国飞机强度研究所，陕西 西安 710065)

1 引 言

飞机在使用过程中，其材料和结构会因为各种原因而产生裂纹缺陷。裂纹在载荷和环境条件的共同作用下不断扩展，最终会导致结构断裂，引发严重的后果。因此，对含裂纹材料和结构进行研究对于航空工业具有重要的意义。

基于断裂力学的基本理论对线弹性裂纹尖端场的分析表明，所有影响裂纹尖端力学状态的变量，仅通过应力强度因子K来影响裂纹体的行为。一旦K确定，裂纹尖端区内的应力应变和位移分量也随之确定。鉴于K在裂纹问题分析中的核心地位，各种裂纹体在任意载荷下K的求解成为断裂力学中非常重要的研究内容。

许多学者对应力强度因子的求解方法进行了深入的研究。Wu等建立了基于裂纹面位移的规范化解析权函数法[1]和Glinka-Shen基于两种(或三种)参考载荷和一个几何条件的通用权函数法[4]，并结合有限元软件ANSYS计算应力强度因子的权函数。

2 权函数法

权函数法是一种通用性很强、效率很高的应力强度因子求解方法。因为权函数把载荷条件和几何条件分开考虑，只包含裂纹体几何特征，不受载荷影响。因此，一旦确定了权函数m(a,x)，就可以计算不同裂纹尺寸在不同载荷下的应力强度因子，并且一次计算就能够得到一种载荷情况下一条完整的K(a)曲线，而有限元等数值方法一次计算只能得到一个特定裂纹长度a下的K值。

含裂纹结构的应力强度因子K的计算是对权函数m(a,x)和应力分布σ(x)的乘积进行积分。此处的应力分布是未含裂纹结构在假想裂纹处的应力分布。

2.1 裂纹的权函数法

对于二维裂纹结构的应力分布形式，应力强度因子计算公式为[3]：

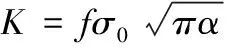
(1)

式中，α和ξ分别是无量纲的裂纹长度和坐标(a和x分别是实际裂纹长度和坐标，W是裂纹体的特征尺寸)，σ(ξ)是不考虑裂纹的存在、假想裂纹位置的应力。

断裂力学中，权函数求解法最早由Bueckner提出，Rice对其做了进一步的研究。高精度权函数的推导与验证是采用权函数法处理裂纹问题的关键。本文二维裂纹的权函数推导方法主要为：基于裂纹面位移的规范化解析权函数法和基于多个参考载荷情况的权函数法。

2.1.1 基于裂纹面位移的规范化解析权函数法

Wu等建立了基于裂纹面位移的规范化解析权函数法，对裂纹在一种参考载荷情况下的裂纹面位移分别提出了规范化的级数展开表达式[3]。利用裂纹尖端场的特性、自洽条件、裂纹嘴位移和合理的几何条件及其各种组合，推导位移级数的相关函数，进而由裂纹面位移对裂纹长度求偏导数，确定裂纹权函数m(α,ξ/α)中的系数βi(α)。

对于中心裂纹，该解析权函数的通式为：

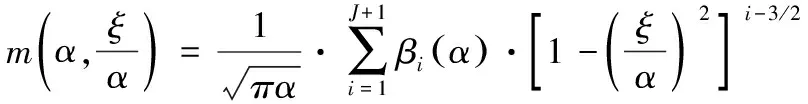
(2)

(3)

对于边缘裂纹，该解析权函数的通式为：

(4)

(5)

式中，Fi(α)为裂纹面位移展开级数的系数。

2.1.2 基于多个参考载荷情况的权函数法

考虑到早期基于裂纹张开位移的P-A方法在求解精度和适用范围方面的缺陷以及在权函数的获取过程中所需数值积分的麻烦，一些研究者改用其他方法，即利用多个参考载荷情况的已知K解来推导权函数。

Glinka和Shen确立了一种适用于所有裂纹几何的通用权函数法[5]，该权函数的确定是基于两个或三个参考载荷情况及相关几何条件，其通用权函数基本公式为：

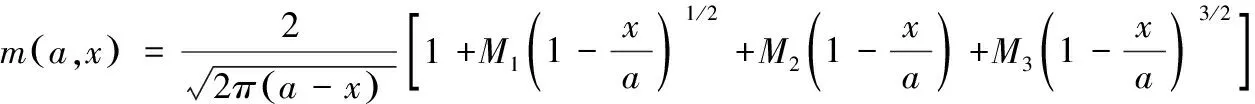
(6)

式中，系数M1、M2、M3需要基于两种(或三种)载荷情况下的已知K解(附加几何条件)，通过求解一组联立方程确定。

上述两种权函数法都需要一个或多个参考载荷情况下的K值(及裂纹嘴位移)[7]。获得这些已知条件的途径，一是从文献中查找理论精确解或其他方法得到的高精度数值解，二是采用经过反复验证的数值方法(有限元、边界元等)计算确定。本文采用有限元计算参考载荷下的应力强度因子。

2.2 格林函数

由参考载荷情况应力强度因子导出权函数之后，结合给定应力分布下的应力强度因子，并与其他方法得出的应力强度因子进行对比，是目前常用的评估应力强度因子算法准确性的一种方式。但是，这种方法实际上并不能很准确地反映权函数的精度，因为由权函数法计算应力强度因子，在导出权函数后，需要对权函数m(a，x)和无裂纹体假想裂纹处的应力σ(x)的乘积沿整个裂纹面做积分，而积分具有平均效应，所以由积分得到的应力强度因子不能真实反映权函数这一参数本身的精确性。当应力分布沿裂纹面剧烈变化，尤其当应力方向改变时，应力强度因子的误差甚至可能会远大于权函数本身的误差。因此，评价权函数算法精度的更好的方法是针对不同裂纹长度，沿着裂纹面逐点对权函数进行比较，即比较格林函数[8]。这种比较方式不会受权函数与应力乘积的积分平均效应的影响。

格林函数G(a，x)又称为影响函数[9]，表示裂纹面在任意位置受到一对单位集中力P作用时的无量纲应力强度因子。格林函数G(a，x)与裂纹面受一对单位集中力P作用下的应力强度因子K沿着集中力作用的位置逐点对应，其与权函数的关系如下：

(7)

3 有限矩形板裂纹应力强度因子计算

对于平板结构，工程上常见的裂纹形式为中心裂纹和边缘裂纹。很多学者提出了各种求解权函数的方法，本文分别采用基于裂纹面位移的规范化解析权函数法和基于多个参考载荷条件的Glinka-Shen通用权函数法计算有限矩形板中心裂纹和边缘裂纹的应力强度因子。

3.1 基于裂纹面位移的规范化解析权函数法

3.1.1 有限矩形板中心裂纹问题

考虑有限矩形板中心裂纹问题，板宽度为2W、长度为2H，裂纹长度为2a(有限矩形板中心裂纹如图1所示)。选取板半宽W作为该裂纹几何特征尺寸，无量纲裂纹长度α和坐标ξ分别为：α=a/W,ξ=x/W。

图1 有限矩形板中心裂纹

选取裂纹面均布应力作为推导中心裂纹权函数的参考载荷。对于裂纹面受均布应力的中心裂纹，α=0时，应力强度因子和裂纹嘴位移都存在理论精确解；α=1时，应力强度因子存在理论极限值。

α=0时：

fr(0)=1Vr(0)=2.0

α=1时：

(8)

对于有限矩形板中心裂纹，本文利用有限元软件ANSYS19.0建立模型，模拟不同裂纹长度的中心裂纹，并进行应力分析。模拟裂纹长度α包括0.01、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9共11个模型。

为了简化计算，提高运行效率，本文建立1/4模型，并施加对称边界条件。裂纹尖端处采用1/4节点奇异单元，网格类型设置单元PLANE183，裂纹尖端网格如图2所示。材料属性：杨氏模量E=7.17×105MPa，泊松比v=0.3。

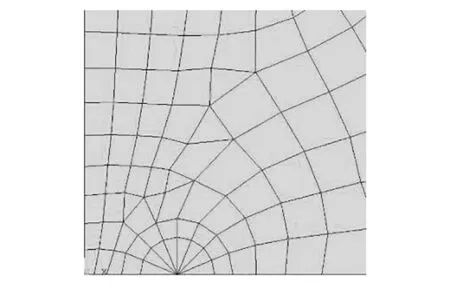
图2 裂纹尖端网格

利用ANSYS进行应力强度因子Kr和裂纹嘴位移Ur计算，结果如表1所示。

表1 有限元计算结果

根据有限元计算得到的Kr和Ur值，采用式(9)对其进行正则化处理，得到无量纲应力强度因子fr(α)和无量纲裂纹嘴张开位移Vr(α)，然后再通过多项式拟合，得到fr(α)和Vr(α)的高精度拟合多项式。

Vr(α)=ur(α,ξ=0)E′/(σ0α)

(9)

(10)

式中的多项式系数λi和γn如表2所示。

表2 均布应力下fr(α)和Vr(α)的多项式系数

把fr(α)和Vr(α)的高精度拟合多项式代入式(11)，可以方便地求得Ø(α)的积分式。将其代入式(3)，就能确定裂纹面位移函数中的Fj(α)，j=1～3。

(11)

再将Fj(α)代入式(2)，便能确定βi(α)的值。对βi(α)的计算结果进行多项式拟合，得到有限矩形板中心裂纹βi(α)的多项式拟合表达式：

β1=2

β2=(-26.32α7+90.14α6-126.2α5+91.83α4-38.16α3+9.297α2-0.5675α-0.0001263)/(1-α)＾1.5)

β3=(17.49α7-90.07α6+164.4α5-144.4α4+65.71α3-14.97α2+1.378α-0.0002538)/(1-α)＾1.5)

β4=(19.82α7-33.51α6+1.365α5+29.83α4-23.12α3+6.86α2-0.7436α+0.000396)/(1-α)＾1.5)

(12)

把所求的βi(α)代入下式，就能确定有限矩形板中心裂纹的解析权函数。

3.1.2 有限矩形板边缘裂纹问题

考虑有限矩形板边缘裂纹问题，板宽度为W、长度为H，裂纹长度为a(有限矩形板边缘裂纹如图3所示)。选取板宽W作为该裂纹几何特征尺寸，无量纲裂纹长度α和坐标ξ分别为：α=a/W，ξ=x/W。

图3 有限矩形板边缘裂纹

选取裂纹面均布应力作为推导边缘裂纹权函数的参考载荷。对于裂纹面受均布应力的边缘裂纹，α=0时，应力强度因子和裂纹嘴位移都存在理论精确解；α=1时，应力强度因子存在理论极限值。

α=0时：

fr(0)=1.1215

Vr(0)=2.9086

α=1时：

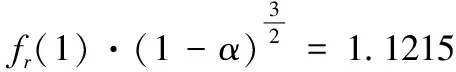
(14)

对于有限矩形板边缘裂纹，本文利用有限元软件ANSYS19.0建立模型，模拟不同裂纹长度的边缘裂纹，并进行应力分析。模拟裂纹长度α包括0.01、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9共11个模型。

为了简化计算，提高运行效率，本文建立1/2模型，并施加对称边界条件。裂纹尖端处采用1/4节点奇异单元，网格类型设置单元PLANE183。材料属性：杨氏模量E=7.17×105MPa，泊松比v=0.3。

利用ANSYS进行应力强度因子Kr和裂纹嘴位移Ur计算，结果如表3所示。

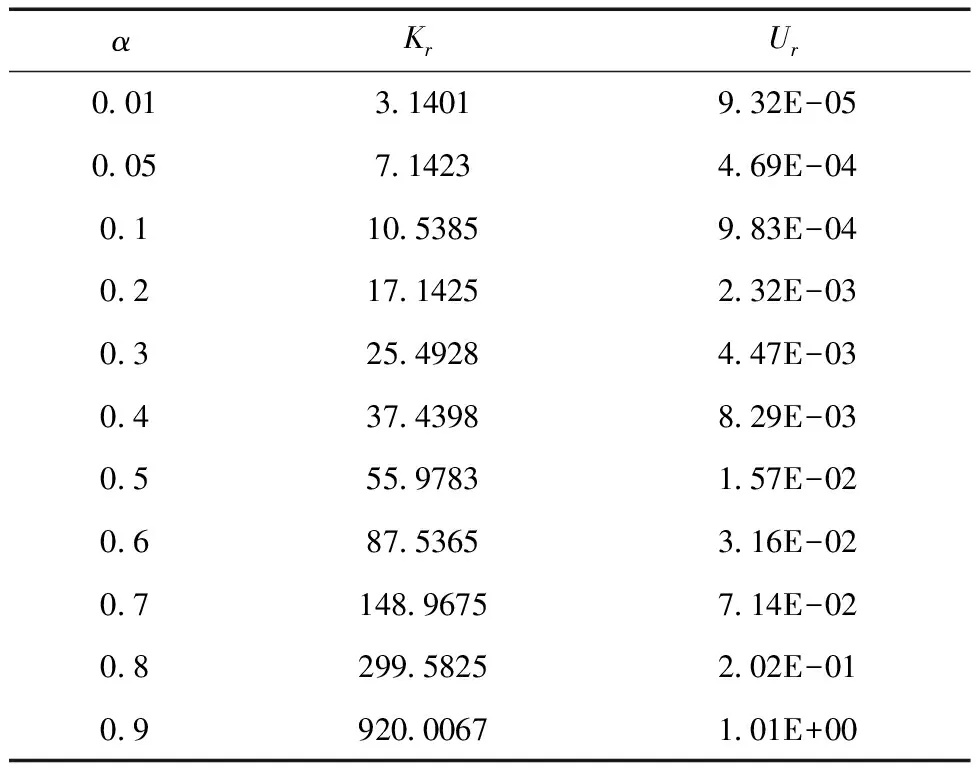
表3 有限元计算结果

根据有限元计算得到的Kr和Ur值，根据式(15)对其进行正则化处理，得到无量纲应力强度因子fr(α)和无量纲裂纹嘴张开位移Vr(α)，然后再通过多项式拟合，得到fr(α)和Vr(α)的高精度拟合多项式。

(15)

式中的多项式系数λi和γn如表4所示。

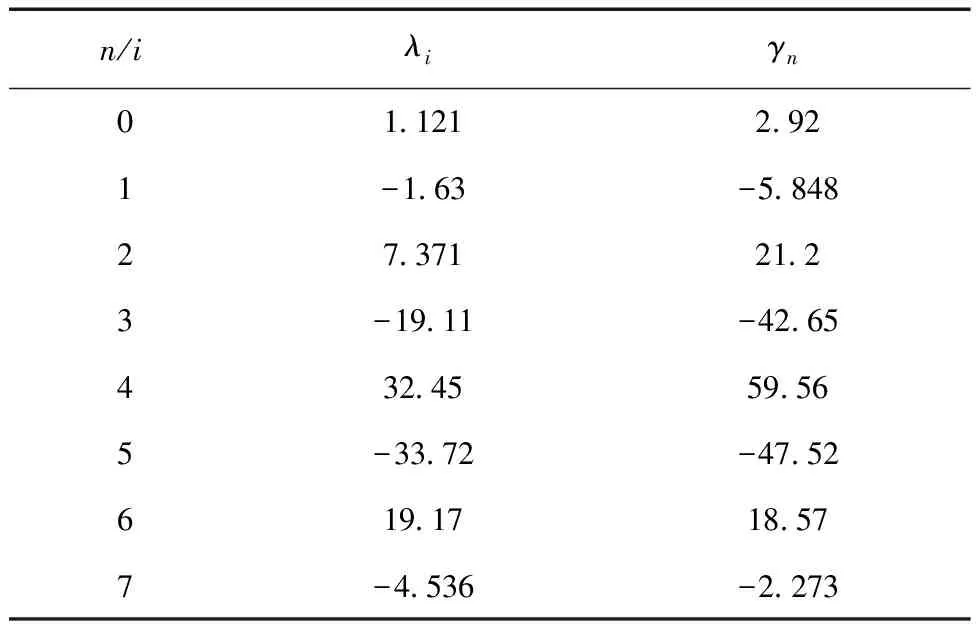
表4 均布应力下fr(α)和Vr(α)的多项式系数

把fr(α)和Vr(α)的高精度拟合多项式代入公式，可以方便地求得Ø(α)的积分式。将其代入式(4)，就能确定裂纹面位移函数中的Fj(α),j=1～3。再将Fj(α)代入式(5)，便能确定βi(α)的值。对βi(α)的计算结果进行多项式拟合，得到有限矩形板边缘裂纹βi(α)的多项式拟合表达式：

β1=2
β2=-68.01α7+208.4α6-274.4α5+205α4-105.1α3+32.42α2+1.568α+0.845
β3=246α7-668.3α6+697α5-316.4α4+44.01α3+23.32α2-9.025α+1.573
β4=-364.4α7+1065α6-1230α5+675.1α4-166.7α3+3.357α2+5.667α-0.786
β5=133α7-392.7α6+459.1α5-256.2α4+64.59α3-2.57α2-1.353α+0.05477

(16)

把所求的βi(α)代入下式，就能确定有限矩形板边缘裂纹的解析权函数。

3.2 基于多个参考载荷条件的Glinka-Shen通用权函数法

本文求解权函数的另一种方法是基于多个参考载荷条件的Glinka-Shen通用权函数法。

3.2.1 有限矩形板中心裂纹问题

对于有限矩形板中心裂纹，选取均布应力、线性应力、二次应力作为推导中心裂纹权函数的参考载荷。

均布应力：σ(x)=1

线性应力：σ(x)=(1-x/a)

二次应力：σ(x)=(1-x/a)2

(18)

本文利用有限元软件ANSYS19.0建立矩形板有限元模型，模拟不同应力条件下不同裂纹长度的中心裂纹，并进行应力分析。模拟裂纹长度α包括0.01、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9共11个模型。

为了简化计算，提高运行效率，本文建立1/4模型，并施加对称边界条件。在裂纹尖端处采用1/4节点奇异单元，其余网格类型设置为单元PLANE183。材料属性：杨氏模量E=7.17×105MPa，泊松比v=0.3。

利用ANSYS进行应力强度因子Kr和裂纹嘴位移Ur计算，结果如表5所示。

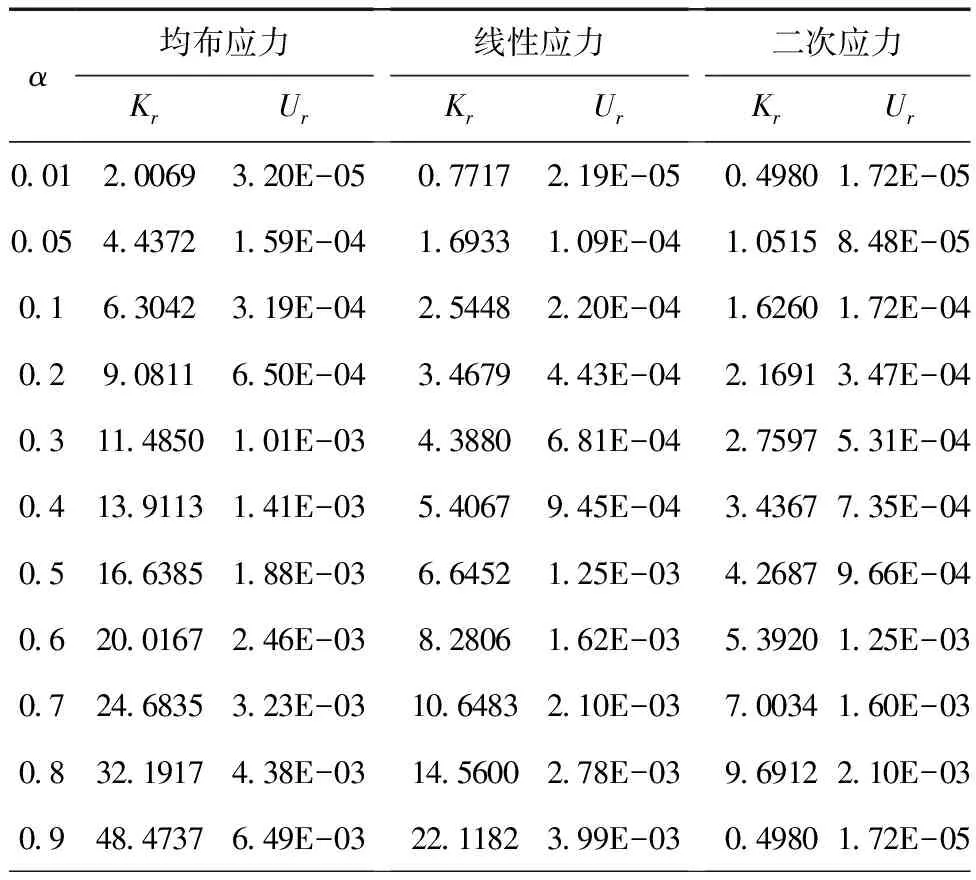
表5 应力强度因子Kr和裂纹嘴位移Ur的有限元计算结果

将通过ANSYS求解得到的不同应力分布下的应力强度因子作为参考应力强度因子和对应的应力分布函数，代入式(19)，并联立方程组，可求得不同裂纹长度对应的M1、M2、M3的值，如表6所示。

(19)

表6 不同裂纹长度对应的M1、M2、M3的数值

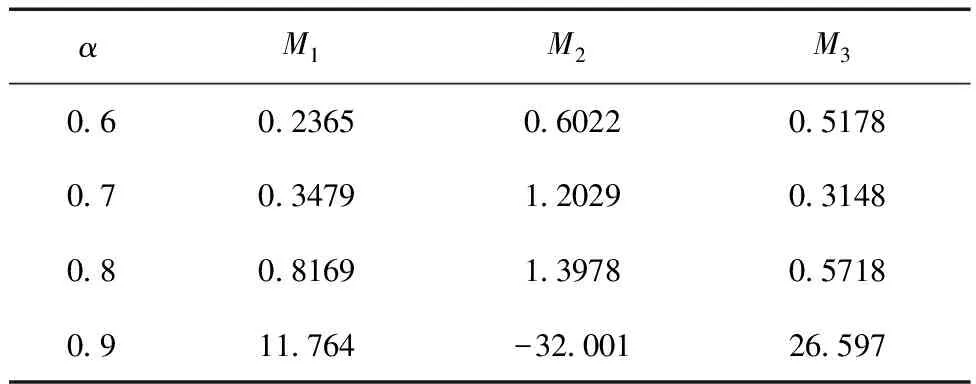
续表6

根据计算得到的M1、M2、M3的值，对其进行正则化处理，然后再通过多项式拟合，得到M1、M2、M3的高精度拟合多项式：

M1=0.7752α8+0.1064α7-0.7361α6-1.112α5-0.6818α4+1.542α3+0.06072α2+0.6471α-0.2981
M2=-4.281α8+1.314α7+8.549α6-1.274α5-4.031α4-0.2923α3+2.151α2-2.121α+1.52
M3=4.24α8-1.959α7-10.1α6+4.009α5+7.003α4-2.499α3-2.462α2+2.46α-0.4551

(20)

把所求得的M1、M2、M3的拟合多项式代入下式，就能确定有限矩形板中心裂纹的解析权函数，可求解对应载荷作用下的应力强度因子。

(21)

3.2.2 有限矩形板边缘裂纹问题

对于有限矩形板边缘裂纹，选取均布应力、线性应力、二次应力作为推导边缘裂纹权函数的参考载荷。本文利用有限元软件ANSYS19.0建立有限矩形板的有限元模型，模拟不同应力条件下不同裂纹长度的边缘裂纹，并进行应力分析。模拟的裂纹长度α包括0.01、0.05、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9共11个模型。

为了简化计算，提高运行效率，本文建立1/2模型，并施加对称边界条件。在裂纹尖端处采用1/2节点奇异单元，其余网格类型设置为单元PLANE183。有限元模型的材料属性：杨氏模量E=7.17×105MPa，泊松比v=0.3。

利用ANSYS进行应力强度因子Kr和裂纹嘴位移Ur计算，结果如表7所示。

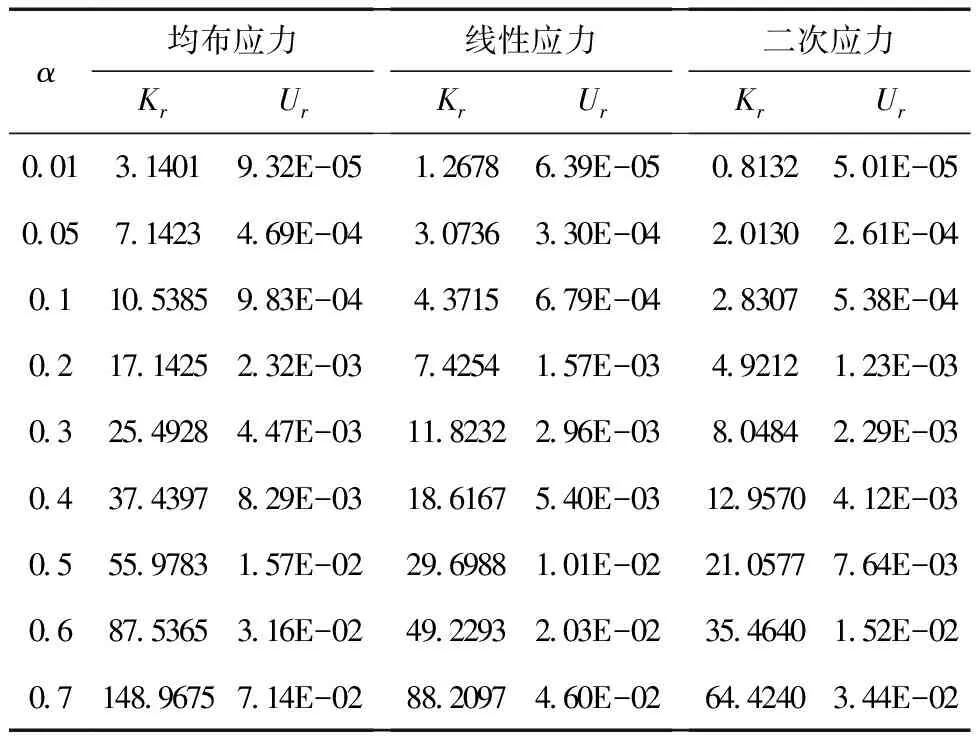
表7 应力强度因子Kr和裂纹嘴位移Ur的有限元计算结果

续表7

将通过ANSYS求解得到的不同应力分布下的应力强度因子作为参考应力强度因子和对应的应力分布函数，代入式(19)，并联立方程组，可求得不同裂纹长度对应的M1、M2、M3的值，如表8所示。

表8 不同裂纹长度对应的M1、M2、M3的数值

根据计算得到的M1、M2、M3的值，对其进行正则化处理，然后再通过多项式拟合，得到M1、M2、M3的高精度拟合多项式。

M1=-0.1514α8+0.005979α7+1.767α6+1.647α5-1.11α4-0.04461α3+1.221α2+2.335α+1.619

M2=0.868α8+0.05433α7-7.228α6-5.851α5+4.987α4+0.8334α3-3.057α2-4.74α-2.548

M3=2.115α8+4.88α7+1.841α6-2.226α5+1.432α4+7.806α3+7.94α2+10.53α+6.98

(22)

把所求得的M1、M2、M3的拟合多项式代入公式，就能确定有限矩形板边缘裂纹的解析权函数，可求解对应载荷作用下的应力强度因子。

4 权函数精度评价

格林函数G(a,ξ/α)又称为影响函数，表示裂纹面在任意位置受到一对集中力P作用时的无量纲应力强度因子。

4.1 中心裂纹的格林函数

在有限矩形板中心裂纹的裂纹面任意位置处施加一对集中力P(单位厚度)，计算格林函数并绘制函数的图像，如图4所示。

(23)

图4 中心裂纹的格林函数

4.2 边缘裂纹的格林函数

在有限矩形板边缘裂纹的裂纹面任意位置处施加一对集中力P(单位厚度)，计算格林函数并绘制函数的图像，如图5所示。

(24)

图5 边缘裂纹的格林函数

5 结 论

本文通过不同的权函数法计算有限矩形板中心裂纹和边缘裂纹的权函数，主要内容如下：

(1)基于裂纹面位移的规范化解析权函数法，是通过参考载荷下的裂纹面位移Ur(a,x)对裂纹长度a求偏导数推导确定。

(2)使用ANSYS计算参考应力强度因子，确定权函数的关键一步是求得参考载荷情况下的高精度裂纹张开位移Ur(a,x)，然后得到权函数的解析表达式m(α,ξ)。

(3)基于Glinka-Shen通用权函数法采用三个参考应力计算相应的参考应力强度因子，计算权函数中的待定参数M1、M2、M3，最终确定应力强度因子的权函数。

(4)采用格林函数验证了所求权函数的正确性，为飞机结构和材料的应力强度因子确定、疲劳裂纹扩展预测提供了一种简便、高效的方法。