科技辅助实验教学 促进学生深度学习①——以“实验：探究平抛运动的特点”教学为例

丁 松 郑宏伟 方 晨

(江苏省清江中学，江苏 淮安 223001)

比较人教社2004年出版的物理必修2中“实验：研究平抛运动”与2019年出版的物理必修第二册中“实验：探究平抛运动的特点”，[1-2]2019年版教材把平抛运动的实验放在“抛体运动的规律”之前，突出了探究性实验的重要性。2019年版教材中实验强调的是“探究”，2004年版教材实验突出的是“验证”。《普通高中物理课程标准(2017年版)》将“探究平抛运动的特点”定为学生必做实验之一。本教学设计兼顾了新教材中探究的实验目的和旧教材中验证平抛运动轨迹为抛物线的实验目的。

1 实验方案设计创新

1.1 实验器材和软件

“自编软件”(自动获取运动物体的轨迹及相关坐标)、实心球、电脑、智能手机以及支架(拍摄视频用)、希沃授课助手(学生数据处理的实时投屏)等。

利用自编软件可获取生活中的抛体运动的相关数据，经过数据处理后学生可自主得出结论：平抛物体在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，且可求出重力加速度g。用实验同时探究出了平抛运动在水平方向上和竖直方向上的规律，这一点比教材上设计的相关实验方案更优越。

1.2 实验操作步骤

① 将里面注满沙子的网球从离地面高度约为1.5米的桌边(桌面事先已经用水平仪调节水平)水平抛出，利用手机的摄像功能记录这一运动过程(图1)。

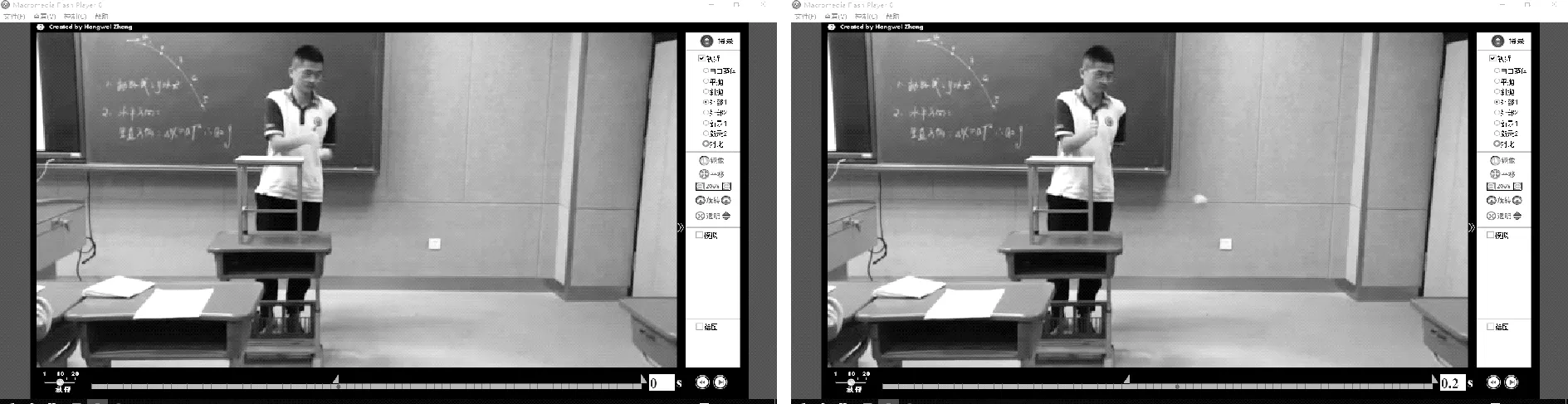
图1

② 然后对这段视频进行处理，每隔相等的时间截取1帧画面，共30帧，并导入自编软件进行处理，通过调节，使实际小球的运动轨迹与软件中的模拟小球运动轨帧迹重合、步调一致。

③ 点开软件中的“坐标纸功能”，就可以实时读出每一帧图片中小球的坐标。如图2所示，为每隔2帧读取一次小球的坐标，因为视频为每秒30帧，所以是每隔Δt=0.1 s 读取一次小球的坐标。

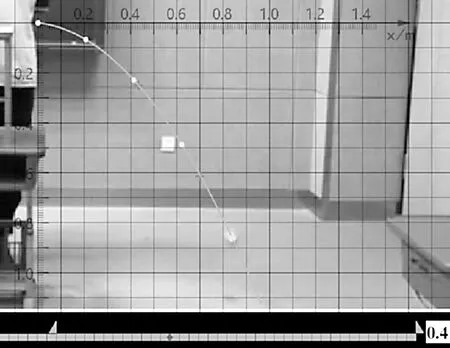
图2

1.3 实验误差分析

① 模拟曲线与实际平抛运动曲线无法完全重合且同步，所以在模拟运动过程中，总会有误差。例如，同一个平抛运动，经过几次的模拟，同一个点的坐标会略有不同。

② 在相机拍摄的每一帧图片中，小球的图像由于延时曝光形成了轻微的拖影，会影响坐标的精确性。

③ 拍摄的视频由于视角问题，导致手机镜头不可能在小球的整个运动过程始终与小球相平行，会导致小球的实际运动和视频中小球的运动略有差别。

2 实验数据处理创新

将“数据计算”交给平板电脑，将“创造性的劳动——实验方案设计以及实验器材操作”交给学生，然后观察表格中灰色区域的数据，从而总结平抛运动的规律。

表1说明：视频已经转换成30帧，每隔2帧(间隔为0.1 s)取一个坐标，从中可以发现：相同时间内水平位移相同，相邻相同时间内竖直位移之差为定值。根据时间间隔可很容易求出水平速度和竖直方向上的加速度g。

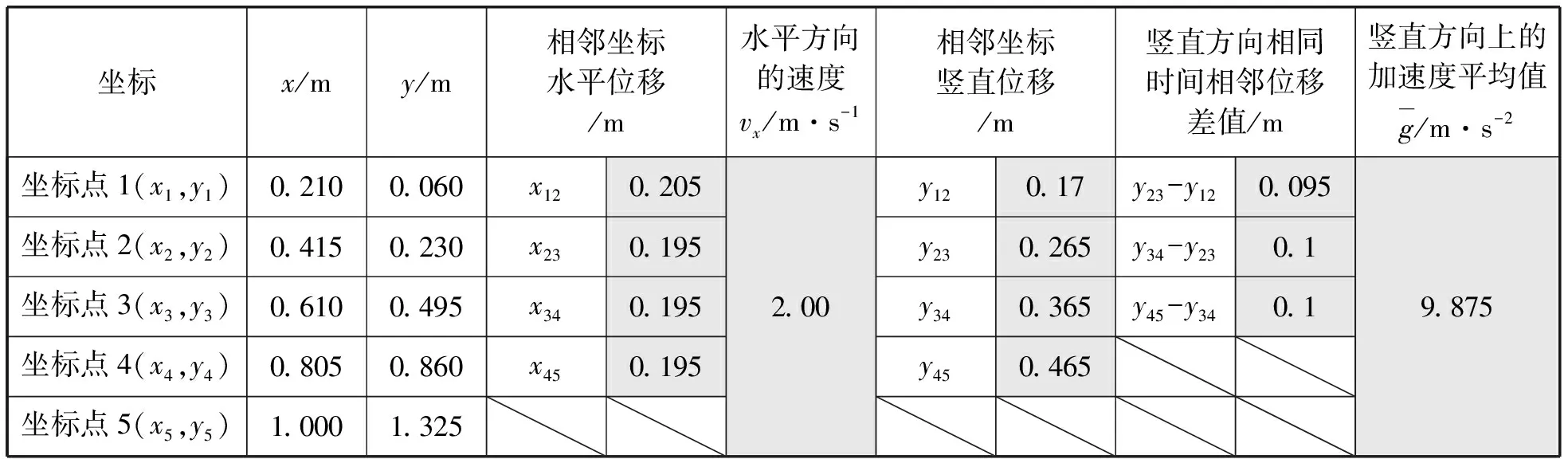
表1 利用软件处理平抛运动相关数据(验证水平、竖直方向上的运动特点)

表2说明：由于初速度相同的平抛运动和抛物线都具有对称性(图3)。我们假设抛出点为抛物线的顶点，所以我们只要验证坐标都满足：y=kx2。从y与x2的图像(图4)可以看出，y与x2成正比，即轨迹为抛物线。

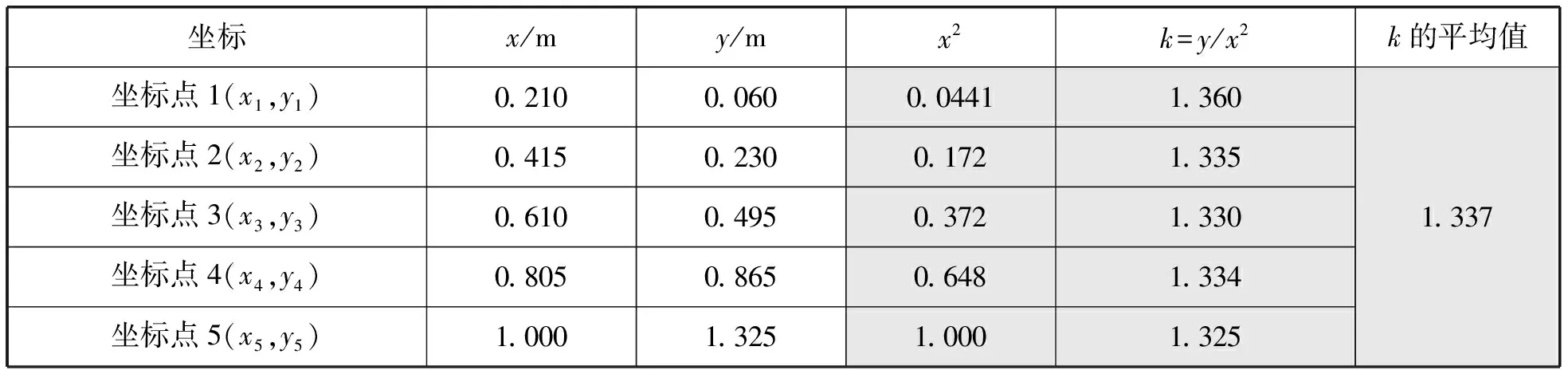
表2 平抛运动相关数据处理(验证轨迹是否为抛物线)

图3

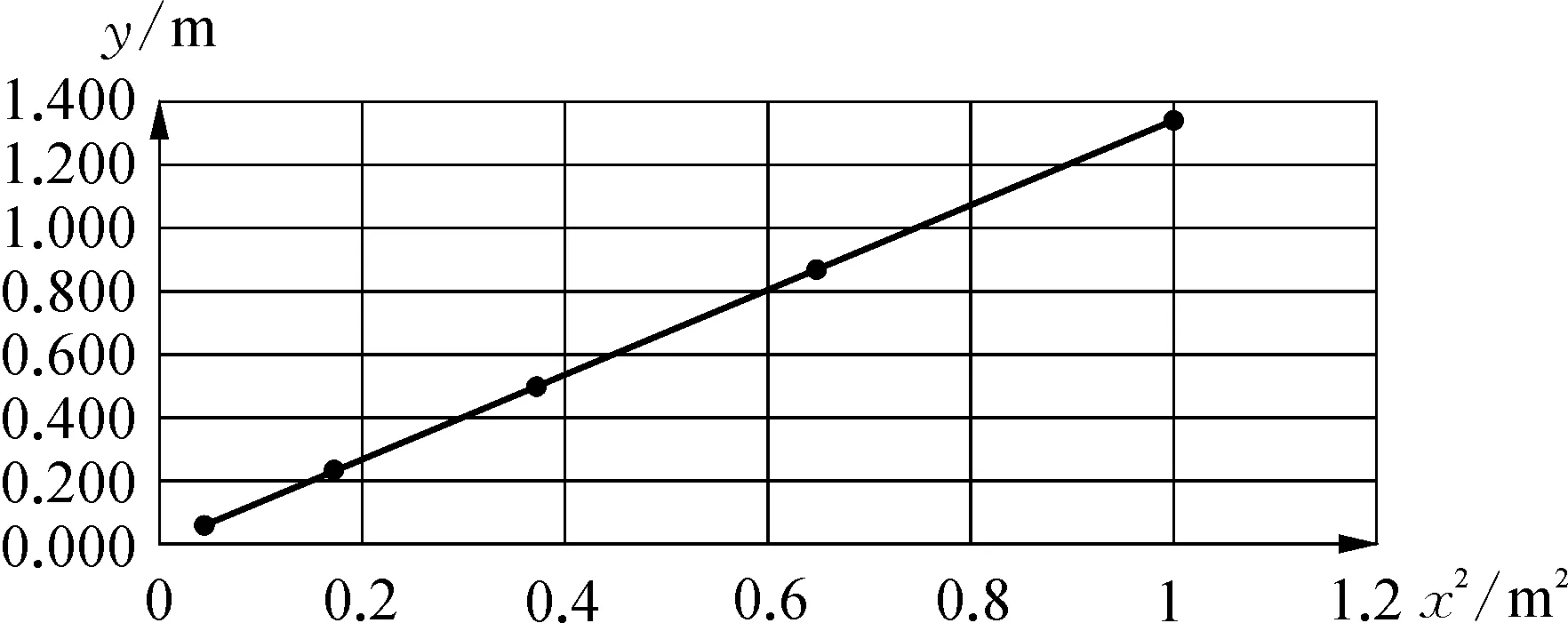
图4

3 小结

笔者研读新课标，对新教材和旧教材进行比较，获取各自的长处，引导学生深度学习，设计实验研究平抛运动的规律，培养学生科学探究能力，促进学生核心素养的发展。

美国卡布里洛大学道格拉斯·布朗教授开发的Tracker软件是OPS项目中的一个很重要的开源软件。该软件突破了以往视频只能播放不能分析的限制,它可以自动跟踪视频中的特定目标,捕捉其位置、速度和加速度等数据,并内置了统计及拟合等相关数据分析功能,很多物理专业期刊介绍了此软件的优点。[3-5]在这里主要谈谈自编软件相对于Tracker软件在使用中所具有的优势。

(1)误差对比：如果自编程序软件导入的视频中物体的实际运动轨迹和模拟小球的轨迹完全重合，并且所有的数据计算尽量精确，那么此实验几乎没有误差。自编程序软件抓住主要矛盾，忽略次要矛盾，使实验更直观、更精确。但是使用Tracker软件时，误差来源很多，不容易控制。

(2)笔者自编软件的界面交互性比Tracker软件更简洁明了。使用者可以编辑自己需要的数据，把不需要的数据去掉。例如本实验中只需要物体的某一位置的坐标(x,y)，其他的数据都可以隐去，让界面简洁明了。

(3)使用自编软件核心程序的注意点：真实视频的播放和自编程序软件中的模拟动画播放的帧数必须为每秒30帧。