基于时间相依地震活动性模型的地震时间序列模拟

徐伟进， 吴健， 李雪婧， 高孟潭

1 中国地震局地球物理研究所， 北京 100081 2 中国地震灾害防御中心， 北京 100029

0 引言

传统概率地震危险性分析方法主要是基于震源模型、地震活动性模型、地震动预测模型以及场地条件等来计算地震动影响场，结果所表示的是所有震源对场址地震危险性的综合影响.近些年来，随着计算能力的提升，在地震危险性分析、地震灾害损失预测以及地震巨灾保险模型开发等领域，科学家和工程师们也希望采用一系列单个地震事件计算目标场址或区域的地震动影响(Ebel and Kafka, 1999; Musson, 2000; Hong and Goda, 2006; Assatourians and Atkinson, 2013; Faenza et al., 2017; Xu et al., 2021).这就需要将传统潜在震源转换成一系列的地震事件，而地震活动性模型是生成地震事件的重要基础.按照地震发生概率(指未来某一确定时间段内的地震发生概率)是否随时间变化，地震活动性模型分为两类，即时间独立(time-independent)模型和时间相依(time-dependent)模型.时间独立的地震活动性模型假设地震发生概率不随时间变化，地震的发生在时间上服从指数分布，也称为泊松模型.在传统概率地震危险性分析中，即假设地震发生在时间上是一个泊松过程(Cornell,1968; 高孟潭，1996，2015；潘华等，2013；Petersen et al., 2014).Xu等(2021)基于我国最新的地震活动性模型模拟生成了符合我国时空强分布特征的随机地震事件集，该事件集在时间上符合泊松模型.

然而，近几十年来，也有许多研究表明，一些断层上的地震活动(地震发生概率)随时间有明显的变化，呈现时间相依特性，如果使用泊松模型，可能会高估或低估某一个时间段内的地震危险性水平.研究者们使用不同地区的地震目录对地震的时间特性进行了实证研究，发现在许多情况下地震并不符合泊松模型，而时间相依模型能够更好的描述地震的时间分布特征(Utsu，1984；Nishenko and Buland，1987; Ogata and Abe，1991；Tripathi，2006).研究者们提出了诸如采用伽马(Gamma)模型、对数正态(Lognormal)模型、威布尔(Weibull)模型以及布朗过程时间(Brownian Passage Time，BPT)模型来描述地震的时间分布特征(Utsu，1984；Matthews et al.，2002；Tripathi，2006；Field and Jordan, 2015；Pasari and Dikshit，2015，2018).这些模型为地震预测和地震危险性分析提供了重要的理论支撑.国内外许多学者和机构开展了基于时间相依地震活动性模型的地震发生概率和地震危险性分析(WGCEP, 1988, 1990,1995, 2003, 2007；闻学泽,1998; 杨明和刘百篪，2000；冉洪流，2006; Field et al.，2015).

由于大地震时间相依的地震活动性特征，地震发生概率是随时间变化的，未来某段时间内的地震等效发生率也会发生变化，若仍采用泊松模型进行随机地震事件的模拟，那么在足够长的时间内，得到的地震事件数量会多于或少于实际的地震事件数.由于大地震的危险性更大，这将对地震危险性分析结果产生显著影响.因此，在具有时间相依地震活动特征的断层(震源)上，应采用时间相依的地震活动性模型进行地震事件集的模拟，使模拟地震的时间序列具有时间相依特性.

具有时间相依特征的地震事件的模拟，可通过以下两种方案进行：

(1)基于地震复发间隔、复发间隔的不确定性、最近地震的离逝时间等地震活动性参数，采用时间相依的地震活动性模型计算未来某段时间内的地震发生概率，然后转换成等效地震年发生率.基于等效年发生率，仍采用泊松模型模拟地震的时间序列.该方案是将地震发生率进行了重新计算，但是地震事件的时间序列仍近似为泊松分布.目前时间相依的地震危险性分析大都是基于这一方案进行的(Petersen et al., 2007; Hebden and Stein, 2009; Field et al.，2015).

(2)基于地震复发间隔和复发间隔的标准差以及地震离逝时间，采用基于布朗随机过程的地震加卸载过程，生成具有准周期性的地震时间序列.

模拟具有时间相依特征的地震时间序列需要用到时间相依的地震活动性模型及其相关的发生概率计算，以及描述地震准周期发生的运动概率模型，将在下文中详细介绍.

1 时间相依的地震活动性模型

特征地震的发生具有准周期性，但地震发生时刻受诸多不确定性因素的影响，不会按照某个固定时间间隔精确地发生.实际情况中，特征地震的复发间隔往往具有很大的不确定性.对特征地震的描述主要集中在震级-频度分布模型和时间分布模型上.由于特征地震的震级比较固定，震级范围在0.5个震级单位内.因此，建立合适的数学模型描述特征地震的复发间隔是时间相依地震危险性分析的关键环节.目前使用较多的描述地震复发间隔的模型主要有对数正态分布模型、正态分布模型、布朗过程时间模型、伽马模型以及威布尔模型等.美国加州地震预报工作组(Working Groups on California Earthquake Probabilities，WGCEP)在1988、1990和1995年的报告中(WGCEP, 1988, 1990,1995)以及Petersen等(2007)均采用了对数正态分布模型(lognormal distribution).WGCEP在2003和2007年的报告中(WGCEP, 2003, 2007)以及Field等(2015)采用了布朗过程时间(BPT)模型.下面对BPT模型和对数正态分布模型做简要描述.

1.1 布朗过程时间(BPT)模型

Matthews等(2002)基于Reid(1910)的弹性回跳理论，并结合多个其他物理参数，提出了地震复发的BPT模型.该模型假设发震断层以恒定的加载速率进行加载，采用标准布朗运动来描述累积加载过程.在实际使用中，模型的均值和标准偏差可直接采用特征地震序列计算得到.BPT模型在理论上反映了地震孕育和发生的内在物理机制，是近年来地震学家们广泛使用的模型.BPT模型的概率密度函数可表示为：

(1)

式中，μ为复发间隔的均值，α=σ/μ为复发间隔的变异系数，σ为复发间隔的标准差.

BPT模型的累积概率函数为：

=Φ[u1(t)]+e2/α2Φ[-u2(t)],

(2)

其中

为标准正态分布函数的累积概率函数.图1是μ为1，α分别为0.25、0.5、1、2时BPT模型的概率密度函数和累积概率函数，可以看出α对概率密度函数的形状影响显著，在α较小时，概率密度函数几乎以均值对称分布，更接近于正态分布.在α较大时，概率密度函数曲线峰值显著向左移，与指数分布相似.

图1 BPT模型的概率密度函数(a)和累积概率函数(b)，BPT(1，α)，α=0.25, 0.5, 1, 2Fig.1 Example probability distributions for the BPT model with a mean recurrence interval (μ) of 1 and aperiodicity (α) values of 0.25, 0.5, 1 and 2(a) The probability density function (PDF) for recurrence interval; (b) The associated cumulative distributions.

1.2 对数正态分布模型

对数正态分布模型是将变量的对数值看成是正态分布，其概率密度函数为：

(3)

其中μ,σ分别为变量对数的均值和标准差.在实际计算中，我们已知的是变量的期望值E(T)和方差var(T)，那么变量对数的均值μ和方差σ2可分别用(4)(5)式计算:

(4)

(5)

图2中红色虚线为对数正态分布的概率密度函数和累积分布函数.通过与BPT的分布(图中蓝线)比较，可以看出对数正态分布和BPT分布非常相似.

图2 对数正态分布、BPT分布和指数分布的概率密度函数(a)和累积分布曲线(b)，各分布的均值为1，标准偏差为0.5(指数分布除外)Fig.2 Probability density (a) and cumulative distribution (b) functions of exponential, BPT, and lognormal models. All distributions have mean 1 and standard deviation 0.5 (except the exponential distribution)

2 时间相依模型的地震发生概率

2.1 时间相依的地震发生概率

根据上述介绍的时间相依的地震活动性模型，在已知大地震的离逝时间和大地震复发间隔及其不确定性时，可计算未来一段时间内地震发生的概率.设Te(escape time)为最近一次地震发生距今的时间，即所谓的离逝时间，那么未来ΔT时间内发生至少一次地震的条件概率为(Matthews et al., 2002)：

(6)

图3为BPT模型中，地震复发间隔为μ=3000 a，α分别为0.3、0.5和0.7时，未来50年发生地震的条件概率随离逝时间的变化曲线.可以看出随着离逝时间的增加，地震发生的概率先是缓慢增大，然后急剧升高，最后归于平缓.α对地震发生的条件概率影响显著，在离逝时间较长时，α越小概率越大，相反，在离逝时间较短时，α越大则概率越大.

图3 未来50年地震发生概率随离逝时间变化的函数曲线，BPT(3000a，α)，α=0.3, 0.5, 0.7Fig.3 50-year probability as a function of elapsed time for BPT model with a mean recurrence interval (μ) of 3000 a and aperiodicity (α) values of 0.3, 0.5 and 0.7

图4为地震复发间隔为μ=3000 a，离逝时间为1000 a时，采用BPT模型计算的在未来某一时间段内发生至少一次地震的条件概率.

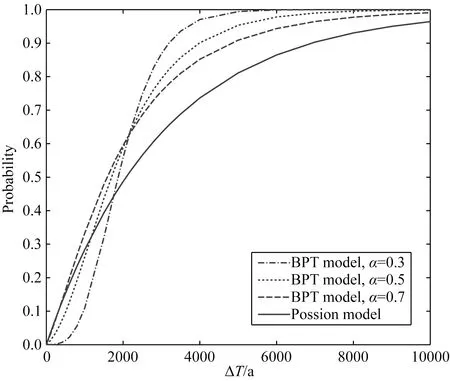
图4 未来一段时间内地震发生的BPT条件概率，BPT(3000 a，α)，α=0.3, 0.5, 0.7，T=1000 aFig.4 Probability of one or more events for the case in which the elapsed time is 1000 a for BPT model with a mean recurrence interval (μ) of 3000 a and aperiodicity (α) values of 0.3, 0.5 and 0.7

在地震学研究中，研究者们还关心某一断层上自上次发生地震以来还无地震发生的年发生概率，称为危险率(hazard rate):

(7)

图5为采用指数模型、BPT模型和对数正态模型计算的危险率随时间的变化曲线，各模型变量的均值为1，标准偏差为0.5.从图中可以看出对于指数模型，危险率不随时间变化.时间相依的危险率随离逝时间的增加有起伏变化，与泊松模型的危险率显著不同.还可看出BPT模型和对数正态模型的危险率曲线非常相似，仅在离逝时间相对很大时才有较为显著的差异.考虑到BPT模型的物理意义及其使用的广泛性，下文仅讨论基于BPT模型的地震发生概率.

图5 指数模型、对数正态分布模型和BPT模型的危险率随时间变化函数，各分布模型均值为1，标准差为0.5(指数分布除外)Fig.5 Hazard-rate functions for exponential, lognormal, and BPT models. All distributions have mean 1 and standard deviation 0.5 (except the exponential distribution)

2.2 离逝时间未知的时间相依地震发生概率计算

离逝时间是计算时间相依地震发生概率的重要参数.许多情况下，一条断层上最近一次地震的发生时间无法确定，因此计算不出具体的离逝时间.这时候需要考虑离逝时间的所有可能性.根据Field和Jordan(2015)的研究结果，离逝时间的概率分布可以用(8)式表示：

(8)

从式中可以看出离逝时间的概率密度函数为1减去地震复发间隔的累积分布函数除以平均复发间隔.

已知离逝时间的概率密度函数，结合地震发生条件概率的计算公式，基于全概率理论，对离逝时间的所有可能性进行积分，积分函数为离逝时间的概率分布乘以条件概率计算公式，具体计算公式为：

(9)

图6为离逝时间未知，采用BPT模型计算的未来一段时间地震发生的条件概率，地震复发间隔的均值μ=3000 a，α分别为0.3、0.5和0.7.α越大，采用BPT模型计算的数值越接近泊松模型，这是由于α越大，地震复发间隔的不确定性越强，越接近于泊松分布.

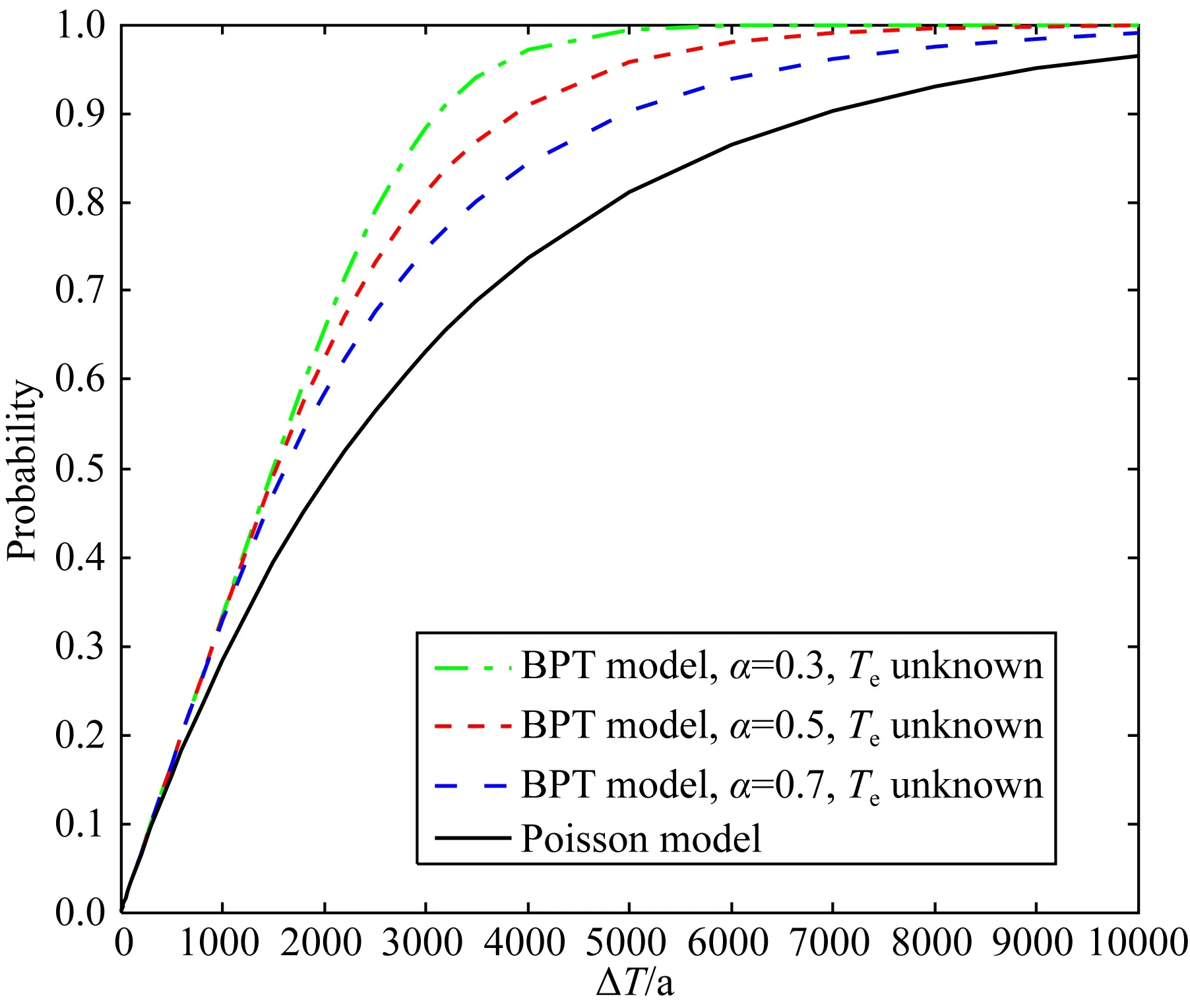
图6 离逝时间未知时采用BPT模型计算的未来一段时间至少发生一次地震的条件概率Fig.6 BPT conditional probability of one or more events for the case in which the date of the last event is unknown

图7为地震复发间隔的均值μ=3000 a，α为0.5时，采用BPT模型计算的离逝时间已知和未知情况下未来一段时间发生至少一次地震的条件概率.从图中可以看出由于离逝时间未知情况下是考虑了离逝时间的所有情况，因此计算的条件概率要大于离逝时间较小时的值，而小于离逝时间较大时的值.

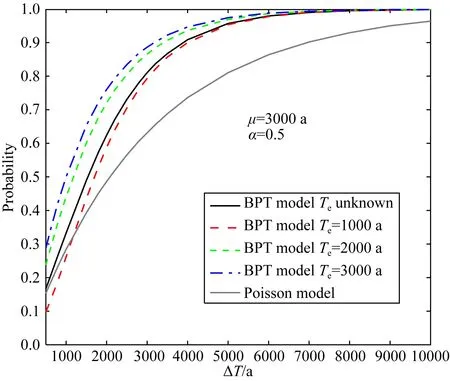
图7 BPT模型在离逝时间已知和未知情况下至少发生一次地震的条件概率的比较Fig.7 Comparison of BPT conditional probability of one or more events for the case in which the date of the last event is known and unknown

上述分析了在离逝时间未知情况下地震发生条件概率的计算，考虑了离逝时间所有的可能性.然而，在一些情况下，地震学家虽然未知断层上最近一次地震发生的具体时间，但却可以确定过去某一时刻到现在无地震发生，称之为历史开放间隔(historic open interval).这就缩小了离逝时间的范围.离逝时间的概率分布可由(10)式表示：

(10)

式中TH为历史开放时间间隔.那么未来一段时间至少有一次地震发生的条件概率可写为：

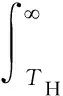
(11)

图8为已知历史开放时间间隔，采用BPT模型计算的条件概率相对于离逝时间完全未知的计算值的比值，称为概率增益.可以看出ΔT越小，概率增益越大，这是由于相对于离逝时间完全未知的情况，已知历史开放时间间隔时，断层更接近于失效状态，计算的条件概率相对于离逝时间未知情况下更大.

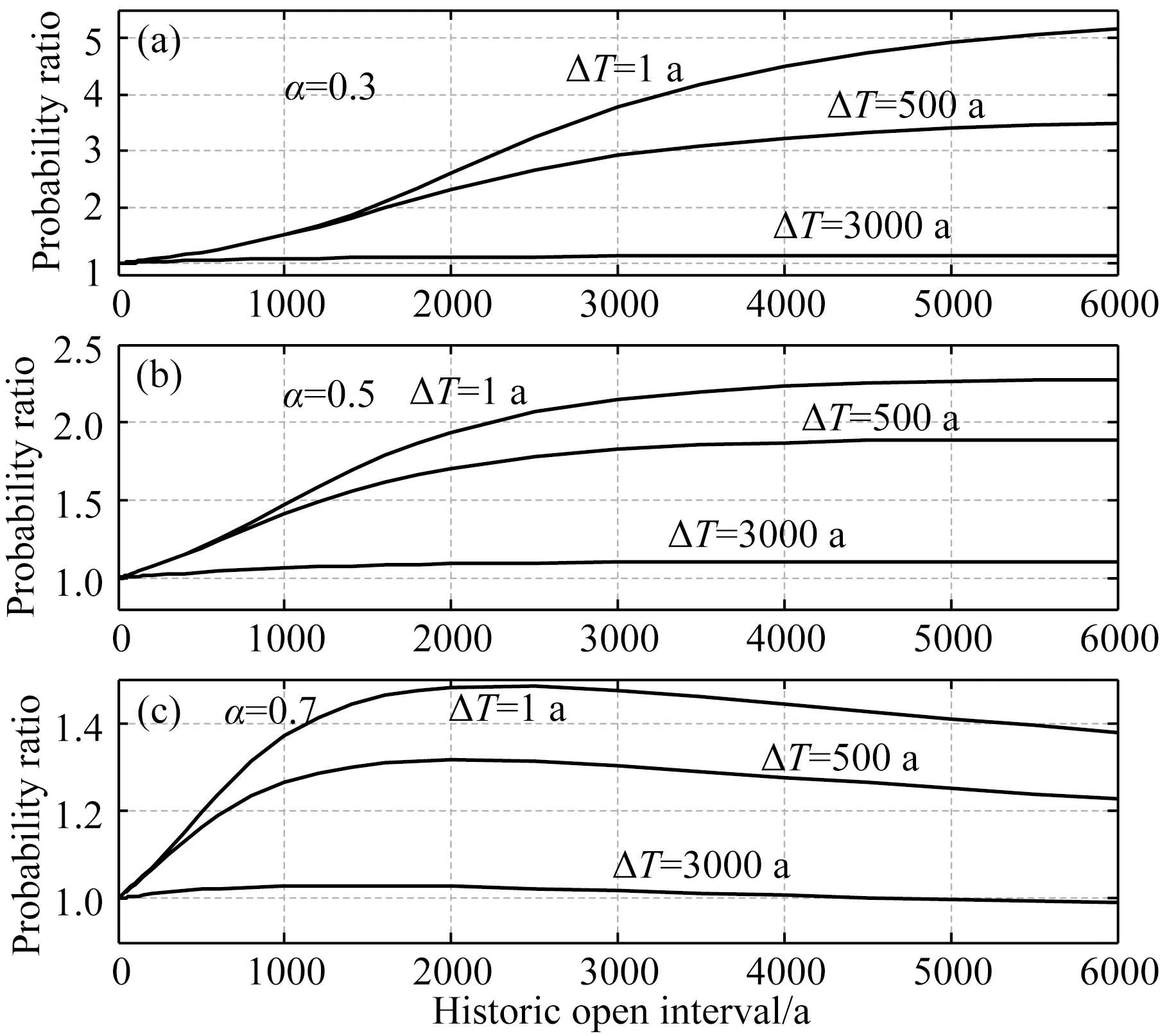
图8 考虑历史开放时间和离逝时间完全未知情况下BPT模型计算未来一段时间地震发生的条件概率的比值随历史开放时间的变化曲线图中不同曲线代表其所标注预测时间的结果，(a),(b)和(c)分别对应变异系数为0.3,0.5和0.7.Fig.8 BPT-model conditional probability of one or more events for the case in which the historic open interval is accounted for, divided by the probabilities for when the elapsed time is unknown, plotted against the open intervalThe alternative curves represent results for different forecast durations (ΔT) as labeled. (a), (b) and (c) are for aperiodicity (α) values of 0.3, 0.5 and 0.7, respectively.

2.3 等效地震发生率的计算

为了进行地震危险性计算，还需要知道特征地震在未来ΔT内的年发生率r.根据上文中的公式(6)、(9)和(11)可计算出特征地震在ΔT时段内的发生概率P.r仍然可看作服从泊松分布(Petersen et al., 2007)，那么P=1-exp(-r·ΔT)，则等效发生率为：

r=-ln(1-P)/ΔT.

(12)

图9为根据BPT模型计算的未来一段时间内的等效发生率.其中μ=3000 a，α=0.5，离逝时间分别为1000 a、2000 a和3000 a.可以看出在离逝时间较短，ΔT较小时，BPT模型的地震发生率小于泊松模型，这是由于在离逝时间较短时，断层上构造应力累积较小，发生地震的概率也较小.根据BPT模型的物理意义，某一特定断层上，未来一段时间发生地震的概率与上一次发生地震的离逝时间相关，离逝时间越久，则表示构造应力累积越大，发生地震的概率就越大，因此计算的等效发生率也越大.

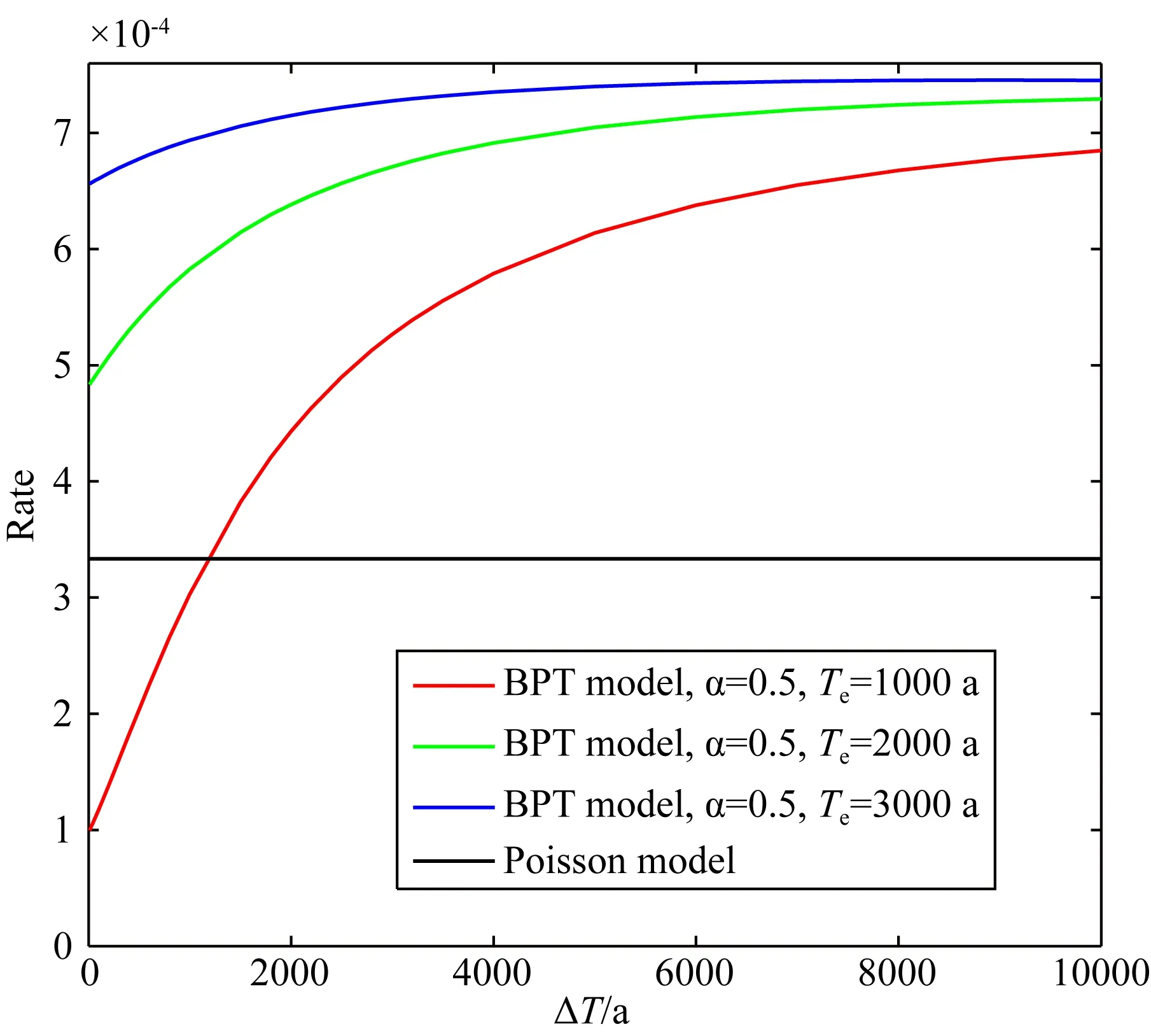
图9 根据BPT模型和指数模型计算的未来一段时间的等效发生率随着ΔT的变化曲线Fig.9 Seismic rate as a function of forecast durations (ΔT) for BPT model and Poisson model

3 基于布朗随机过程的地震加卸载过程

统计模型广泛应用于科学研究中，通过对事件时间序列的统计分析，可获知事件发生的时间特征.在地震学研究中，研究者们采用指数分布、对数正态分布、威布尔分布以及伽马分布等描述地震事件的时间序列过程.通过对这些模型进行经验拟合，研究者们可获知地震的时间分布特征.然而这些统计模型不能对地震发生的时间过程进行深刻的描述，存在物理意义不明确的问题(Matthews et al., 2002).Matthews等(2002)基于Reid(1910)的弹性回跳理论，并考虑构造应力、介质物性等物理量，提出了采用布朗运动来描述地震震源的加载过程.

设Y(t)为t时刻的断层震源加载状态，震源的加卸载过程可用(13)式表示：

Y(t)=x0+X(t)-X[R(t)],

(13)

其中x0为震源加载的初始状态，即Y(0)=x0；X(t)为从时间0到时间t的累积加载，X(t)=λt，λ为加载率；X[R(t)]为最近一次断层失效(地震发生)时的震源的累积加载，在断层失效后，震源立即回到初始加载状态.

将布朗随机扰动加入累积加载便可得到加载状态的随机过程：

X(t)=λt+σW(t),t≥0,

(14)

其中W为标准布朗运动，σ为随机扰动的幅度参数.标准布朗运动可通过对平稳增量进行积分得到，该平稳增量的分布为均值为零方差为常数的正态分布.

断层失效状态可写为：

xf=x0+δ,δ>0,

(15)

其中δ为可接受的最高累积加载.实际情况下失效状态下的加载是已知的.

根据上述描述，布朗更新过程可用平均加载率λ、随机扰动率σ、加载初始状态x0以及失效状态xf等四个参数来确定.布朗运动和布朗加卸载过程可分别用BM(x0,λ,σ)和BRO(x0,λ,σ,xf)来表示.图10显示了三种布朗加卸载过程：BRO(0,1,σ,1)，σ取值为0.25、0.5和1.0.可以看出在σ较小时，地震复发呈现明显的周期性.当σ较大时，地震发生的随机性显著增强.

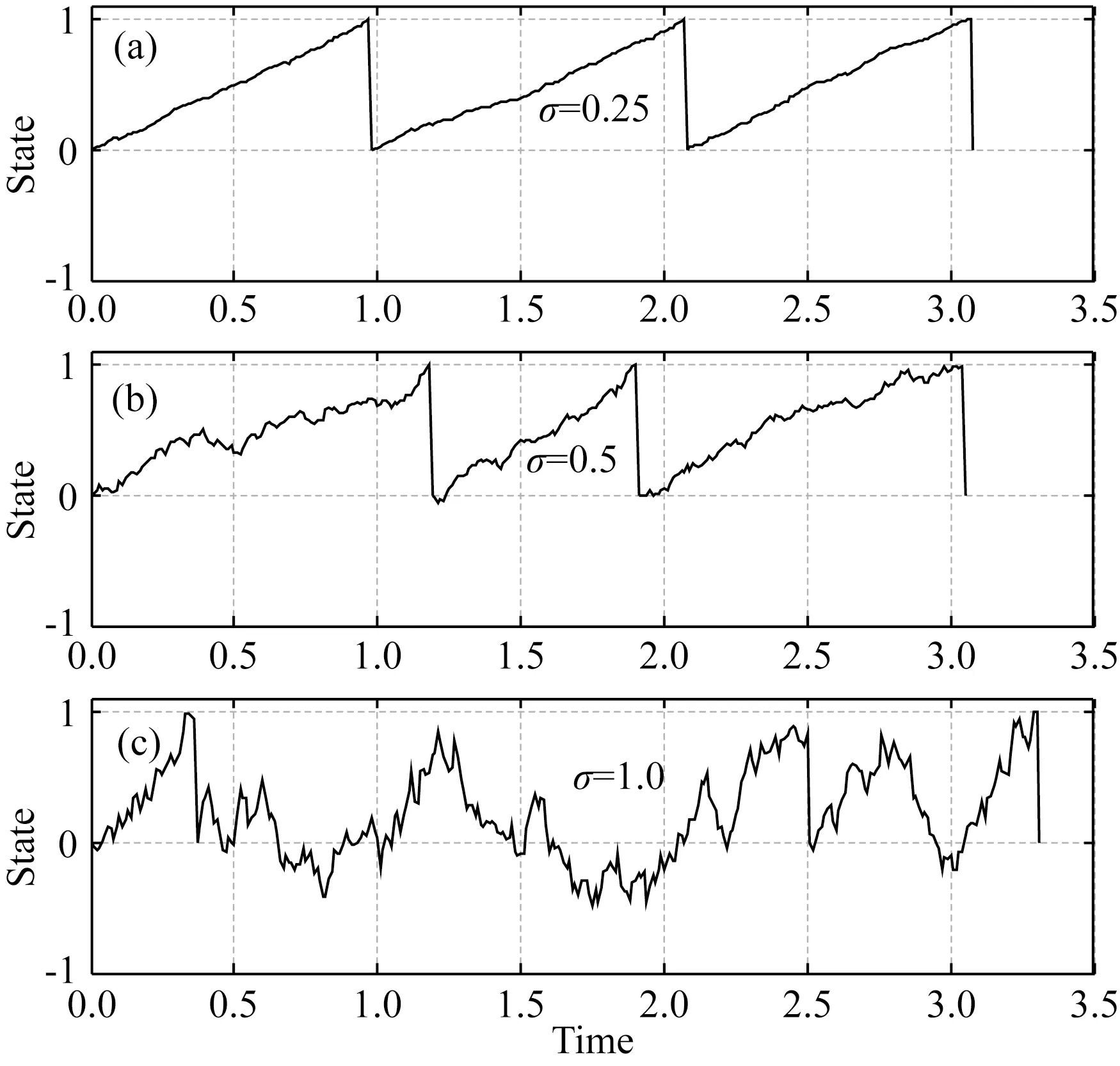
图10 λ=xf= 1时布朗加卸载过程路径状态曲线(a) σ=0.25, (b) σ=0.5, (c) σ=1.0.Fig.10 Load-state paths for a Brownian relaxation oscillator with λ=xf=1

地震的发生率(复发间隔的倒数)即是加载过程的加载率，复发间隔的不确定性是加载过程的随机扰动.离逝时间是加载时间.由此可预测未来一段时间断层应力的加载状态.上述中失效状态的时刻即是地震发生的时间，记录这些时间便得到符合时间相依分布的地震时间序列.由此可见，根据第2节计算的地震发生率(复发间隔)、复发间隔的不确定性以及地震离逝时间等参数，可采用基于布朗随机过程的地震加卸载过程来模拟地震的时间序列，这是基于时间相依地震事件模拟的最重要环节.

4 基于BPT模型的特征地震时间序列模拟实例

上文中系统介绍了时间相依的地震活动性模型、时间相依地震发生概率的计算方法以及基于布朗随机过程的地震加载过程理论，基于这些理论、模型和方法，我们模拟了符合时间相依准周期分布特征的地震序列.假设某一断层上地震复发间隔的均值为μ=3000 a，标准差α=0.25，以此参数模拟了时间相依的地震序列，并与具有相同μ值的泊松分布的地震序列进行了比较(图11).可以发现基于BPT模型模拟的地震序列呈现准周期分布的特征，而泊松地震序列则呈现出随机分布特征.

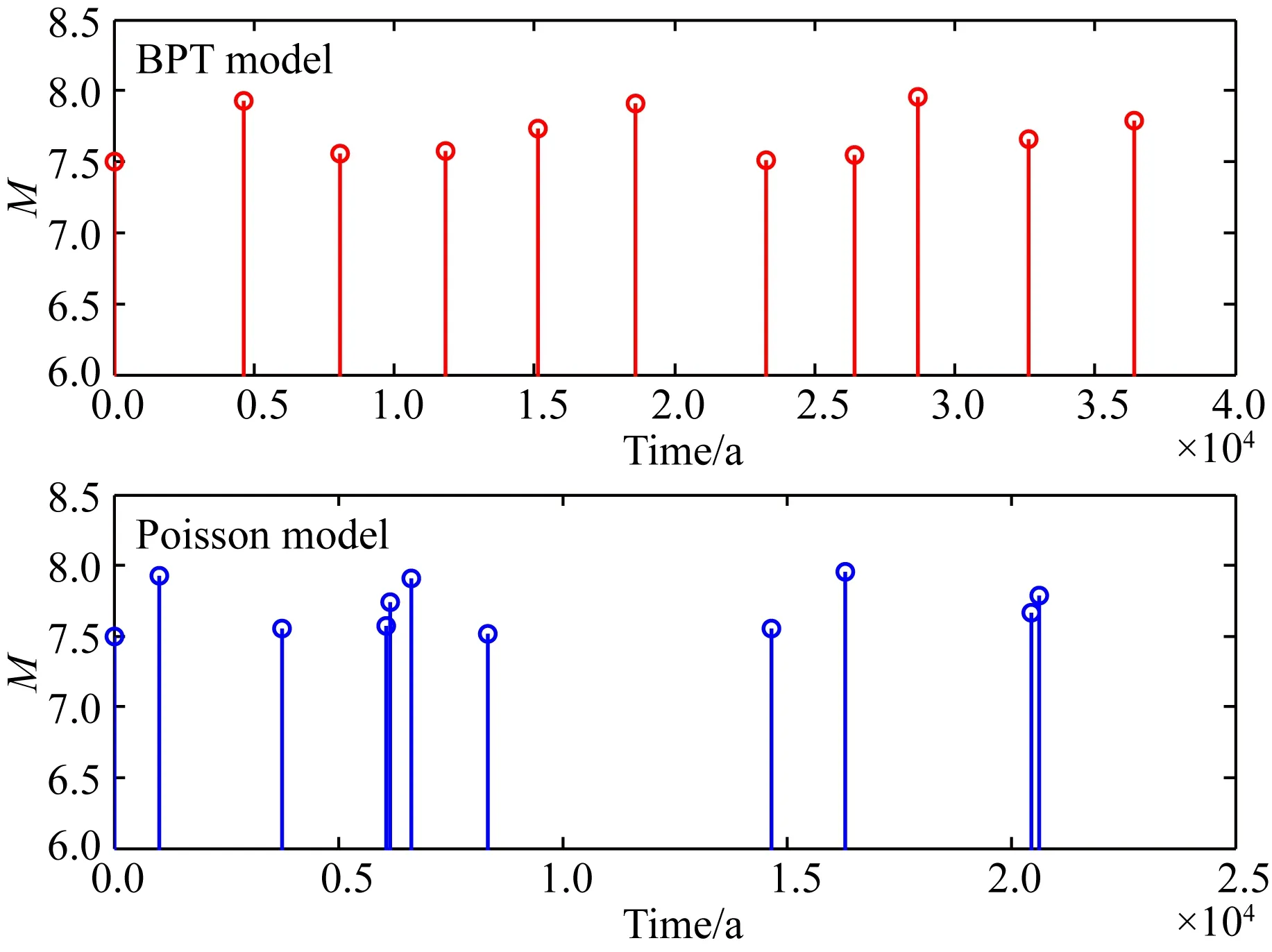
图11 基于BPT模型和泊松模型的模拟随机地震序列Fig.11 Simulation of random earthquake sequence based on BPT and Poisson models

基于BPT模型模拟的地震时间分布受标准差的影响，为了了解标准差对模拟地震序列时间分布特征的影响，我们模拟了不同标准差下(α=0.1，α=0.3，α=0.5，α=0.7)的BPT随机地震序列(图12)，可以看出，在标准差较小时，地震序列呈准周期分布，当标准差较大时，地震序列呈现随机性，这与上述BPT模型概率密度函数的分析是一致的.

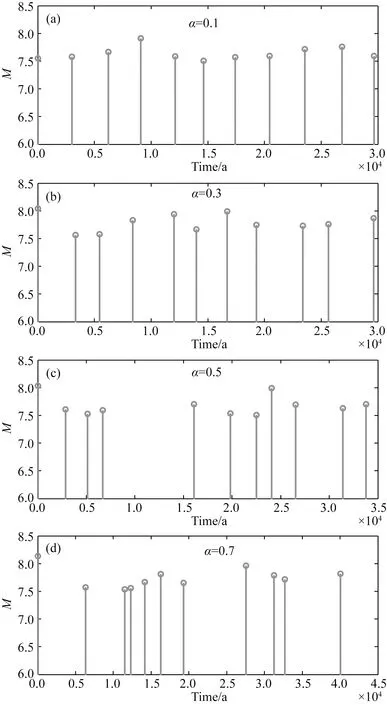
图12 在平均复发间隔为3000 a，变异系数分别为0.1、0.3、0.5和0.7时，基于BPT模型的随机模拟地震时间序列Fig.12 Simulated earthquake time series based on BPT model with a mean recurrence interval (μ) of 3000 a and aperiodicity (α) values of 0.1, 0.3, 0.5 and 0.7

上文完成了地震时间序列的实例模拟，模拟的地震时间序列能够体现时间相依特征，与理论模型是吻合的.一套地震序列，除了发震时间外，还有地震震级、发震位置等参数.对于震级，主要根据震级-频度关系(G-R关系)来模拟，也可根据历史地震目录中地震的震级随机抽取.关于地震位置，可依据地震的空间分布概率来确定，对于单条断层的特征地震，可根据断层几何形状、产状以及断层面上的物理参数来确定.具体方法可参考Xu等(2021).通过上述方法，可模拟一系列地震的时间、地震位置以及震级等参数，生成地震事件集，可用于地震预测、地震危险性分析以及地震灾害评估等领域.

5 结论与讨论

为了模拟具有时间相依特性的地震时间序列，本文系统研究了描述时间相依地震活动特征的理论、模型与方法.根据时间相依地震活动性模型及其参数特征，给出了已知和未知大地震离逝时间的情况下地震发生概率的计算流程以及等效发生率的计算方法.基于BPT加卸载过程，建立了大地震准周期复发模拟方法.以特征地震模型为例，进行了特征地震时间序列的模拟.与泊松时间序列相比，基于BPT模型的时间序列具有准周期性.此外，模拟特征地震时间序列受地震复发间隔标准差的影响，标准差越小，序列越趋于周期性，反之，时间序列则呈现随机性.

本文中，基于时间相依地震活动性模型模拟的地震事件与基于泊松模型的相比，主要有两个方面的差异，一是地震发生率的区别，对于泊松模型，地震年发生率是不随时间变化的，而时间相依地震活动性模型则相反，并且在地震离逝时间较长的情况下，基于时间相依的地震活动性模型计算的地震发生率要显著高于泊松模型，这对地震危险性分析具有重要影响.二者的第二个差异是在时间轴上的表现不同，本研究中模拟的时间相依的特征地震时间序列呈现周期性，而泊松模型时间序列是完全随机的.

本文模拟地震时间序列基于的是BPT模型，该模型的理论基础是弹性回跳学说，弹性回跳理论认为，在断层上发生一次特征地震后，构造应力急剧释放，后续短期内发生大地震的概率急剧减小，随着时间推移，构造应力重新累积，发震概率也随之增大.该理论目前被广泛用于地震预测和地震危险性分析.但是，实际情况下，由于一条断层上特征地震记录非常少，很难验证该理论的正确性.以后随着地震记录的增多，在一条断层上有多个特征地震发生，可对该理论进行验证.

本文介绍的方法对于提高地震概率预测水平具有重要意义.在任一断层上，通过本文介绍方法，可模拟一系列具有时间相依特征的地震事件集，并用于地震预测、地震危险性分析以及地震灾害评估等领域.本文研究成果已应用于中国地震巨灾保险模型的构建.