基于EWT-MQE的变压器局部放电特征提取
尚海昆,李宇才,林 伟
基于EWT-MQE的变压器局部放电特征提取
尚海昆,李宇才,林 伟
(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012)
为了有效提取局部放电信号故障特征,进而对电力变压器故障进行诊断,提出一种基于经验小波变换(Empirical Wavelet Transform, EWT)和多尺度量子熵(Multiscale Quantum Entropy, MQE)的变压器局部放电特征提取方法。首先,该方法利用EWT对局部放电信号进行分解,得到多个不同的固有模态分量(Intrinsic Mode Function, IMF)和残余分量。其次,计算信号分解出的每个IMF的多尺度量子熵序列。然后,对多尺度量子熵序列利用局部切空间排列算法(Local Tangent Space Arrangement, LTSA)进行降维处理。最后,采用层次聚类算法(Hierarchical Agglomerative Clustering, HAC)进行聚类分析,得到不同放电类型的识别结果。通过与不同诊断方法对比,仿真结果及实验数据验证了所提方法的有效性和优越性。
经验小波变换;多尺度量子熵;局部放电;变压器;层次聚类
0 引言
电力变压器作为电力系统的重要组成部分,其运行状态对整个电网的稳定运行具有重要意义[1-5]。由于变压器在现场难免会受到热应力、过载、绝缘材料老化、外部环境变化的影响,在持续的高压下工作进而导致绝缘故障,降低电网运行稳定性[6-7]。其中局部放电是造成绝缘劣化的重要表现形式,因此局部放电故障诊断对于保障设备绝缘安全具有重要现实意义[8-11]。
局部放电(Partial Discharge, PD)是一种微弱的放电现象,现场的局部放电有气隙放电、沿面放电、电晕放电等多种放电类型,其化学特性、热特性、微观放电过程难以通过肉眼直接观察。不同放电故障对设备产生的影响不同,因此可以通过对局部放电类型进行辨识,为变压器的检修工作提供有价值的技术支持[12]。
目前已有众多学者使用不同信号分析方法研究局部放电故障诊断,并取得了显著应用效果[13-15]。其中小波分析法由于预定义的窗口长度是固定的,在处理非平稳信号时,会发生过包罗和欠包罗以及模态混叠现象[16]。此外窗口傅里叶变换[17]、Wigner分布时频分析方法[18],在局部放电分析中也取得一定的应用效果,但这些方法容易受到噪声干扰的影响,具有一定的局限性。经验模态分解(Empirical Mode Decomposition, EMD)具有自适应分解的优势,但其自身存在模态混叠及端点效应,在实际应用中存在一定问题[19];集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)虽然克服了EMD的模态混叠问题,但存在残余噪声,会产生大量的伪信号,误差大,复杂性也高[20]。
而经验小波变换(Empirical Wavelet Transform, EWT)既具有EMD的自适应性又具有可靠的理论基础,其极大地减弱了EMD方法中存在的模态混叠现象,克服了端点效应问题[21]。文献[22]应用EWT进行地震信号时频域分析,结果比传统小波(CWT)有更好的分辨率,提供了更精确的地质和底层信息。文献[23]应用EWT进行心音异常检测,实验结果中的Oa指标高达93.3%,优于传统的希尔伯特振动分解(Hilbert Vibration Decomposition, HVD)算法。文献[24]提出一种结合EWT和成分分析的无线电指纹识别方法,结果表明,在信噪比比较低的情况下也能识别准确率良好,对噪声不敏感。因此本文尝试引入EWT算法对局部放电信号进行处理。
熵从信号序列的角度度量信号的复杂度,用来描述信息的不确定性[25]。量子熵通过对比相邻数值来衡量时间序列的复杂度,具有计算流程简单和鲁棒性较好等优点,被广泛地应用于信号特征提取领域。多尺度量子熵是衡量系统混乱程度的指标[26-28],反映各个频带能量分布的均匀度,来估计信号出现新模式的概率,抗噪声干扰能力较强,所需信号的数据量较少,很大程度上解决了依赖大量无噪声干扰数据的问题。
本文尝试使用EWT与多尺度量子熵相结合的方法提取局部放电特征,提取特征之后用局部切空间排列算法(Local Tangent Space Arrangement, LTSA)进行降维,利用层次聚类算法(Hierarchical Agglomerative Clustering, HAC)进行聚类,识别率达到96.7%,仿真和实验分析结果表明该方法能够有效实现局部放电故障识别。
1 算法及原理介绍
1.1 经验小波变换原理介绍
经验小波变换先是对信号进行自适应傅里叶分解,可以根据信号得到不同的频域特征,然后用局部极大值优化频谱分割边界,之后在每个尺度上构造经验尺度函数和经验小波函数,细节函数为经验小波与原函数的内积,分解出IMF[29]。


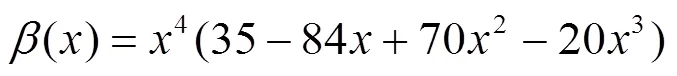
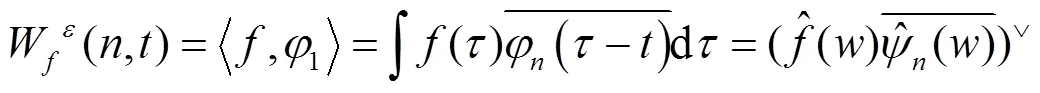
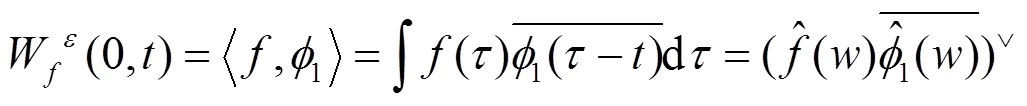


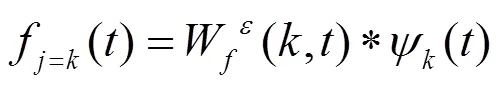
1.2 多尺度量子信息熵原理(MQE)
信息熵是描述系统不确定性的物理量,所以它也可以反映局部放电的内部变化情况[30]。
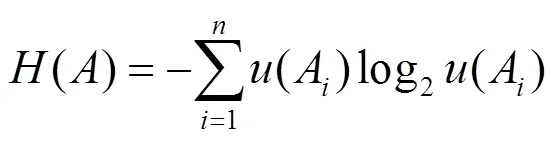

1) 重构分量的量子化
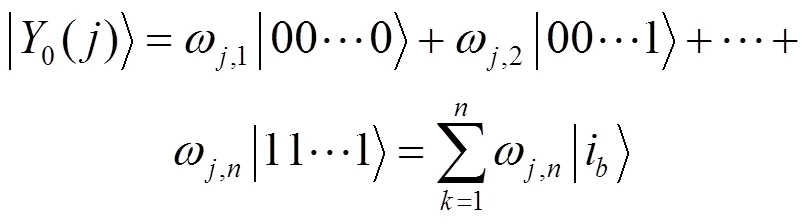
2) 计算各态矢概率
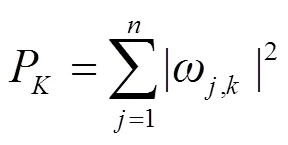
将各态矢出现的概率作为事件出现的概率,计算信息熵。
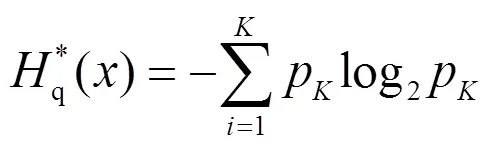
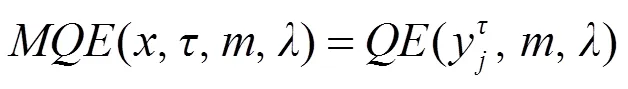
计算每个尺度因子下的粗粒向量的量子熵值,称为多尺度量子熵[23]。
2 仿真分析
2.1 局部放电仿真信号
局部放电信号是一种瞬态信号,当变压器中的绝缘材料局部区域的电场强度超过可以承受的最大值时,便形成了局部放电现象。结合放电原理和前人实验,纯净局部放电信号可以用双指数衰减和双指数振荡衰减两个数学模型来等效。该模型是在综合局部放电微观过程中电荷的扩散、积累和复合等因素之后建立的仿真模型,能够对局部放电进行有效的模拟,如式(15)、式(16)所示。
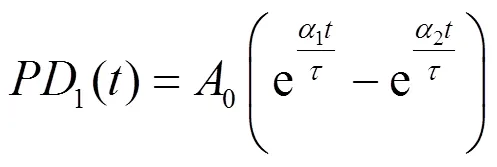

参数配置如表1所示,得到局部放电脉冲波形如图1所示。

表1 仿真信号参数
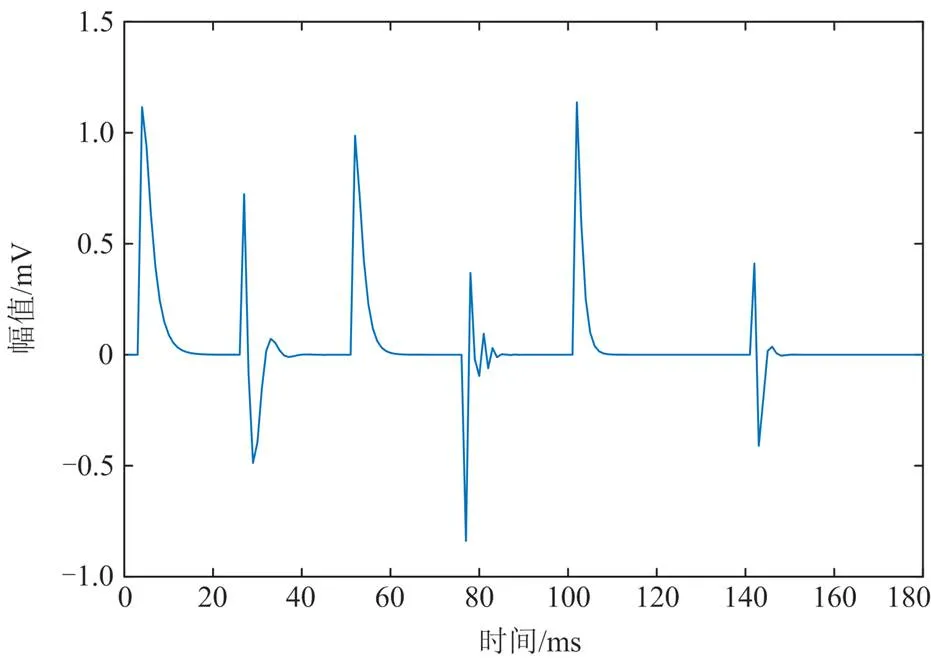
图1 仿真信号波形
由图1可见,模拟局部放电信号由6个脉冲构成,每个脉冲具有不同的波形特征。
2.2 EWT仿真分析
EWT算法能够分解非线性非平稳信号,且具有重构误差小的特点,本文应用EWT对局部放电信号进行分析。为了验证EWT的优越性,引入EMD和EEMD对2.1节仿真信号进行分析,EMD、EEMD、EWT参数如表2所示,信号分解结果如图2所示。
由图2(a)可得,EMD方法分解结果虽然能将信号的高频分量和低频分量分开,但是EMD算法本身缺乏完备的理论基础,存在端点效应问题和模态混叠现象。由图2(b)可知,EEMD在一定程度上减轻了模态混叠现象,但是还是不能完全消除虚假分量对分析产生的影响。由图2(c)所示,EWT分解仿真信号得到5个模态分量IMF1、IMF2、IMF3、IMF4、IMF5。低频分量变化较平缓,高频分量波形变换较剧烈包含了信号的峰值信息和突变信息,且有效消除了模态混叠现象,解决了虚假分量干扰的问题。综上分析,通过EWT分解能够获取丰富的局部放电信息,可以更好地表征局部放电信号。

表2 参数配置

3 基于EWT-MQE变压器局部放电故障诊断
本文首先进行局部放电实验信号采集,然后利用EWT算法对采集的不同类型的局部放电信号进行分解,得到多个IMF,然后计算模态分量的多尺度量子熵作为特征参数。由于得到的多尺度量子熵数据维数较高,不便于后续处理,因此本文继续运用LTSA算法进行降维,获取低维特征平面,最后进行HAC聚类识别,得到局部放电故障诊断的识别结果。图3为局部放电故障诊断的整体流程图。

图3 局部放电诊断方案流程图
3.1 局部放电信号获取
文中采用保定天威新域科技发展有限公司生产的TWPD-2E多通道数字式局部放电综合分析仪对局部放电信号进行采集。图4为3种放电模型的物理结构。

图4 局部放电模型的物理结构
试验系统采集放电信号使用的是电感耦合式传感器作为输入单元,这样可以有效采集到交流信号,阻断直流信号,从而抑制共模信号的干扰。本实验方案的采样频率为50 MHz,采集得到的不同类型的放电信号如图5所示。
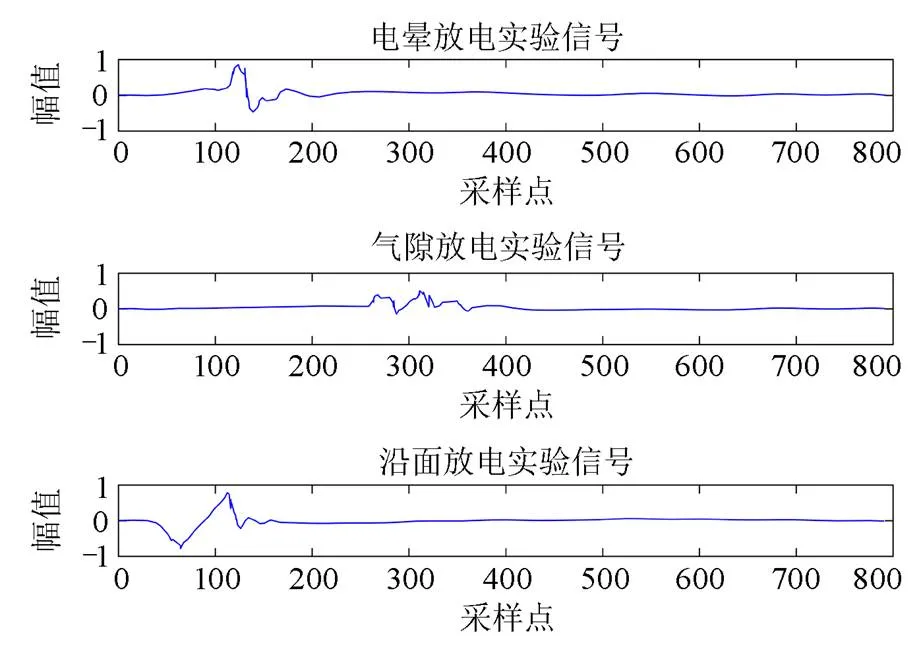
图5 局部放电试验波形
图5表明不同类型的放电信号具有不同的特征。为了量化局部放电特征,提取出能够表征放电信号的有效信息,本文尝试EWT与多尺度量子熵结合用于局部放电特征提取。
3.2 EWT分解
为了获取放电信号的细节信息,对实验信号进行EWT分解,如图6所示。
由图6可见,不同类型的局部放电信号经过经验小波变换,得到有一定规律的经验模态分量,每个分量都有不同的周期性和幅值,分别对应着不同尺度上的特征。不同局部放电信号的细节信息具有明显差异,每种类型放电信号的分解结果中,不同模态周期性特点差距较大,EWT有效解决了模态混叠问题。
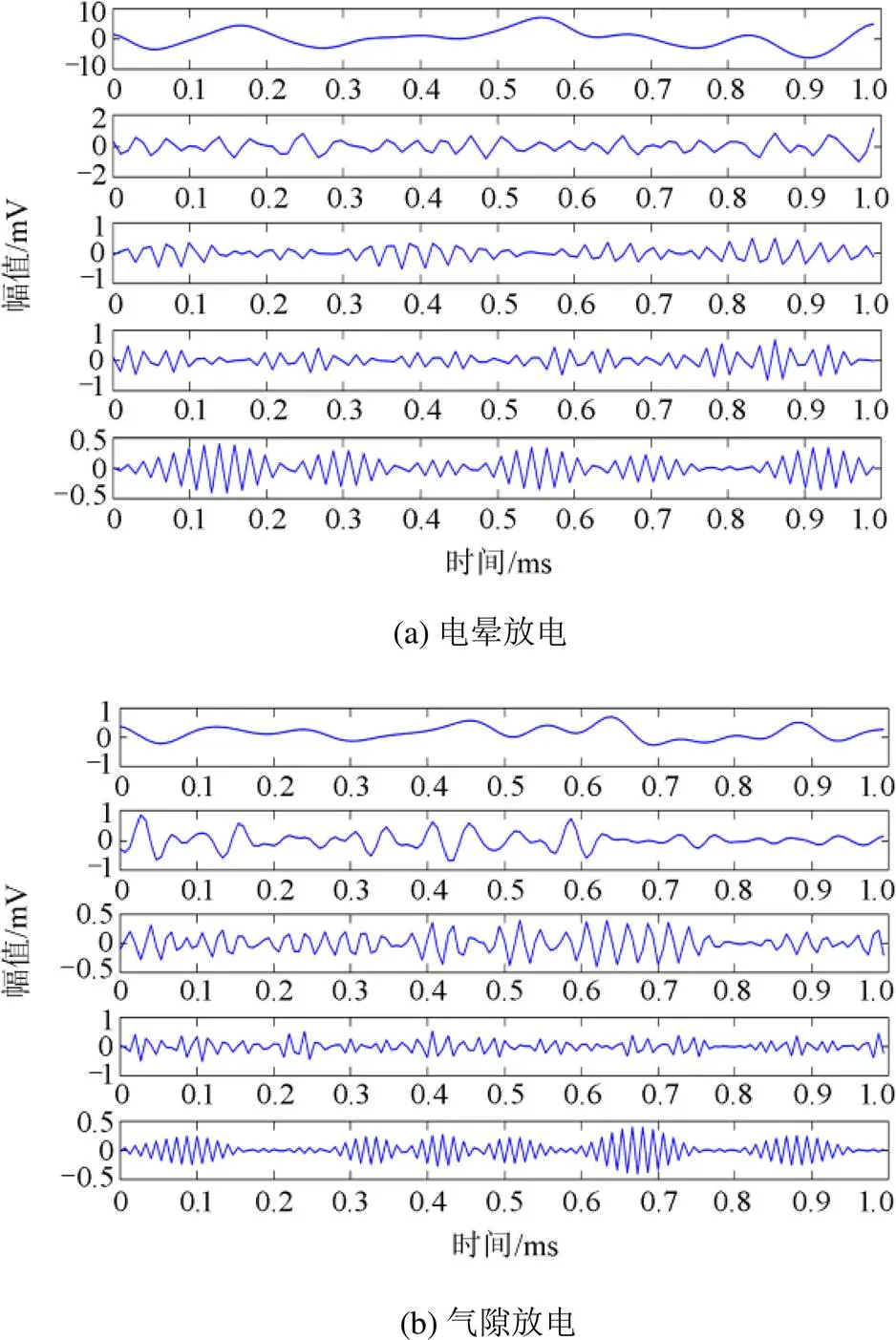
3.3 多尺度量子熵计算
为了对不同放电信号特征进行量化分析,本文引入多尺度量子熵对局部放电信号的IMF分量进行分析。
3种放电信号在进行EWT算法处理之后,对每一个模态分量进行多尺度量子熵计算,得到不同尺度的熵值如图7所示。
由图7可得,不同放电类型具有的多尺度量子熵值明显不同。多尺度量子熵是一种无量纲参数,由于多尺度量子熵值的大小可以反映信号分解后模态分量的复杂程度,熵值越大,该尺度上的混乱程度越高。通过熵值分析可见,复杂的多尺度量子熵高维信息空间能充分包含局部放电丰富的特征信息。当放电特征维度较大时,会导致后续的识别算法难度增加。为了提高识别效率,本文对高维特征进行降维处理。
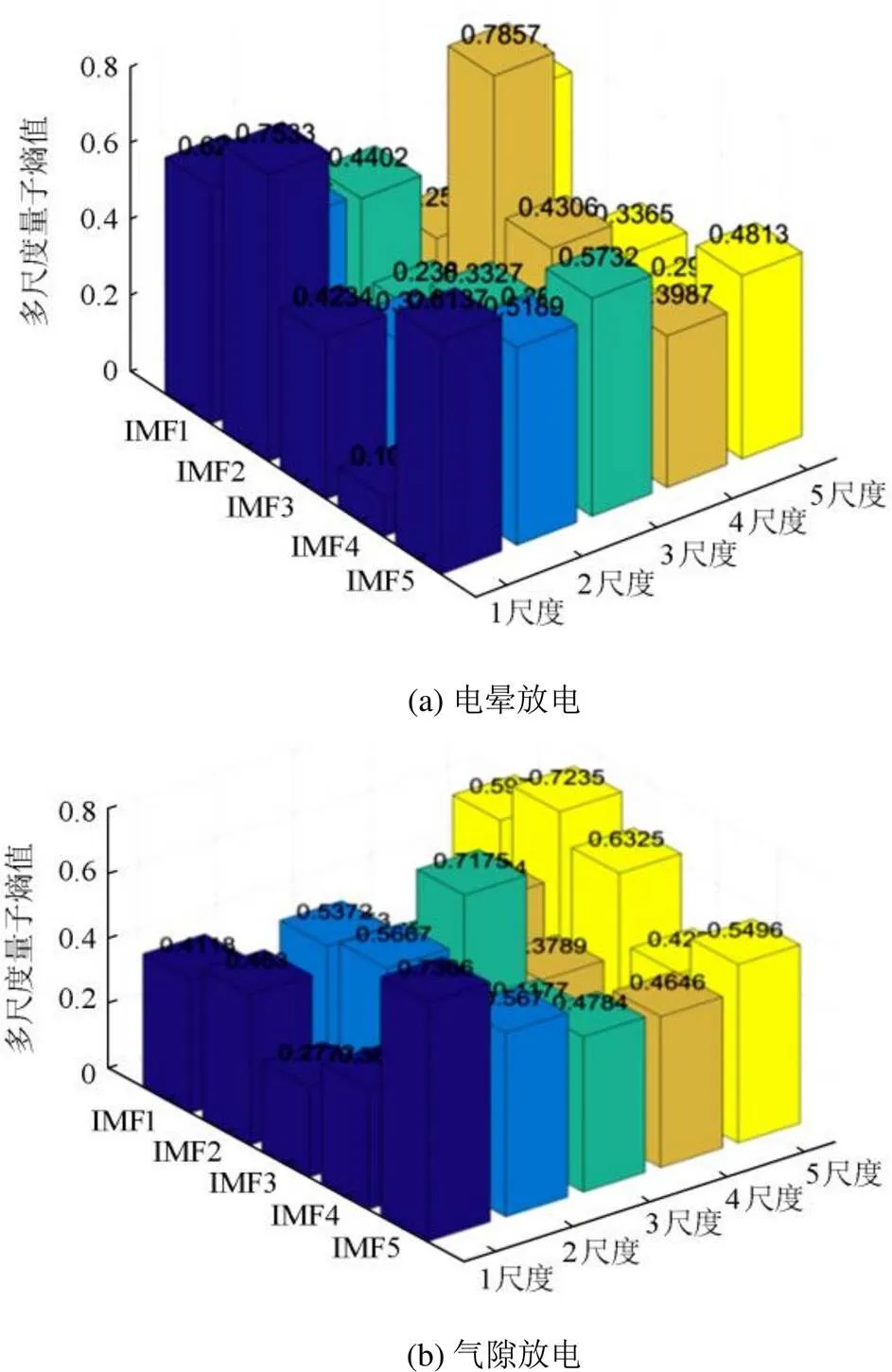
3.4 特征降维
在局部放电模式识别过程中,高维特征参数包含的无关和冗余特征可能会降低识别的精确性,所以对上节得到的局部放电高维特征进行降维处理。LTSA在全局非线性结构中,依靠切空间逼近所有数据点的思路来实现低维流形的局部细节表述,LTSA通过求解输入数据点局部切空间的投影得到局部低维坐标,然后交错的局部低维坐标通过局部仿射变换输出全局低维坐标。这种降维方法可以实现保持原始数据整体分布信息的目的,使降维结果保留更多信息[31]。
本文引入LTSA进行特征降维[31]。LTSA算法首先应用切空间排列获得高维样本的切空间局部坐标,然后构建变换矩阵,线性拟合得到低维全局嵌入坐标,最后通过最小化全局误差,重构嵌入坐标。算法原理如图8所示。
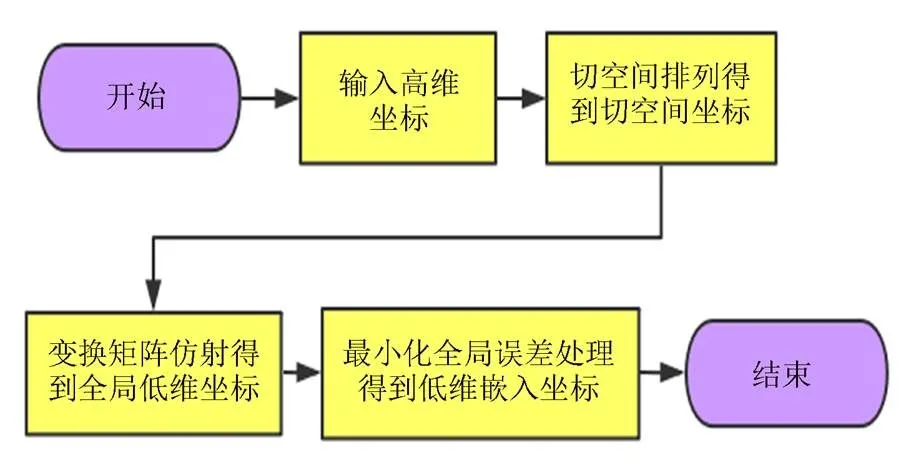
图8 LTSA降维过程
LTSA算法需要调节的参数包括邻域参数、维数参数和收敛阈值,分别配置为3、2、2×10-3。以4.3节电晕放电信号为例,降维得到的嵌入坐标为(3.0770, 3.7587)。该方法具有操作简单和运算时间短的优点,每组数据降维处理仅需耗时1.1 s,并且LTSA算法降维后的各状态点保留特征信息效果较好,能够减小后续聚类算法的误差,提高识别精度。同理可将所有局部放电特征降维处理。
为了验证多尺度量子熵的优越性,本文引入多尺度样本熵(MSE)和多尺度能量熵(MEE)进行对比分析,参数如表3所示。运用前面获取的EWT分析结果进行熵值计算,之后利用LTSA算法降维处理,结果如图9所示。
图9为3种多尺度熵高维信息降维后的结果。由图9(a)可见,对于局部放电信号MEE特征提取方法,3种放电类型的样本在低维空间有较多样本分布重叠,并且同一类样本的分布半径比较大,归其原因为MEE在高维空间特征提取时,辨识相似特征放电的能力有缺陷。图9(b)为MSE特征提取方法,该方法得到的局部放电特征虽然重叠区域明显减小,但每种放电特征的分布半径依然较大,并且3种类型的放电样本边界不清晰。图9(c)为MQE特征提取后的结果,可见每一类样本分布比较集中,特征内聚性很好,不存在交叉重叠现象。

表3 MQE、MEE和MSE参数配置

图9 多尺度熵结果
3.5 识别结果
为了识别不同局部放电故障类型,本文采用HAC聚类方法[32]对低维特征信息进行故障识别。分别取100个电晕放电样本、100个气隙放电样本、100个沿面放电样本进行分析。
为了验证本文方法的优越性,引入不同诊断方法进行放电类型识别。本文将K-means聚类、Descan聚类和HAC聚类3种故障诊断方法进行对比,均在Matlab2015环境下进行。为了量化诊断效果,引入戴维森堡丁指数(DBI)和轮廓系数(SIL)作为聚类指标评判,并且结合识别率和识别时间进行对比。
DBI指标表示簇之间的平均相似度,其中相似度通过簇内距离与簇间距离的比值来表示。DBI的最小值为0,该值越小表示聚类效果越好[33-34]。SIL表示单个数据聚类效果,它的取值范围为[-1,1],越接近1则表示聚类效果越好[35]。
分别对K-means、Descan、HAC聚类结果求取DBI和SIL,结果如图10所示。

图10 3种聚类方案的DBI和平均SIL对比图
由图10可以看出,在确定相同聚类数的前提下,HAC聚类方法DBI指标最小,且SIL指标最大,聚类质量最佳,相比于传统的K-means算法和Descan算法,HAC具有更好的聚类效果。
为了验证本文提出的HAC聚类方法在局部放电故障诊断中的有效性,实验样本采用本文所提的特征提取方法之后分别进行K-means、Descan和HAC聚类,识别结果如图11所示,识别率如图12所示。


图12 不同方法的识别率
图11为不同聚类方法的识别结果。由图11(a)可见,K-means聚类结果中55个样本识别错误,其中12个电晕放电样本误判为气隙放电,8个气隙样本误判为电晕放电,可见对于电晕放电和气隙放电,该方法识别效果较差。由图11(b)可得,Descan中有29个样本识别错误,其中电晕放电和气隙放电仍有27个样本被误判,说明Descan对于相似类型的放电样本仍然不能有效识别。由图11(c)可见,HAC算法在识别过程中能够较为准确地识别出不同局部放电故障,效果明显优于前面两种聚类方法。
由图12可得,HAC聚类结果识别率高达96.7%,明显高于K-means的81.7%和Descan的90.3%,表明HAC聚类能够解决传统聚类算法中对聚类中心的依赖问题,有效识别出局部放电故障类型,与K-means和Descan相比具有更高的识别率,可以很好地应用在局部放电故障诊断领域。
4 结论
局部放电信号诊断对于保证变压器绝缘安全具有重要的现实意义。本文提出基于EWT和MQE的局部放电特征提取方法,主要结论如下述。
1) EWT算法克服了模态混叠现象,解决了端点效应问题,解决了EMD的过包罗、欠包罗和对低频信息特征提取较差的问题,也解决了EEMD计算量大,复杂度高的弊端,克服了基线漂移和基线失真问题,保持较好的放电信号形态特征。
2) MQE能够有效反映时间序列复杂程度,从放电信号的模态分量的多尺度量子熵计算结果可以看出,多尺度量子熵能够挖掘深层次时序特征信息,较好地表征局部放电信号特征,与MSE和MEE相比更具优势。
3) LTSA方法能够实现局部放电特征参数降维,保留高维特征的有效信息,HAC自适应聚类解决了传统结果中对聚类中心的依赖,在局部放电故障诊断中识别率达到96.7%,相比传统的K-means和Descan聚类,具有更优的诊断性能。
综上分析,本文提出的局部放电故障诊断方法,能够融合EWT和MQE各自的优势,有效提取出丰富的局部放电信号特征,利用LTSA和HAC方法能够对局部放电故障进行有效识别,为局部放电诊断提供了一种新思路。
[1] 谭贵生, 曹生现, 赵波, 等. 基于关联规则与变权重系数的变压器状态综合评估方法[J]. 电力系统保护与控制, 2020, 48(1): 88-95.
TAN Guisheng, CAO Shengxian, ZHAO Bo, et al. An assessment of power transformers based on association rules and variable weight coefficients[J]. Power System Protection and Control, 2020, 48(1): 88-95.
[2] 彭丽维, 张彼德, 孔令瑜, 等. 监督自适应核熵成分分析特征提取的电力变压器故障诊断[J]. 高压电器, 2020, 56(6): 249-255, 261.
PENG Liwei, ZHANG Bide, KONG Lingyu, et al. Power transformer fault diagnose based on supervised adaptive kernel entropy component analysis feature extraction[J]. High Voltage Apparatus, 2020, 56(6): 249-255, 261.
[3] 苑津莎, 王玉鑫, 刘铟, 等. 基于知识推理的变压器局部放电故障检测技术[J]. 电测与仪表, 2020, 57(13): 1-5.
YUAN Jinsha, WANG Yuxin, LIU Yin, et al. Partial discharge fault detection technology for transformer based on knowledge reasoning[J]. Electrical Measurement & Instrumentation, 2020, 57(13): 1-5.
[4] 刘东超, 林语, 原辉, 等. 灰度纹理与油气特征融合的油纸绝缘老化状态评估[J]. 中国电力, 2020, 53(12): 159-166, 197.
LIU Dongchao, LIN Yu, YUAN Hui, et al. Aging state evaluation of oil-paper insulation based on fusion of gray texture and oil gas features[J]. Electric Power, 2020, 53(12): 159-166, 197.
[5] 田天, 周秀, 丁培, 等. 交直流电压下油纸绝缘典型缺陷的局部放电特征[J]. 电力科学与技术学报, 2021, 36(6): 40-46.
TIAN Tian, ZHOU Xiu, DING Pei, et al. Partial discharge characteristics of typical defects in oil paper insulation under AC and DC voltage[J]. Journal of Electric Power Science and Technology, 2021, 36(6): 40-46.
[6] MA D, JIN L, HE J, et al. Classification of partial discharge severities of ceramic insulators based on texture analysis of UV pulses[J]. High Voltage, 2021(5): 1-10.
[7] 韩宝国, 马驰, 李静鹏, 等. 基于DTCWT与LLE算法的变压器局部放电特高频信号特征参数提取方法[J]. 电力系统保护与控制, 2019, 47(20): 65-72.
HAN Baoguo, MA Chi, LI Jingpeng, et al. A feature parameters extraction method of PD UHF signal based on DTCWT and LLE algorithm[J]. Power System Protection and Control, 2019, 47(20): 65-72.
[8] 王建元, 梁惠娟, 康爱民. 国内电力变压器局部放电超声波定位研究进展[J]. 东北电力大学学报, 2019, 39(2): 10-14.
WANG Jianyuan, LIANG Huijuan, KANG Aimin. Researches of power transformer partial discharge location using ultrasonic method in China[J]. Journal of Northeast Electric Power University, 2019, 39(2): 10-14.
[9] 王泉, 粱永昌, 李秋惠, 等. 基于SA-APSO及降维投影-动态加权统计的局部放电定位方法[J]. 广东电力, 2020, 33(6): 66-72.
WANG Quan, LIANG Yongchang, LI Qiuhui, et al. A positioning approach based on SA-APSO and reduced dimension-dynamic weighting statistics for partial discharge source[J]. Guangdong Electric Power, 2020, 33(6): 66-72.
[10]彭炜文, 刘伟杰, 许家浩, 等. 一种基于相关系数的EEMD局部放电去噪方法[J]. 高压电器, 2021, 57(6): 203-209.
PENG Weiwen, LIU Weijie, XU Jiahao, et al. EEMD partial discharge de-noising method based on correlation coefficients[J]. High Voltage Apparatus, 2021, 57(6): 203-209.
[11]姚维强, 司文荣, 傅晨钊, 等. 基于三参数威布尔模型的局部放电谱图特征提取[J]. 高压电器, 2021, 57(8): 184-190.
YAO Weiqiang, SI Wenrong, FU Chenzhao, et al. Feature extraction of PD spectrum based on three-parameter Weibull model[J]. High Voltage Apparatus, 2021, 57(8): 184-190.
[12] 姚锐, 李俊, 惠萌, 等. 基于集成学习的自适应提升分类模型的局部放电识别研究[J/OL]. 电网技术: 1-11 [2022-01-12]. DOI: 10.13335/j.1000-3673.pst.2021.0780.
YAO Rui, LI Jun, HUI Meng, et al. Pattern recognition for partial discharge using adaptive boost classification model based on ensemble method[J/OL]. Power System Technology: 1-11[2022-01-12]. DOI: 10.13335/j.1000-3673. pst.2021.0780.
[13] JANANI H, JAYASINGHE P, JOZANI M J, et al. Statistical feature extraction and system identification algorithms for partial discharge signal classification using Laguerre polynomial expansion[J]. Transactions on Dielectrics and Electrical Insulation, 2020, 27(6): 1924-1932.
[14] WANG Y, CHANG D, QIN S, et al. Separating multi- source partial discharge signals using linear prediction analysis and isolation forest algorithm[J]. Transactions on Instrumentation and Measurement, 2020, 69(6): 2734-2742.
[15] WAN L, HAN G, SHU L, et al. PD source diagnosis and localization in industrial high-voltage insulation system via multimodal joint sparse representation[J]. Transactions on Industrial Electronics, 2016, 63(4): 2506-2516.
[16] LIU W, CAO S, CHEN Y. Seismic time–frequency analysis via empirical wavelet transform[J]. Geoscience and Remote Sensing Letters, 2016, 13(1): 28-32.
[17] PLATAS-GARZA M A, DE L. Dynamic harmonic analysis through Taylor–Fourier transform[J]. Transactions on Instrumentation and Measurement, 2011, 60(3): 804-813.
[18] CHO S, JANG G, KWON S. Time-frequency analysis of power-quality disturbances via the Gabor-Wigner Transform[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 494-499.
[19]李高望, 张智, 李达, 等. 基于Prony分析特征提取的同调机组分群方法[J]. 电力系统保护与控制, 2020, 48(22): 91-99.
LI Gao, ZHANG Zhi, LI Da, et al. Coherency clustering method based on Prony analysis feature extraction[J]. Power System Protection and Control, 2020, 48(22): 91-99.
[20] GAO S, WANG Q, ZHANG Y. Rolling bearing fault diagnosis based on CEEMDAN and refined composite multiscale fuzzy entropy[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-8.
[21]马星河, 张登奎, 朱昊哲, 等. 基于EWT的高压电缆局部放电信号降噪研究[J]. 电力系统保护与控制, 2020, 48(23): 108-114.
MA Xinghe, ZHANG Dengkui, ZHU Haozhe, et al. Study on noise reduction of HV cable partial discharge based on EWT[J]. Power System Protection and Control, 2020, 48(23): 108-114.
[22] LIU W, CAO S, CHEN Y. Seismic time–frequency analysis via empirical wavelet transform[J]. Geoscience and Remote Sensing Letters, 2016, 13(1): 28-32.
[23] LI H, REN Y, ZHANG G, et al. Detection and classification of abnormities of first heart sound using empirical wavelet transform[J]. IEEE Access, 2019, 7: 139643-139652.
[24]张敏, 罗正华, 黄建刚. 一种结合EWT和成分分析的无线电指纹提取方法[J]. 计算机测量与控制, 2019, 27(4): 128-133.
ZHANG Min, LUO Zhenghua, HUANG Jiangang. A radio fingerprint extraction method combining EWT and component analysis[J]. Computer Measurement & Control, 2019, 27(4): 128-133.
[25] 田业, 徐天奇, 李琰, 等. 基于重构误差及多尺度交叉样本熵的谐振接地系统故障选线[J]. 电力系统保护与控制, 2021, 49(13): 95-104.
TIAN Ye, XU Tianqi, LI Yan, et al. Fault line selection of resonant grounding system based on reconstruction error and multiscale cross sample entropy[J]. Power System Protection and Control, 2021, 49(13): 95-104.
[26]刘丽丽, 田晶, 刘广鑫, 等. 基于多尺度量子熵的中介轴承声发射信号故障特征提取技术研究[J]. 沈阳航空航天大学学报, 2020, 37(2): 1-9.
LIU Lili, TIAN Jing, LIU Guangxin, et al. Research on fault feature extraction technology of acoustic emission signal of inter-shaft bearing based on multi-scale quantum entropy[J]. Journal of Shenyang Aerospace University, 2020, 37(2): 1-9.
[27] 丁闯, 张兵志, 冯辅周, 等. 非线性量子信息熵及其在行星变速箱特征提取中应用[J]. 振动与冲击, 2018, 37(23): 120-125, 148.
DING Chuang, ZHANG Bingzhi, FENG Fuzhou, et al. Nonlinear quantum entropy and its application in feature extraction for planetary gearboxes[J]. Journal of Vibration and Shock, 2018, 37(23): 120-125, 148.
[28]宦飞, 王志中, 郑崇勋. 睡眠EEG的多尺度信息熵分析[J]. 北京生物医学工程, 2001, 20(1): 6-8.
HUAN Fei, WANG Zhizhong, ZHENG Chongxun. Analysis of sleep EEG by using multi-scale entropy[J]. Beijing Biomedical Engineering, 2001, 20(1): 6-8.
[29]毕潇文, 钟俊, 张大堃, 等. 基于改进奇异值与经验小波分解的局放去噪算法[J]. 电网技术, 2021, 45(12): 4957-4963.
BI Xiaowen, ZHONG Jun, ZHANG Dakun, et al. Partial discharge denoising algorithm based on improved singular value and empirical wavelet decomposition[J]. Power System Technology, 2021, 45(12): 4957-4963.
[30]邵宝珠, 李胜辉, 白雪, 等. 非负约束自动编码器在电缆早期故障识别中的应用[J]. 电力系统保护与控制, 2019, 47(2): 22-29.
SHAO Baozhu, LI Shenghui, BAI Xue, et al. Application of a non-negative constraint autoencoder in cable early fault identification[J]. Power System Protection and Control, 2019, 47(2): 22-29.
[31]刘璐, 邱明, 李军星, 等. 基于LTSA融合降维法的滚动轴承可靠性评估方法[J]. 航空动力学报, 2021, 36(2): 413-420.
LIU Lu, QIU Ming, LI Junxing, et al. Reliability evaluation method of rolling bearing based on LTSA fusion dimension reduction method[J]. Journal of Aerospace Power, 2021, 36(2): 413-420.
[32] KOTOUZA M T, PSOMOPOULOS F E, MITKAS P A. A dockerized framework for hierarchical frequency-based document clustering on cloud computing infrastructures[J]. Journal of Cloud Computing, 2020, 9(1).
[33] 孙哲. 基于自适应层次聚类的无绝缘轨道电路补偿电容故障诊断方法[J]. 铁道标准设计, 2020, 64(3): 154-159.
SUN Zhe. A fault diagnosis method for compensation capacitor of JTC based on self-adaptive hierarchical cluster[J]. Railway Standard Design, 2020, 64(3): 154-159.
[34]唐菓, 邢承滨, 朱磊, 等. 利用层次聚类对移动曲面拟合滤波算法快速分类的研究[J]. 测绘工程, 2021, 30(3): 32-40.
TANG Guo, XING Chengbin, ZHU Lei, et al. Fast classification of moving surface fitting filtering algorithm based on hierarchical clustering[J]. Engineering of Surveying and Mapping, 2021, 30(3): 32-40.
[35]黄冬梅, 葛书阳, 胡安铎, 等. 采用中心优化和双尺度相似性度量的改进K-means负荷聚类方法[J]. 电力系统及其自动化学报, 2021, 33(12): 93-100.
HUANG Dongmei, GE Shuyang, HU Anduo, et al. Improved K-means load clustering method based on center optimization and double-scale similarity measurements[J]. Proceedings of the CSU-EPSA, 2021, 33(12): 93-100.
Partial discharge feature extraction of a transformer based on EWT-MQE
SHANG Haikun, LI Yucai, LIN Wei
(Key Laboratory of Modern Power System Simulation & Control and Renewable Energy Technology,Ministry of Education, Northeast Electric Power University, Jilin 132012, China)
To effectively extract the partial discharge fault feature and diagnose the fault of a power transformer, this paper presents a method based on empirical wavelet transform (EWT) and multiscale quantum entropy (MQE) to diagnose transformer faults. First, EWT is employed for partial discharge signal decomposition to get different IMF components and a residual. Secondly, the MQE sequence of each IMF is generated by signal decomposition. Then the dimension of the MQE sequence is reduced with the local tangent space arrangement algorithm (LTSA). Finally, a hierarchical clustering algorithm (HAC) is used for clustering analysis to get the recognition results of different types of discharge. Compared with different diagnostic methods, the effectiveness and superiority of the proposed method is verified by the simulation result and experimental data.
empirical wavelet transformation; multi-scale quantum entropy; partial discharge; transformer; hierarchical clustering
10.19783/j.cnki.pspc.211255
国家自然科学基金项目资助(SGLNDK00KJJS15 00008),东北电力大学博士科研基金项目资助(BSJXM201406)
This work is supported by the National Natural Science Foundation of China (No. SGLNDK00KJJS1500008).
2021-09-11;
2022-01-18
尚海昆(1984—),男,博士,副教授,研究方向为电气设备故障诊断;E-mail: shanghk@neepu.edu.cn
李宇才(1996—),男,通信作者,硕士,研究方向为电气设备故障诊断;E-mail: liyucai1781532811@163.com
林 伟(1997—),男,硕士,研究方向为电气设备故障诊断。E-mail: 2202000096@neepu.edu.cn
(编辑 魏小丽)

