2022年高考理综全国乙卷第25题赏析及启示

樊兰君

（陕西省西安中学，陕西 西安 710018）

自2019年《中国高考评价体系》发布后，近3年全国卷压轴题中，不论是2020 年Ⅱ卷的“管球”、2021年乙卷的“框棒”板块模型，还是2022年甲卷放大法观察微小形变求待测电流、2022年乙卷碰撞模型的考查，都是在进一步深化基础，强调要求学生全面深刻地理解和融会贯通地运用基础性知识.试题改变设问角度，创新考查方式方法，引导中学教学遵循教育规律，回归课标和教材，减少死记硬背和“机械刷题”.2022年是“双减”政策后的首次高考，试题命制要求在教考衔接上下功夫，有效服务“双减”，切实引导教学.现对2022年高考全国乙卷第25题进行深入分析，以管窥当前高考物理命题变化动向，也对今后物理教学提供有益参考，欢迎同行批评指正.

1 真题再现

例题.如图1（a），一质量为m 的物块A 与轻质弹簧连接，静止在光滑水平面上：物块B 向A 运动，t=0时与弹簧接触，到t=2t0时与弹簧分离，第1次碰撞结束，A、B 的v- t 图像如图1（b）所示.已知从t=0到t=t0时间内，物块A 运动的距离为0.36v0t0.A、B 分离后，A 滑上粗糙斜面，然后滑下，与一直在水平面上运动的B 再次碰撞，之后A 再次滑上斜面，达到的最高点与前一次相同.斜面倾角为θ（sinθ=0.6），与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求

图1

（1）第1 次碰撞过程中，弹簧弹性势能的最大值；

（2）第1 次碰撞过程中，弹簧压缩量的最大值；

（3）物块A 与斜面间的动摩擦因数.

2 试题赏析

本题属于学习问题探索类情境试题，试题文本简约，物理情境清晰明了，结合A、B 两物块的v- t图像更能考查学生提取信息的分析和推理能力，既遵循了物理学科的基本规律，又突出了对学生学科素养的考查.设问有合理梯度，有利于学生发挥正常水平，符合考试目的的要求.试题严格遵循《普通高中物理课程标准（2017年版）》中的命题建议：科学合理设计试题难度，根据物理学科核心素养的水平层次、试题情境的复杂性及新颖性、知识要求的深度及广度多方面设计试题难度.结合新课标中课程内容要求，抽取具有代表性的核心物理概念、规律、思想和方法等内容设计试题，试题的设问角度及方法要科学、可信、新颖、灵活.［1］

2.1 立足必备知识 凸显学科素养

本题涉及的必备知识及重要规律主要有：力和运动的关系、v- t 图像识图析图、牛顿运动定律、动量定理、动量守恒定律、动能定理、能量守恒定律等.这些都是高中物理的基础知识核心主干重要规律.

从核心素养方面本题注重考查物理观念，将运动和相互作用观念、能量观念、动量观念综合起来考查，是考查学生对概念和规律的提炼和升华.在科学思维和科学探究方面，本题考查碰撞模型中两类特殊的完全弹性碰撞和完全非弹性碰撞模型，要求学生经过模型建构和科学推理加上科学论证，结合函数图像数据分析，利用微元积累思想或积分方法、图像位移分割法求位移等等，使学生科学思维得到进一步升华.在科学态度与责任方面，通过不同思路切入一题多解，让学生感受物理学科思维的广阔度和灵活度，体会科学严谨的多样性，大大开阔学生的思维视野.

2.2 创新考查形式 强化关键能力

本题虽然以学生熟悉的、常规的两大碰撞模型、斜坡上物体往返运动为载体，但在基础性、综合性、应用性与创新性等方面进行了有效整合.在具体的情境中考查学生对物理本质的理解，引导学生知其然，更知其所以然，逐渐形成对物理全局性、整体性认识，避免将学生导向典型题套路和技巧的运用.［2］试题借助A、B 的v- t 图像从新的视角设置了对学生信息获取和数据分析的考查，尤其第（2）问的设问，初看针对两物体变速运动的相对位移无法从图像中直接获取，但需要学生打破思维定势，寻找新的角度去解决问题.在关键能力考查方面，第（3）问中A、B 两物块完全弹性碰撞两大守恒定律的联立求解，A 物块滑上斜面再返回3个过程中选取其中两个过程动能定理的联立求解，都对学生观察分析对比能力及数理运算能力有较高要求.

3 解题方法分析

3.1 第（1）问的解析

第（1）问解答方法相对单一，是学生最为常见的完全非弹性碰撞模型，很好切入.由图1（b）可知在t=t0此过程中B、A 及弹簧构成的系统动量守恒，机械能守恒，则B、A 发生碰撞，0 -t0时间内动量守恒mBvB=（mB+mA）v共，代入数据mB·1.2v0=（mB+m）·v0，解得mB=5m.t0时刻，A、B 系统动能损失最大，转化为弹性势能

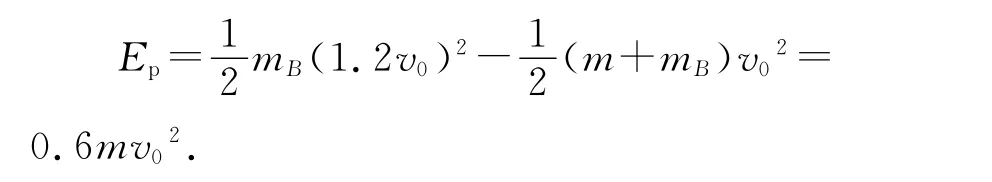
3.2 第（2）问的解析

第（2）问中，首先要理解清楚弹簧最大压缩量的物理意义，在A、B 物块均做变速运动过程中两者对地位移之差.有如下5种解法.

解法1：动力学观点，寻找等时前提下B 和A的加速度、速度与对地位移的关系.

解法2：平均动量守恒定律与平均速度和对地位移的关联.

0 t0时间内，A、B 和弹簧构成的系统动量守恒，有ΔpB=-ΔpA，即mB（1.2v0-vB）=mAvA.代入xA=0.36v0t0，得xB=1.128v0t0，则弹簧压缩量最大值Δx=xB-xA=0.768v0t0.

解法3：微元累加法.

在0- t0过程，由动量守恒定律知mAvA+mBvB=（mB+mA）v共，两边同乘以时间t，得mAvA·t+mBvB·t=（mB+mA）v共·t，在t0时间内，累积求和可得mxA+5mxB=6mv0t0，又因xA=0.36v0t0，解得xB=1.128v0t0，则弹簧压缩量的最大值Δx=xB-xA=0.768v0t0.

解法4：v- t图像面积法.

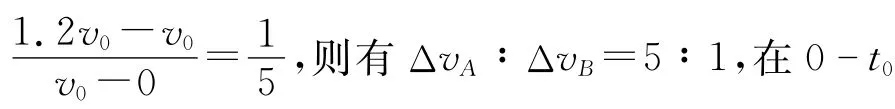
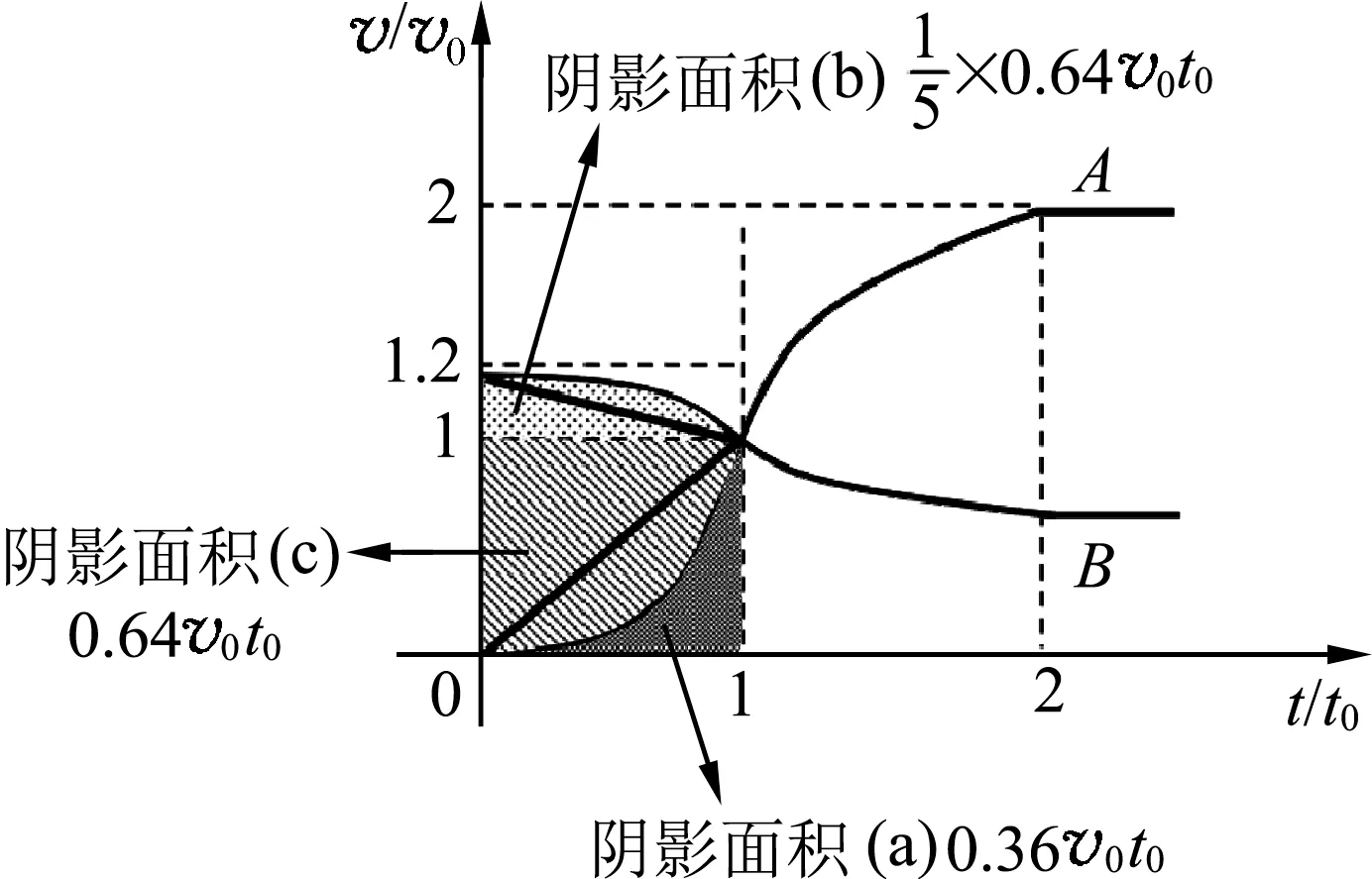
图2

常见错解：物块B 和物块A 发生弹性碰撞，弹簧弹力分别对物块A 做正功，对物块B 做负功，弹力做的总功即对应弹性势能的变化.由于弹簧弹力是线性变力，所以可以用平均力计算弹力做功.对物块A 而言，弹力做正功为·xA=，对物块B 而言，弹力做负功为-·故弹簧压缩量的最大为Δx=xB-

错解反思：任何时刻，A、B 的弹力大小总相等，力在时间上的积累效应相同，但力做功反映的是力在空间上的积累效应，由于物块A 和物块B 各自发生的作用点位移不同，因此各自位移对应的平均力¯F 不同，故无法利用功能关系求解.

3.3 第（3）问的解析

第（3）问A、B 发生第2次碰撞属于完全弹性碰撞模型，关键在于注意矢量性和系统动量守恒和机械能守恒两个方程的求解技法（代入法在考场不适合）.A 从斜坡滑上滑下时两个子过程一个整过程中对A 用动能定理或运动学规律的应用.第2次碰撞过程A、B 系统动量守恒，动能守恒

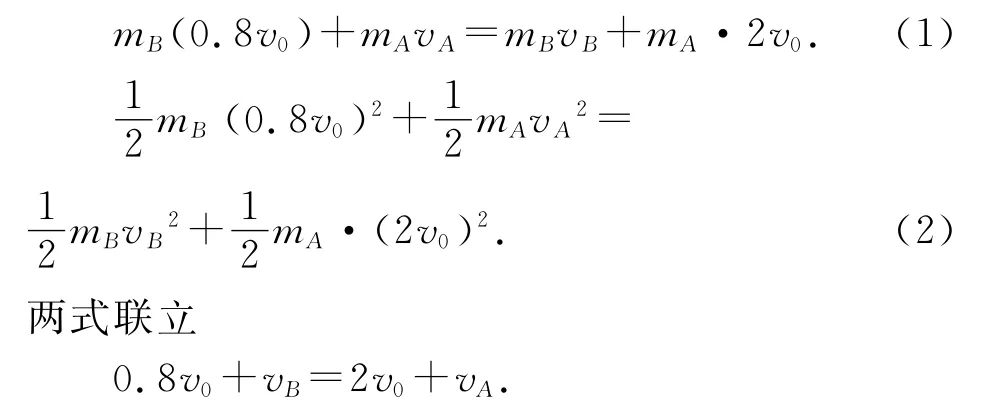
代入得动量守恒表达式A 从斜面上滑下时速度vA=-v0，此后A 在斜坡上的运动可采取不同解法.

解法1：功能关系，动能定理求解.

设第1次碰撞后A 在斜面上上升的最远距离为x，则上升至最高点

4 教学启示

一道高考题的设计是经过命题专家深思熟虑的，经典模型不按“套路”出牌常考常新将是新高考试题的亮点.这就要求教师在教学中落实新课标要求，深挖教材编者意图，保证学生必备基础知识和核心规律的牢固与完备，在坚实的概念性知识和程序性知识做保障的前提下，让学生熟练掌握通用性的物理方法，训练学生思维的广阔性和灵活性.教学中要对教材中的典型例题和课后习题多进行“一题多解、一题多变、多题归一”的变式训练，［3］让学生能够吃透题目信息本质，通过自主独立思考和小组合作探究，挖掘学生潜力激发学生相互的思维火花，引导学生在讨论分享中形成多样化的问题解决意识，既增强学生自信心，也提升学生课堂积极性和参与度.这样学生才能在新的命题情境和设问方式中明确思维去向，快速找到解决问题的突破口，避免“死记硬背、机械刷题”的现象.