基于改进RRT算法的猕猴桃采摘机器人全局路径规划

崔永杰 王寅初 何 智,3 曹丹丹 马 利 李 凯,3

(1.西北农林科技大学机械与电子工程学院，陕西杨凌 712100；2.农业农村部农业物联网重点实验室，陕西杨凌 712100；3.陕西省农业信息感知与智能服务重点实验室，陕西杨凌 712100)

0 引言

路径规划是猕猴桃采摘机器人的关键技术之一，主要分为基于地图环境已知的全局路径规划和基于传感器信息的局部路径规划[1-3]。全局路径规划主要包括寻找一条将起始点和目标点连接同时避免与障碍物发生碰撞的路径，其路径长短、算法时间和空间复杂度是评判全局路径规划算法性能的主要指标[4-6]。常见的全局路径规划算法有A*算法、RRT算法、遗传算法等[7-9]。其中由LAVALLE[10]提出的RRT算法概率完备、结构简单且具有灵活的搜索能力，适用于各种复杂环境下的路径规划，但因其随机采样的机制而存在节点利用率低、路径复杂度高且收敛速度慢等问题[11-13]。

针对RRT算法存在的不足，学者们提出多种改进方法，文献[14]提出目标引力-RRT算法，将人工势场法中的引力思想融入RRT算法，通过采样节点与目标点的共同引力作用影响随机树的扩展，增强了节点扩展过程中的目标偏向性，有效提高了路径的搜索效率和收敛速度。文献[15]提出RRT-Connect算法，该算法基于构造两个快速搜索随机树分别从起始点和目标点生长，双向生长特性有效缩短了算法收敛时间。文献[16]提出RRT*算法，在随机树节点扩展过程中引入了随机几何图与剪枝优化理论，保证了该算法的渐进最优性，极大降低了算法路径复杂度。文献[17]提出的Quick-RRT*算法，利用三角不等式原理改进RRT*父节点选择和重新布线的方式，提高了初始路径的质量和收敛到最优解的速度[18-19]。

本文针对传统RRT算法搜索效率低、收敛速度慢且路径复杂度高等问题，提出一种基于采样状态实时引导随机树扩展的改进方法。首先引入评价指数与阈值实时划分随机树的采样状态，根据采样状态决定采样节点的选取方式，实时引导随机树的扩展，避免随机树的盲目探索。其次，为增强算法对不同环境的自适应性及快速避开不规则障碍物，引入动态阈值及改进最近节点选择机制。最后对路径进行优化处理，得到平滑且复杂度低的路径。

1 算法原理

1.1 问题描述

定义X=Rd为配置空间，Xobs∈X为障碍空间、Xfree∈X为无障碍空间，xinit∈Xfree为起始点，xgoal∈Xfree为目标点。‖x1,x2‖为配置空间X中节点x1、x2的标准欧氏距离，设路径β:[0,1]∈X为一有界变化函数。τ为路径β上的点，如果∀τ∈[0,1],β(τ)∈Xfree则路径β为可行路径。

问题1：在给定的条件(Xfree，xinit，xgoal)下寻找一条可行路径，其中β:[0,1] →Xfree,β(0)=xinit且β(1)=xgoal。

问题2：在给定的条件(Xfree，xinit，xgoal)下在最短的时间t内找到可行路径β:[0,1]。

1.2 RRT算法

RRT算法基于构造一棵随机采样并逐步扩展的无冲突路径树，从起始点寻找目标点[20]。随机树以起始点xinit为根节点，在每次迭代中从配置空间X中随机选取一个采样节点xrand，搜索随机树中的所有节点并找到距离xrand最近的节点记为xnearest。以xnearest为起点沿着xnearest和xrand的方向以一个特定的步长创建一个新节点xnew，如果xnew∈Xfree且xnew和xnearest之间的连线σ∈Xfree，则将xnew添加到随机树中，并将xnearest作为它的父节点。计算每一个新节点与目标点的距离，如果小于设定的值且两点的连线与障碍物无碰撞则认为找到路径，将新节点与目标点相连，通过从目标点回溯到起始点来绘制路径，否则重复上述搜索过程。

2 改进RRT算法

2.1 评价指数

Straight-RRT将生成的新节点分为两类，分别是向着目标收敛的新节点和趋于探索的新节点。设评价指数U初始值为1，实数i、e为评价指数增、减量，每当新节点加入随机树中计算新节点xnew与目标点xgoal的欧氏距离d=‖xnew,xgoal‖，如果新节点不是当前随机树中最接近目标点的节点(如图1a所示)，则认为该新节点是趋于探索的新节点，评价指数加i，否则认为是向着目标收敛的新节点，如图1b所示，评价指数减e。评价指数可以实时反映随机树当前的探索情况，评价指数越大表示在当前阶段内随机树向着未知区域探索的点占比越大，向着目标收敛的点占比越小。

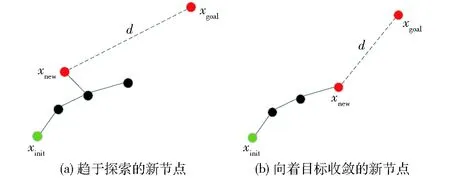
图1 评价指数Fig.1 Evaluation index

2.2 扩展阶段划分

设定初始阈值为一常数a，根据评价指数是否达到阈值将随机树的扩展过程分为探索阶段和收敛阶段。当评价指数小于阈值时，随机树为探索阶段，采样节点依旧为自由空间内随机点，如图2a所示。随着迭代次数的增加，当评价指数的值达到阈值时，说明该阶段趋于探索的点占比过大，随机树进入收敛阶段，在收敛阶段随机树以目标点作为采样节点进行扩展，如图2b所示。直至与障碍物发生碰撞，随机树结束收敛阶段，如图2c所示。随后评价指数回到初始值1，随机树重新回到探索阶段，如图2d所示，当评价指数下一次达到阈值时随机树会再次进入收敛阶段。通过探索和收敛阶段的不断转换，使随机树在扩展过程中能够根据当前的探索情况实时修正采样节点的采样位置，减少盲目探索，提高算法的收敛速度。

图2 探索及收敛阶段Fig.2 Exploration and convergence phase

2.3 改进收敛阶段最近节点选择机制

每当随机树结束一次收敛阶段时，将开始进入收敛阶段时的最近节点xnearest以及在此次收敛阶段扩展的新节点xnew记录到点集R中，下一次随机树进入收敛阶段将不会选择点集R中的点作为最近节点xnearest。

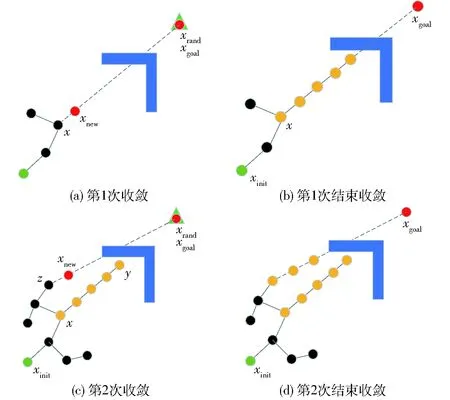
图3 收敛阶段最近节点选择Fig.3 Selection of the nearest node in convergence stage

如图3a所示，评价指数达到阈值随机树进入收敛阶段，随机树以节点x为最近节点向着目标点扩展，直到与障碍物发生碰撞，随机树结束收敛阶段，将节点x以及在此次收敛阶段扩展的新节点记录在点集R中，如图3b所示(点集R中的点被标记为黄色)。当评价指数达到阈值随机树再一次进入收敛阶段时如图3c所示，虽然节点y距离采样点最近，但在收敛阶段时点集R中的点不会被选为最近节点xnearest，所以点z作为最近节点xnearest向着目标方向扩展，直至与障碍物发生碰撞结束收敛阶段，将点z以及此次收敛阶段扩展的新节点记录到点集R中，如图3d所示。通过改进收敛阶段的最近节点选择机制可避免在收敛阶段以重复的点作为最近节点，从而更快地避开不规则障碍，加快算法收敛速度。

2.4 动态阈值设定

Straight-RRT通过评价指数是否达到阈值来判断当前随机树的扩展情况从而调整采样方式，对于简单的环境，不需要随机树进行过多的探索所以较小的阈值可以更快地找到路径，对于障碍物较多的复杂环境需要更大的阈值以便随机树对环境进行足够的探索。为了使算法适应各种环境，本文引入动态阈值，将随机树进入收敛阶段的次数作为实时评判环境复杂度的标准，阈值T随着随机树的探索过程进行自适应调整，阈值T表达式为

T=a+n

(1)

式中n——当前随机树进入收敛阶段的次数

如图4a所示，当前随机树进入收敛阶段的次数为1，则当前阈值为T=a+1，如图4b所示，随机树进入收敛阶段的次数为2，则当前阈值为T=a+2。动态阈值在随机树扩展过程中实时变化使随机树在复杂的环境下能够进行足够的探索，从而提高算法对不同环境的自适应性。

图4 动态阈值Fig.4 Dynamic threshold

2.5 路径优化

RRT算法因其随机采样的特性导致其规划的路径产生较多冗余点，需要对其进行优化处理降低路径复杂度[21]。首先将路径起始点作为修剪起始点，依次检测路径后续节点与修剪起始点相连是否与障碍物发生碰撞，如果无碰撞则删除两节点之间的路径节点并直接将两节点相连，随后将新得到的路径中的第2个点作为修剪起始点，再次执行上述操作，直至目标点成为修剪起始点，结束修剪过程得到最终路径。如图5a所示，初始路径为1-2-3-4-5-6-7-8-9，修剪后路径为1-5-7-9。但修剪后路径依旧存在转折点，为使路径更加平滑，对路径上每个转折点处进行二次贝塞尔曲线拟合，定义拟合空间n+1个点的位置Pi(i=0,1,2,…,n)，则n次贝塞尔曲线表达式为

(2)

其中

(3)

式中Pi——贝塞尔曲线的控制点

α——贝塞尔曲线参数

Bi,n(α)——n次Bernstein基函数

图5 路径优化示意图Fig.5 Schematic of path optimization

因二次贝塞尔曲线需3个点进行拟合，为了保持拟合曲线和原轨迹曲线一致性，如图5b所示，设每个转折点为P1，在转折点两侧线段上分别选取两点P0及P2作为贝塞尔曲线的控制点，且两点与转折点的距离为其所在线段长度的1/10，对每处转折点进行二次贝塞尔曲线拟合，最后将多段贝塞尔曲线进行拼接，得到一条复杂度低且平滑的路径。

3 算法仿真与实验

3.1 不同环境下仿真实验

为验证改进算法的有效性，将Straight-RRT算法与RRT算法、文献[14]中的目标引力-RRT算法(引力系数取0.5)、RRT-Connect算法在如图6所示环境下进行对比仿真实验，仿真实验中对4种算法均进行路径优化处理，4种算法搜索步长取2，Straight-RRT初始阈值a取5，评价指数增、减量i、e分别取1、0.5，地图1、2、3规模均为[70，70]，在3种环境下每种算法分别进行100次独立运行。算法运行环境为64 bit Windows 10，处理器Intel(R) Core(TM) i5-6300HQ，内存4 GB。

如图6所示，地图1为障碍物相对较少的环境，用于检验算法在简单环境下的搜索能力，起始点位置为[5,35],目标点位置为[65,35],地图2为多障碍物排列杂乱的环境，用于检验算法在多障碍物环境下的搜索能力，起始点位置为[5，5],目标点位置为[65，65]，地图3为迷宫环境，地图起始点位置为[15，7],目标点位置为[65，65]。算法运行效果如图7～9所示。从图7～9可以看出，4种算法均能完成起始点到目标点的全局路径规划，且经过路径优化处理后均能获得较为平滑的路径。其中本文改进的Straight-RRT算法的采样节点数比其他算法明显减少，4种算法100次运行的平均搜索时间、平均迭代次数如表1所示。

从表1可以看出，在3种地图环境下Straight-RRT的搜索时间及迭代次数均小于其他规划算法，在地图1环境下Straight-RRT算法相比于RRT算法、目标引力-RRT算法及RRT-Connect算法的平均搜索速度分别提升了88.23%、74.35%、16.66%，迭代次数缩减了65.77%、49.53%、38.76%。地图2环境下平均搜索速度分别提升90.35%、74.11%、12.00%，迭代次数缩减77.15%、60.82%、27.10%。地图3环境下平均搜索速度分别提升79.38%、49.15%、25.30%，迭代次数缩减52.51%、40.76%、40.35%。4种算法的初始路径及路径优化后的路径长度如表2所示。4种算法在不同地图环境下，总体初始路径的平均长度分别为97.71、109.29、122.50，优化后路径的平均长度为77.00、93.61、100.30，平均路径缩减了21.19%、14.34%、18.12%。进一步说明了路径优化有效地减小了4种算法初始路径的复杂度。

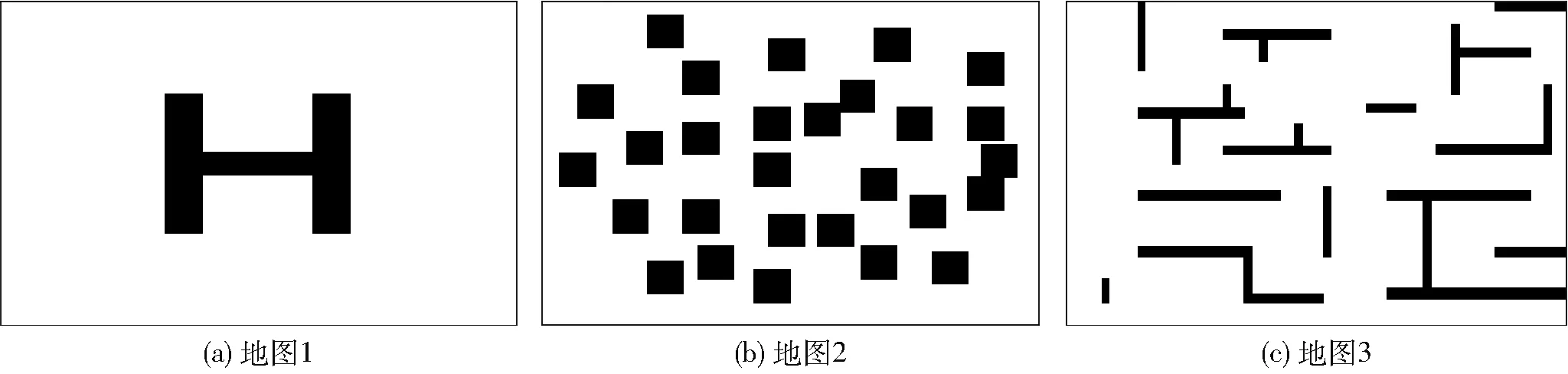
图6 仿真环境Fig.6 Simulation environment

图7 地图1算法运行效果Fig.7 Algorithm operation effect of map 1

图8 地图2算法运行效果Fig.8 Algorithm operation effect of map 2

图9 地图3算法运行效果Fig.9 Algorithm operation effect of map 3

表1 不同环境下算法仿真结果Tab.1 Algorithm simulation results in different environments

表2 路径优化前后对比结果Tab.2 Comparison results before and after path optimization

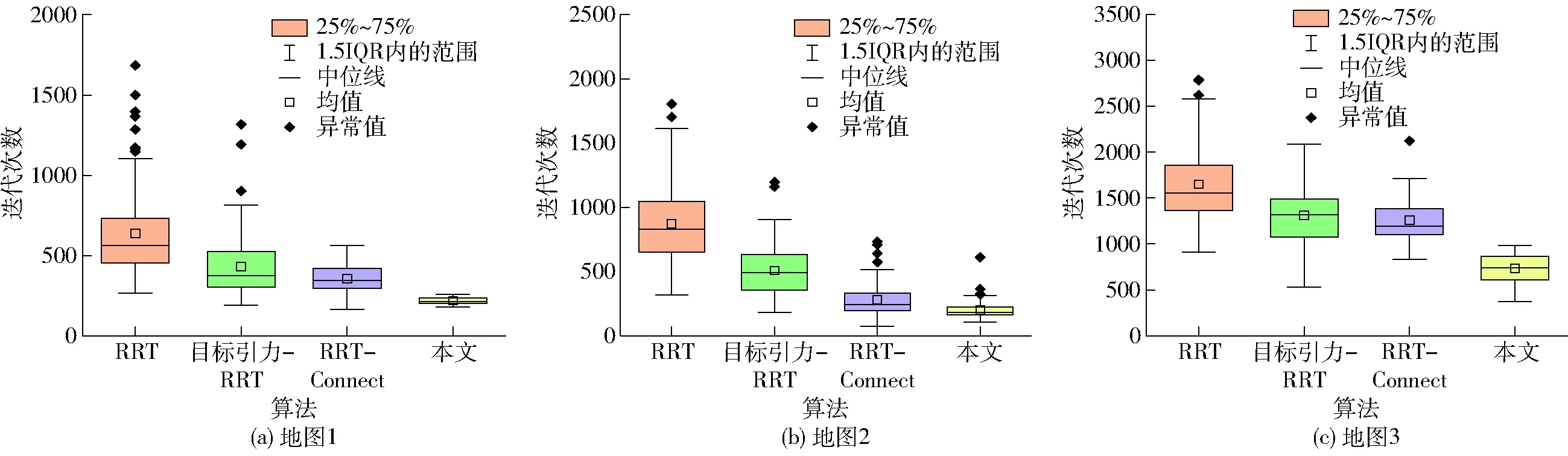
图10 迭代次数箱线图Fig.10 Number of iterations boxplot

4种算法100次仿真实验中迭代次数如图10所示。从图10可以看出，本文算法在保持更少迭代次数的同时，分布结果也较为集中。综合上述仿真实验可知，本文改进的Straight-RRT算法有效地提高了RRT算法的收敛速度、路径质量及稳定性。

3.2 猕猴桃果园环境场地实验

基于西北农林科技大学眉县猕猴桃试验站环境进行路径规划实验，果园为棚架式种植模式，内部环境如图11所示，横向间隔为4 m，列向间隔2 m，高1.8 m，为避免猕猴桃采摘机器人行至地膜区域，将地膜区域设为障碍物，此外为保证机器人安全移动，对障碍物边界进行膨胀处理，二维环境地图如图12所示，图中黑色区域为障碍物区域，蓝色区域为膨胀区域。

图11 眉县猕猴桃试验站环境Fig.11 Environment of Meixian kiwifruit test station

图12 猕猴桃果园二维地图Fig.12 Two-dimensional map of kiwifruit orchard

猕猴桃采摘机器人如图13所示，由履带式移动底盘搭载6自由度UR5机械臂组成，机械臂工作空间为半径0.85 m的半球区域，机械臂底座高度为1.1 m。结合棚架高度，计算出猕猴桃采摘机器人实际有效采摘区域为图14中左侧所示的黄色区域，将该区域投影至二维平面，计算出有效采摘区域在二维平面的投影为一个半径为0.48 m的圆形区域，其最大内接正方形边长为0.68 m，见图14右侧。

图13 猕猴桃采摘机器人Fig.13 Kiwifruit harvesting robot

图14 猕猴桃采摘机器人有效采摘区域Fig.14 Effective harvesting area of kiwifruit harvesting robot1.履带式移动底盘 2.机械臂工作空间 3.棚架 4.有效采摘区域 5.UR5机械臂 6.有效采摘区域二维平面投影 7.有效采摘区域二维平面投影的最大内接正方形

为实现猕猴桃采摘机器人有效采摘区域对猕猴桃果园的全覆盖，对猕猴桃果园进行分区处理。将果园每个行间区域设置为单独的工作区，在每个工作区内，取猕猴桃采摘机器人有效采摘区域二维平面投影的最大内接正方形，依次排布直至铺满整个工作区，并依次进行编号，如图15所示。其中每个正方形区域的中心点即为采摘机器人的一个导航目标点，在一个工作区内，猕猴桃采摘机器人以1号点为起始点，按编号顺序依次经过该工作区内所有导航目标点后，随后移动到下一个工作区的1号点，继续按编号依次遍历每个导航点，直至遍历所有工作区的导航目标点，则认为猕猴桃采摘机器人的有效采摘区域完成了对猕猴桃果园的全覆盖。

选取2个工作区进行路径规划实验，为验证算法对复杂环境的适应性，对工作区1随机增加一些障碍物。地图环境如图16a所示，红色点为一个工作区中的起始导航点，绿色点为最终导航点，黄色点为猕猴桃采摘机器人需要依次经过的中间导航点。采用本文算法在此地图环境下进行路径规划实验，路径规划效果如图16b所示，其中红色线段、蓝色线段、紫色线段分别为猕猴桃采摘机器人在工作区1、工作区2、工作区间的规划路径。从图16可以看出，规划路径从工作区1的起始导航点开始依次遍历了每一个导航点，同时具有较低的路径复杂度，可以实现猕猴桃采摘机器人有效采摘区域对猕猴桃果园的全覆盖。

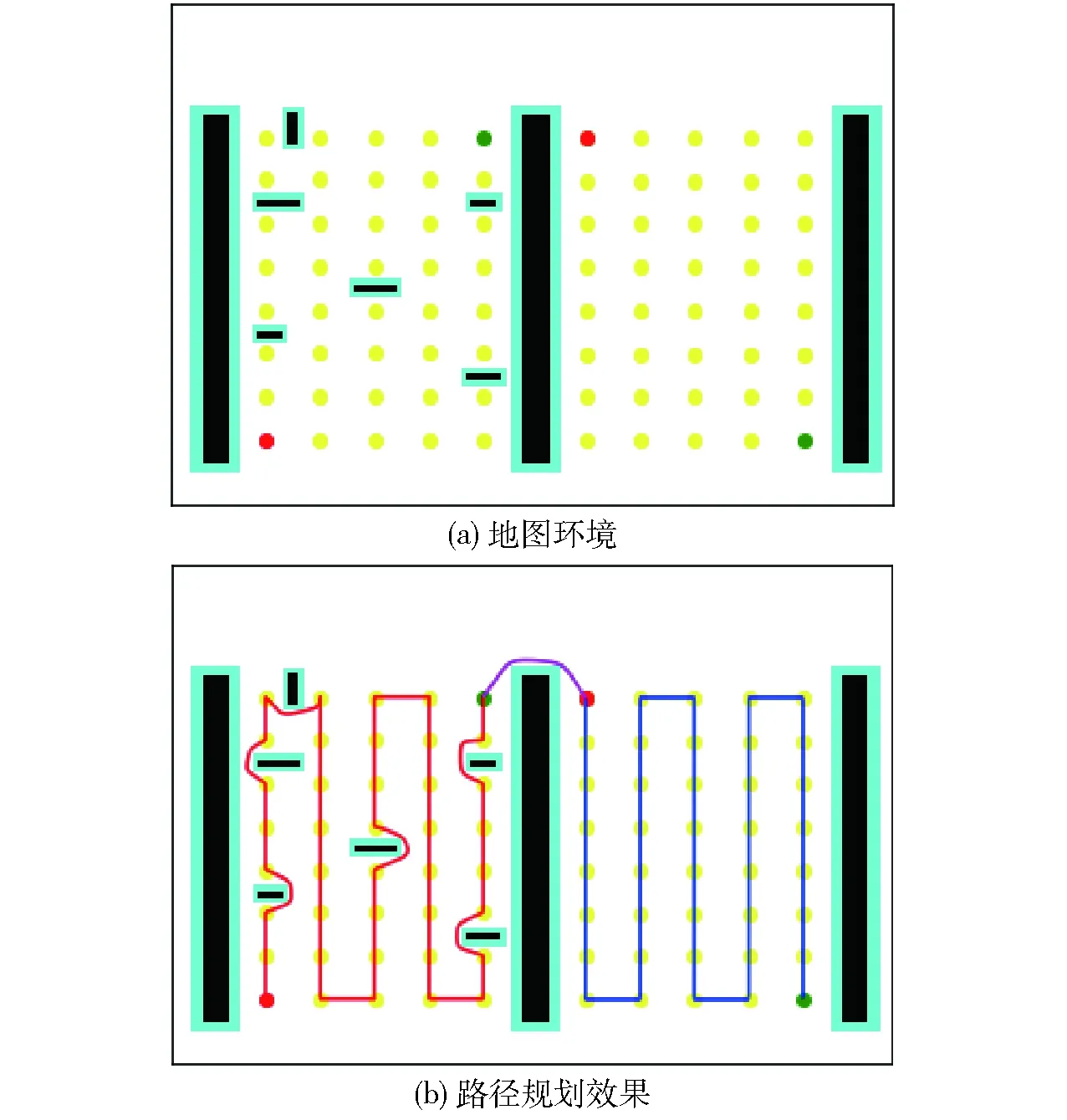
图16 地图环境及路径规划效果Fig.16 Map environment and path planning effect

使用RRT算法、目标引力-RRT算法、RRT-Connect算法分别在此地图环境下进行路径规划实验，总路径及工作区1、工作区2、工作区间路径规划结果如表3所示。

表3 猕猴桃果园环境路径规划结果Tab.3 Planning results of environmental paths in kiwifruit orchards

在工作区1中，本文算法搜索时间相比于其他3种算法分别缩减了73.67%、54.69%、27.46%，说明本文算法在工作区中存在障碍物的情况下具有更强的适应性及搜索能力。由于工作区2中不存在障碍物，4种算法在工作区2中的搜索效率均大幅提升，除RRT算法外其他3种算法搜索时间均保持在0.5 s以内。工作区间路径为从工作区1的最终导航点到工作区2的起始导航点的路径，在工作区间路径中4种算法的平均搜索时间为0.262 s，本文算法相比于平均搜索时间缩短了31.67%，说明本文算法在工作区间的路径规划上具有更高的搜索效率。从总体路径来看，本文算法的搜索时间相比其他3种算法分别缩减了74.31%、46.28%、26.60%，迭代次数缩减了86.52%、68.85%、29.23%。实验结果表明本文改进算法在猕猴桃果园环境中具有更好的适应性及规划效率。

4 结论

(1)引入评价指数，通过对新节点的分类实时更新评价指数。基于评价指数与阈值划分采样阶段，通过改变不同阶段的采样策略实时引导随机树的扩展。

(2)优化收敛阶段的最近节点选择机制，使随机树更快避开不规则障碍物。

(3)引入动态阈值，阈值随着环境复杂度实时调整，提高算法对不同环境的自适应性。

(4)对路径进行优化处理，去除路径冗余点并对路径进行二次贝塞尔曲线拟合。

(5)基于棚架式猕猴桃果园环境进行路径规划实验，本文改进算法在猕猴桃果园环境下搜索时间为1.208 s，相比RRT算法、目标引力-RRT算法及RRT-Connect算法分别缩减了74.31%、46.28%、26.60%，实验结果表明本文改进算法在猕猴桃果园环境中具有良好的适应性及规划效率。