基于概率犹豫模糊语言的航海类高校实验室评价
王志平, 傅 敏, 王沛文
(大连海事大学 a. 理学院; b. 航运经济与管理学院, 辽宁 大连 116026)
0 引 言
针对“十二五”中国航海教育发展情况开展调查研究,获得了较为翔实的基础数据。经过梳理统计,分析影响中国航海教育发展的诸多因素并提出了更新和转变航海教育理念,遵守教育规律以促进航海教育可持续发展。为了适应国家发展的需要,航海类人才培养成为航海类高校的重任。为了更好满足航运发展需要,迎合国家提倡的实践与理论相结合的发展观念,航海类高校的实验室建设、管理以及教学必须满足高质量、高层次、高水平的综合发展要求。无论从国家长远发展需求还是从航海类高校实验教学特点的角度,科研能力和实践能力的培养都是人才培养过程中的重中之重。为了高质量、高水平、高层次地完成国之重任,同时提高学校的科研水平以及办学实力,高校实验室建设成为首要任务。实验室的综合评价作为高校实验室建设与管理的一项重要内容,进一步促使实验室建设更高效高质量地完成[1-2]。
对高校实验室进行评价最重要的是对评价方法的选择。至今,越来越多的学者致力于高校实验室的研究与探索。宁浩男等[3]基于博弈论与云物元分析的高校实验室的文化建设进行了评价探讨;李丽[4]建立的实验室评价模型用到了层次分析法和三角模糊数相结合的方法;阳富强等[5]等又提出了基于(ISM)解释结构模型和(ANP)网络层次分析法相结合的实验室评价模型;吴立荣等[6]提出了在模糊环境下对高校实验室进行综合风险评价;后来,刘晶晶等[7]对最优最劣法(BWM)进行改进,提出了新的高校化学实验室的评价模型,解决了实验室管理存在的一些安全问题;田夏[8]等提出了熵权法和层次分析法相结合的实验室评价模型,李浩等[9]也应用熵权法在模糊环境下进行了财经类高校实验室的评价研究。
综上所述,虽然学者们对高校实验室评价模型进行了很多创新性的研究并且也取得了一定的成果,但现在实验室评价研究的过程中还是存在一些问题或者跟实际情况相比还存在一定的距离:① 大部分学者对实验室评价过程中的指标权重计算大都采用层次分析法和熵权法。层次分析法计算过程缺乏指标之间的相互作用,结果受主观影响较大;而熵权法又只考虑客观计算,未能体现出决策者的经验以及主观偏好,因此决策结果没能综合考虑主客观结合运算;② 大多数学者对实验室进行评价时,均假定决策者完全理性,完全采用客观方法计算得出结果;再者由于决策信息模糊性较强,用实数很难描述给出量化分析,进而决策矩阵的计算存在困难。并且决策者在决策时往往会出现不确定的心理状态,模糊集的应用很显然已经无法完整地描述决策者对于不同属性评估值之间的犹豫徘徊。但是,后来提出的犹豫模糊元又无法刻画决策者对不同隶属度的偏好信息,从而导致对实验室评估信息的不完整描述。基于上述研究现状以及研究过程中存在的种种挑战,为全方面考虑航海类高校实验室评估的现实情况以及决策信息难以量化的特点,基于概率犹豫模糊语言环境下,选取能综合体现航海类高校实验室的建设水平的属性对各实验室进行评估。既考虑了专家对于各实验室不同属性的评估值之间的犹豫心理又体现了专家对不同隶属度的偏好信息,使决策矩阵最大化接近现实情况,使决策结果更具说服力;并在此基础上,应用群体决策一致性原则确定决策者权重,应用最小相对熵原理进行主客观相结合的属性权重计算,避免了单一方法求解的局限性,使决策中的整个赋权过程合理可行;并基于前景理论采用VIKOR方法对备选方案进行综合排序择优;最后基于此模型用实例证明了所提模型的科学合理性。
1 相关理论基础
1.1 概率犹豫模糊术语集及相关知识
定义1[10]给定任意非空集合X,则定义在有限集合X上的一个概率犹豫模糊集可以表示为:
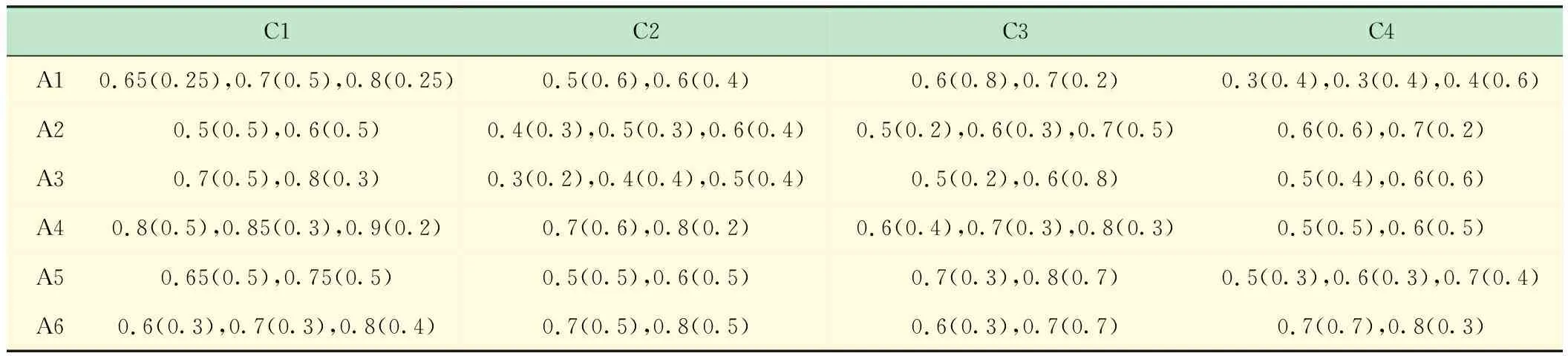
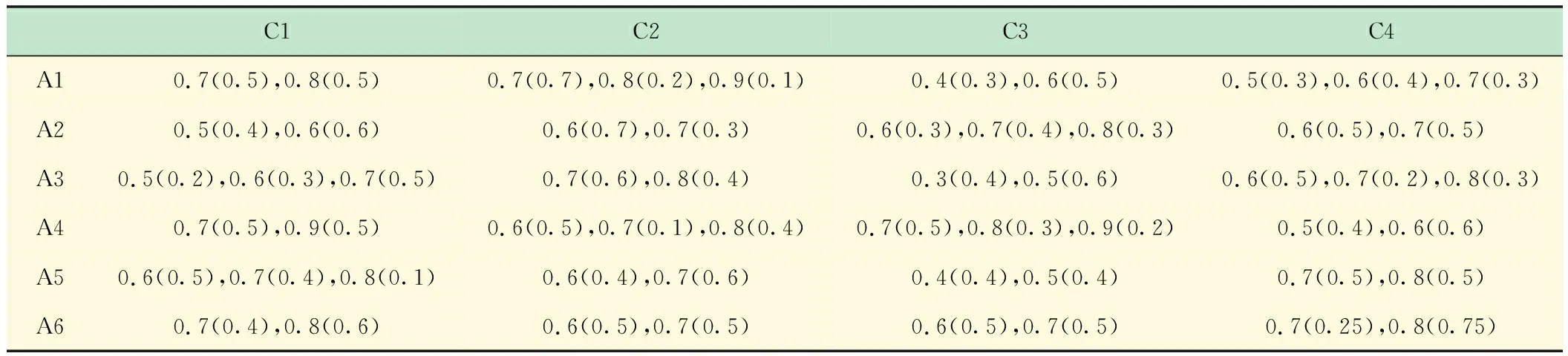
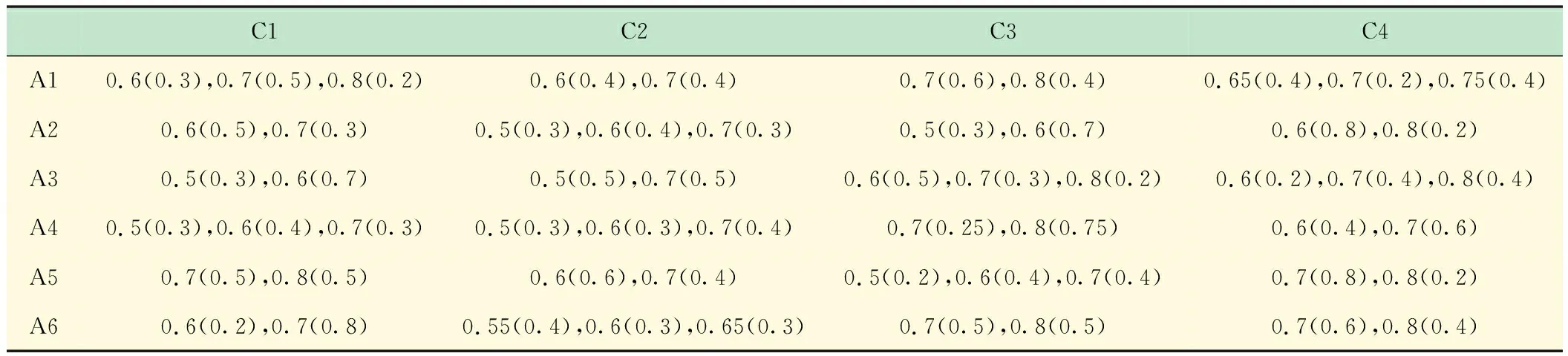
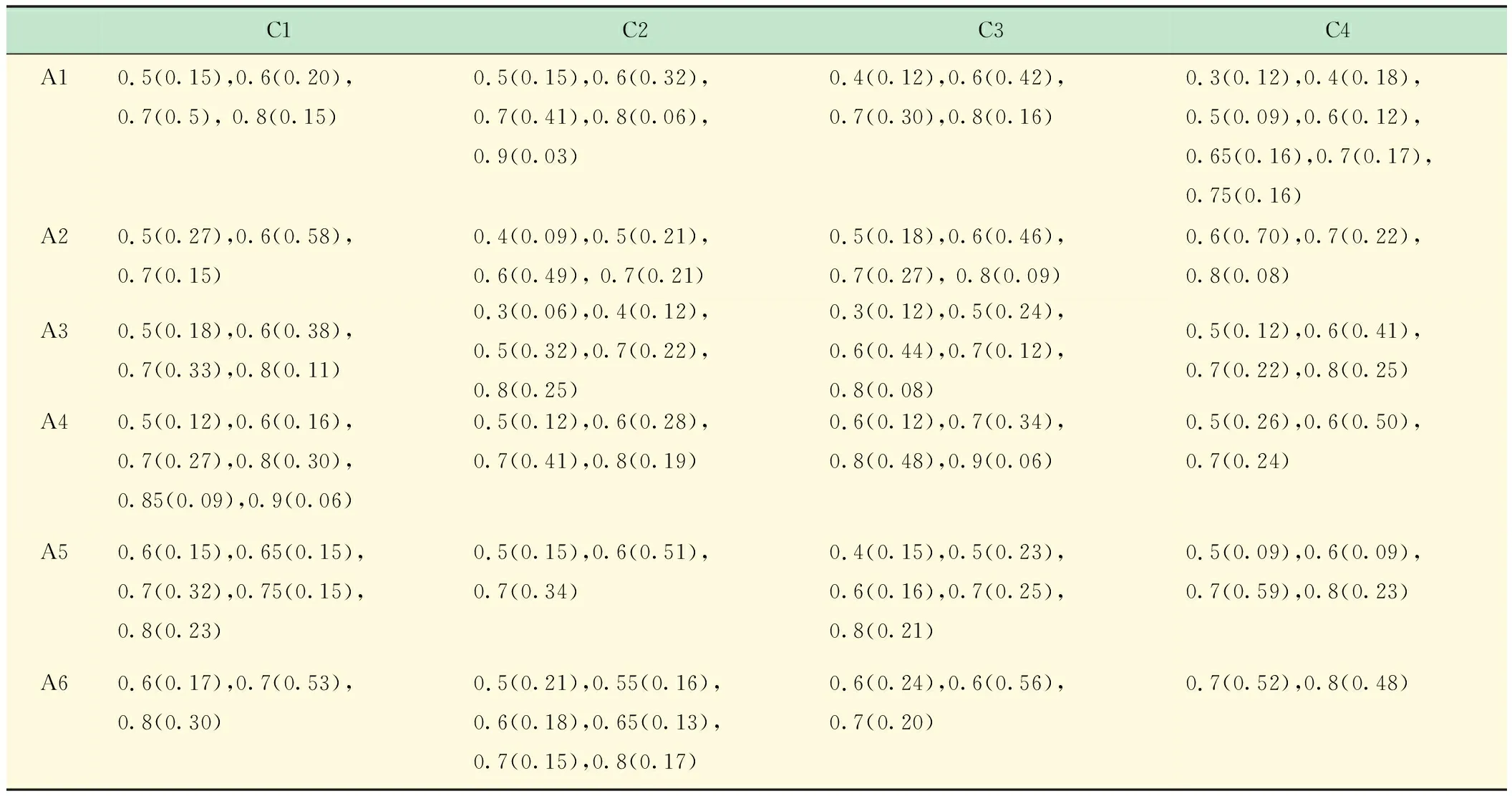
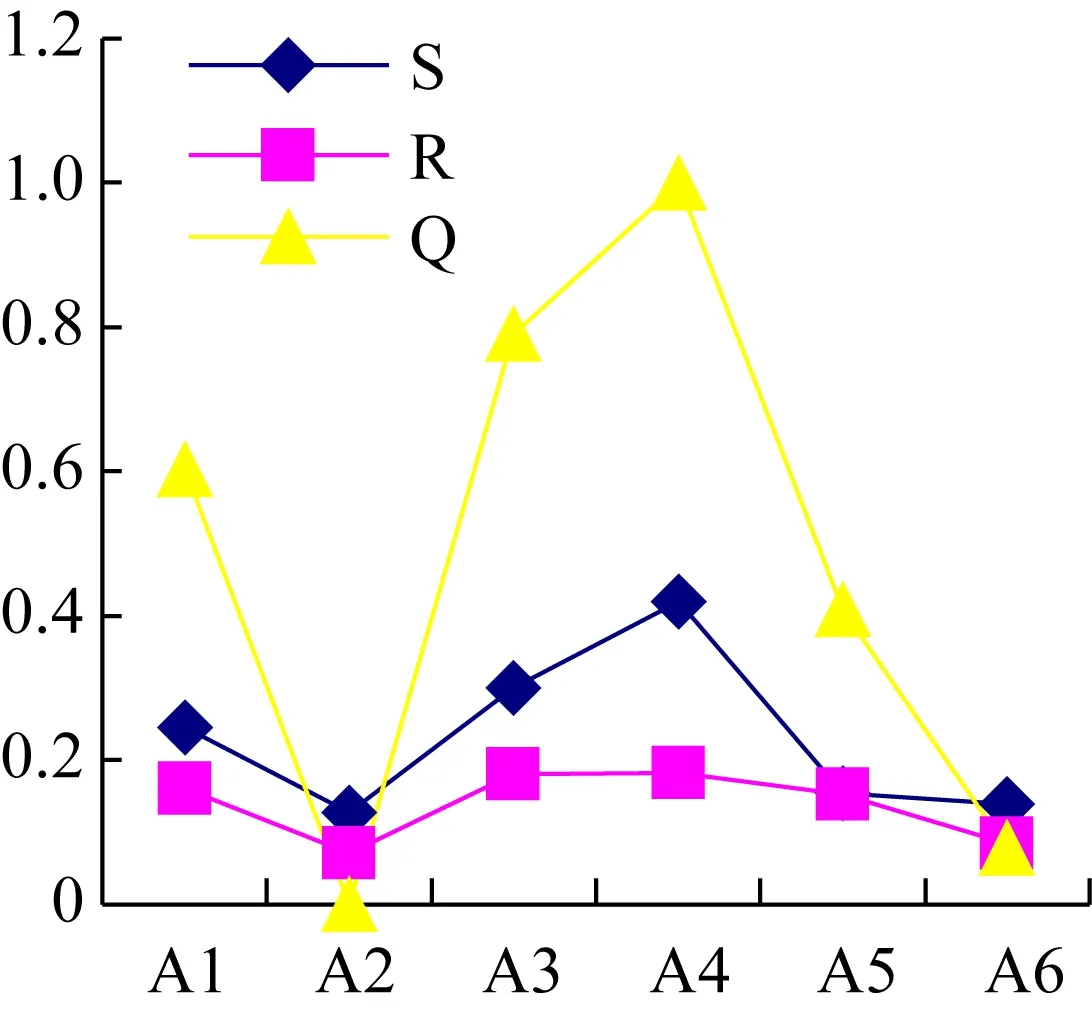
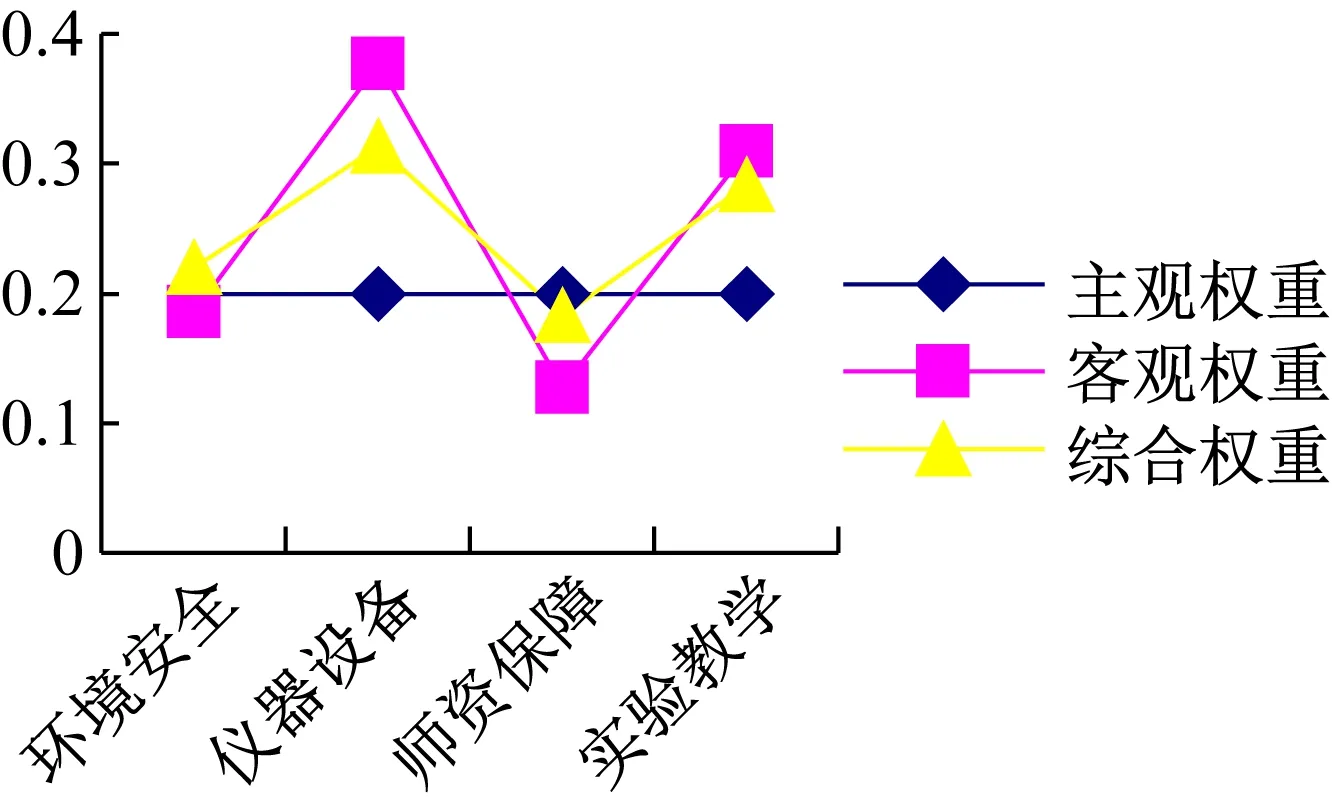
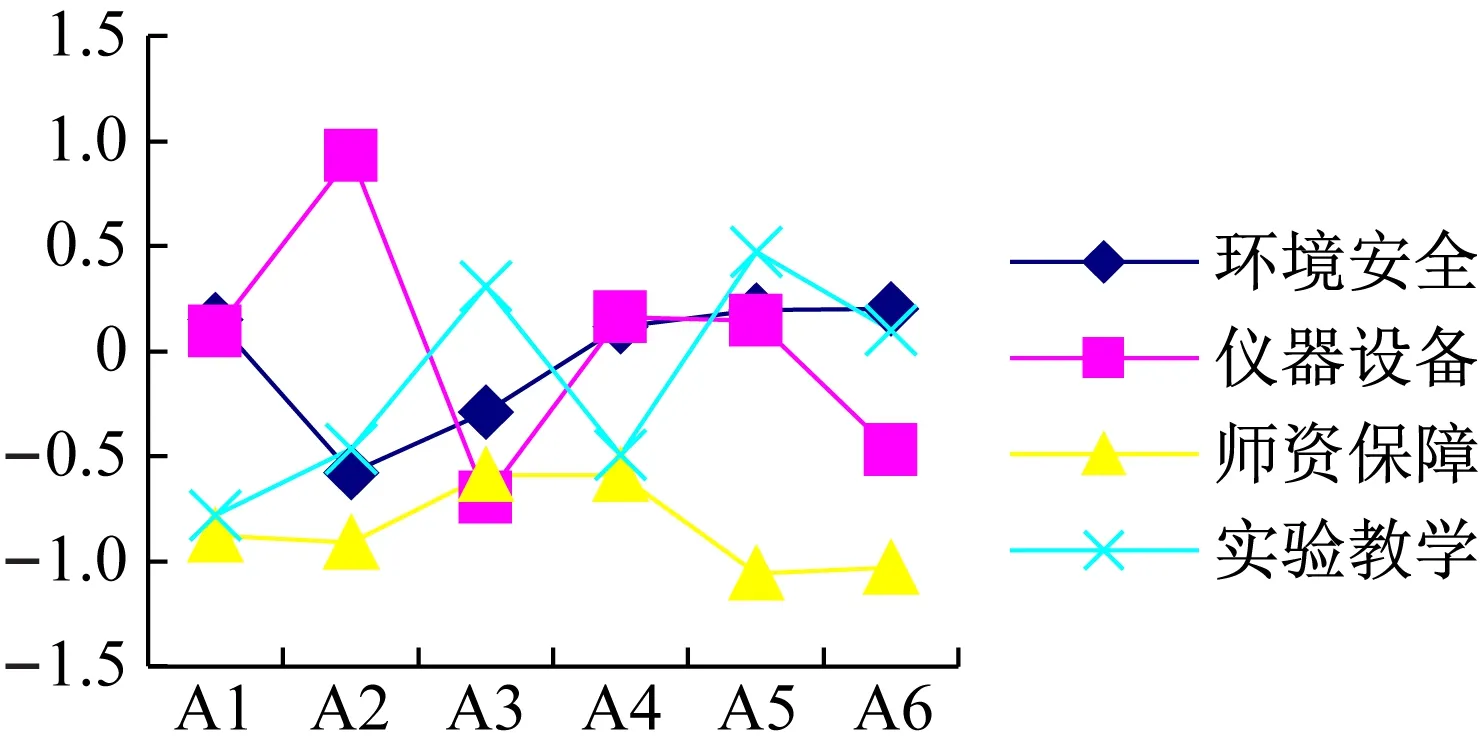
H={ (1) (2) (3) 定义4[11],设h1(p)和h2(p)是两个概率犹豫模糊集,如果他们两个的元素数量相同,则#h1=#h2=#h,同时给出两个概率犹豫模糊集的距离测度公式为: (4) 定义5[11]设是一个概率犹豫模糊集,其得分函数定义为: (5) 基于得分函数,其偏差度函数可以定义为: (6) 在得分函数和偏差度函数的基础上,任意两个概率犹豫模糊元h1(p1)和h2(p2)可按照以下原则进行比较: (1) 如果s1(h(p1))≻s2(h(p2)),则h1(p1)≻h2(p2); (2) 如果s1(h(p1))s2(h(p2)),则h1(p1)h2(p2); (3) 如果s1(h(p1))=s2(h(p2))并且d1(h(p1))≻d1(h(p1)),则h1(p1)h2(p2); 若s1(h(p1))=s2(h(p2))并且d1(h(p1))=d1(h(p1)), 则h1(p1)~h2(p2);若s1(h(p1))=s2(h(p2))并且d1(h(p1))d1(h(p1)),则h1(p1)h2(p2)。 前景理论[10],又称效用理论,是考虑决策者在决策过程中的不完全理性的心理行为。一般认为,前景价值越大,备选方案越好。前景值的大小表现在价值函数v(△x)的大小,即与参考点的偏差程度,表示决策者的心理行为,其公式为: (7) 式中,△x表示收益或者损失值,也就是与参考点的差值。△x≥0就表示决策点超出参考点的值,反之亦然。α和β分别表示了决策者对收益和损失的敏感系数,满足α0和β≻1。α和β的值越大,表明决策者愿意承担的风险越大;θ表示决策者对损失和收益的风险敏感性;θ≻1表示决策者对损失更敏感,依据研究可知,一般情况下,V(0)=0,α=β=0.88,θ=2.25。 前景理论值是基于每个备选方案距离参考点的收益或损失的距离。因此,前景理论的关键是选择一个合适的参考点,通常情况下,选取数据的中间值、期望、积极和消极的解作为理想参考点。 为了使决策结果尽可能的接近事实,考虑到直接给出决策者权重主观性太强,同时可以降低专家在地位、受教育程度、相关经验以及知识了解水平等方面对决策信息带来的非公正影响,MAO等[12]提出了对决策者权重进行重新调节的解决方法。依据不同决策者给出的不同决策信息,结合主观赋权和客观计算的方式得到相应的决策者权重调节系数,如果决策者的评价信息一致时,则给出拥有更高地位、经验更丰富以及知识水平更高的决策者dk更高的调节系数;否则当评价信息不一致时,那么相应的权重调节系数较低。 (8) (9) 很显然,ρk表示的是决策者dk与其他决策者的一致性程度,也就是说决策者dk提供的评价信息在整个评价小组中的受支持程度。同时反映了决策者dk的重要性。在某种程度上来讲,如果dk越重要,相应的调节系数ρk越大,那么决策者dk权重应当适当增加。因此,由事先赋予的主观决策者权重ηk和调节系数ρk来最终确定决策者权重: (10) 对于属性权重的确定,构造了两个优化模型来获得客观属性的权值和整体属性的权值。首先进行客观部分的求解,然后考虑主观因素确定整体属性权重。 2.3.1 基于得分函数客观权值的确定 对于实际应用中的多属性决策问题,得分函数通常被认为是描述概率犹豫模糊集中信息特征的有效工具。然而,当两个概率犹豫模糊集的分数值相同时,则需要区分它们。为了克服这一缺点,扎瓦德斯卡斯[13]提出了一个基于平均值和犹豫度的犹豫模糊语言元素的得分函数,它可以完全反映概率犹豫模糊集的分散度和特征,而不必在决策过程中分离绑定的值。其公式为: (11) 考虑到概率犹豫模糊环境下多属性决策情况的复杂性,基于得分函数,进一步得出客观属性决策模型如下: (12) j=1,2,…n 2.3.2 基于最小相对熵原理的总权重确定模型 实际上,DM通常在属性值及其重要性上有所不同,而且每个DM的权重都会取决于个人判断而有所不同。因此,综合所有决策者对属性权重和客观的决策信息的评价是很重要的。采用一种基于最小相对熵原理的合适而有效的方法进行了主观和客观属性的权值进行结合。该方法不仅考虑了所有决策者的意见,还考虑了决策者权重和客观的决策信息。其应用公式如下: (13) j=1,2,…,n 针对在属性权重、专家权重都未知的情况下,利用群体一致性调节法和基于最小相对熵原理的主客观相结合法对决策者、属性权重进行求解之后,提出了一种基于前景理论和VIKOR法进行结合的排序方式,来解决多属性群决策问题,利用以下步骤构建整体算法模型: 步骤3依旧前景理论思想,对于决策者收益损失决策矩阵D(dij)=[dij]m×n,其对应的前景决策矩阵V(vij)=[vij]m×n, (14) i=1,2,…,m,j=1,2,…,n 步骤4基于VIKOR方法思想,对前景决策矩阵进行正、负理想解的确定。正、负向理想前景值如下: (15) i=1,2…,m (16) i=1,2…,m 步骤5计算各个决策方案属性上群体效应测度、个体后悔测度。 收益型属性上的概率犹豫模糊群体效应测度、个体后悔效应测度以及妥协测度由以下公式得到: (17) (18) 步骤6利用式(19)计算得到的各个方案的妥协测度Qi对所有方案排序,μ为代表的是属性的整体效用最大化方法权重,μ越大,表明群体效应中决策者偏好中所占比重越大。一般情况取μ=0.5。Qi的值越小代表该方案越优。 (19) 为了更好地建设实验室综合水平,某航海类高校领导小组经开会讨论,最终组织了实验室保卫部门D1、技术部门D2以及管理部门D3的相关负责专家对其校内的船机修造工程实验室A1、航海工程与训练实验室A2、航海动态仿真实验室A3、物流与交通运输实验室A4、轮机模拟实验室A5以及求助与打捞实验室A6等6个实验室进行打分评估。对实验室的评价研究最重要的就是评价属性的确定,也是进行实验室评价的首要步骤,简洁合理的属性直接影响着决策结果的真实性以及合理性。因此,在确定属性的过程中一定要遵循指标选取的科学性、系统性、适用性以及可比性的原则。通过查阅文献[14-16]和专家访谈等方式以及参考航海类高校人才培养方案,总结归纳近几年高校实验室评估工作经验,最终概括得到环境安全C1、仪器设备C2、师资保障C3以及实验教学C4这4个航海类高校实验室评价属性并依此对实验室进行评估。并且这3组专家针对这6个实验室的4个属性给出了概率犹豫模糊决策矩阵M1~M3如表1~3所示。根据经验给出的专家初始权重分别为0.3、0.3和0.4,给出的主管属性权重均为0.2以及专家给出的主观期望矩阵。 表1 专家D1初始评价矩阵 表2 专家D2初始评价矩阵 表3 专家D3初始评价矩阵 ω=(0.220 0,0.313 5,0.183 0,0.284 0)T 表4 整体加权评价矩阵 步骤3基于前景理论思想,根据式(4)~(6)得到收益损失矩阵D(dij)=[dij]m×n,并依据式(15)得到前景值矩阵如下所示: 步骤4根据式(16)~(17)确定正、负理想解为 V+={0.203 0 0.928 9 -0.590 0 0.471 4} V-={-0.578 7 -0.695 5 -1.058 3 -0.780 5} 步骤5根据式(17)~(18)得到各个实验室评价属性上的群体效应测度、个体后悔测度: S1=0.244 9,S2=0.128 2,S3=0.300 3 S4=0.420 5,S5=0.155 0,S6=0.140 0 R1=0.161 1,R2=0.071 7,R3=0.181 4 R4=0.182 6,R5=0.152 0,R6=0.084 5 步骤6根据式(19)得到各个实验室的妥协测度以及排序结果: Q1=0.602 9,Q2=0.000 0,Q3=0.789 4 Q4=1.000 0,Q5=0.407 9,Q6=0.077 6 为了使决策结果更加直观展现出各个实验室的优劣程度,将实验室评价属性上的群体效应测度、个体后悔测度以及妥协测度用折线图表示出来,从图1中很容易看出该航海类高校的6个实验室的排序结果为:Q2≻Q6≻Q5≻Q1≻Q3≻Q4。 图1 实验室群体效用、个人后悔测度以及妥协测度对比 由上述内容可知,6个实验室的排名结果为航海工程与训练实验室最优,其次是求助与打捞实验室,排名最后的为物流与交通运输实验室。为了进一步分析各个实验室的评分水平存在的差异,更好地解决实验室建设过程中的优势与不足,继续分析模型求解过程得出以下结果。 3.2.1 主客观权重赋权法对比 根据图2可以看出,主观赋权值一样,不能体现出各个属性之间的差异,进而导致评价结果意义不大或者与现实相悖;而客观赋权法得到的权值波动幅度较大,并且它仅仅依赖数据本身的离散程度,没有考虑到专家的主观偏好,因此客观性太强;如此看来,采用主客观结合的综合赋权法,既考虑了属性之间重要程度的差异性,又结合了数据本身的特点以及专家的经验偏好。因此,该校实验室评估过程中的属性赋权方法合理有效,并且由此得出实验室建设最重要的就是实验教学,这与现实情况相符。 图2 主科观权重赋权法对比图 3.2.2 从属性得分方面分析评估结果 根据图3可以看出,A2实验室仪器设备方面尤为突出,只是在占比较小的师资保障和环境安全方面略低,但完全不影响其整体建设水平,因为其过硬的仪器设备未来一定会带动实验教学成果,因此其获得综合排名第一,说明未来最具发展前景;A6实验室各个属性均衡发展,但是各方面都还有上升空间;A5实验室其他方面水平都还不错,但是在师资保障方面是最差的,这也就是其排名只能在中间的原因;A4实验室之所以排名最后,经分析该实验室在其他方面不突出的情况下,实验教学方面最差,因为该校专家认为实验室建设首要还是教学水平,如果不注重实验教学实力的发展,那么一定会影响未来实验室整体建设水平。 图3 各实验室属性前景值值对比图 本文针对航海类高校的办学特点以及人才培养模式,在复杂的决策环境下,应用概率犹豫模糊语言,将决策者的犹豫心理以概率语言的形式量化;并且基于前景理论思想,充分将决策者置于主客观相结合的决策环境中,是决策更接近现实;在专家属性未知、评价属性未知的条件下,充分利用群体一致性原则和最小相对熵原理对其进行赋权处理,最后应用前景理论思想和VIKOR法组合构造出一个合理可行的航海类高校实验室评估模型。本文在决策者数量方面较少,未来的研究可以将目标放在决策数量或者决策者人群方面,比如将学生的意见也考虑其中;此外排序方式方面还可以基于后悔理论或者结合各类聚合算子对备选方案进行排序择优。
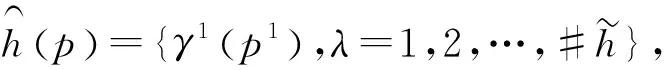
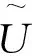
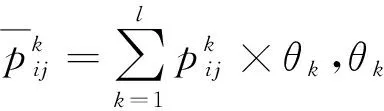
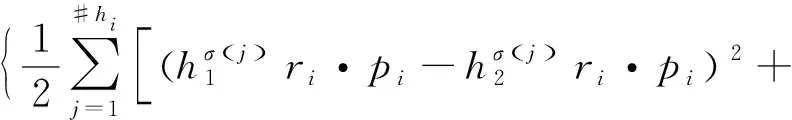
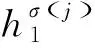
1.2 前景理论
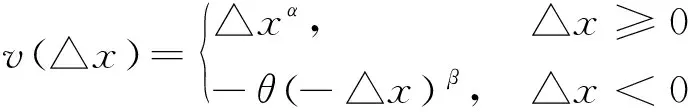
2 概率犹豫模糊环境下多属性决策评价模型
2.1 概率犹豫模糊语言多属性群决策问题描述
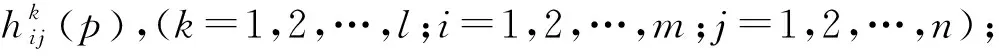
2.2 基于群体一致性原则的专家权重调节

2.3 整体属性权重确定模型

2.4 基于前景理论的VIKR法综合评价模型
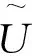
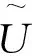

3 实例研究
3.1 实例模型求解

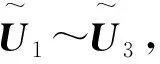
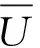

3.2 模型结果分析
4 结 语

