泾河流域水沙联合分布特征分析及其不确定性评估

邵 佳

（安徽省交通航务工程有限公司，安徽 合肥 235200）

泾河是黄河二级支流，始于宁夏泾源六盘山，流域总面积为45 421 km2，是渭河最大的支流之一，占渭河流域面积的33.7%，河道全长高达455.1 km。泾河流域属于温带大陆气候，降雨总量偏少，但过于集中。据初步统计，流域在1951—2019 年之间年均降水量约为517.9 mm，多集中在7～9 月之间，泾河流域年均流量为16.25 亿m3，集水面积约为43 216 km2。

1 泾河流域水沙联合分布特征分析

泾河流域的张家山水文站上游河段，作为黄河水沙联合典型流域，流经黄土高原，具有河段比降明显、河床冲刷严重、流速快、四周植被覆盖率低等特点。参照张家山水文站监测数据，获取张家山上游泾河流域近一年径流量及输沙量，分析其变化过程。考虑该流域汛期径流量占比大，且输沙量多的问题，研究择取汛期径流量与输沙量之和（6～10 月），作为水沙联合分布模型数据依据，流域水系如图1 所示。

图1 泾河流域水系图

1.1 水沙联合分布模型搭建

广义极值分布、对数正态分布、P-Ⅲ分布、Gamma分布是水文分析中的常用概率分布类型。用上述4 种分布拟合张家山水文站径流量与输沙量边缘分布，以AIC准则选择最优的边缘分布；基于Copula 函数建立水沙联合分布模型，以AIC 准则选择最优的联合分布。基于此，计算径流量与输沙量的联合“或”重现期下的“最大可能组合”联合设计值，应用蒙特卡洛方法评估样本不确定性对水沙联合设计值的影响，利用二维自适应核密度估计方法计算该联合设计值的置信区间；为进一步分析该联合设计值的不确定性随重现期变化的关系，采用联合熵量化不同重现期下该联合设计值的不确定性。四种边缘分布概率密度函数如下式：

式中：Γ（α）表示α 的伽玛函数；α 为形状参数；β 为尺度参数；x0表示分布函数的位置未知参数。

式中：α 为形状参数；β 为尺度参数；ξ 表示分布函数的位置参数。

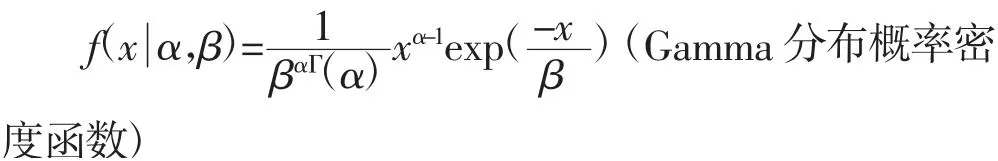
式中：α 为形状参数，β 称为尺度参数。

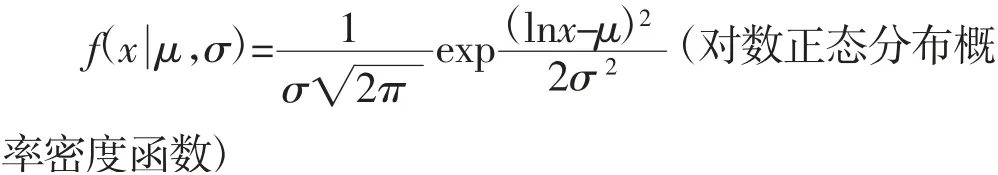
式中：μ 为函数的平均值；σ 为函数的标准差。

为便于研究，将X和Y设定为该流域年径流量和年输沙量，设计为x和y。参照上述四个密度函数，边缘分布值假设为Fx（x）和Fy（y）。根据条件分布定理，X和Y联合分布函数可用平面Copula 函数C指代。由此可列出算式：

F（x，y）=Cθ（θ 为Copula 函数的参数）（Fx（x），Fy（y））

1.2 水沙联合变量重现期判断

重现期是水工领域的概念，是评估流域量级的重要指标。学术界将重现期分为“或”“且”和二次重现三种。限于篇幅，本文着重研究“或”重现期。

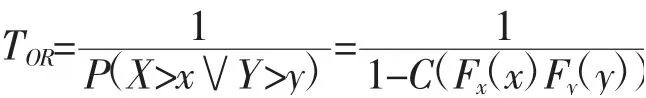
1.3 水沙联合变量设计

当给定重现期T时，临界概率水平为p，求得值为唯一解，此方式被广泛应用水工建设。针对两种变量，求解相对复杂。当给定水沙联合TOR时，理论上包含数种流量和沙量组合方式，并且满足二维坐标标准，可用等值线描述。水沙联合等值线所有点位均可代表一种组合方式，并且取相同的TOR值。但是，为让研究数据贴近实际，需找寻一组最大可能组合，即联合概率密度函数取值最大时的设计值。

1.4 结果评估

为测定张家山水文站上游泾河流域水沙联合序列之间的关系，上文采用Kendall 秩的相关检验法，将水文站监测数据输入水沙联合分布模型，得出P值约为8.003×10-9。P值远小于0.05，因此原假设不成立，初步认为该流域水沙联合分布特征，在二维序列上具有显著的相关性，有必要研究泾河流域水沙耦合关系，全面分析径流量和泥沙量的内在关联，健全水沙分布模型。

应用上文四个密度函数测试流域边缘分布参数值，径流量分布密度函数及概率密度函数见图2。

图2 径流量分布密度函数及概率密度函数

输沙量分布密度函数及概率密度函数见图3。

图3 输沙量分布密度函数及概率密度函数

参照上图，采用K-S 检验法对水沙联合边缘分布特征进行假设，择取最优边缘分布数据。结果表明，该流域从预设的四种水沙联合分布特征中的P值均大于0.05，与原假设设定相符，初步认为该结论验证原假设，意味着径流量和输沙量最优拟合状态均属于正态分布趋势。

2 泾河流域水沙联合分布计算不确定性评估

2.1 评估流程

本研究采用蒙特卡洛统计理论，分析分布特征计算的不确定性。抽调多例样本，采用重复抽样法，判断不确定性对水沙联合设计的影响。具体流程为：基于Copula函数联合分布模型总体架构，调取二维样本，用蒙特卡洛统计法随机模拟1 000 次；应用观测值的水沙联合分布模型相同估算参数方法，模拟样本联合分布模型，得到1 000 组数据，评估置信水平下的估计区间；所有数据中，以20 a 为重现期起始点，按照10 a 一梯度上升到100 a，判断最大可能组合的水沙联合设计值。

2.2 水沙联合信息熵的不确定分析

信息熵可描述随机变量的分散程度，是信息最为基本的组成单位。常规条件下，信息熵可针对一维数据，也可应对多维情况，将测的数据定义为联合信息熵。由于信息熵可作为判断变量的重要依据，可认为信息熵越大随机变量的分散程度越大，也就是不确定性越明显。

2.3 结果评估

测验过程中，需解决识别问题。从本质上讲，不确定性理论发展迭代了传统优参识别系统。为寻得最有可靠模型参数，不确定思想在统计学基础上可通过大量参数分布获取更具现实意义的结论。采用蒙特卡洛统计法研究不确定性，获取模型参数置信水平下的参考范围，为理解水沙联合模型提供了技术支撑。

根据表1，张家山站水沙联合分布模型存在明显的不确定性，联合分布参数变幅高达55.64%。据此绘制“或”重现期等值线图（见图4），根据图中克制，泾河流域水沙联合分布模型给出不同程度径流量和输沙量遭遇组合的重现期。工程中多选用“或”重现期作为风险控制参量，或安全评价标准。通过计算泥沙频率和洪水频率组合，确定流域不同时段的最大或最小淤积量。水沙联合重现期与设计值是否准确决定着流域工程是否经济、安全且科学，既关乎周边生态，还关乎工程社会效益。设计过程中需合理评估设计标准，降低误差值，求解最优解，为工程合理建设提供参考。

表1 水沙联合分布模型参数估计区间

图4 等值线图

针对信息熵，可将其作为评价不确定性的指标，信息熵与不确定呈正相关关系。张家山站联合设计值存在明显的不确定性，在重现期影响下，联合熵呈现明显增加的趋势（需要重现表述），意味着联合设计值具有显著的不可控性。

3 结语

考虑到泾河流域水土流失严重的问题，建立了水沙联合分布模型，对水沙组合潜在风险进行评估，从中寻求最优解。随后基于蒙特卡洛方法对分布模型的不确定性进行评估，计算百年内重现期的最大可能组合下的最优设计值，并分析其信息熵。结果表明，泾河流域水沙联合分布模型及水沙联合设计值存在高度不确定性（需要重现表述），意味着泾河流域设计值面临巨大挑战，在重现期年限增长的同时，设计值不确定性将进一步提升，将对水工建设提出更高的要求。