初中数学命题缺陷分析模型的构建及缺陷规避对策

325600 浙江省乐清市乐成第一中学 陈江嵩

近年来，国家层面对有关命题工作的关注有了新变化，各级教育部门对命题工作越来越重视，涉及命题工作的各级研修越来越多

.

2019年6月23日，《中共中央 国务院关于深化教育教学改革全面提高义务教育质量的意见》提到“稳步推进初中学业水平考试省级统一命题，坚持以课程标准为命题依据，不得制定考试大纲，不断提高命题水平”

.

2019年11月22日，教育部专门为中考命题工作下发《教育部关于加强初中学业水平考试命题工作的意见》，文件指出“考试命题对学校教育教学具有重要引导作用，是健全立德树人落实机制、扭转不科学教育评价导向的关键环节”，由此可见，国家越来越重视命题及其产生的导向作用

.

同时，做好命题工作也是精准教学的精准点，研究命题的常见缺陷是提高教师命题技能的精准点，也是精准教学深层次的挖掘点

.

一、 相关研究阐述

大部分研究者认为提高命题技能水平需要教师掌握或理解各种技能，有很多书刊介绍各种命题技能，供教师学习，如原浙江省初中教研员许芬英等编著的《数学命题技术研究》，潘小梅所著《初中数学教学研究入门36问》中有一章节提出命制各类数学问题的策略等

.

也有部分研究者另辟一路，研究命题缺陷，主要针对命题缺陷进行分类并作简单分析，对教师进行纠错教育，就像教师在学生犯错时让学生从错误中得到感悟，如李春雷的《数学命题常见错误例析》，王琪的《数学命题中常见的错误及其诱因分析》等

.

综观有关命题缺陷研究的文献资料，它们重分类而轻分析，有待深入，较少涉及规避命题缺陷的对策，尤其缺少可操作的命题缺陷分析模型；文献资料中用“命题错误”来描述命题缺陷是有待商榷的

.

这些发现为笔者的研究提供了契机

.

二、 构建命题缺陷分析模型的过程

在查阅文献与命题研究分析的基础上，笔者认为，根据产生命题常见缺陷的诱因和思维层次，可以将出现的各种命题缺陷分为知识性、逻辑性、心理性三大类，由此形成分类框架(如图1所示)

.

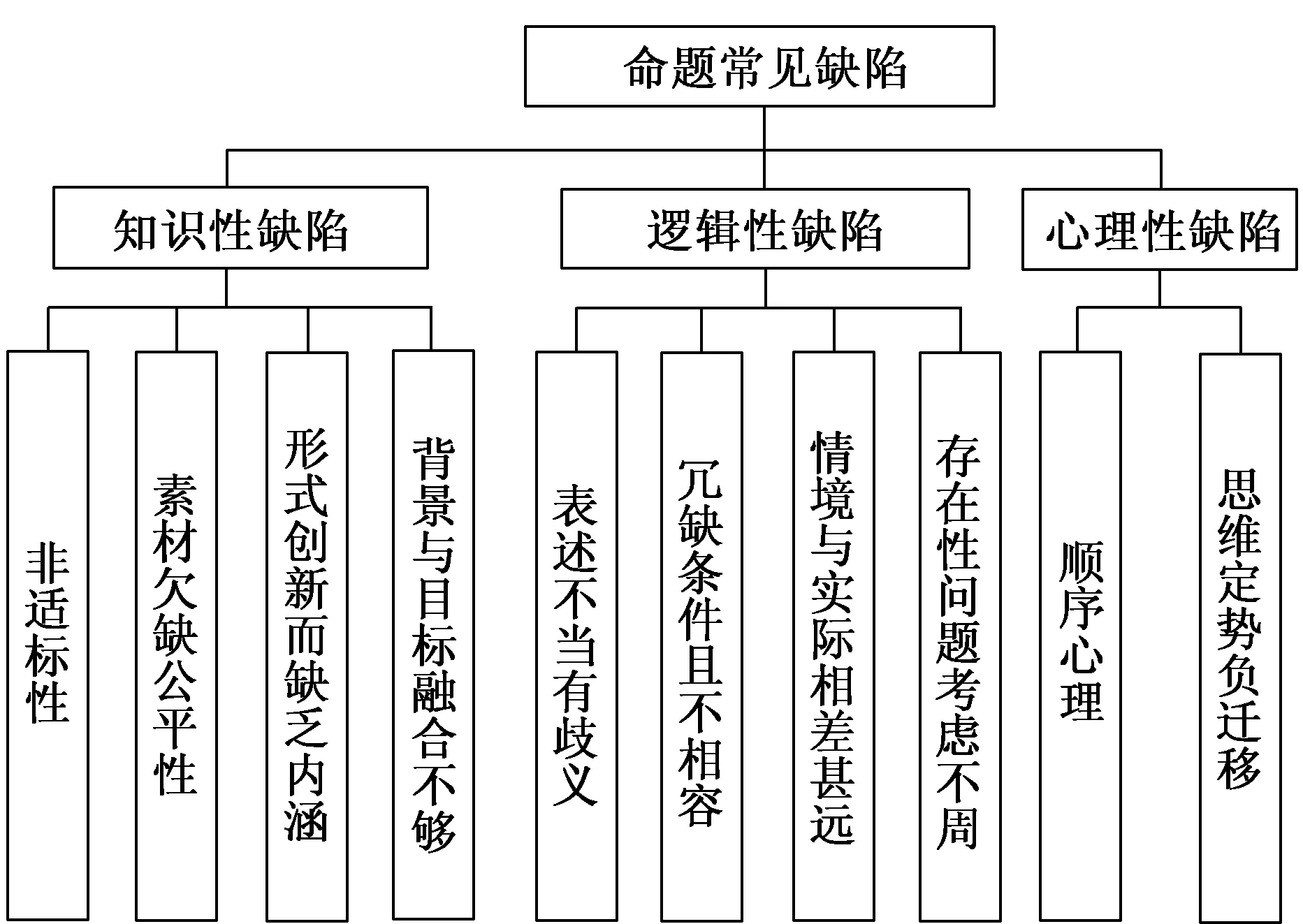
图1

考虑到进行命题分析的试题不局限于中考试题，对于“形式创新而缺乏内涵”的界定，笔者认为其界线模糊而难以定性，对于知识性缺陷中的“非适标性”“素材欠缺公平性”“形式创新而缺乏内涵”在模型中也不予设项

.

此外，对于心理性缺陷中的“顺应心理”与“思维定势负迁移”，这两个角度过于接近，笔者考虑将其归于一类：思维定势负迁移

.

笔者通过教学实践的检验，鉴定存在命题缺陷的各类试卷，并进行汇总，其中包括近几年某县市各校各年级的期末模拟试题、温州市各县市各年级的期末试题、近几年各地部分高中自主招生试题及模拟试题，共56份试卷

.

笔者将命题缺陷以上述方案进行统计分类，再对统计的结果进行数据分析(如图2所示)

.

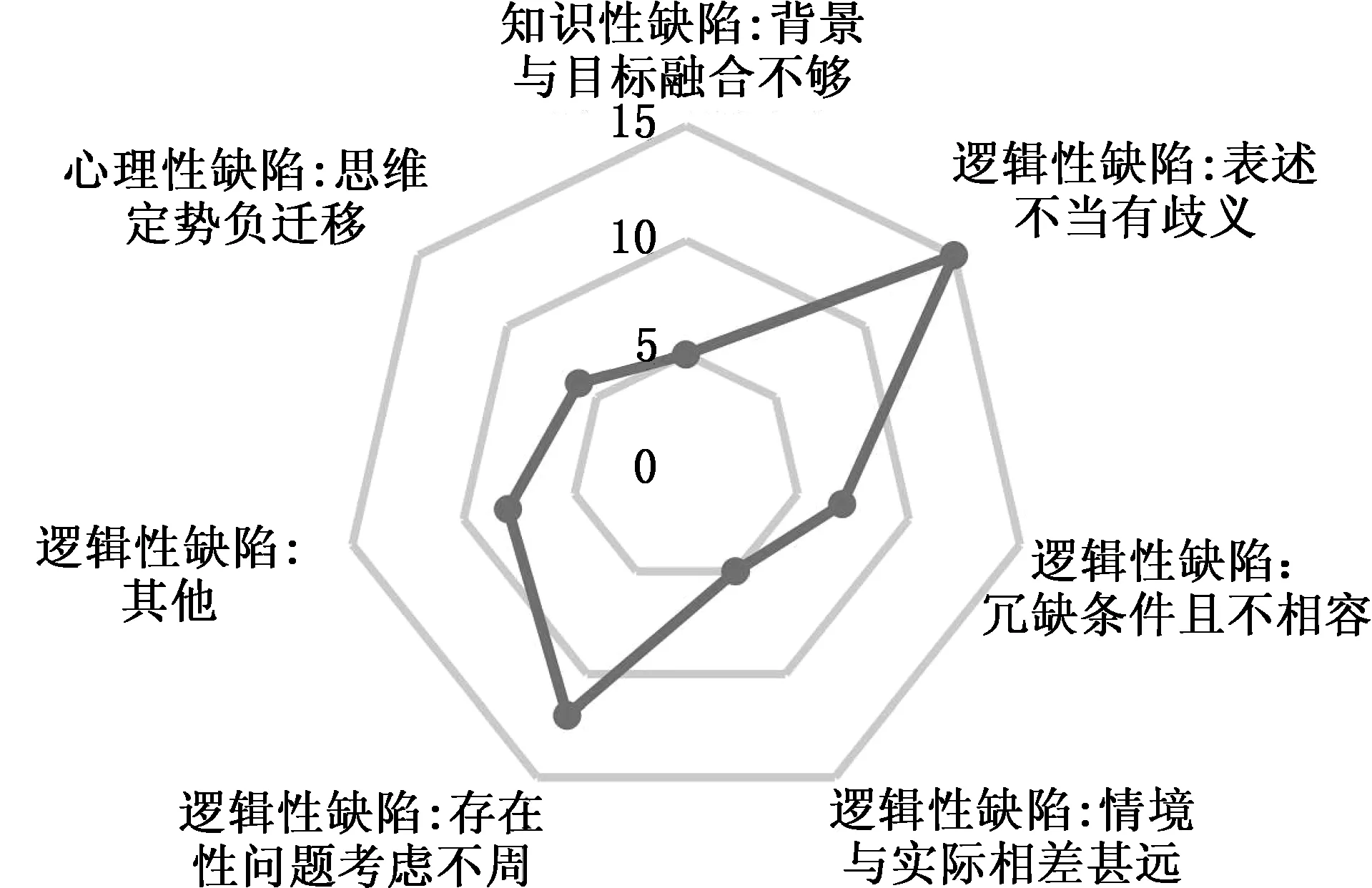
图2

以上分类反映了常见命题缺陷

.

当然，对于诸如“选项设置犯错”“以偏概全”“概念不清”等命题缺陷的归类问题，考虑类别设置太多、太杂会不利于研究问题，需要对类别进行精简

.

英国数学家Bertrand Arthur William Russell认为数学推理依靠逻辑，数学为其证明所具有的逻辑性而骄傲，“数学，作为人类思维的表达形式，反映了人们积极进取的意志，缜密周详的推理以及对完美境界的追求”

.

逻辑是数学的基本要素之一，数学问题出现缺陷时总会出现逻辑问题，因此，知识性与心理性命题缺陷都可以归入逻辑性命题缺陷，只是思维层次有所不同

.

同样的，笔者将“选项设置犯错”归于条件冗缺类，“以偏概全”归于存在性问题类，“考虑不周”“概念不清”归于表述不当有歧义类

.

笔者还添设其他逻辑性缺陷这一类，将有关命题者心理作用引起的设计缺陷、“思维定势负迁移”归于此类

.

于是，笔者重新设计了常见命题缺陷的分类框架(如图3所示)

.

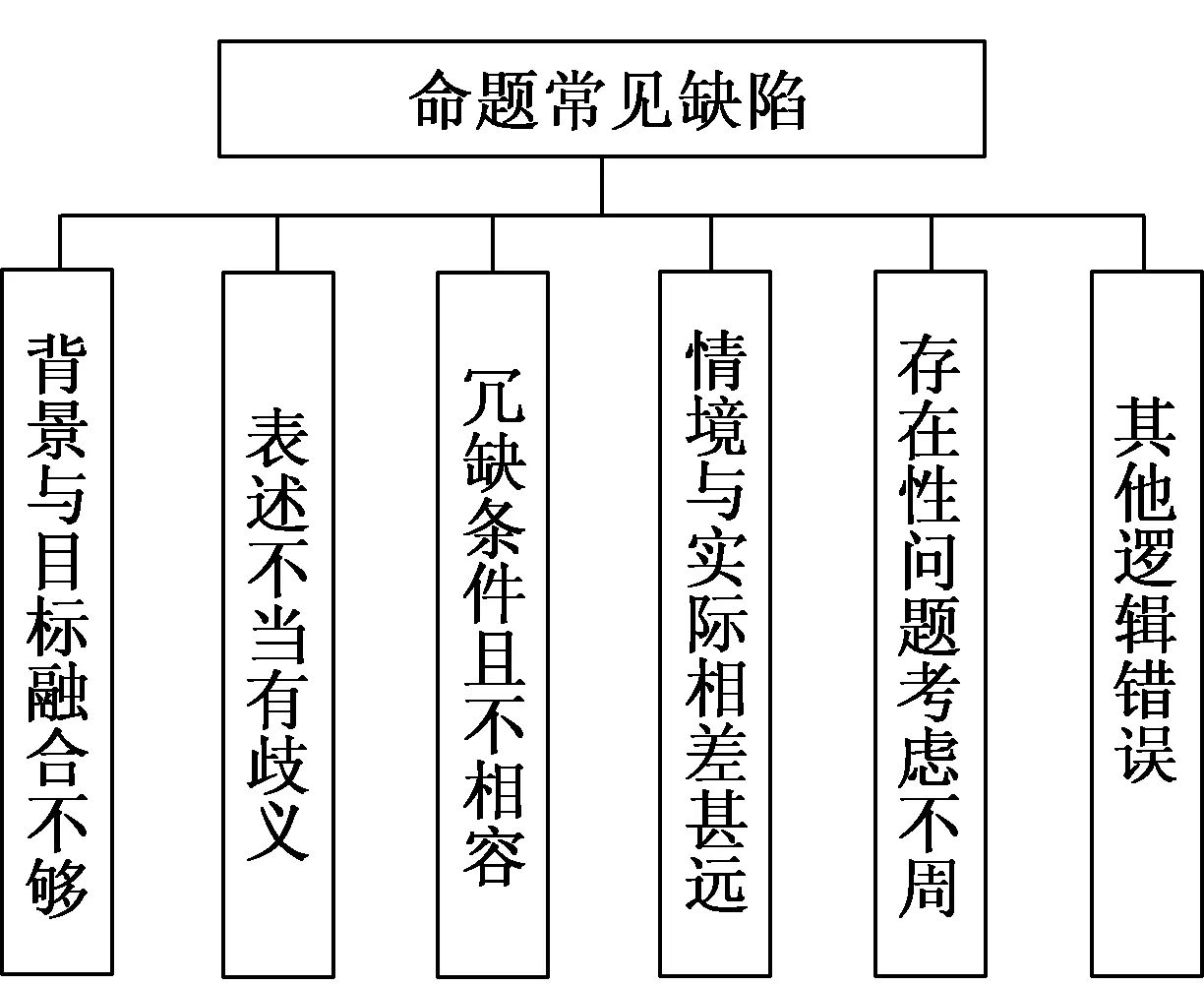
图3

命题常见缺陷分类确定后，笔者基于体现科学性原则、重视符合实际原则、形成良好导向原则等考虑，从背景与目标融合度、表述明晰度、条件精简度、情境与实际相符度、存在性周全度、其他逻辑严密度这六个维度鉴定命题缺陷

.

参考《华人如何学习数学》一书中关于数学课程的综合难度模型(如图4所示)的构建过程，形成命题常见缺陷分析模型(如图5所示)

.

图4

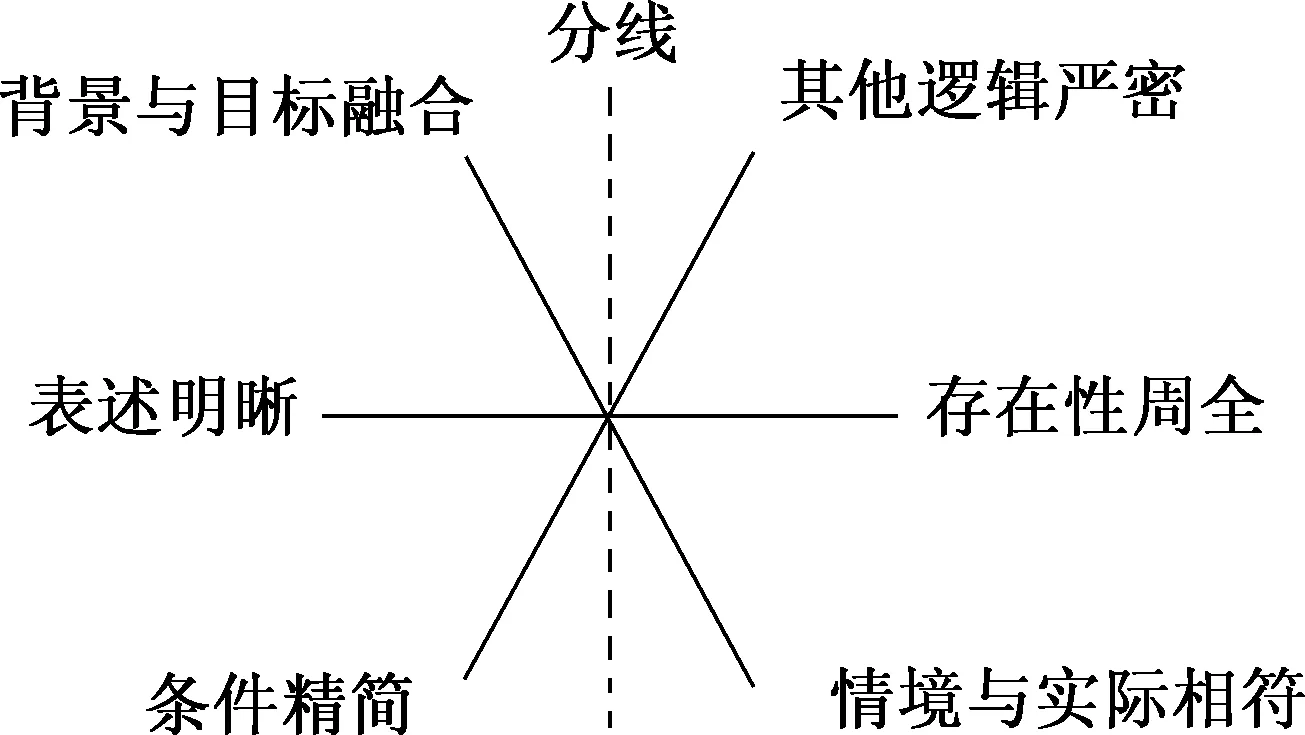
图5

其中，背景与目标融合度属于知识技能层面逻辑性，表述明晰度、条件精简度、情境与实际相符度和存在性周全度属于数理层面逻辑性，其他逻辑严密度主要考虑的是命题者因心理层面问题引起的逻辑性错误

.

因此，从层次上看，从背景与目标融合度到其他逻辑严密度呈逆时针方向逐步提升

.

讨论命制问题是否存在缺陷，中间分线左侧各个维度(即背景、表述和条件)是首先要考虑的，然后再考虑分线右侧的各个维度(即实际、存在性、其他逻辑)

.

基于以上分析，通过表1进行直观说明

.

表1 命题常见缺陷分析维度划分

命题缺陷维度从低到高所属层次考虑顺序所属逻辑性缺陷层面背景与目标融合表述明晰条件精简一二三首先考虑背景、表述和条件知识性层面数理层面数理层面情境与实际相符存在性周全其他逻辑严密四五六再考虑实际、存在性、其他逻辑数理层面数理层面其他逻辑层面

为了使模型具有可操作性，笔者制作了《命题常见缺陷指数分析表》(如表2所示)，成立命题审卷分析小组，对审查题目进行分析打分，一颗星为2分，五颗星为优

.

确定指数分析表中最后数据的方法为求小组成员打分的平均分，再参考进一法，最后集体商议获得最终结果

.

表2

分析维度水平星级指数(★★★★★) 思前①背景与目标融合②表述明晰③条件精简想后④情境与实际相符⑤存在性周全⑥其他逻辑严密说明:★或★★为差;★★★为中;★★★★为良;★★★★★为优

三、 案例：存在性周全度不足与表述明晰度不高的命题缺陷分析

案例一

1

.

问题来源：某地中考适应性试题如图6-1，在Rt△

ABC

中，∠

ACB

=90°，

AB

=5，过点

B

作

BD

⊥

AB

，点

C

,

D

都在

AB

上方，

AD

交△

BCD

的外接圆⊙

O

于点

E.

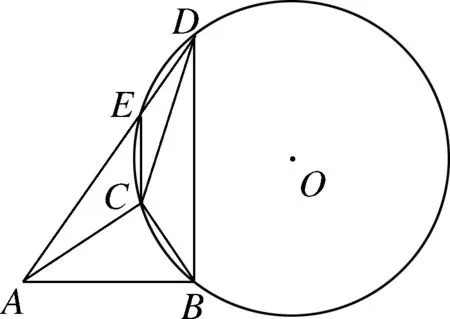
图6-1

(1)求证：∠

CAB

=∠

AEC.

(2)若

BC

=3

.

①

EC

∥

BD

，求

AE

的长

.

②若△

BDC

为直角三角形，求所有满足条件

BD

的长

.

(3)若则________

.

(直接写出结果即可)2

.

命题缺陷指数分析此案例的命题缺陷指数分析如表3所示

.

表3

分析维度水平星级指数(★★★★★) 思前①背景与目标融合★★★★②表述明晰★★③条件精简★★★想后④情境与实际相符★★★★⑤存在性周全★⑥其他逻辑严密★★说明:★或★★为差;★★★为中;★★★★为良;★★★★★为优

图6-2图6-3

3

.

命题缺陷评析题目的小问(1)为证明题，命题者意在设置如图6-1所示的点

C

和点

E

的位置，让学生根据圆内接四边形对角互补、平角互补，再结合已知条件推得结论∠

CAB

=∠

AEC.

但此处对条件的设置考虑不周，存在多种情况，例如当点

C

在点

E

上方时，易证得∠

CAB

+∠

AEC

=180°，而并非相等(如图6-2所示)；当点

D

与点

E

重合时，∠

CAB

与∠

AEC

就没有什么数量关系了(如图6-3所示)

.

笔者认真分析后认为，这个疏漏问题的源头是命题者在构思问题、设置条件时认为∠

BCD

为钝角，则点

E

始终在点

C

的上方，形成了思维定势，忽略了图形相对位置的不确定性，而此处本需要分类讨论

.

因此，针对小问(1)理应增设一个条件“当点

E

在点

C

的上方时”

.

根据点

E

与点

C

相对位置的不确定，小问(3)的求解自然也需要分两种情况：当点

E

在点

C

上方或当点

E

在点

C

下方

.

通过作

CM

⊥

AD

，

CN

⊥

BD

，垂足分别为点

M

，

N

，易证△

CME

≌△

CNB

，通过运用勾股定理和方程思想求得

BD

，进而得面积比(如图6-4、图6-5所示)

.

图6-4图6-5

案例二

1

.

问题来源：某地中考适应性试题

某单位计划购进A，B，C三种型号的礼品共2700件，其中C型号礼品500件，A型号礼品比B型号礼品多200件．三种型号礼品的单价如表4所示.

表4

型号ABC单价(元/件)302010

(1)求计划购进A和B两种型号礼品分别多少件.

(2)实际购买时，厂家给予打折优惠销售(如打8折指原价×0.8)，在计划总价额不变的情况下，准备购进这批礼品．

①若只购进B，C两种型号礼品，且B型号礼品件数不超过C型号礼品的2倍，求B型号礼品最多购进多少件.

②若只购进A，B两种型号礼品，它们的单价分别打

a

折、

b

折，

a

<

b

<10，

a

，

b

均为整数，且购进的礼品总数比计划多300件，求

a

，

b

的值．2

.

命题缺陷指数分析此案例的命题缺陷指数分析如表5所示

.

表5

分析维度水平星级指数(★★★★★) 思前①背景与目标融合★★★★②表述明晰★★③条件精简★★★想后④情境与实际相符★★★★⑤存在性周全★★★⑥其他逻辑严密★★★说明:★或★★为差;★★★为中;★★★★为良;★★★★★为优

3

.

命题缺陷评析此题目中小问(2)的①表述不当，会产生歧义，命题者原意是小问(1)的情况下厂家没有给予打折优惠销售，但在小问(2)的题干中明确提出“实际购买时，厂家给予打折优惠销售”，于是误导部分学生认为小问(2)的①条件中应该有打折，但又发现题中没有明确哪种型号打折和打几折

.

命题者在题干中为了让学生理解打折的意思添加了解释“如打8折指原价×0

.

8”，被一部分学生误认为是打8折，于是产生了多种情况的理解：B、C型礼品都打8折；B型礼品打8折，C型不打折；C型礼品打8折，B型不打折.这些困惑会造成学生的多解、计算困难等问题，对此题的评价起了消极作用.

四、 命题缺陷的规避对策

(一)背景与目标融合度不够

从知识与技能层面思考命题考查目标，可以将背景与目标融合度具体细分为背景与知识目标融合度以及背景与方法技能目标融合度

.

这类命制缺陷，主要通过调整双向细目表制作内容和设定制作时间两方面进行规避

.

1

.

双向细目表中增设背景与考查目标栏目，认真核对考查目标与背景内容契合度，适当删增背景材料使其与考查目标一致

.

2

.

双向细目表设在命制试题前、命制试题后两次制作，进行前后比对，若发现有问题，根据考查目标改变问题方向，让背景与目标尽量融合

.

(二)表述明晰度不高

命题中的条件表述不明确会给解题者造成逻辑混乱的困扰，造成歧义，影响本题甚至整张试卷的评价效度和信度

.

数学命题组完成数学题目初稿后，可以邀请其他学科教师参与试题审查，通过学科交叉审查的方式进行评定，可能会产生更好的效果

.

职业特色带来的逻辑思维习惯可能使数学教师不易察觉表述中出现的瑕疵，而其他学科教师的参与可以减少出现这方面缺陷的可能性

.

(三)条件精简度不够

1

.

审卷人求解命制题目后，将命制题目中的条件与结论置换，再进行求解，这种正逆向解题更容易发现条件的多余与缺少

.

2

.

积极运用信息技术手段，根据已知条件构建图形查看条件冗缺

.

(四)情境与实际相符度不足

近年的中考或其他类型的选拔试题中，出现大量与生活生产紧密联系的PISA理念类试题，新颖别致，富有生活气息

.

但在这些试题的情境中，也有部分情境主观色彩过浓，与生活实际有着较大落差，缺乏真实性，对此提出一些规避对策

.

1

.

命制题目涉及实际情境数据时，要积极查询资料，在可能的情况下还需要实际测算，尤其要注意题设应满足的一些隐含条件或合理范围

.

2

.

命制题目的情境要具备合情性和可操作性，数据的编制也应具备合理性

.

(五)存在性周全度不足

1

.

“如图”与“如图所示”是命制问题绕不开的两个词，需要以慎重的态度去对待

.

图形给人一种直观感，让人容易更快理解题意，但事物总是存在两面性，有些存在性问题没有被考虑到，就是因为图形桎梏思维

.

有个别地方审查命制题目时采用无图审查法，将试题中的图形都去掉后，再让审卷人根据题意自己构建图形去解题

.

2

.

积极采用信息技术构建图形，根据题意改变图形探讨各种可能性

.

(六)其他逻辑严密度不足

出现其他逻辑严密度不足的命题缺陷，是命题者的思维定势所致

.

作为中考题能够被众多审题教师“漏过”，其原因显然不仅仅是一句考虑不周所能解释的，其中更多涉及心理因素，命题者作为个体必然存在思维的局限性，而且会相互影响

.

审查题目时如果找与命题者零沟通的组外人来进行，那么审题工作可能做得更好

.

五、 总结与反思

命题是创造行为，而创造往往需要实践检验，可能存在缺陷，需要不断改进

.

规避和改进命题缺陷可以提高教师的命题技能，提高命题技能有利于提高教师教学设计创新能力，进而提高教师的教学水平

.

命题研究的特性决定研究主体适于有一定教学研究经验的教师，而新教师由于缺乏必要的命题经验，难以深入分析

.

如何构建一种让新教师也能在命题研究中得到进步与发展的命题模式，也许是今后命题研究的一个方向

.