波浪和水流荷载作用下大直径钢圆筒贯入垂直度分析

董德龙，李伟，沈晓鹏，李书兆，吴非，李可

（1. 中海油研究总院有限责任公司，北京 100010）

（ 2. 海洋石油工程股份有限公司，天津 300452）

近年来，深插大直径钢圆筒被成功应用于港珠澳大桥，深中通道人工岛以及其他工程建设当中[1]。由于大直径钢圆筒具有地层适应广，施工速度快等优点，在港口及海洋工程中都具有较为广阔的应用前景。

针对大直径钢圆筒的设计计算，周红星（2015）结合现场试验结果，采用数值模拟的方法探讨了大直径钢圆筒的变形特性[2]；鉴于大直径钢圆筒自身的特点，针对施工的研究更为活跃。胥新伟等结合港珠澳大桥的钢圆筒施工，探讨了大直径钢圆筒振沉计算方法[3]。

现有的工程经验显示，在钢圆筒振沉过程中可能会出现偏位、倾斜现象。杨合林等（2020）指出这一现象的主要原因包括：振沉区域的环境荷载导致的圆筒位移和倾斜；地表硬层分布不均导致的筒体自沉倾斜；振沉过程中，现场操作例如吊船起重量改变，锚缆松紧度不均产生的船体变位导致的筒体偏位和倾斜[4]。由于海上安装施工风险大，作业成本高，操作程序复杂，受环境条件制约严重，为保证海上施工的顺利进行，避免振沉过程中可能的风险，有必要对环境荷载对钢圆筒垂直度影响进行分析。

海洋工程中的大尺度通常用d/L ＞ 0.2作为划分大尺度和小尺度结构标准，其中d为结构物特种尺度如柱的直径，L 为波长[5]。对于大尺度的结构物，情况就比较复杂，此时需要考虑结构自身对流场的影响[6]。目前，除了少数简单几何形式有明确的解析解，绝大多数结构形式通常需要数值计算，各种边界元方法被广泛应用[7]。对于波流作用下结构物上的荷载计算一般采用CFD软件进行计算，目前常用的CFD软件包括ANASYS Fluent，Star-CCM，OpenFOAM等等。

本文采用波浪、水流荷载和贯入过程非耦合的计算方法，对波浪，潮流在大直径钢圆筒自沉和振沉过程中垂直度的影响进行了计算分析,分析结果为现场安装操作提供依据。

1 工程背景

该工程采用直径为30m，高度15m大直径钢圆筒结构。工作海域的水深为22m, 现场的土层分布见表1。

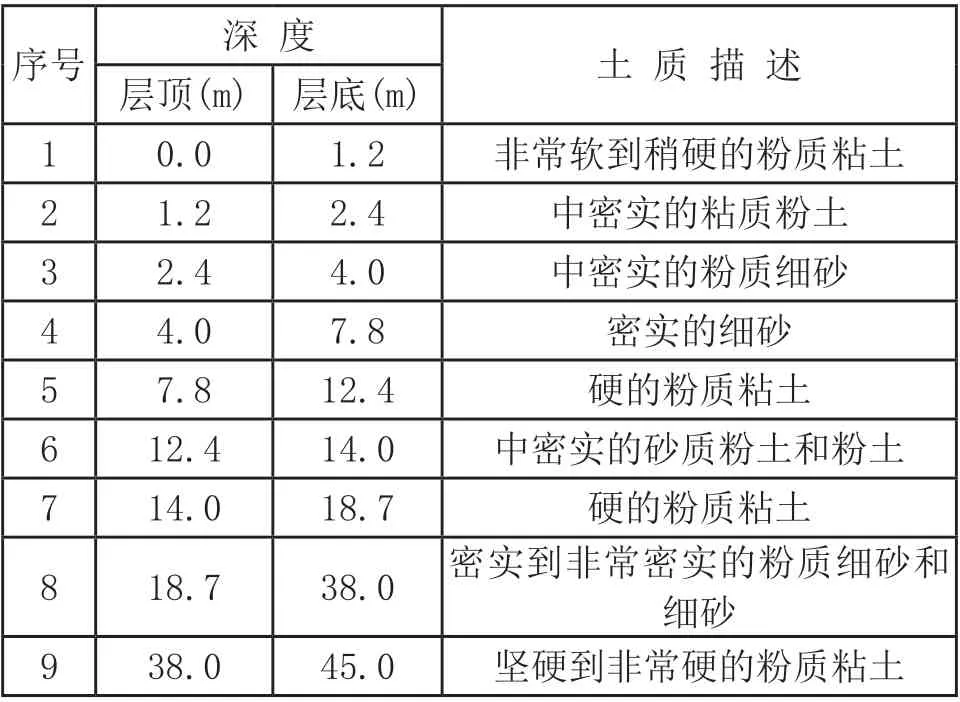
表1 现场的土层分布

在大直径钢圆筒安装时采用12台APE600液压振动锤联动进行沉桩，入泥深度15m。

由于大圆筒一直位于水面以下，因此计算中不考虑风荷载作用；对于波流采用最不利的海洋荷载。同时假设波浪传播方向与水流方向一致。在钢圆筒海上施工期间，作业的环境荷载见表2。

表2 波浪、流条件

2 数值模拟方法

本文先通过有限体积法计算作用在海底以上一定高度的大圆筒上的波浪和水流荷载，然后将计算得到的波浪和水流荷载施加在大圆筒上，通过CEL有限元法计算在该波浪和水流荷载、结构自重以及振动锤激振荷载作用下的位移情况。采用Star-CCM+软件进行有限体积法计算水动力荷载；采用Abaqus进行大圆筒的垂直度计算。

2.1 波浪、水流荷载的模拟方法

波浪传播和水流方向均取为x方向。由于对称性，计算模型在y方向上取实际模型的一半。计算域在波的传播方向长度取190m，宽度取95m，计算域的高度为27m，保证计算域的边界不影响计算结果。

计算域的左右两侧、后侧的边界条件为速度入口（Velocity Inlet），前侧的边界条件为对称面（Symmetry Plane），底部边界条件为墙（Wall），顶部的边界条件为压力出口（Pressure Outlet），大圆筒内外两侧的边界设为墙（Wall）。流体经过墙体表面时滑动速度和剪切荷载之间的关系设置为滑动（Slip）。为了避免波浪在边界出现衰减的现象，在速度入口边界激活Wave Force，Wave Force长度设置为70m。

使用多相流模型模（VOF）拟波浪荷载，使用默认的K-Epsilon 湍流模型，并在-z方向施加重力。采用5阶波浪理论，波浪特性通过选择输入周期的方式确定。

采用隐式非稳定（Implicit Unsteady）模式，时间步长为0.01s。

2.2 垂直度计算的模拟方法

采用CEL有限元分析方法进行钢圆筒垂直度的计算，其中大圆筒用Lagrange方法描述，地基采用Euler方法描述。计算的模型不考虑基槽开挖地面以上土体的影响，即认为地基底面从边坡底部开始。计算几何模型如图3所示。

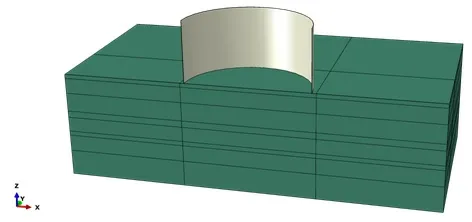
图1 几何模型

假定大圆筒为刚体，其单元类型为8节点三维体单元；地基采用Euler方法描述，为了允许大圆筒贯入过程中土体向上隆起，建立模型时在地基表面向上取0.5m为计算模型的一部分，该部分区域初始材料设置为空。

地基底部三个方向上的速度设为0，对称面上法向速度为0，三个侧面在三个方向上的速度为0。大圆筒除了在z方向位移、x方向位移和绕y轴的转动外，其他方向的位移和转动完全约束。大圆筒和地基之间设置接触面单元。切向接触面采用为摩尔剪切特性，法向接触为硬接触，允许脱离。

根据土体的类型，地基土体的力学模型采用Mohr-Coulomb理想弹塑性模型（其中内摩擦角为0的土体采用Mises理想弹塑性模型实现），根据勘察报告提供的建议值，场地土体的具体力学参数如表3所示。

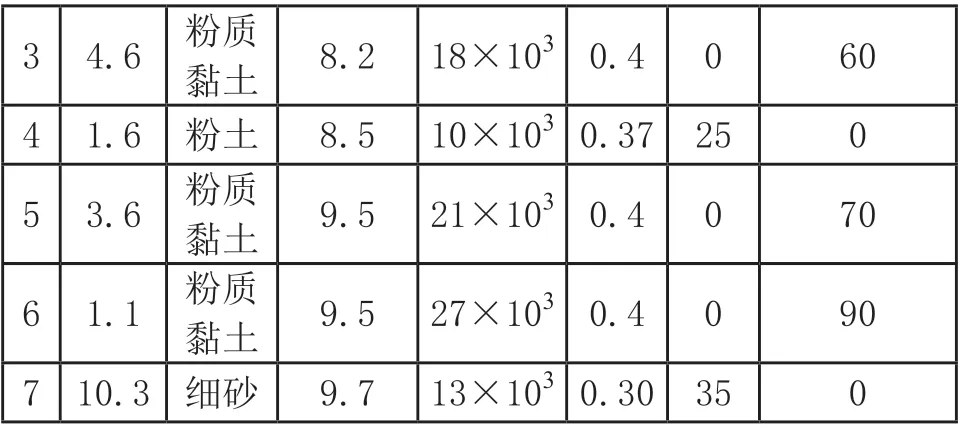
3 4.6粉质黏土8.2 18×103 0.4 0 60 4 1.6粉土8.5 10×103 0.37 25 0 5 3.6粉质黏土9.5 21×103 0.4 0 70 6 1.1粉质黏土9.5 27×103 0.4 0 90 7 10.3细砂9.7 13×103 0.30 35 0

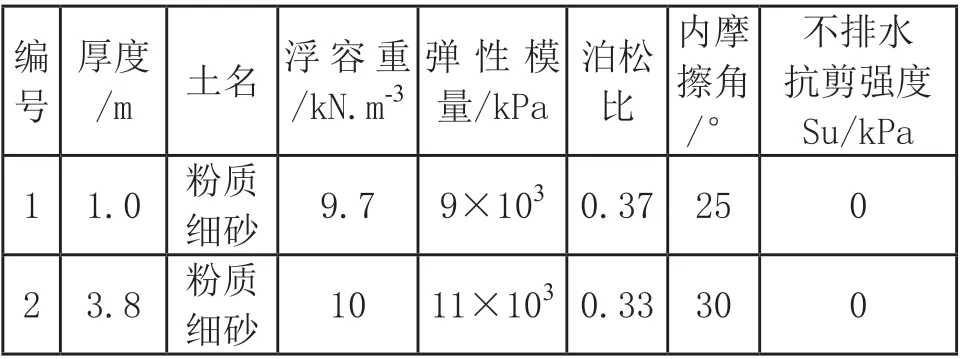
表3 海底土层性质表

在大圆筒贯入过程中，受到的荷载包括大圆筒自重、振动锤和夹具的重量、起吊辅助结构的重量、水平方向的波浪和水流荷载以及绕纵轴旋转的力矩。其中，大圆筒的重量通过在纵轴方向施加重力加速度的方法实现，振动锤和夹具的重量、起吊辅助结构的重量以集中力的形式施加在大圆筒的中心位置，波浪和水流荷载以及绕纵轴旋转的力矩的作用点位置为大圆筒在泥面高度的中心位置处。

3 计算结果及分析

3.1 波浪及水流荷载

大圆筒的存在导致水流通过该区域时水流运动状态发生改变，从图2中可以看出，由于大圆筒壁的阻挡作用，水体在大圆筒附近和内部的流动方向发生了变化。大圆筒结构物内部是空的，其内部存在流体，且该流体和外界流体联通形成一体，外界波浪和水流作用下内部水体形成一个旋涡状的流动。

图2 水流流动方向矢量图

由于大圆筒壁改变了水流的流动状态，大圆筒壁表面将受到水流对其产生的压力和粘滞力作用，从图3中可以看出，由于水流运动方向的变化，导致大圆筒壁不同位置受到的水压力不同，在筒壁阻止水流流入的位置为正水压力，而在筒壁阻止水流流离的位置出现负水压力，出现正、负水压力的具体位置与除了与筒壁的内外位置有关外，还和波浪的相位（即时间）有关。

图3 大圆筒壁受到的动水压力（单位：kPa）

将作用在大圆筒筒壁上的水压力进行积分后可以得到作用在大圆筒上的动水荷载以及水压力分布不均匀导致的力矩。从图4中可以看出，随着时间的增加，作用在大圆筒上的水平荷载和力矩也在做波动变化，而且随着时间的增加，荷载和力矩的峰值及谷值都在逐渐降低，产生这种现象的原因主要是由于隐性非稳态方法计算波浪荷载的完全传播过程需要一些时间。

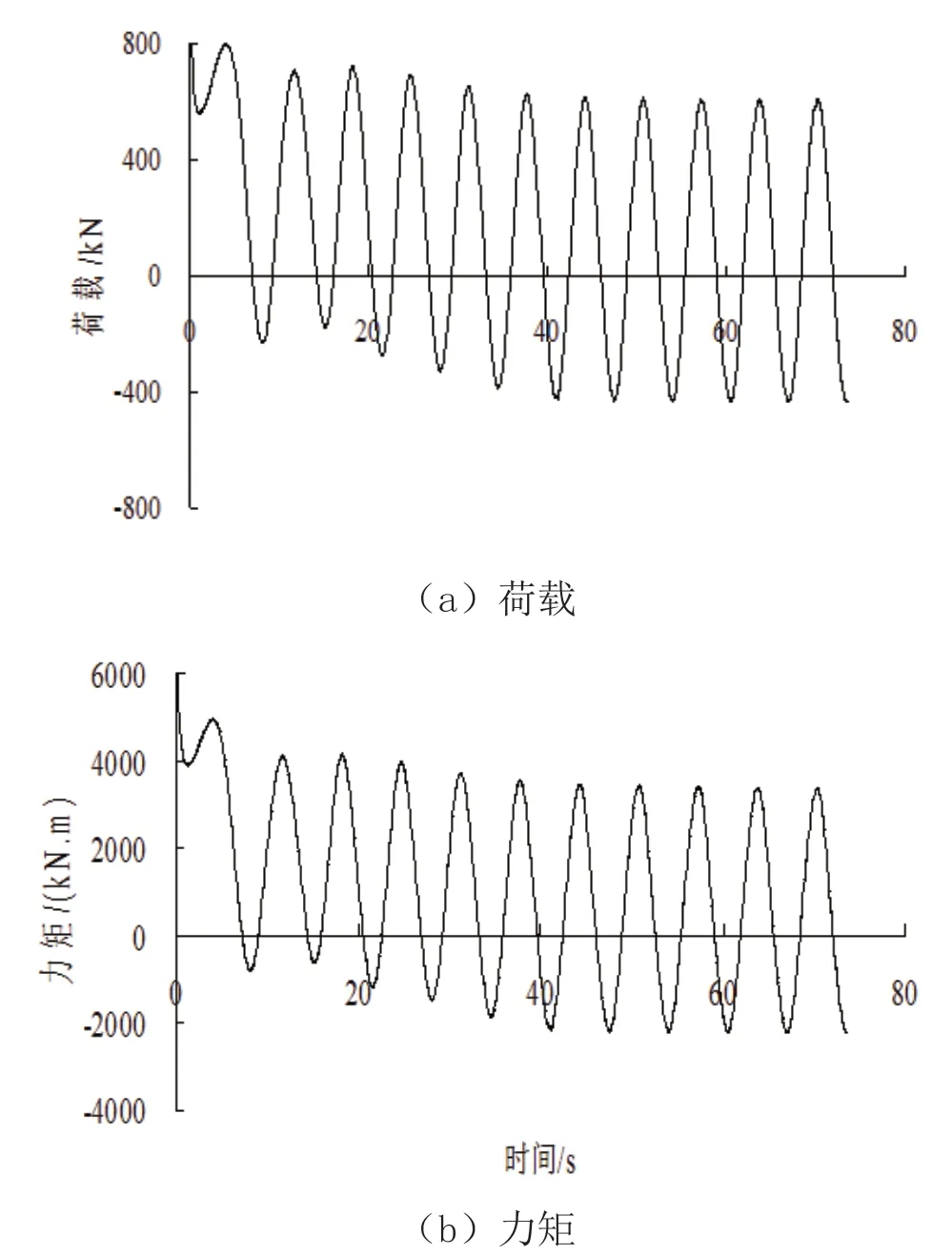
图4 作用在大圆筒上的荷载和力矩

取波浪和水流对大圆筒的荷载及弯矩变化曲线达到稳定的周期性变化时的峰值为波浪和水流联合作用下大圆筒受到的动荷载峰值，泥面以上不同的大圆筒高度对应的该峰值结果如图5所示。从图中可以看出，随着高度的降低，水平荷载和弯矩都逐渐减小，且高度越低变化幅度越小。

图5 泥面以上不同大圆筒高度对应的波浪和水流荷载

3.2 大直径钢圆筒的垂直度

计算得到大直径钢圆筒载自沉贯入过程中大圆筒的转角随底部入土深度的变化如图6所示。从图中可以看出，随着深度的增加，转角逐渐增大，当深度达到-2.99m时，沉降出现回弹，此时大圆筒的转角达到0.003，随沉降的回弹大圆筒的转角也有部分回弹，然后再次增加，最后转角达到0.0047。

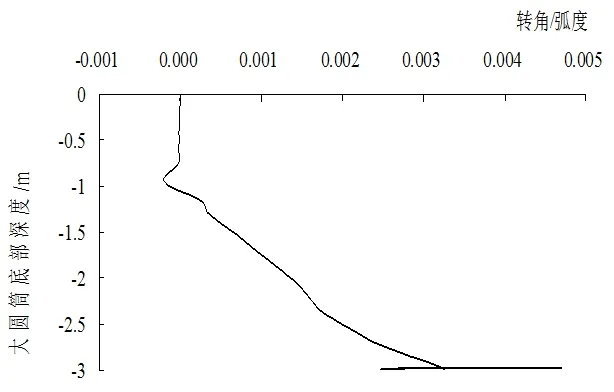
图6 自重贯入过程大圆筒绕Y轴转角

计算得到振动锤打入过程大圆筒的转角随时间的变化如图7所示。从图中可以看到，在开始时转角的数值有一个缓慢的增加，当增加到0.00527时，随着时间的增加，转角开始减小。产生该现象的原因是随着深度的增加，土体对大圆筒产生弯矩的抗力逐渐增大，同时水平荷载和弯矩逐渐减小，因此导致倾斜度的减小。最大转角对应的倾斜度为0.00527，根据 《水运工程施工与验收规范》（JTS257-2008）规定：单桩垂直度（桩尖对纵轴线偏斜）沉桩偏差验收要求为10 mm/m，即沉桩时垂直度是以1 %桩长来控制的（10 mm/1 000 mm=1/100），此计算结果满足该要求。

图7 振动锤打入过程大圆筒绕y轴转角

3. 安装现场的水动力条件对大直径钢圆筒贯入的垂直度的影响随贯入深度的变化而变化。在贯入深度较小时，大钢圆筒的倾斜度随着贯入深度的增加而增加；随着入泥深度的增加，土体对大圆筒产生弯矩的抗力逐渐增大，同时水动力导致的水平荷载和弯矩逐渐减小，钢圆筒的倾斜度随着贯入深度的增加而减小。

在现场施工过程中，可根据钢圆筒垂直度变化的特征合理确定施工方案，保证现场施工的顺利进行。

4 结论

本文采用数值模拟的方法考虑了水动力条件对大直径钢圆筒在贯入期间垂直度的影响,通过计算得到如下的结论,

1. 由于大直径钢圆筒在安装其间一直位于水面以下,大直径钢圆筒的存在对波面的影响不明显;但是水体在大圆筒附近和内部的流动方向受筒壁影响而发生了变化。在外界波浪和水流作用下，内部水体形成一个旋涡状的流动，产生了动水荷载以及水压力分布不均匀导致的力矩。

2. 受波浪周期性的影响，作用在大圆筒上的水平荷载和力矩也做波动变化，动荷载峰值，随着大直径钢圆筒入泥深度的增加，水平荷载和弯矩都逐渐减小，且入泥深度越大变化幅度越小。