工业纯钛TA2 拉伸及低周疲劳性能的各向异性

梁远长，常 乐，周昌玉

（南京工业大学机械与动力工程学院,江苏 南京 210000）

0 引言

工业纯钛是一种具有高比强度、低密度、耐腐蚀特性的材料，不论在航空、航天、舰船、核能等高科技领域,还是在化工、冶金、汽车、建筑、食品等民用工业领域,以及在医疗、体育休闲等民生领域均有广泛的应用[1-2]。工业纯钛作为各向异性的密排六方体结构（HCP）材料，其各个方向的力学性能差异较大，这种差异来自于冷轧产生的双峰倾斜基面织构及其独特塑性变形机制[3-4]。各向异性会显著影响金属板材成形性能及质量，如拉深成形过程凸耳的形成。此外，钛制设备例如钛制板式换热器、化工厂反应容器在频繁开停机、承受疲劳载荷的工况下会出现疲劳失效情况[5]，并且钛制设备往往同时受内压及轴向力作用，并非单轴应力状态，不同方向的疲劳性能存在差异。因此，研究工业纯钛拉伸力学性能及疲劳性能的各向异性具有重要工程意义。

国内外对于密排六方结构（HCP）材料拉伸及疲劳行为的各向异性研究主要集中在镁合金[6-7]，对于工业纯钛拉伸及低周疲劳性能的各向异性研究非常有限。刘定凯[8]等人讨论了不同厚度工业纯钛试样在RD 方向、RD-45°、TD 方向下的同一应变速率下不同力学性能差异以及不同轧制路径对板材组织及性能的影响。田晨超[9]等人采用动态接触式引伸计对纯钛板材静载拉伸下应变分量进行全程采集，比对分析横纵向下不同阶段塑性变形过程的各向异性，发现纯钛板材纵向（RD）的屈服强度较低，抗拉强度及断后伸长率则略高。常乐[10-11]为了了解循环不对称及控制方式对工业纯钛低周疲劳行为的影响，进行了对称应变和应力控制疲劳试验，从循环响应、微观组织演变和疲劳寿命等方面对不同控制方式下工业纯钛沿轧制方向和垂直轧制方向的低周疲劳行为进行了系统比较。由上述文献可见，对于工业纯钛力学性能的各向异性研究主要集中在RD、TD 方向，未充分考虑RD-TD 平面内取样角度对于材料力学性能尤其是疲劳性能的影响。此外，不同取样角度试样的拉伸本构模型以及疲劳寿命预测仍有待研究。

笔者通过不同取样方向下的准静态拉伸试验，获取工业纯钛各向异性的拉伸力学性能数据，利用常见的应变率相关的Hollomon 模型[12]及Johnson-Cook[13]模型描述其真实应力情况，并与试验得到的真实应力应变曲线进行对比。进一步对不同取向试样进行低周应变控制疲劳试验，以了解工业纯钛各向异性疲劳性能，并使用能量模型及Manson-coffin模型对疲劳寿命进行预测，为合理、安全使用钛制设备提供依据。

1 试验方案

试验材料为工业纯钛 TA2 板材，材料的化学成分见表1，在室温下进行试验，拉伸试样按照 GB/T 228.1-2010《金属材料拉伸试验》标准设计，疲劳试样参照GB/T 15248-2008《金属材料轴向等幅低循环疲劳试验方法》标准设计。拉伸试样的具体尺寸如图1 所示，疲劳试样的具体尺寸如图2 所示。拉伸及疲劳试样沿轧制方向（RD）、与RD 呈30°方向（RD-30°）、与RD 呈60°方向（RD-60°）及垂直轧制方向（TD）取样，具体试样排布如图3 所示。对四个加载方向（RD、RD-30°、RD-60°、TD）上均进行不同应变速率拉伸试验，应变速率分别为5×10-5、5×10-4、5×10-3s-1。然后对应变控制下不同方向试样进行不同应变幅值下的对称应变控制疲劳试验，加载波形为三角波，总应变幅值分别为0.4%、0.6%、0.8%、1.0%。试验在MTS809 试验机上进行，使用引伸计对实时应变进行测量。图4 为母材金相组织，可以看出母材由等轴晶粒组成。

图3 试样排布情况Fig.3 Sample arrangement

图4 母材金相Fig.4 Metallography of base metal

表1 TA2 的化学成分Table 1 Chemical compositions of TA2 %

图1 拉伸试样尺寸Fig.1 Tensile sample size

图2 疲劳试样尺寸Fig.2 Fatigue sample size

2 试验结果分析

2.1 拉伸行为研究

2.1.1 力学性能

图5 分别为屈服强度、抗拉强度、断后延伸率、屈强比随加载方向和应变速率变化情况。可以看出，不同取向试样的屈服强度随着应变速率的升高而升高，并且随着取样角度的增加，不同应变速率下材料的屈服强度增加。抗拉强度同样随着应变速率上升而增加，并且RD 方向的抗拉强度反而高于TD 方向。尽管RD 方向试样屈服强度较低，但是由于其应变硬化能力高于TD 方向，导致其抗拉强度更高[14]。断后延伸率随着加载方向的变化并不明显，随着应变速率的上升呈现下降的趋势。为了进一步综合评价不同取向试样的塑性变形能力，图5（d）进一步比较了屈强比的变化趋势。可以看出，屈强比随着加载方向由RD 方向变化到TD 方向时，屈强比呈上升趋势。屈强比为屈服强度和抗拉强度比值，通常来说，屈强比越小，当工作应力高于材料的屈服应力后，由于产生均匀塑性变形，某些应力集中部位的应力重新分布,可减缓或避免脆性断裂。因而材料均匀、塑性变形能力越强，越不易发生塑性失稳，材料塑性越好。

图5 TA2 拉伸力学性能随加载方向和应变速率变化Fig.5 Variations of tensile mechanical properties of TA2 with loading direction and strain rate

2.1.2 真实应力预测

考虑到拉伸过程中试验试样因为颈缩导致实际横截面积的变化，将TA2 拉伸的工程应力-应变曲线转变为真实应力-应变曲线，转换公式为:

其中 εt（MPa）为真实应力；εe（MPa）为工程应力；σt（MPa）为真实应变；σe（MPa）为工程应变。Hollomon 本构方程可以很好地描述应变速率敏感性和应变强化对TA2 均匀塑性变形阶段（强化阶段）应力-应变曲线的影响。表达式如下:

其中m是应变速率敏感性指数;n是应变硬化指数;K值是强度系数。m的值可以通过对TA2 真实应力应变曲线上不同点的真实应力和应变速率取对数，并进行线性拟合得到。n的值可以通过对真实应力应变曲线强化阶段选取合适区间，并对此区间的真实应力应变值取对数后进行线性拟合得到。将不同拉伸条件下的应变硬化指数n、应变和应力的值分别代入Hollomon 本构方程，可求出对应的强度系数K值。

在拉伸本构方程中，Johnson-CooK 模型本构方程凭借其形式简单的优点得到了较为广泛的应用，JC 本构方程的表达式为：

本构方程中包含4 个本构参量，分别为A，B，C，n，均为材料参数，可通过拟合求出。

基于试验数据，分别利用这两种模型描述工业纯钛的真实应力应变曲线。图6 给出了四个加载方向上不同模型预测结果与试验数据对比，可看出Hollomon 本构模型和试验得到的真实应力应变曲线几乎重合，效果较好，而Johnson-CooK 模型在某些强化阶段也能达到较好的预测效果。运用统计学参量相对误差来进行比较，其表达式为：

图6 Hollomon 本构模型和JC 本构模型预测情况Fig.6 Prediction results of Hollomon and JC constitutive model

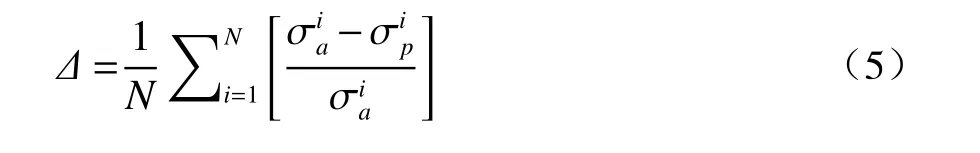
其中 σa(MPa)和 σp(MPa)分别是试验应力与模型预测应力，N为统计样本的总数。计算出Hollomon 本构模型和JC 模型的相对误差分别为0.146 1%和1.483 8%。Hollomon 本构方程拟合模型更接近材料的真实应力应变曲线。

2.2 疲劳性能

2.2.1 循环硬化/软化

图7（a）为轧制方向上不同应变幅下循环应力幅值随循环周次演变情况。横坐标为归一化的疲劳循环数（N/Nf)。由RD 方向不同应变幅下的应力幅值变化情况，可以看出应力幅值随着应变幅值的增大而增大，每个应变幅下的应力幅值随循环周次呈现一个三阶段的下降趋势，初始阶段迅速下降，然后缓慢下降，在失效阶段又迅速下降的三个阶段趋势，即三个阶段的循环软化。不同应变幅值下其他方向上的应力幅值随着循环周次演变情况同样呈现出循环软化特征。图7（b）比较了相同应变幅下，不同取向试样之间循环应力幅差异。根据前文拉伸试验结果可知，初始塑性变形阶段内，随着取样角度的增加，工业纯钛的屈服强度逐渐增加。因此，随着取样角度增加，材料的循环应力幅值也不断升高。

图7 循环应力幅与（a）应变幅值及（b）加载方向的相关性Fig.7 Dependence of cyclic stress amplitude with (a) strain amplitude and (b) loading direction

2.2.2 疲劳寿命

图8 为不同应变幅下疲劳寿命随加载方向的变化情况。可以看出，随着取样角度增加，工业纯钛的疲劳寿命逐渐减小。低周疲劳寿命与材料的塑性相关，塑性越好，疲劳寿命越长[15]。拉伸试验结果已经表明，随着取样角度增加，材料的塑性呈下降趋势。

图8 疲劳寿命随加载方向的变化情况Fig.8 Variation of fatigue life with loading direction

2.2.3 应变能密度

应变能密度可分为弹性应变能密度ΔWe+(MJ/m3)、塑性应变能密度ΔWp(MJ/m3)及总的应变能密度ΔWt(MJ/m3)，塑性应能密度ΔWp(MJ/m3)即迟滞回线所包含的面积，可通过对迟滞回线积分求出。Lin[16]等人修正了传统应变能计算公式，发现与塑性应变能密度相比，总的应变能密度更能反映材料循环变形中累积的损伤对于材料疲劳寿命的不利影响。总应变能密度和弹性应变能密度计算公式为：

其中，σa为应力幅值(MPa)；E为弹性模量(GPa)。

图9 为工业纯钛总应变能密度随加载方向和应变幅值变化情况。可以看出，随着加载方向由RD方向过渡到TD 方向，总应变能密度逐渐增加，说明累积的损伤同样随取样角度增加而增加，导致材料的疲劳寿命逐渐下降。

图9 总应变能密度随加载方向和幅值变化情况Fig.9 Variation of total strain energy density with loading direction and amplitude

2.2.4 低周疲劳寿命预测

首先使用总应变能密度来预测材料疲劳寿命，即

其中，Nf为疲劳寿命；k、c的值可以通过拟合获得，列在表2 中。图10 为通过总应变能密度预测结果与实际寿命的比较。可以看出，通过总应变能密度预测的结果大多处于两倍误差带内，但仍有少数预测结果处于两倍误差带外。

图10 基于总应变能密度的疲劳寿命预测与试验结果对比Fig.10 Comparison between fatigue life prediction by total strain energy density and experimental results

因此，进一步使用常用的Manson-coffin 模型预测不同取向试样的低周疲劳寿命。Manson-coffin模型的表达式如式（9）（10）所示。

表2 不同疲劳模型参数拟合值Table 2 Fitting values of different fatigue model parameters

图11 给出了试验疲劳数据和Manson-coffin 模型预测结果对比。可以看出，在不同加载方向上不同应变幅值的预测数据点都位于两倍误差带内，即Manson-coffin 模型可以更准确预测工业纯钛TA2应变控下不同方向的疲劳寿命。

图11 Manson-coffin 模型预测寿命与试验结果对比Fig.11 Comparison between predicted life by Mansoncoffin model and experimental results

3 结论

目前压力容器设计规范中仍将钛材按照各向同性材料处理，笔者通过室温准静态拉伸试验和对称应变控疲劳试验，研究了工业纯钛TA2 拉伸力学性能和低周疲劳性能的各向异性，得到了不同取样方向的拉伸本构及疲劳寿命预测模型，以期为相关钛制设备的各向异性设计提供数据支持及理论基础。主要结论如下：

1）工业纯钛TA2 拉伸力学性能具有显著的各向异性，随着加载方向由RD 方向过渡到TD 方向，屈服强度呈现逐渐上升趋势，而屈强比逐渐下降，即材料的塑性下降。

2）利用Hollomon 及Johnson-CooK 本构模型预测不同取向试样的真实应力应变曲线，定量对比结果表明Hollomon 模型预测精度更高。

3）工业纯钛TA2 的疲劳性能具有显著各向异性。尽管不同取向试样均呈循环软化特征，但随取样角度增加，循环应力幅值增加，总的应变能增加，导致材料的疲劳寿命呈下降趋势。

4）利用能量模型及Manson-coffin 模型预测不同取向试样的低周疲劳寿命，定量对比结果表明Manson-coffin 模型预测精度更高。