基于特征截面的薄壁梁耐撞性形貌优化设计
田轩屹
(广汽丰田汽车有限公司,广东广州 511455)
0 引言
薄壁梁由于其成本低、吸能高、质量轻已广泛应用于汽车设计中。在汽车碰撞过程中,薄壁梁结构作为汽车的主要承载部件,不仅需要吸收大量能量,同时也决定了碰撞过程中加速度和力的响应。薄壁梁的碰撞模式主要有轴向和侧向碰撞,其中薄壁梁的轴向变形所吸收的能量大约要比横向高一个数量级。因此,如何设计薄壁梁在轴向碰撞过程中的耐撞性能具有重要意义。
目前对于薄壁梁的轴向耐撞性研究主要集中在截面形状研究方面,常见的主要有圆形截面、方形截面等传统截面形状以及多胞截面等特殊截面形状。但是由于薄壁梁轴向压溃过程中,前端需要通过快速压溃吸收能量,后端需要通过抵制形变,因此不同位置所需性能不同,单纯的研究截面形状并不能有效提升耐撞性能和材料利用率。然而对于薄壁梁轴向形貌的研究大多停留在简单的直梁或者锥形梁,很少涉及其他复杂结构的薄壁梁,而实际工程应用的中薄壁梁一般为非等截面薄壁梁。
针对以上问题,本文采用分段3次Hermite插值方法对特征截面尺寸参数进行拟合,用于构建具有复杂形貌的薄壁梁结构。进而通过近似模型和多目标优化方法对各特征截面尺寸参数进行寻优,使得最终设计的薄壁梁形貌能更好地满足碰撞过程中不同位置的需求。
1 基于特征截面的形貌优化设计方法
基于特征截面的形貌优化设计方法通过从薄壁梁结构中选取若干特征截面(一般根据需求等距方式选定若干特征截面),并采用分段3次Hermite插值方法对各特征截面的尺寸参数进行拟合,进而得到完整的薄壁梁结构尺寸参数沿轴向变化曲线,如图1所示。

图1 尺寸参数变化曲线
通过修改各特征截面的尺寸参数值,不仅能够构造传统的直梁和锥形梁,同时还能够构造具有复杂形貌的薄壁梁结构。特征截面法构造梁类型如图2所示。

图2 特征截面法构造梁类型
同时,该方法将近似模型技术和多目标优化设计相结合,对各特征截面尺寸参数、薄壁梁结构厚度进行寻优,得到最优薄壁梁形貌。形貌优化设计方法流程如图3所示。

图3 形貌优化设计方法流程
2 有限元建模及试验验证
为建立有效的有限元模型,根据文献[9]所述方框梁正面碰撞试验建立有限元模型,并将仿真数据与试验数据进行对比。
2.1 几何模型及材料
文献[9]所述的方框梁正面碰撞试验几何参数如图4所示。方框梁总长310 mm,后端固定在长100 mm的夹紧装置上,夹紧装置约束方框梁末端的6个自由度。600 kg的刚性体以10 m/s的速度正面撞击方框梁。

图4 方框梁正面碰撞试验几何参数
方框梁采用高强度钢DP800,为了考虑高强度钢的应变率效应,通过高速拉伸试验机上进行了不同应变率下的单向拉伸试验,获得不同应变率下的真实应力-塑性应变曲线,如图5所示。

图5 DP800不同应变率下的真实应力-塑性应变曲线
2.2 有限元建模及验证
方框梁正面碰撞有限元模型通过Hypermesh建立,如图6所示。试件单元大小为3 mm×3 mm,几何尺寸与实际试件尺寸相同。试件后端约束6个方向自由度,前端刚性墙以10 m/s速度正面碰撞。

图6 方框梁正面碰撞有限元模型
图7为方框梁碰撞力-位移曲线,从曲线中可以看出试验与仿真数据吻合得非常好。试验与仿真碰撞力对比结果见表1,从表中可以看出两者误差均在可接受范围内,因此该有限元模型能够很好地反映方框梁正面碰撞过程,因此可以用于进一步优化设计研究。

图7 方框梁碰撞力-位移曲线

表1 试验与仿真碰撞力对比结果
3 方框梁耐撞性形貌优化
薄壁梁的耐撞性设计本质是一个多目标优化问题。要使薄壁梁具有较好的耐撞性能,必须使薄壁梁每单位质量结构吸收的能量最大,即比吸能()最大,其表达式为:

(1)
式中:为薄壁梁结构所吸收的能量,为薄壁梁结构的总质量。
比吸能代表了结构在发生碰撞过程中,其材料在能量吸收中的利用率。
同时,在设计过程中应尽可能减小最大峰值力,避免较大的冲击力对乘员的不利。
3.1 方框梁耐撞性形貌优化数学模型
针对方框梁形貌优化问题,选取等距5个特征截面进行研究,分别以距离方框梁左端0、77.5、155.0、232.5、310.0 mm处作为特征截面。由于方框梁四边相等,因此以各特征截面边长变量作为尺寸参数变量,如图8所示。

图8 特征截面及尺寸参数
在对方框梁进行尺寸优化的同时针对方框梁的厚度进行优化,并选取耐撞性指标碰撞峰值力及比吸能作为设计目标,因此高强度钢耐撞性形貌优化问题的数学模型可以表示为:

(2)
式中:为碰撞最大峰值力;为比吸能;、、、、分别为5个特征截面的边长变量;为方框梁厚度变量。
3.2 构建Kriging近似模型
Kriging近似模型具有局部估计的特点,使其在求解非线性问题时能够得到比较理想的拟合结果。薄壁梁碰撞过程是一个高度非线性的过程,因而通过采用Kriging近似模型能够构建具有较高精度的近似模型代替薄壁梁碰撞有限元模型。
3.2.1 试验设计
为了构建目标函数及约束条件的近似模型,需要通过生成有限的样本点,并根据样本点数据拟合得到目标函数及约束条件的近似模型。许多试验设计方法常用来生成样本点,拉丁超立方试验设计是一种约束随机生成均匀样本点的试验设计和采样方法,该方法能够通过很少的样本点反映整个空间的特点。而在拉丁超立方基础上提出的均匀拉丁方增加了均匀性判据准则,能够提升样本点空间分布的均匀性,如图9所示。并且对于非线性问题,均匀拉丁方能够构造出精度更高的近似模型。因此,采用均匀拉丁方构建300个样本点。

图9 拉丁超立方与均匀拉丁方样本点比较
3.2.2 误差分析
为了评估所构建的Kriging近似模型精度,在设计空间中随机生成了20个样本点对近似模型的4个常用误差分析指标复相系数(),相对误差(),最大相对误差()以及平均相对误差()进行分析,其计算公式为:

(3)

(4)

(5)

(6)

从图10和表2中可以看出,采用Kriging近似模型方法对目标函数与所构造的近似模型均具有较高的精度,因此能够代替真实仿真模型进行优化设计。

图10 Kriging近似模型各验证样本点的相对误差

表2 Kriging近似模型误差分析
3.3 多目标优化
NSGA-II在普通遗传算法的基础上采用非支配排序机制、拥挤距离计算和新个体比较操作等策略,求解Pareto最优解集,能够有效地解决多目标优化问题,并且能够同时对多个点进行评估,具有较好的全局搜索能力。采用该方法对以上建立的Kriging近似模型进行优化,其参数设置为:种群规模40,进化代数50,杂交概率0.9,杂交分布系数10,变异分布系数20。
薄壁梁耐撞性形貌优化Pareto前沿如图11所示,由图可以看出,两个优化目标之间是相互矛盾的,一个目标的优化必然导致另外一个目标的性能降低作为代价。因此多目标问题不存在唯一的最优解,而是多个最优解的集合。设计人员可通过设计方案倾向从Pareto前沿解中选取相应的最优解。若选择的最优解处于初始设计点与坐标轴的覆盖区域,可同时保证和均优于初始设计。

图11 薄壁梁耐撞性形貌优化Pareto前沿
为快速有效地从Pareto前沿解中选出具有良好综合耐撞性能的最优解,文中采用改进的最小距离选解法从Pareto前沿解中选取具有良好综合耐撞性能的最优解。改进的最小距离选解法在传统最小距离选解法的基础上对各目标进行了归一化处理,有效避免了最优解向数量级较大的一方偏离,使得最优解具有更好的综合性能。改进的最小距离选解法计算公式为:

(7)

(8)
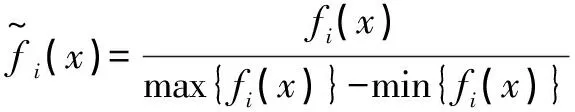
(9)

表3为优化前后特征截面及厚度对比结果,图12为优化前后方框梁形貌对比,由图可以看出优化后的方框梁具有更复杂的形貌,能够更好地满足薄壁梁在碰撞过程中不同位置所需不同性能的特点。

表3 优化前后特征截面及厚度对比结果 单位:mm

图12 优化前后方框梁形貌对比
图13为优化前后方框梁综合耐撞性能比较,由图可以看出,优化后的方框梁综合耐撞性能获得显著提升,其中下降43.48%,增加28.57%,因此说明所提出的方法是有效的。

图13 优化前后方框梁综合耐撞性能比较
4 结论
(1)为设计出具有复杂形貌的薄壁梁结构,通过分段3次Hermite插值对特征截面尺寸参数进行拟合,能够得到该尺寸参数沿轴向变化曲线。通过改变特征截面尺寸参数,使得尺寸参数沿轴向变化曲线改变,进而能够构造出具有任意复杂形貌的薄壁梁结构。同时对于不同的尺寸参数可以具有不同的变化曲线,因而使得薄壁梁结构的设计更具多样性。
(2)在优化设计过程中,采用近似模型方法代替形貌优化有限元模型,极大地减少了调用有限元模型次数,提高了形貌优化效率。同时采用多目标优化方法对各特征截面尺寸参数及厚度进行优化,使得薄壁梁结构达到最优。
(3)采用提出的方法对方框梁结构进行形貌优化设计。研究结果表明,优化后的方框梁结构综合耐撞性能得到了显著提升,因此该方法具有较高的工程应用价值。

