基于灰色马尔可夫模型的山东辖区海上险情事故量预测

王士鹏，周兆欣*，秦圻，马续仕，韩洋，邸光辉

1.山东交通学院 航运学院, 山东 威海 264200；2.烟台大学 继续教育学院, 山东 烟台 264000

0 引言

随着我国航运业的飞速发展，在籍运营船舶数量不断增长，海上船舶交通事故逐渐增多，给船员、船东造成较大的经济损失和人员伤亡，给海事部门的安全监管带来巨大挑战[1-2]。维护海上船舶交通安全，减少海上船舶交通事故成为经济发展的迫切要求。随着海洋强国等战略思想的提出和落实，全国港航经济发展潜力不断增强。山东辖区内水上交通运输能力高速发展，客货运吞吐量、海上交通流量及进出全省各沿海港口的船只呈稳固增长趋势，成为我国海上交通运输要道之一，其中成山头水道、长山水道、青岛港及日照港等水道、港口更是我国海域的重要水上交通要道。为满足国民经济发展需要，缓解海上交通安全监管压力，降低山东海域海上交通安全风险，采用科学、有效的方法预测辖区内的险情事故量，成为保障山东海域辖区海上交通安全亟需解决的课题。

科研人员对水上交通安全的研究主要集中在水上交通安全管理、水上交通冲突技术研究、水上交通安全系统和水上交通事故量预测4部分。在水上交通安全管理部分，李文华等[3]对长江某水域6 a的水上交通安全事故采用统计分析的方法研究事故发生的规律和原因，并提出相应的水上全权管理措施；王海燕等[4]从系统工程学的角度采用系统脆性理论构建人为因素致因理论模型，分析水上船舶交通事故中船舶安全管理系统与各子系统间的脆性关系；甘浪雄等[5]通过问卷调查法和熵权法分析调查结果，认为能见度和航道条件是最重要的影响因素。在水上交通冲突技术研究部分，Li等[6]运用引入导航交通冲突技术对长江口船舶航路(2002、2008年)进行对比分析，开发了可用于定量分析单个交通流对整个预防区安全影响程度的航行交通冲突数据自动采集系统；李松等[7]将交通冲突技术与船舶定线制警戒区优化设计相结合，提出了将警戒区小角度斜交航道交叉为大角度或正交等优化设计方法，减少警戒区交通流冲突点数量，降低冲突强度；谭箭等[8]通过分析我国水上交通事故评价水上交通安全现状，并将交通冲突技术运用到水上交通安全领域；谭志荣等[9]针对成山头水域商渔船碰撞事故频发的现象，采用Near Miss分布法，对成山头水域内商渔船冲突风险进行了可视化研究处理。在水上交通安全系统研究部分，齐迹[10]基于突变理论研究水上安全系统的演化行为，建立海上交通安全系统尖点突变模型；吴燕[11]针对目前水上安保系统存在的问题，如设备类型的差异大、测量参数繁多、各种报警频繁等问题，完成了水上安保系统的设计和初步应用；Zaman等[12]运用层次分析法在马六甲海峡设计了1种船舶交通安全自动识别系统并实现其功能。在水上交通事故量预测研究部分，范中洲等[13]采用灰色BP神经网络预测全国海上交通事故量，结果显示，基于灰色BP神经网络的预测模型精度更高；李铃铃等[14]建立灰色神经网络预测某水域的水上交通事故量，结果显示，此水域内的水上交通事故量呈下降趋势；张晓东等[15]采用基于负二项回归法的预测模型分析某港口及其附近水域的水上交通事故量，通过比较泊松回归和负二项回归2种概率分布模型回归的结果，确定基于负二项回归的水上交通事故分析与预测方法具有更好的适用性。

研究人员多侧重在安全管理、安全系统开发及水上事故量预测研究，研究涉及的海上区域较大，局部海域辖区预测研究较少，缺乏针对性。本文采用灰色模型(grey model，GM)中的GM(1，1)模型与马尔可夫理论相结合的灰色马尔可夫模型预测分析山东海域辖区的水上交通险情事故量，以期对未来山东海域的水上交通安全提供可靠的理论指导。

1 GM(1，1)模型预测山东海域辖区的海上险情事故量

灰色系统理论由我国著名学者邓聚龙教授创立[16]，是一种研究少数据、贫信息不确定性问题的新方法，主要研究内容有灰色系统的建模理论、灰色因素的关联分析理论、灰色预测理论和决策理论等。其中，GM(1，1)模型是灰色系统理论的重要组成部分，是1阶、1个变量的模型，适用于小样本数据预测，可实现对样本信息不足情况下的较高精度预测。为弱化GM(1，1)模型原始时间序列的随机性，在建立GM(1，1)模型前，先对原始时间序列进行累加处理，处理后的时间序列称为新生成序列。

1.1 GM(1，1)模型预测方法

灰色预测法是1种对含有不确定因素的系统进行预测的方法[17]。首先建立原始的非负时间序列A(0)，此序列下有n个观测值，序列表达式为

A(0)={A(0)(1),A(0)(2),…，A(0)(n)}。

通过累加过程后的新生成序列为

A(1)={A(1)(1),A(1)(2),…，A(1)(n)}。

以此类推可得GM(1，1)模型的微分方程[18]为

式中：a为发展灰数，也可称为待辨识参数；η为内生控制灰数，也可称为待辨识内生变量。

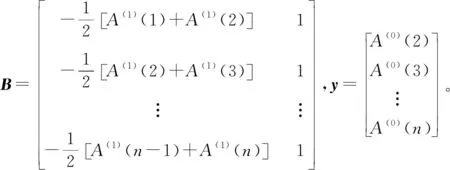
由式(1)求解微分方程，可得GM(1，1)模型方程

1.2 GM(1，1)模型预测数据处理

采用MATLAB软件处理数据，以统计的山东海域辖区内2010—2021年的海上险情事故量为原始非负时间序列[19]，得a=0.035 8，η=14.173，则GM(1，1)预测模型方程为

计算可得2010—2023年预测事故量与实际事故量的对比，如表1所示。

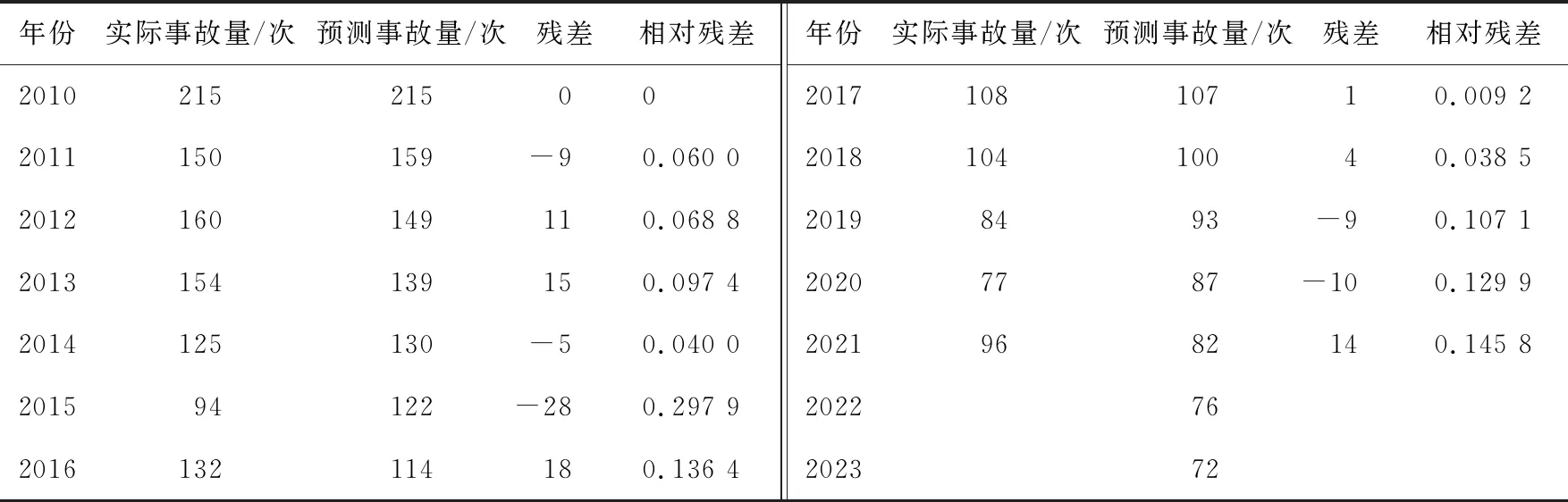
表1 2010—2023年预测事故量及与实际事故量的对比

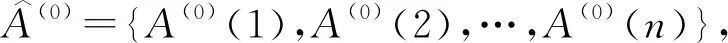
推算残差序列ε(0)的均值和方差分别为：

得到后验差比

C=s2/s1，

小误差概率

表2 预测精度等级对应P、C

式中：k为符合正态分布的概率误差系数，k=0.674 5。计算得P= 0.916 7，C=0.337 0。预测精度等级对应的P、C如表2所示。

由表2可知，此次预测结果P为良好，C为优秀，精度等级为良好。

2 灰色马尔可夫模型修正预测

为提高预测精度，准确描述未来山东海域辖区海上险情事故量变化趋势，将GM(1，1)模型与马尔可夫模型结合，采用MATLAB软件编程求解，得到不同的状态转移概率矩阵，使预测结果更准确，并分析事故发生原因及规律。

2.1 灰色马尔可夫修正预测方法

灰色马尔可夫模型可根据状态间的转移概率预测未来发展的情况[21]。根据标准划分不同的状态，用Z1，Z2，…，Zn表示，并建立状态转移概率矩阵

2.2 灰色马尔可夫模型修正数据处理

表3 状态转移次数

根据实际事故量与预测事故量之比划分状态区间：Z1=[0.77，0.90],Z2=(0.90，1.05],Z3=(1.05，1.20]。统计相关状态转移次数，如表3所示。

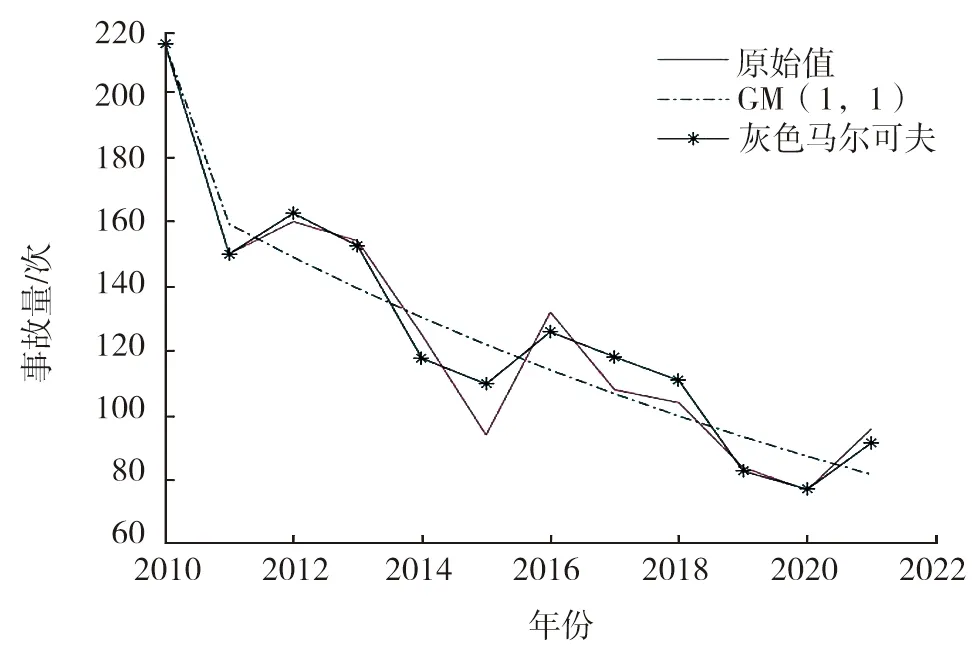
图1 模型预测结果与实际事故量对比曲线

由表3可得到状态转移概率矩阵

可知2021年海上险情事故量处于状态Z3，2022年处于状态Z2，2023年最有可能处于状态Z2，并将数据代入MATLAB软件进行预测，实际事故量、GM(1，1)模型预测结果和灰色马尔可夫模型预测结果对比如图1所示。

由图1可知：灰色马尔可夫模型的预测曲线比GM(1，1)模型更靠近原始值曲线。经计算，灰色马尔可夫模型的平均相对残差比GM(1，1)模型小5.240 8%，预测精度进一步提升。

预测结果显示，2022年山东海域辖区内的海上险情事故量约为86次，2023年约为81次，逐年稳定递减，这与有关主管机关及海事部门的有力监管密不可分，也反映了我国越来越重视海上交通安全管理，船员的整体航海素质和安全意识也在逐年提高。由图1可知交通险情事故量明显减小，但安全监管仍不容松懈。在恶劣天气条件下须及时发布有关气象信息，如在防范寒潮大风、海上大雾、防汛防台和防抗强对流天气等恶劣天气时，有关部门应及时提醒辖区内船舶避免涉险遇险，减小不必要的财产损失。

通过分析山东辖区内的海上交通险情事故发现，辖区内的渔船发生险情的现象时有发生，且占比较大。尤其当每年开海期时，渔船多为集群出航捕鱼，船只数量大、密度高、速度快，常发生商渔船碰撞事故，并伴有商渔船自沉、机损、进水、翻沉等现象。因此，应将今后的工作重点放在防范渔船等小型船舶险情和对渔船船员航行安全预警教育方面，提高渔船船员的整体航海素质和安全航行意识，使得涉渔险情得到有效地控制和预防。

3 结语

统计分析山东海域辖区2010—2021年的海上险情事故量，为减弱原始数据的随机波动性和时间性，采用GM(1，1)模型与马尔可夫理论相结合的灰色马尔可夫模型，预测山东海域辖区内未来2 a的海上险情事故量。由预测结果可知，采用灰色马尔可夫模型的预测精度比GM(1，1)模型高，可为提高山东海域辖区内的海上安全监管力度提供可靠数据参考。