基于多维动力指纹异常点识别的高桩码头损伤检测研究

肖 冰

(福建船政交通职业学院 福建 福州 350007)

引言

近些年我国进出口贸易呈现出了前所未有的繁荣盛况，港口码头建设也得到了迅速发展，其中高桩码头大量应用在港口中。现役的高桩码头受到撞击、腐蚀、疲劳、过载、地基不均匀沉降等影响，易对结构的健康状况造成危害，因此对高桩码头进行结构损伤检测，实时了解码头结构的健康状况已成为国内外研究的热点。[1-3]

目前常用的无损检测技术有探地雷达/透视雷达(GPR)、超声回弹综合法、红外热成像技术、冲击回波法等，其主要原理是利用超声波和电磁波等对结构的局部构件进行检查。因此不适用于检测码头整体结构，且无法实现实时监测。[4]因此，近年来许多学者开始研究如何运用动力指纹开展高效准确的损伤识别方法：天津大学李桂青提出了基于声波CT和应变模态结合的损伤诊断方法[5]；孙熙平首次提出了基于模态应变能的高桩码头基桩损伤诊断方法，得出模态应变能变化率对损伤单元有较强的敏感性，能够识别出高桩码头基桩不同工况下的损伤[6]；陆晶晶等采用基于连续介质的离散元方法(CDEM)对高桩码头结构进行数值模拟，得出码头结构破坏以及破坏程度的临界荷载。[7]但以上既有动力指纹在基于实测数据对高桩码头桩基进行损伤识别有着无法避免的缺点，如存在的噪声和试验误差，易造成错判、误判情况；对于损伤点的识别多基于目测法或简单拉伊达σ法则，在损伤识别中无法给出阈值，实现自动化识别等。[8]

为解决以上问题，本文提出了一种应对复杂工况下结构损伤识别的新方法——多维动力指纹异常点识别方法，该方法以既有动力指纹作为研究基础，融合多种动力指纹指标，构造结构测点的多维指纹向量，采用多维动力指纹向量空间的距离阈值判别取代目视检查法，实现损伤识别的自动化。

1 多维动力指纹损伤识别方法构建

1.1 多维动力指纹构造

通过实测数据损伤识别研究发现，结构损伤前后柔度变化量、应变能变化量、曲率模态变化量三者任何一个物理量在损伤位置均有明显变化[9]，因此本文选取柔度变化量、应变能变化量、曲率模态变化量三个动力指纹指标构造多维动力指纹体系，使损伤特征在多维融合中得到加强，压制无损处的干扰，使损伤位置更容易被识别。具体如下：

(1)

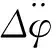
(2)

1.2 基于多维动力指纹的异常点识别

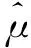
(3)

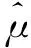
(4)

基于多维动力指纹向量空间的损伤识别方法具体流程如图1所示：

图1 基于多维动力指纹向量空间的损伤识别方法流程图

1.3 多维动力指纹损伤识别的自动化实现

本文采用COM实现Delphi与Matlab的混合编程，充分发挥Delphi灵活高效的程序设计能力和Matlab的强大计算能力，实现多维动力指纹的损伤识别自动化。[10]自动化识别部分交互界面如图2-4所示。

图2 高桩码头桩基损伤识别软件界面

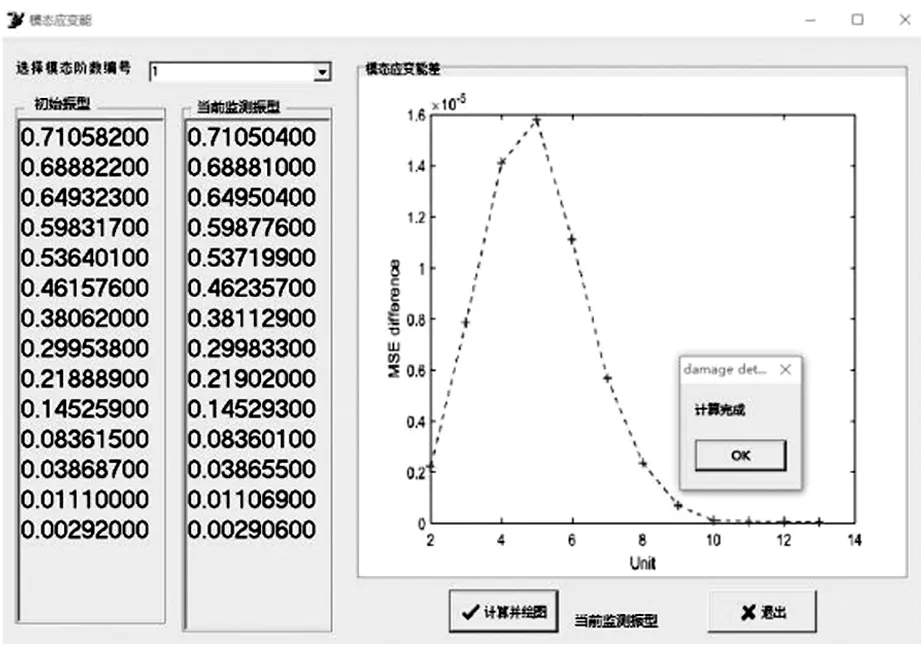
图3 单一动力指纹计算界面

图4 多维动力指纹损伤位置自动化识别

2 工程案例

根据高桩码头结构特点及调研情况设计高桩码头模型。在模型设计时根据研究内容对边界条件进行了部分简化，重点研究基桩泥面以上部分的动力损伤识别。考虑数值仿真计算与后续动力试验之间的验证和对比，数值仿真和动力试验采用同一模型，模型长2.05 m、宽0.9 m、高1.65 m，共3跨，排架间距0.65 m，码头前沿和中间为单直桩，后方为一对叉桩，桩身采用直径0.06 m、壁厚2 mm钢管桩，码头上部横梁、纵梁、面板采用混凝土浇筑，如图5。根据模型设计情况采用有限元分析软件Abaqus进行有限元数值模拟，所有部件均为实体单元，分别在模型前排2号、3号桩身模拟损伤情况，模型前排基桩编号如图6。

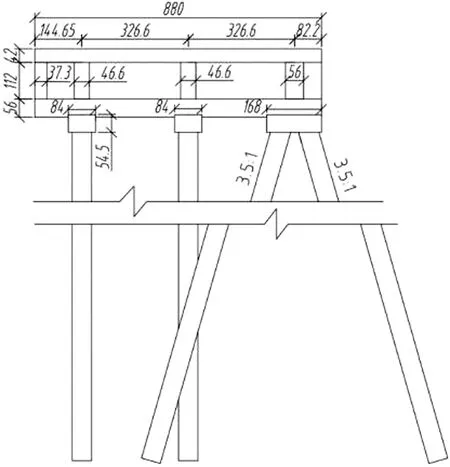
图5 模型断面图(单位：m)

图6 模型前排基桩编号图

根据高桩码头基桩常见损伤位置及损伤程度调研情况设置基桩损伤，损伤位置设置在2号桩5号段和3号桩19号段，损伤程度分别设置为刚度EI(E为弹性模量，I为截面惯性矩)减小5%、10%、20%、30%。(如表1、表2)

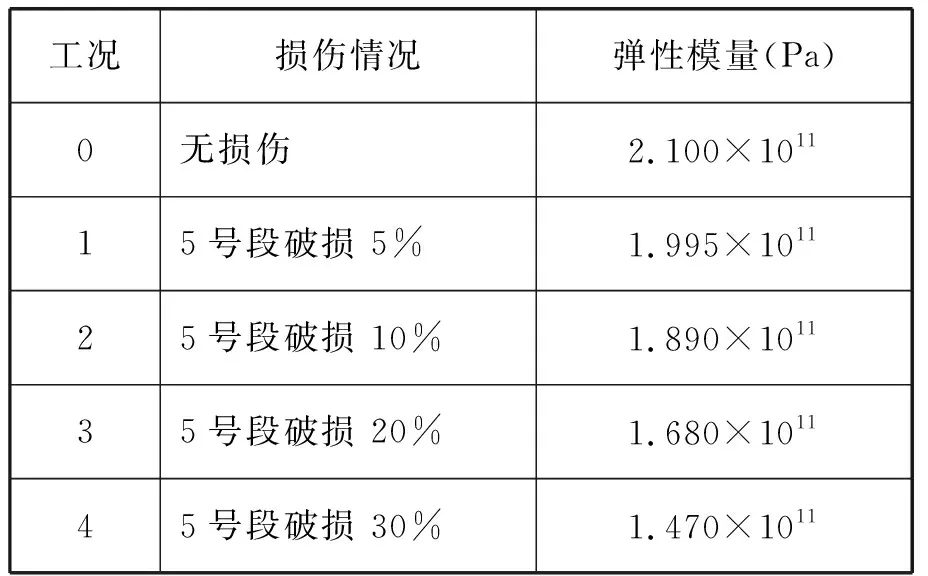
表1 码头模型2号桩损伤工况表

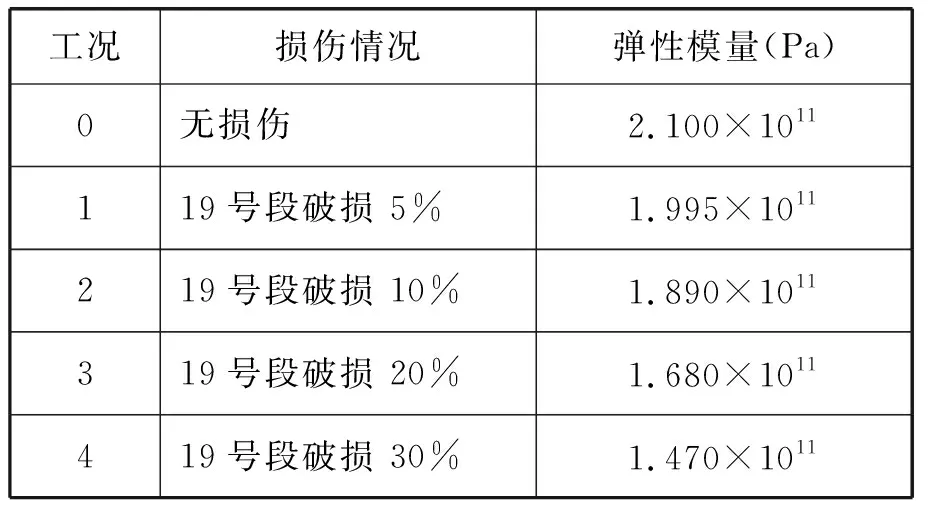
表2 码头模型3号桩损伤工况表

3 基于数值模拟的多维动力指纹损伤识别方法验证

3.1 多维动力指纹损伤识别方法正确性

模型选取的三个物理量中应变能横坐标为单元，柔度和曲率模态横坐标为节点。将每个结构段看作一个单元，单元编号与结构段编号相同，用原结构段的应变能代表单元应变能，用各单元上部节点的柔度和曲率模态代表单元的柔度和曲率模态。[11]

图7以2号桩为例画出了各单元的多维动力指纹空间分布。

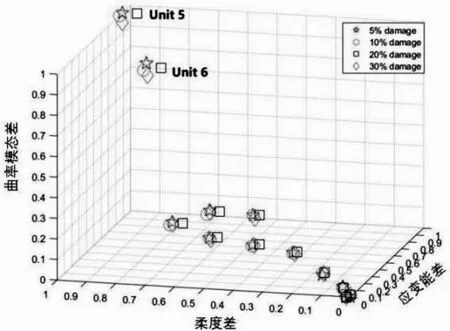
图7 2号桩多维动力指纹空间分布图

从图7可以看出损伤位置5号单元多维动力指纹离其他单元多维动力指纹最远，6号单元动力指纹由于在多维动力指纹融合过程中采用6号节点的模态柔度和曲率模态，同样受到了损伤的影响，离群也较远。

图8-图15列出了各损伤工况下基于码头桩基损伤前后有限元计算结果的多维动力指纹损伤识别结果。

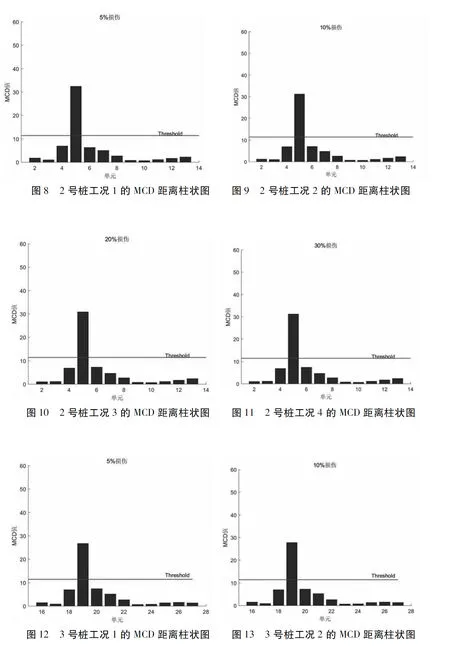
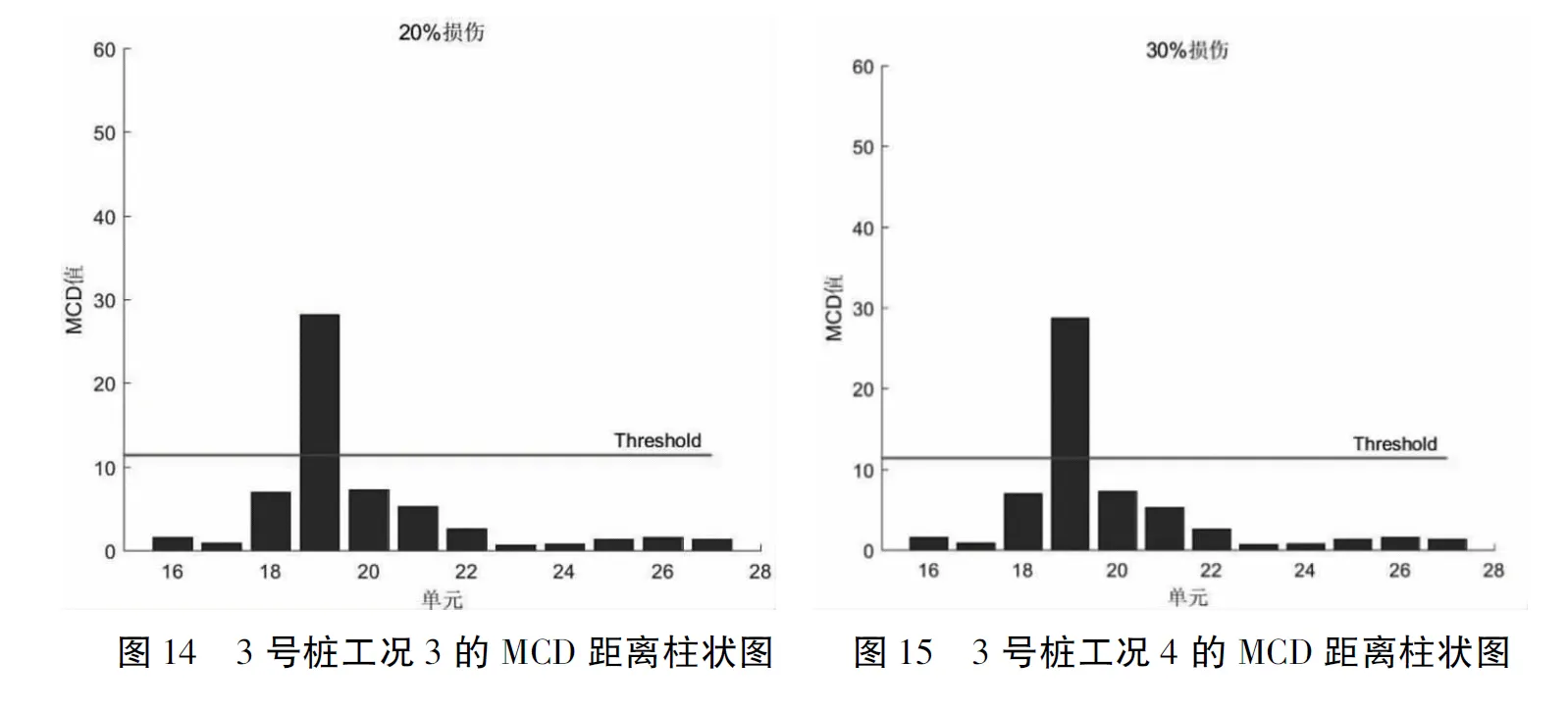
从图中可以看出，2号桩5号单元和3号桩19号单元MCD值大于阈值作为异常点被识别出来，可判断损伤，与实际情况一致。同时损伤单元MCD值远大于非损伤单元，损伤位置临近单元，由于受到损伤单元的影响，其MCD大于远离损伤区域。如图8中2号桩工况1的 5号单元 MCD值为32.4，其临近单元4号单元和6号单元 MCD值 6.9和6.3，其他单元MCD值均小于5，损伤单元MCD值为其他单元的4.5倍以上。由于多维动力指纹损伤识别过程对每种工况均作了归一化处理，所以不同损伤程度间的MCD值大小不具有可比性和相关性，每种工况下MCD 值仅作为该损伤工况下的判断依据。对于某根指定桩基来说其归一化后的不同损伤MCD值曲线形态具有一致性，但具体数值有差别，如 2号桩 5%和 10%损伤工况下5号单元的MCD值分别为32.4和31.2，因此，多维动力指纹损伤识别实现了自动化识别损伤位置，但其MCD值大小不反映损伤程度大小。

3.2 多维动力指纹损伤识别方法鲁棒性

利用Matlab函数 Wn=awgn(Wo , SNR', measured') 对各损伤工况下有限元计算结果分别添加100 dB、90 dB、80 dB、70 dB高斯白噪声，其中SNR为信噪比，Wn和 Wo分别表示有噪声的曲率模态和无噪声曲率模态，参数Measured是指在添加噪声前，先测量Wo的功率。抽取各工况下各信噪比下1000组数据使用多维动力指纹进行损伤识别，最终得到各工况下不同噪声下的损伤识别成功率如表3所示。

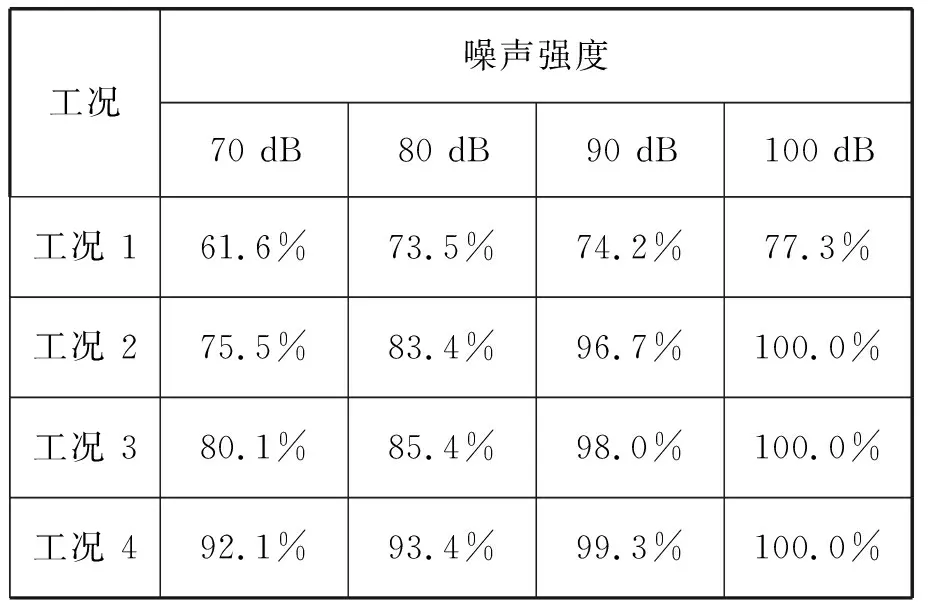
表3 各损伤工况不同噪声的损伤识别成功率

由表3可知，同种噪声影响下，损伤程度越大，成功率越高，这是因为损伤程度越大，其损伤特征越明显，受噪声影响越小。当损伤程度超过10%，信噪比大于80 dB时，损伤识别的成功率均大于80%；当损伤程度超过30%，信噪比大于90 dB时，损伤识别的成功率接近100%。随着量测技术的发展，目前市场大部分厂家设备信噪比优于90 dB，本文试验采用的系统信噪比为100 dB-130 dB，可见在当前试验条件下多维动力指纹损伤识别方法具有很好的鲁棒性。

随机抽取一组2号桩70 dB噪声下多维损伤案例，图16-图18为噪声下单一动力指纹损伤识别结果。

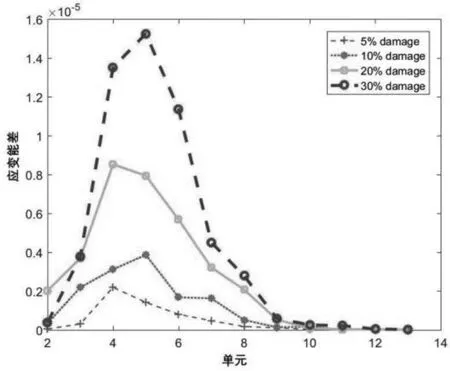
图16 70 dB噪声扰动下2号桩各工况应变能变化量 图17 70 dB噪声扰动下2号桩各工况模态柔度变化量

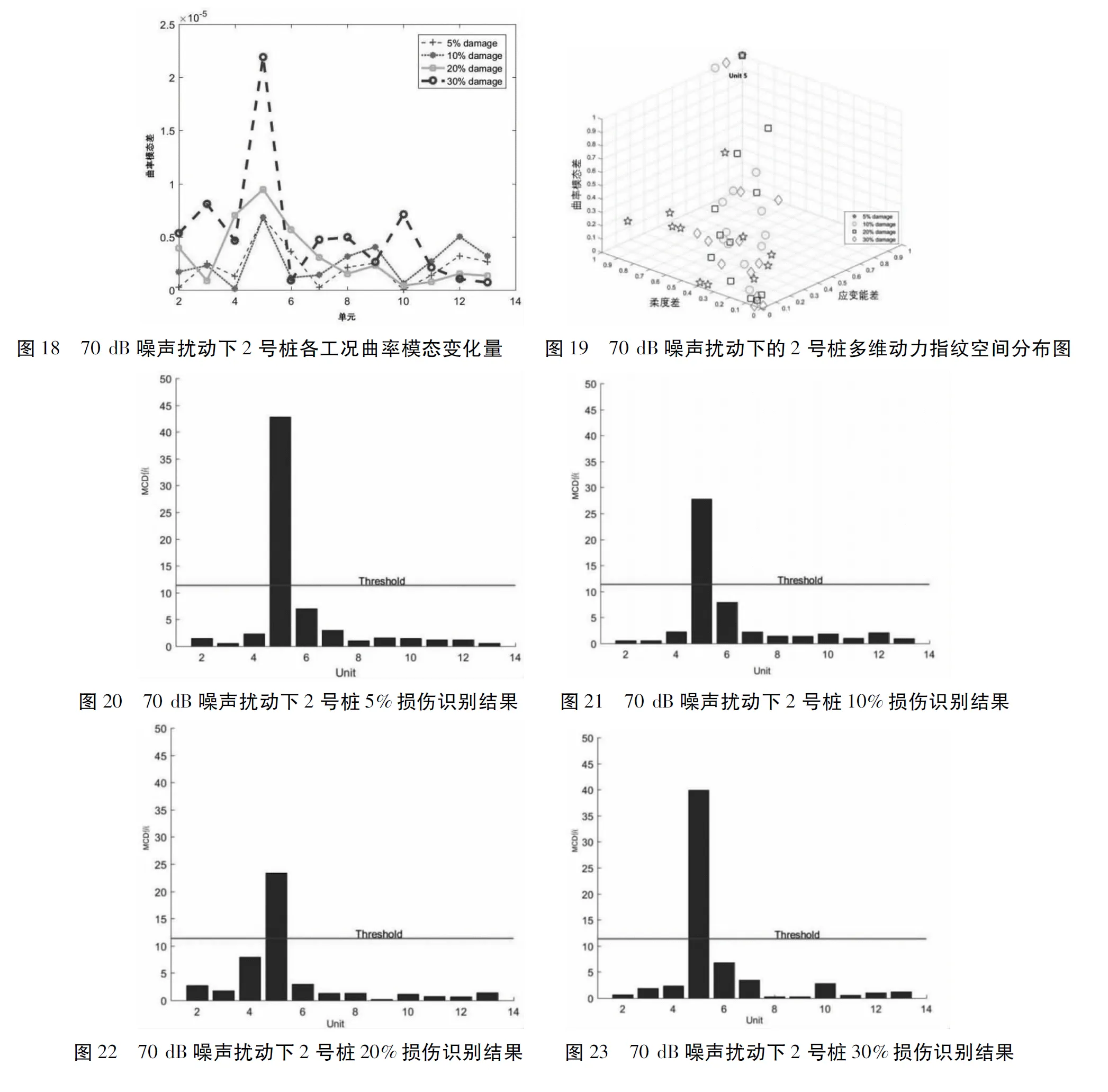
从图中可以看出，在噪声影响下单一指纹容易产生误判，如图16中5%和20%损伤下的4号单元、图17中10%损伤下的6号单元及30%损伤下的12号单元、图18中30%损伤下的10号单元均会误判为损伤单元；图19以2号桩为例画出了噪声影响下各单元的多维动力指纹空间分布，图20-图23列出了噪声影响下多维动力损伤识别结果，可以看出通过多元信息融合，5号单元作为离群数据被准确识别出来。

4 基于动力试验的多维动力指纹损伤识别方法验证

高桩码头物理模型完全按照有限元模型参数制作，为了方便和有限元计算结果对比，模型试验的三维方向、桩号、桩身分段编号、节点编号与数模保持一致。码头试验模型如图24。

图24 码头试验模型图

图25-图32列出了基于码头动力试验的多维动力指纹损伤识别结果。

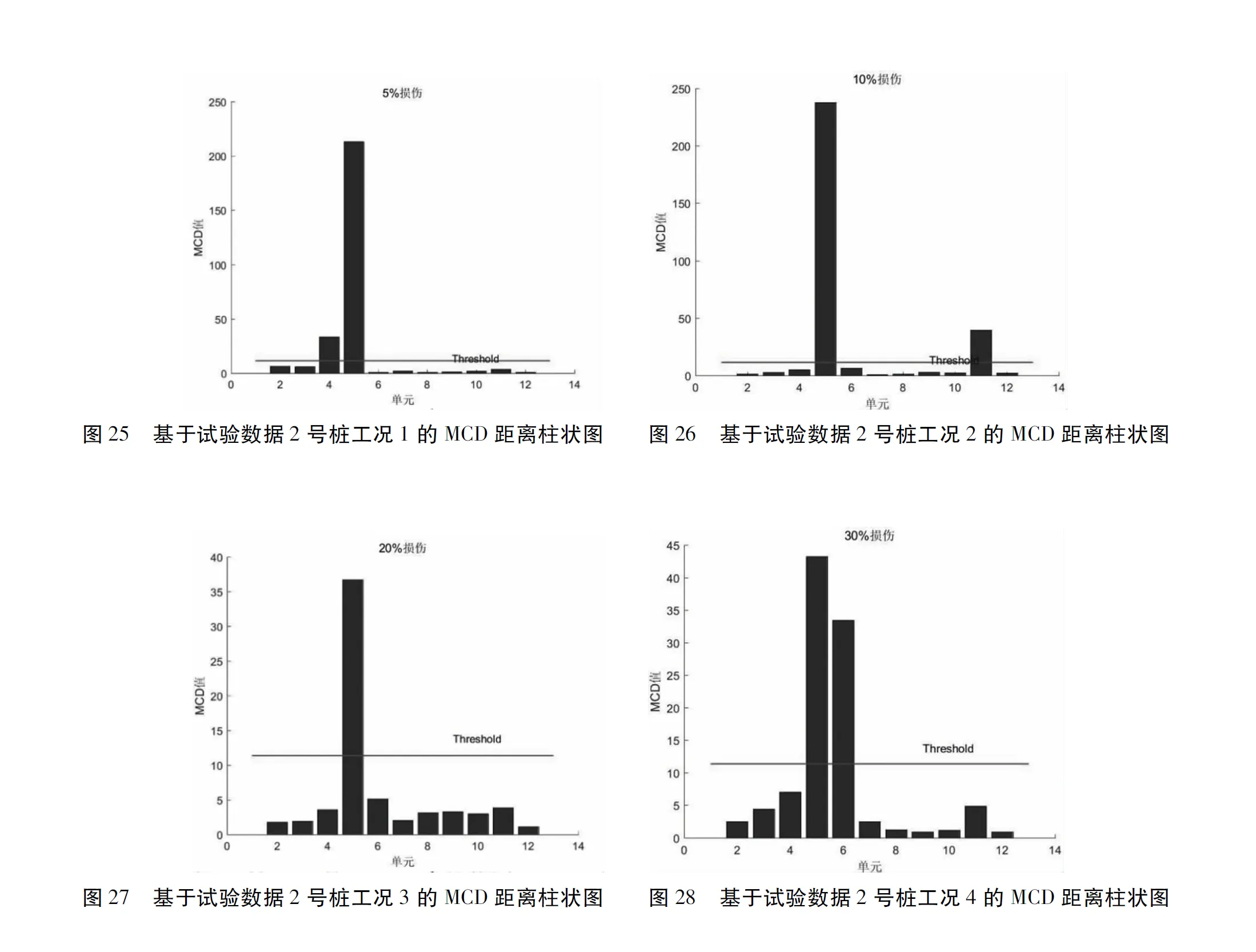
从图中可以看出，2号桩5号单元和3号桩19号单元MCD值均大于阈值作为异常点被识别出来，可判断损伤，与实际情况一致。由于实验误差和噪声的存在，个别工况的临近单元MCD值大于阈值也被识别出来，如图25中2号桩工况1的4号单元、图28中2号桩工况4的6号单元、图29中3号桩工况1的20号单元，这是由于临近单元本身受损伤单元的影响较大，加上存在噪声易造成MCD值超过阈值，由于损伤识别是为找到疑似损伤区域，因此临近单元被识别出来具有合理性，不影响试验损伤识别。可以看出，经过多维融合后损伤位置的特征得到加强，无损处的干扰经过融合之后被压制，基于MCD异常点检验算法的多维动力指纹损伤识别方法整体损伤识别质量和准确率比单一动力指纹损伤识别均有很大程度提高，表明该方法运用在物理模型动力试验上同样具有优越性和强鲁棒性。

5 结语

5.1提出了基于多维动力指纹向量空间的损伤识别方法，选取柔度、应变能、曲率模态构建多维动力指纹向量，运用最小协方差行列式的Mahalanobis距离异常点识别进行损伤定位，给出了基于MCD异常点检验算法的多维动力指纹损伤识别方法的详细实施步骤，该方法具有高效、快速、鲁棒的优点，同时用阈值判断取代通常采用的目视检查法，准确识别损伤位置，实现在高噪声复杂实际工况条件下损伤识别的自动化。

5.2通过高桩码头有限元模型计算数据，运用基于MCD异常点检验算法的多维动力指纹损伤识别方法进行损伤识别，准确识别码头桩基损伤位置，表明该方法的正确性；通过有限元计算数据基础上分别添加100 dB、90 dB、80 dB、70 dB高斯白噪声，损伤识别的高成功率展现了该损伤识别方法的强鲁棒性。

5.3基于码头动力损伤试验运用本方法进行损伤识别，仍准确识别了高桩码头桩基损伤位置，与既有动力指纹识别结构相比，该方法损伤特征在多维融合中得到加强，无损处的干扰经过融合之后被压制，使损伤位置更容易被识别，展现了该方法的强鲁棒性。