基于发电计划和设备检修计划的实时调度智能安全校核

段秦尉，潮 铸，唐旭辰，黄红伟，李 展

(1.广东电网电力调度控制中心，广东 广州 510080；2.北京清大科越股份有限公司，北京 100084)

0 引言

机组检修对于电力系统保持可靠稳定的供电十分重要，一般机组检修计划需要考虑可靠性、经济性等内容[1]。另一方面，机组检修与机组调度计划密切相关，影响着机组的检修调度安排。在实时调度背景下，更需要密切跟踪和安排机组的检修计划，满足网络正常运行和事故时的稳定性。

目前,已有的研究主要针对单独检修调度的优化，文献[2]研究了考虑梯级水电耦合特性的水火电联合检修优化；文献[3]论述了电力市场环境下发电机组检修规划研究；文献[4]提出了水火电机组年度检修计划安排的实用优化模型；文献[5]提出了基于中长期风电光伏预测的多能源电力系统合约电量分解模型，模型中计及了机组检修内容。但上述文献和已有研究中对机组检修和实时调度的联合建模仍有待进一步深入。

为此，本文针对发电计划和设备检修计划对实时调度的校核影响进行了分析。针对机组检修与安全约束调度的关系和步骤进行了梳理。建立了以安全调度为目标以及以竞标机组为目标的多目标检修计划优化模型，约束条件以直流潮流作为实时在线校核。利用二进制遗传算法以及原始对偶内点法对模型进行联合求解。

1 机组检修与安全约束实时调度

传统机组检修与调度联合计划的流程决定了系统运行的安全性和稳定性。发电系统运行商根据其利润和系统可靠性的关系确定机组检修计划和发电计划，该计划将会上传至调度中心，用于评估系统的可靠性和安全约束。

在该流程中，系统的安全性能、经济性能，以及机组检修计划的公平性则通过检修计划得以保证。具体分为如下步骤：

a.发电系统运行商根据机组运行状况和电网调度要求收集相应数据资料。

b.调度中心根据检修计划执行安全约束经济调度，同时满足网络安全约束、最大化系统可靠性。

c.调度结果则反馈至发电系统运行商。发电系统运行商根据其利润曲线评估调度中心制定的检修计划，并根据检修时间窗口制定相应检修机组标的。

d.检修标的则传达了发电系统运行商对于检修时间窗的检修意愿。

e.当发电系统运行商所提供的标的不能得到满足时，调度中心则停止其检修计划，并通过其他机组的检修要求确定检修调度问题。检修标的则同时加入目标函数进行优化。

f.如果能够在其他机组调度和检修计划中得到最优解，则最终实现机组调度和检修要求。

g.如果在求解过程中没有得到最优解，则该机组制定的检修计划需要进行履约。

h.最终得到的竞标机组和非竞标机组都需要遵循调度中心以及发电系统运行商制定的联合计划。

2 考虑安全约束的机组检修调度优化模型

2.1 目标函数1(基于安全调度的机组检修计划)

机组检修计划目标函数为最大化系统可靠性、满足系统运行和维修约束。可靠性用系统备用水平表示，具体表达式为：

(1)

(2)

满足的约束条件为：

St≥PDt+Rt

(3)

(4)

(5)

(6)

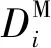
考虑到N-1的要求，系统需要在机组检修调度中保持成本最小。其中，约束条件中考虑到实时调度的要求，采用直流潮流的形式，即

(7)

约束条件为：

Bb·Θ+PDt-cGPict=0

(8)

|Bf·Θ|≤Fmax

(9)

(10)

Pimin≤Pict≤Pimax

(11)

2.2 目标函数2(基于竞标的检修组合)

在第2阶段，机组检修计划竞标用于校核检修计划。发电系统运行商提供的检修竞标表示了在机组检修窗内的检修意愿。在本文研究中，检修竞标可以为正、负、零。在检修窗内的正标意味着发电系统运行商更愿意在检修时间范围内对机组检修计划进行支付。竞标平衡方法可用于避免系统发电商利用所投标的误导系统调度中心，在该方法中，所有检修时间范围内的检修机组标之和应当为0。

第2阶段的目标函数也包括机组检修的可靠性以及经济性。在整个检修周期内，可靠性指标与第1阶段目标函数相同。在经济性指标中，基于竞标的目标函数则表示了机组检修计划检修标的的成本，即

f3=max(αβf1+f4)=

(12)

πit为机组i在时间t的检修计划标的；NGM为参与检修机组数量；α和β均为权重参数。

3 求解算法

本文选择利用二进制遗传算法以及原始对偶内点法对所提出的模型进行联合求解，能够有效解决这类非凸优化问题。二进制编码遗传算法用于求解主模型、原始对偶内点法求解最优经济调度问题。

3.1 初始种群生成

二进制编码遗传算法首先确定初始种群，采用随机生成机制。在遗传算法中，种群是作为问题的可能解进一步优化的。每个解编码为染色体，为保证足够的收敛性，需要对染色体的编码和译码进行明确。本文中，每个机组的检修时间起点X作为决策变量，X包括NGM行、T列。本文的染色体矩阵为

(13)

3.2 适应度计算

为比较每代种群中的求解结果，目标函数需要计算适应度，通过相应的求解步骤对染色体以及适应度函数进行求解。算法的过程如下：

(14)

(15)

(16)

(17)

Fmax为最终解中限制无效染色体的一较大负数。最终总的适应度函数计算式为

F=f1+f3-PF-PFres

(18)

算法求解流程如图1所示。

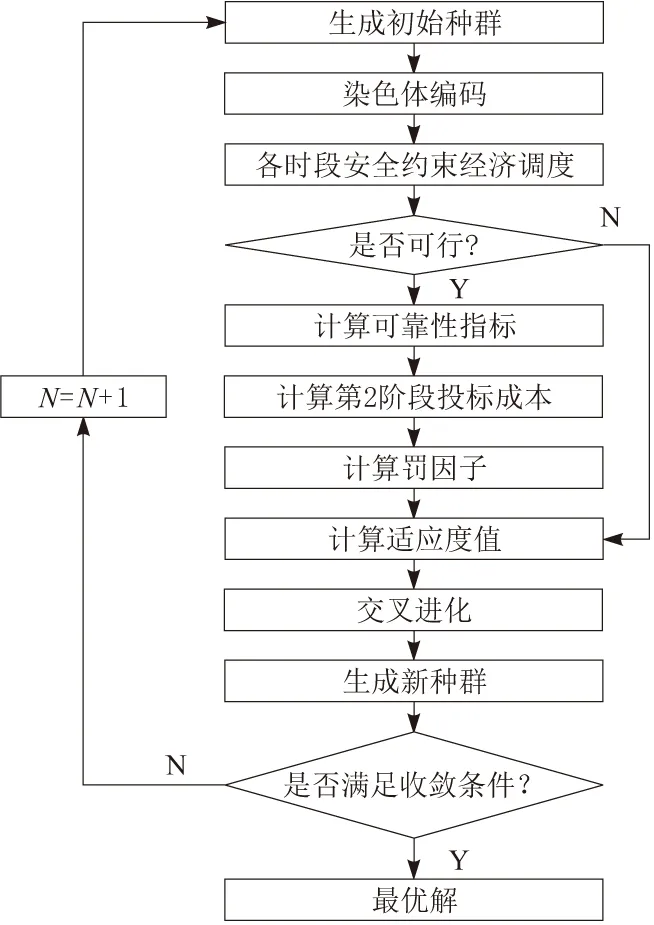
图1 算法求解流程

3.3 进化

二进制编码遗传算法需要进行种群选择、交叉和变异。

种群选择是从下一代生成的种群中选择较优结果，基于每一个体的适应函数进行选择。在本文中，选择轮盘赌方法对适应度较高的个体进行选择。

交叉是根据遗传学2个体之间交配的原理进行种群之间个体的生成，交叉运算能够使得种群朝着有利于个体发展的空间搜索方向进行。在本文中，2个体之间的交叉包括2点交叉和窗口交叉。前者主要是针对不同概率下2个体父代之间的运算；后者主要是包括矩阵中行和列的交叉变化。

变异操作是交叉完成后的下一步操作。在本文中，标准变异概率为Pm，通过随机选择进行生成。

个体修复是针对含有发电机检修约束的步骤，在本文中，修复算法是针对交叉和变异产生个体的运算行为。该步骤能够检查个体对约束条件的满足与否，如果出现不满足的情况，则需要对个体进行修复。当前个体以及新一代个体都需要利用修复机制实现个体的下一代更新。

3.4 判断收敛性

当算法生成的个体达到某一固定值时，算法判断收敛性之后则结束运算。最优解中的最佳染色体个体通过解码得到最终的检修调度结果。

4 算例分析

4.1 系统说明

本文选取30节点系统[6]进行仿真分析，如图2所示，仿真环境为MATLAB2014b。该系统包括6台机组和41条输电线路。

图2 30节点系统

机组检修计划如表1所示。

表1 机组检修计划

系统年内周负荷如图3所示。

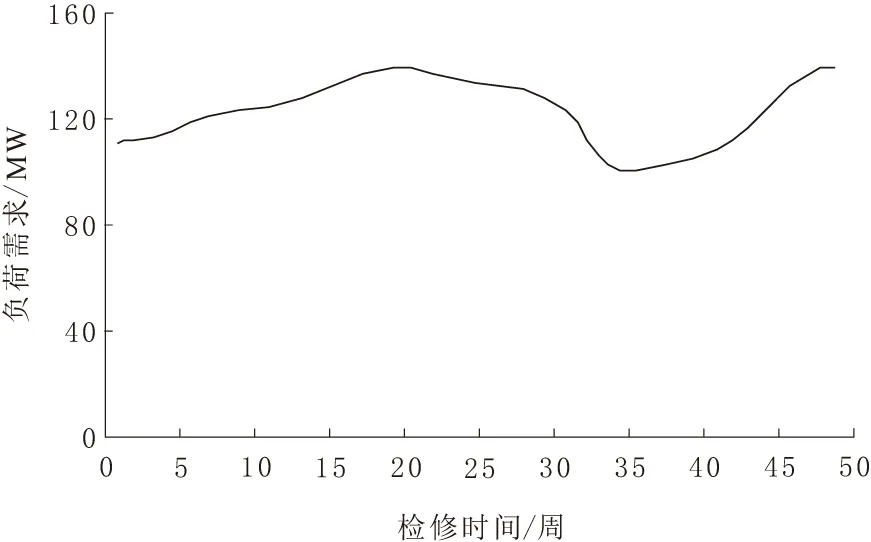
图3 负荷需求

停电线路1-2、1-3、2-4、3-4、2-5、2-6、4-6、5-7均考虑N-1故障。

本文考虑3种情景：

a.所有发电商接受阶段1的调度计划，即目标函数f1。

b.所有发电商均不接受阶段1的调度计划，即目标函数f4。

c.N-1故障下机组检修计划，即考虑f2。

4.2 算例分析

4.2.1 情景1

在情景1中，调度中心根据安全约束基础组合和检修计划确定机组检修安排，并传送至发电运行商。如果发电机组接受所提出的检修计划，则最终确定为该检修计划执行。否则，检修竞标则需要由发电系统运行商发起，通过调度中心对所投标的进行统一安排。在这种情况下，假设所有检修机组均能够接受调度中心提出的安全约束检修计划，并最终确定为机组检修计划。

利用遗传算法对模型进行求解，得到结果如表2所示。平均求解时间为3 000 s。

表2 求解结果

在检修计划中，机组3和机组6分别于第1周和第2周进行检修。系统负荷也与本文所求解得到的机组检修计划相匹配，可以看出负荷水平与检修计划的关系。值得注意的是，负荷水平较低时以及备用水平较高时，均为检修计划开始周期。由于检修机组均接受安全约束调度结果，因此，在这2种情况下进行检修对系统影响最小。

基础情景下的系统备用如图4所示。在检修计划开始时系统备用有所下降，所求解得到的检修可靠性指标为0.046 7 周/MW。

图4 系统备用曲线

4.2.2 情景2

在情景2中，调度中心首先对检修计划进行安全约束校核，结果如情景1所示。与前者不同的是，检修机组均不能够接受此计划，因此调度中心则需要利用发电系统运行商提供的检修竞标，重新安排机组检修计划，得到阶段2的模型。3号(黑色条纹)和6号(灰色条纹)发电机组的投标结果如图5所示，说明了检修机组在每周检修活动情况。对于机组6来说，16～24周最适合检修。根据所投标的，调度中心进行第2阶段机组检修约束优化。

图5 机组竞标结果

本文考虑α=1，β=10 000，该系数是对系统可靠性和系统经济性的折衷。求解结果如表3所示。平均求解时间为1 300 s。在α=0时，可靠性则被忽略，仅需要考虑竞标结果；在α=1时，能够较好地满足可靠性要求和经济性要求。

表3 求解结果

机组检修计划求解结果如表4所示，在最终结果中，机组3和机组6检修的时间为第25周和第24周。对于机组6来说，第24周进行检修是最佳结果；对于机组3，25周不是最佳的检修标的。这主要是考虑到系统目标函数中可靠性因素的影响。这一结果表明本文方法能够有效折衷检修成本以及可靠性指标。总的竞标成本为1 500元，可靠性指标为0.030 0 周/MW。

表4 检修计划

4.2.3 情景3

在考虑故障情况时，机组3和机组6的检修周期由原先的25和24变为9和1。同时，总检修成本则相比基础情景削减了30%。可靠性指标为0.028。该情景说明了考虑紧急故障检修，对于求解结果以及系统稳定性具有较现实意义。目标函数求解结果如表5所示。

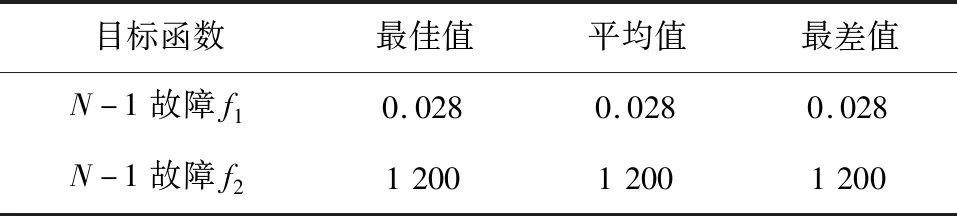
表5 求解结果

5 结束语

本文提出了基于发电计划和设备检修计划的实时智能调度安全校核流程和方法。通过仿真分析可以看出，本文方法能够有效提升调度中心以及发电商之间的耦合关系，并且能够检验在故障情况下机组检修计划以及发电调度的平衡关系。

通过本文所提出的多目标优化函数，得到各目标函数的最优值，同时可以确定机组在故障情况下以及正常运行时检修计划的变化关系，考虑故障情况下，机组的检修成本有所下降，并且可靠性指标有所提升。说明了本文方法的有效性和适应性。