基于响应面法的管线平板闸阀浮动阀座结构参数多目标优化

黄晓云， 夏胜建， 全 军， 张晓忠， 陈晓雷， 戴雄浩， 吴 静， 陈 浩

（保一集团有限公司， 浙江 温州 325000）

管线平板闸阀是石油、 天然气等输送管道系统的主要组成设备，应用越来越广泛［1-2］。 管线平板闸阀是一种关闭件为平行闸板的滑动阀， 通过旋转阀杆螺母带动闸板上、下运动实现输油、输气管线的启闭。 浮动阀座- 闸板密封结构是管线平板闸阀的主要密封结构之一［3-4］，其可靠性与整个管道系统安全性紧密相关。

文献［5-7］中指出，相较拓扑优化和形状优化而言，尺寸优化是最简单的结构优化方式，更易快速实现工程结构的降本增效， 是设备轻量化设计的重要手段。 而目前国内的阀门设计大多停留在经验设计阶段。

为此，本文以NSP6-Class300 硬密封管线平板闸阀的浮动阀座-闸板密封结构中浮动阀座结构参数优化为研究重点进行多目标参数优化，采用有限元分析软件对浮动阀座-闸板密封结构的刚度、强度、接触应力以及灵敏度进行分析。 利用对浮动阀座主要结构参数的敏感性分析和响应曲线分析，通过响应面法达到降低应力集中、减轻质量及提高使用寿命的优化设计目的， 实现浮动阀座结构参数的快速设计。

1 浮动阀座结构参数优化理论分析

1.1 中心组合设计法

设定自变量的初始值及变化范围之后， 就确定了试验的样本空间， 取样时选取的设计点应具有代表性， 尽可能以少的点数来最大限度地反映出样本空间数值特点。

中心组合设计法 （Central Composite Design，CCD）［8］是被广泛运用的一种取样方法，该方法中每个自变量都有5 个水平， 即β、-β、0 、1及-1， 中心点保证了一致精度， 轴向距离中心点±β 处为极值点。

三因子试验的CCD 取样设计点见图1。 由图1 可以知道， 正方形中心点保证了所定义单位距离的区域内所预测的优化值具有相同的方差，三角形极值点扩展了设计区域， 圆形点用于估计一阶项和交叉项。

图1 三因子试验CCD 取样设计点

为了控制设计点的数量，CCD 通过引入析因系数F 来剔除部分对角线上的点， 这样就能在保证响应面精度的前提下使设计点的数量最少。 自变量与设计点数量的关系见表1。

表1 自变量与设计点数量关系

1.2 响应面法

响应面法是一种应用广泛而高效的优化分析设计的方法。 该方法的本质是根据预设计点得出的确定性试验结果拟合出1 个响应面函数=（X1，X2，…，Xn）=0，以此响应面函数近似代表真实的功能函数z=g（X1，X2，…，Xn）=0。 拟合函数形式的选择， 既影响着拟合精度， 又决定着计算效率。利用响应面法进行分析设计，得到的结果可以为结构参数的快速优化设计提供基础。

实际工程中多采用全二阶多项式去逼近高阶隐式功能函数，其一般形式为：

式中，a0、ai、aij为待定系数，ε 为随机误差。

式（1）的待定系数共有（n+1）（n+2）/2 个，待定的系数矩阵可以通过最小二乘法得到。 在自变量比较多的情况下， 含交叉项的全二阶多项式计算量比较大。

一般采用决定系数R2和均方差σRMSE这2 个指标来评价响应面预测能力， 这2 个参数的计算公 式 分 别 如 下［9］：

式中，zi、分别为设计点观测值、响应面函数预测值。

1.3 偏移哈默斯利抽样技术

设定样本点数N 后， 对于一个n 维问题，非负数N 能够展开为N=a0+a1p+…+an-1pn-1（其中p为质数，a∈［0，p-1］）， 由此可以得到其构造函数表达式为：

首先选取质数序列p1＜p2＜…＜pn-1， 然后构造Hammersley 序列样本点为(i/N,ϕp1(i),ϕp2(i),ϕpn-1(i))，其中i=0，1，2，…，n-1。

偏移哈默斯利抽样时， 将以上所有数据样本点整体偏移Δ=N/2，是为了达到样本数据点能够均匀分布在试验空间中心周围的目的， 得到多目标优化初始种群。

2 浮动阀座-闸板密封结构分析

2.1 参数化模型建立

浮动阀座和闸板的结构分别见图2～图4，其上开设有导流孔、弹簧孔等。 浮动阀座-闸板密封结构的设计温度为常温。根据浮动阀座结构，选取密封面外径R1、密封面中径R2、密封面内径R3、浮动阀座厚度D1及密封面宽度D2这5 个主要结构参数作为自变量，初始数值分别为，R1=162 mm、R2=157 mm、R3=152 mm、D1=37.5 mm、D2=5 mm。 以密封结构最大接触应力、最大等效应力、总变形量以及质量为优化目标。

图2 浮动阀座二维结构

图3 浮动阀座三维结构示图

图4 闸板结构示图

2.2 静力学分析

浮动阀座和闸板的材料均为1Cr13， 该材料的特性参数为，泊松比0.3、弹性模量220 GPa、密度7.75 g/cm3、屈 服 强 度345 MPa、 拉 伸 强 度540 MPa［10］。 浮动阀座- 闸板密封结构的质量为21.1 kg。

利用静力学分析模块对浮动阀座- 闸板实体单元进行网格划分， 对重点关注的部位进行网格细化［11-12］，见图5 和图6。

图5 浮动阀座-闸板密封结构整体网格划分

图6 浮动阀座-闸板密封结构接触对网格细化

在考虑硬件运算能力和计算时间的前提下，将浮动阀座- 闸板密封结构总共划分为网格节点1 038 019 个、网格单元721 547 个。 划分的平均网格质量为0.835 81，该网格质量能够满足使用要求。

浮动阀座-闸板密封结构的载荷边界条件见图7。 其中主要载荷包括介质压力、弹簧预紧力以及介质对浮动阀座的作用力。图7 中A 处为阀杆对闸板起限制作用，设为沿z 轴的固定约束；B处为上阀杆的下端面对闸板起限制作用，设为沿x 轴的固定约束；C、D 处设置为限制位移约束，确保闸阀全关时密封结构在x、y 轴方向不发生位移。

图7 浮动阀座-闸板密封结构载荷边界条件

介质压力pJ=5 MPa，弹簧预紧力FMT的计算公式为：

式中，N1为弹簧数量，个；L1为弹簧预加变形量，d为弹簧钢丝直径，R 为弹簧中径，mm；G 为弹簧弹性模量，MPa；S 为弹簧有效圈数。

介 质 作 用 力FMJ计 算 公 式 为［13］：

式中，R0为阀座活塞套筒外径，mm。

经过分析计算， 得到了浮动阀座-闸板密封结构的总变形云图、 等效应力云图以及接触应力云图，分别见图8～图10。

图8 浮动阀座-闸板密封结构总变形云图

图9 浮动阀座-闸板密封结构等效应力云图

图10 浮动阀座-闸板密封结构接触应力云图

分析图8～图10 可知，浮动阀座- 闸板密封结构的最大总变形为0.594 43 mm，最大等效应力为109.86 MPa，最大接触应力为25.343 MPa。 密封结构变形过大会使结构发生泄漏， 无法实现使用性能要求。 最大等效应力出现在浮动阀座密封面的边缘处且小于许用应力值， 但出现应力集中现象， 导致该密封结构发生早期失效的概率大为增加。因此，在优化过程中应有效降低该密封结构的等效应力。

此外， 浮动阀座- 闸板密封结构密封面上接触应力过大导致密封面磨损严重， 影响密封面的使 用 寿 命［14］。

3 浮动阀座-闸板密封结构参数敏感性及响应曲线分析

敏感性分析可得出各自变量参数对目标输出量的影响程度， 并针对性地对某自变量进行优化设计。根据研究技术指标、设计经验及结构参数特点，将D1、D2、R1、R2及R3变化范围设定为±10%。通过CCD 方法在数据样本空间中构造出27 个试验设计点，各设计点计算结果见表2。

表2 CCD 方法构造出的浮动阀座-闸板密封结构试验设计点及计算结果

浮动阀座- 闸板密封结构全局敏感性分析结果见图11。 根据图11 可知，自变量对输出量的影响各不相同。 5 个自变量对质量的影响均为正相关，其中D1对质量的敏感度最大。 5 个自变量对最大总变形、 最大接触应力以及最大等效应力的影响均呈负相关性，即增大自变量数值，输出量数值减小。R2对最大总变形的敏感度最高。R2和D2对最大等效应力和最大接触应力的敏感度最高，此时增大自变量可降低输出量的数值， 这是浮动阀座结构参数优化时需考虑的主要方面。

图11 浮动阀座-闸板密封结构全局敏感性分析结果

浮动阀座-闸板密封结构局部敏感性分析结果见图12，通过该结果可快速查看各尺寸参数对最大等效应力和最大接触应力的敏感趋势。 从图12 可以看出， 每条敏感性曲线都交于响应点，在该点处各自变量对最大等效应力的敏感度均一致。

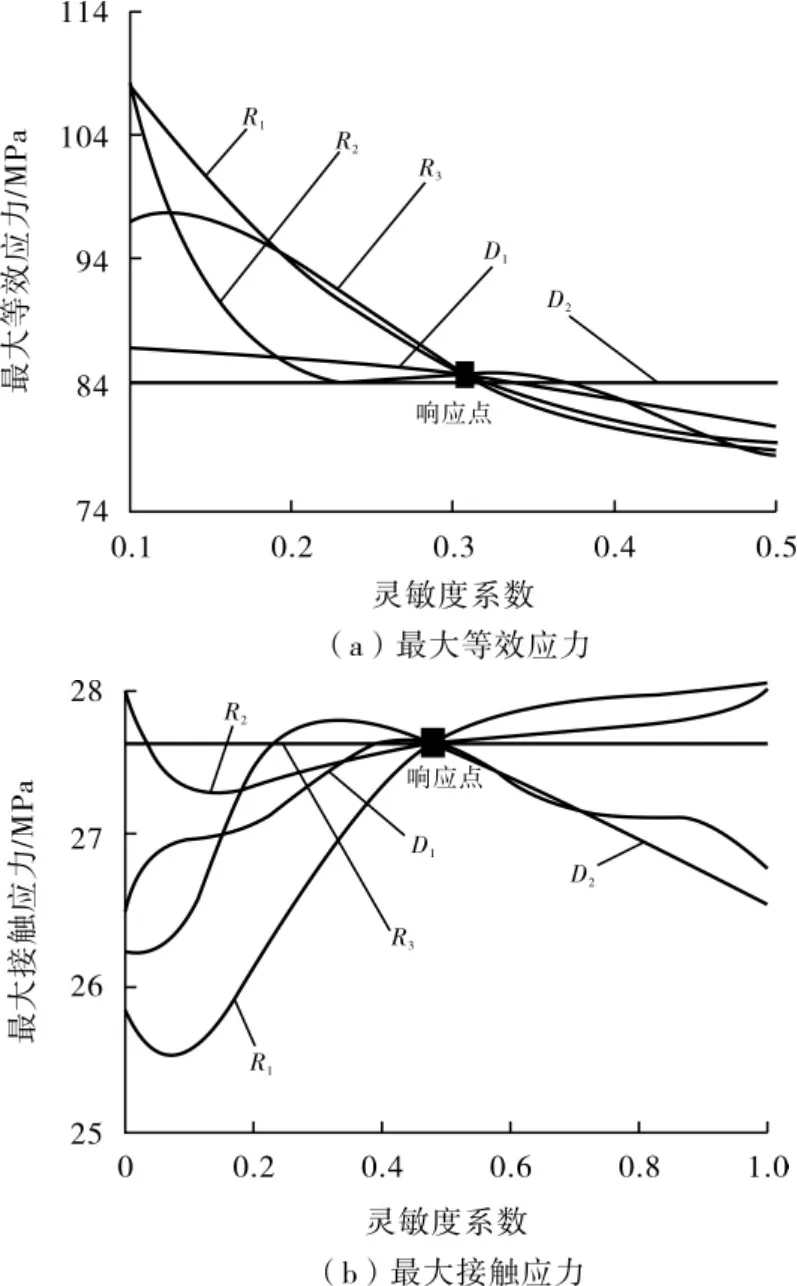
图12 浮动阀座-闸板密封结构局部敏感性分析结果

Response Surface Optimization 模块利用全二阶多项式拟合出响应面函数［15］。 浮动阀座-闸板密封结构拟合度评价结果见表3， 说明拟合出的响应曲线结果可信。

表3 浮动阀座-闸板密封结构拟合度评价结果

综合考虑浮动阀座-闸板密封结构的全局和局部敏感性分析结果， 需要重点关注D2和R2对最大接触应力和最大等效应力的响应曲线。 根据式（1），利用最小二乘法求解式中多项式系数，得到了浮动阀座-闸板密封结构最大接触应力和最大等效应力随R2和D2变化的响应曲线， 分别见图13、图14。

图13 浮动阀座-闸板密封结构最大应力随密封面中径响应曲线

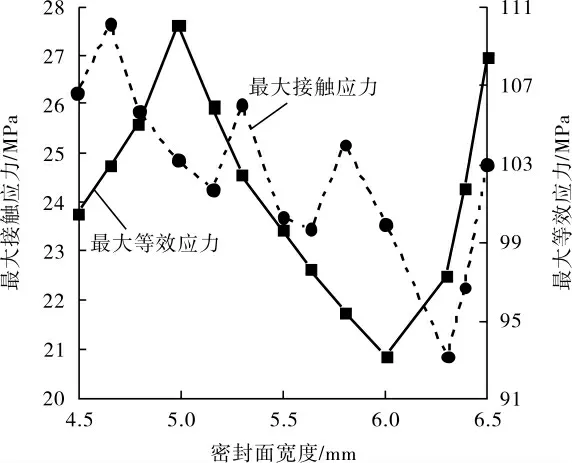
图14 浮动阀座-闸板密封结构最大应力随密封面宽度响应曲线

由图13 可知， ①随着R2的增大， 在156～160 mm、160～163 mm 和163～166 mm 区间， 密封结构的最大接触应力均呈现先升高后降低的趋势。②随着R2的增大，在156～164 mm 区间，密封结构最大等效应力出现先升高后降低的趋势，在局部出现极值。

由图14 可知， ①随着D2的增大， 在4.5～5.25 mm、5.25～5.75 mm 和5.75～6.25 mm 这几个区间， 密封面的最大接触应力均呈现先升高后降低的趋势，且在局部出现极值。 ②随着D2的增大，在4.5～6 mm 区间，密封结构的最大等效应力出现先升高后降低的趋势，且在局部出现极值。最大应力变化规律可以为密封结构的优化设计提供参考。

4 浮动阀座结构参数多目标优化分析

结构参数优化设计往往涉及多目标优化，目标间可能存在矛盾，例如，浮动阀座厚度增大，最大整体变形量减小，但密封结构体积增大，导致密封结构质量增加。因此，在多目标优化时应寻找最优平衡点[16]。

对于浮动阀座- 闸板密封结构， 应寻找一组最优组合的结构参数， 在满足其密封性能的基础上，尽可能减小质量，降低接触应力并减小应力集中，即：

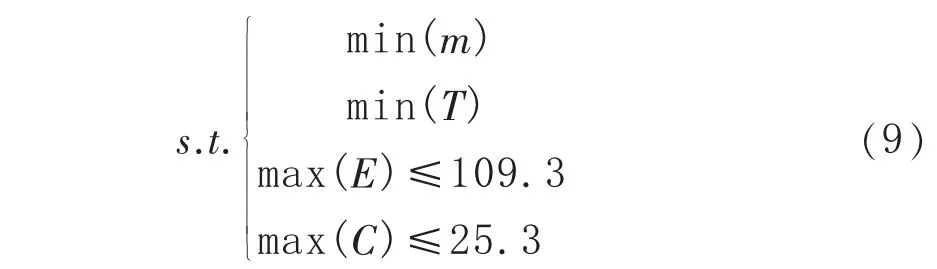
式中，m 为密封结构质量，kg；T 为密封结构最大总变形，mm；E 为密封结构最大等效应力，C 为密封结构最大接触应力，MPa。

利用Response Surface Optimization 模块对浮动阀座结构参数进行约束赋值， 通过与目标期望值的不断比较， 得到了3 组优化方案，见表4。

表4 浮动阀座-闸板密封结构优化设计方案

根据前述分析， 求解过程中需主要关注最大等效应力和最大接触应力值， 因此选择数值最小的优化方案3。 优化后密封结构的最大等效应力为84.1 MPa， 比原密封结构降低23.5%； 优化后密封结构的最大接触应力为20.3 MPa，比原结构降低19.2%； 优化后密封结构的质量为19.1 kg，比原结构降低9.5%。

根据选取的最优解集，得到介质压力pJ（pJ∈[3，10]） 与D1、D2和R2之 间 的 关 系 式， 即 式（10）。 根据式（10），已知任一参数，便可实现此类密封结构参数的快速且高效的设计。

5 结语

浮动阀座- 闸板密封结构失效的根本原因是浮动阀座的主要设计参数不合理， 导致密封面接触应力过大以及出现等效应力集中现象。 通过对该密封结构进行灵敏度分析和响应面法分析，得到了主要结构参数对密封结构密封性能的影响规律。优化后浮动阀座-闸板密封结构的最大等效应力、最大接触应力及质量均不同程度减小，达到了降低浮动阀座-闸板密封结构的应力集中、减轻密封结构质量以及延长密封结构使用寿命的目的。文中得到的与介质压力有关的主要结构参数设计方法， 能够为其他同类型阀门密封结构的快速及高效设计提供理论基础。