地震作用下斜坡桩土相互作用关系研究
李久栋
(中铁十九局集团第三工程有限公司 辽宁沈阳 110036)
1 引言
在地震荷载作用下,斜坡易发生失稳破坏,通过桩基对坡体进行处理是常见的加固手段,桩基在地震荷载作用下的动力响应规律一直是相关领域研究的重点[1-4]。
刘爱娟等[5]基于蒙特卡洛理论,提出了一种模拟地震临界加速度动态变化的方法,对传统的地震稳定性评价方法进行了优化。乔蓓等[6]基于强度折减法,对地震作用下的边坡稳定性问题进行了分析。王来贵等[7]研究了地震作用下边坡摩擦效应和滑动机理,揭示了边坡结构面法向应力变化规律。刘爱娟等[8]考虑到边坡土体材料的不均匀性,将不均匀性应用到地震边坡永久位移的计算方法中。宋波等[9]通过振动台试验,研究了不同桩基形式在地震荷载作用下的动力响应规律。罗川等[10]建立了三维有限元桩基模型,研究了桩-土相互作用对地震响应规律的影响。
为研究地震作用下斜坡桩基的动力响应规律,本文基于土体多屈服面模型和桩-土动力弹簧模型建立了斜坡段群桩有限元模型,通过离心机振动台在5种不同地震峰值加速度工况下进行了桩基动力响应试验,利用试验结果与数值计算结果进行了对比,验证了模型的有效性。基于此,对斜坡坡角和桩身直径对桩基动力响应的影响进行了探究。
2 桩-土本构模型
2.1 多屈服面模型
动力作用下的土体可以通过多屈服面模型进行模拟,在地震荷载作用下,多屈服面模型能较好地反映应力路径和土体应力影响现象。Yang等[11]构建了基于围压多屈服面Pressure Dependent Multi-Yield(PDMY)模型,可以在循环荷载作用下有效模拟土体非线性变形,在反映应力应变循环滞回现象中也有较好的表现。
在弹性阶段,PDMY模型基于各向同性假定;在塑性阶段,则考虑土体的各向异性。图1展示了屈服面的空间形式。如图1所示,在主应力空间中,屈服面以圆锥面的形式展现,硬化区由共顶点的圆锥面共同形成,而破坏面则被定义为最外围的圆锥表面。
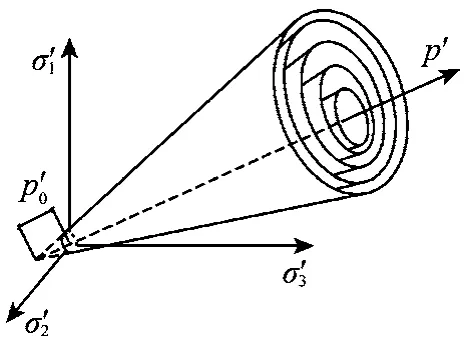
图1 主应力空间中的多圆锥屈服面
2.2 桩-土动力弹簧模型
参考相关研究[12]并结合工程实际,如图2所示,通过动力弹簧组合来模拟桩-土之间的相互作用。在土体和桩同一位置处,通过离散化插入非线性单元来模拟桩基的动力特性。动力弹簧有三种类型,分别用来模拟沿桩身垂直方向上土体抗力的p-y弹簧,模拟桩身外表面桩侧摩阻力的t-z弹簧,以及用来模拟桩端土体承载力的Q-z弹簧。
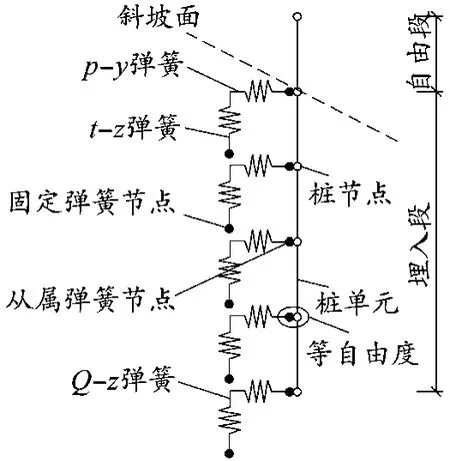
图2 土-桩相互作用模型
3 数值计算模型验证
图3为通过二维有限元软件建立的斜坡段群桩有限元模型示意图。其中,斜坡坡度设为26°,坡体由上层的砂土和下层的基岩两种土体构成,上层砂土的厚度为10.5 m,基岩层厚度在水平段为14.5 m。有限元模型中的桩长28 m,桩距2.5 m。依据相关文献和实际工程经验,砂土通过PDMY模型模拟,桩和基岩模型选用线弹性模型,表1为砂土的模型输入参数,表2为基岩和桩的模型输入参数。

表1 砂土模型输入参数

表2 基岩和桩基模型输入参数
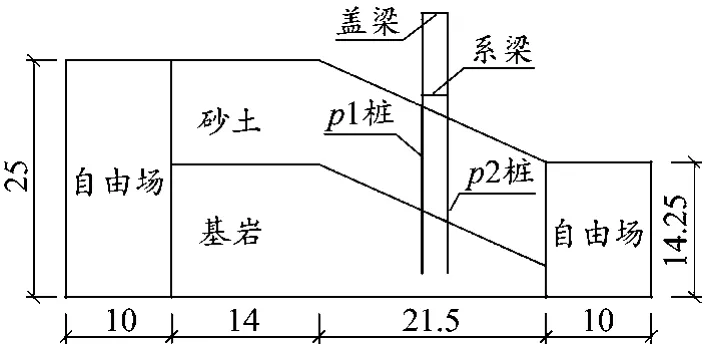
图3 二维有限元模型(单位:m)
模型边界条件设置为底部固定边界,水平向边界基于半无限空间体理论,采用L-K粘性边界,模型顶部边界条件为自由。为在保证计算精度的前提下,兼顾计算效率,划分网格时对砂土和基岩截面以及桩基周围进行局部网格加密处理,共划分出34 132个10节点有限元网格。
为了验证模型的有效性,本文进行了离心机振动台试验。通过在模型箱底部设置形式为EL-Centro波的地震波来模拟地震作用,设置5种不同的地震波峰值加速度,分别为 0.148 2 g、0.211 2 g、0.304 8 g、0.428 9 g和0.481 2 g,通过5种不同地震波峰值加速度下的桩身动力响应实测值与模拟值进行对比,来进行斜坡段群桩有限元模型的验证。
图4和图5展示了试验和数值计算结果对比情况。图4为不同地震加速度工况下桩体残余水平位移随测点到桩底距离变化情况,图5为不同地震加速度工况下埋入段桩身最终弯矩随桩体埋深的变化情况。从图4和图5可以看出,在5种地震加速度作用下,数值计算结果与试验结果数值和变化趋势均较为一致,这说明斜坡段群桩有限元模型在本构模型选择、网格划分、参数选取和边界条件设定等方面较为合理、正确。
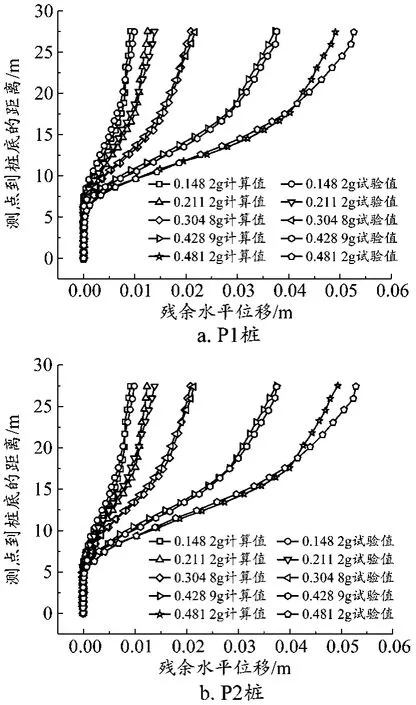
图4 不同工况下桩身残余水平位移
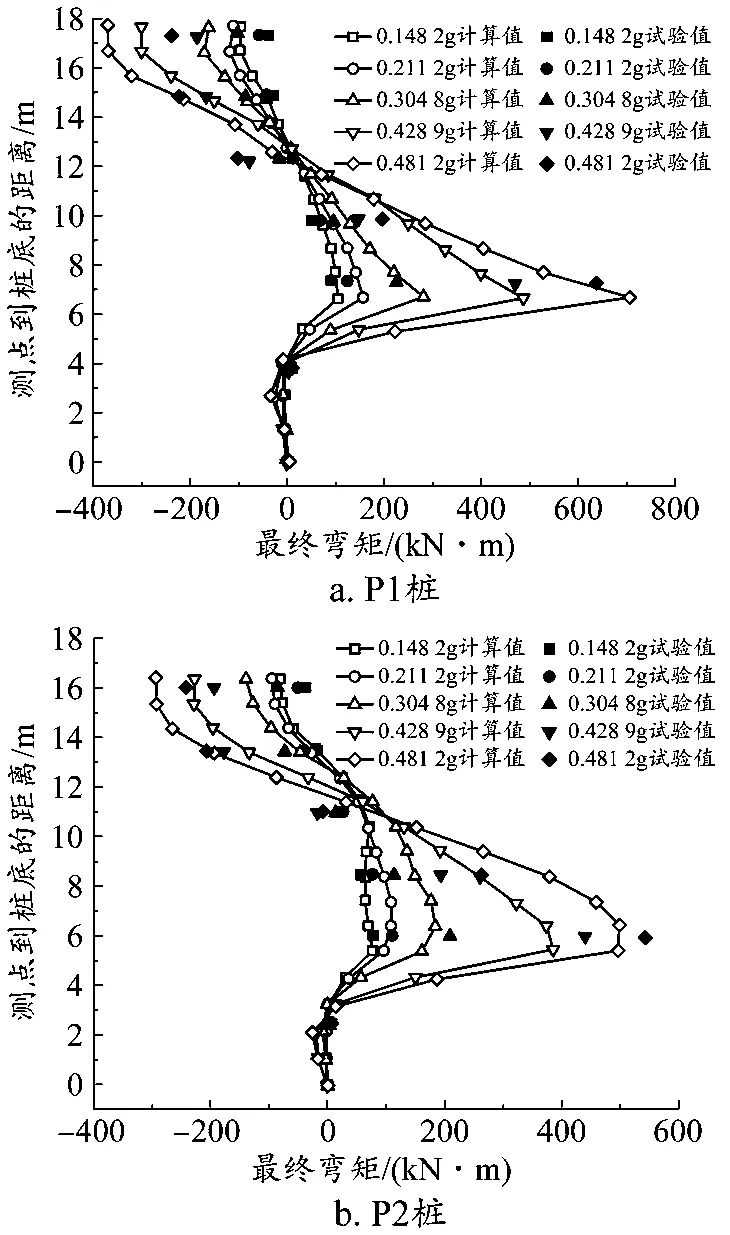
图5 不同工况下埋入段桩身最终弯矩
从图4中可以看出,在不同加速度作用下P1桩和P2桩的残余水平位移随测点到桩底的距离变化较大,同一测点到桩底距离情况下,出现了地震加速度越高桩体残余水平位移越大的一般性规律,随着加速度的增大,桩身残余水平位移增加。同一地震加速度工况下,随着测点到桩底距离的增加,残余水平位移增大,桩身残余水平位移与到桩底距离呈正相关关系。对比P1桩与P2桩,如图4a和图4b所示,两个桩体间的残余水平位移未表现出明显差异。
图5展示了不同工况下埋入段桩身最终弯矩。从图中可以看出,在基岩与砂土交界面,最终弯矩出现明显增大,这可能是由于两种土体性质不同,出现了应力集中现象,导致附近的桩体弯矩增大。桩体上部弯矩为负,桩体中下部弯矩为正。同一桩体高度下,随着地震加速度的增大,桩体的最终弯矩数值提高,弯矩变化幅值也增大。对比图5a和图5b,两种桩体之间的最终弯矩出现了较为明显的差异情况,同一地震加速度下,桩体位置相同时P1桩最终弯矩的数值较大,变化幅度也高于P2。这是由于P1桩为后排抗滑桩,在地震作用下,边坡高度较高处更易发生变形,P1直接承受了更大的边坡土体推力作用,因而表现出了较大的桩体弯矩。
4 影响因素分析
为了进一步分析地震作用下的桩基动力响应,选取斜坡坡角和桩身直径作为变量进行分析。该数值试验是在地震加速度0.481 2 g条件下进行,根据以上研究,P1桩和P2桩在残余水平位移方面未表现出明显差异,因此本次分析从P1桩的残余水平位移、最终弯矩和P2桩的最终弯矩随桩体深度变化情况进行。
4.1 斜坡坡角
图6展示了不同斜坡坡脚工况下的桩身动力响应,图6a为P1桩的残余水平位移曲线,图6b为P1桩的最终弯矩曲线,图6c为P2桩的最终弯矩曲线。从图6a中可以看出,同一测点到桩底距离下,随着斜坡坡角的增大,桩体的残余水平位移增加,桩体残余水平位移与斜坡坡角呈正相关关系。在桩身中段,残余水平位移随测点到桩底距离的增加,增大速率较快,后速率逐渐降低,最后趋于平缓。从图6b和图6c中可以看出,同一测点到桩底距离下,随着斜坡坡角的增大,桩体最终弯矩数值增加,且其随测点到桩底距离变化曲线幅度也越大。可见,斜坡坡角的增大不利于斜坡的稳定,较陡的斜坡更容易出现失稳情况的发生。此外,对比图6b和图6c,P1桩在不同斜坡坡角工况下的最终弯矩数值和变化幅度均大于P2桩,这说明在地震荷载作用下后排抗滑桩承受了更大的斜坡土体作用,因此,在实际工程中应更注重后排抗滑桩的承载性能。
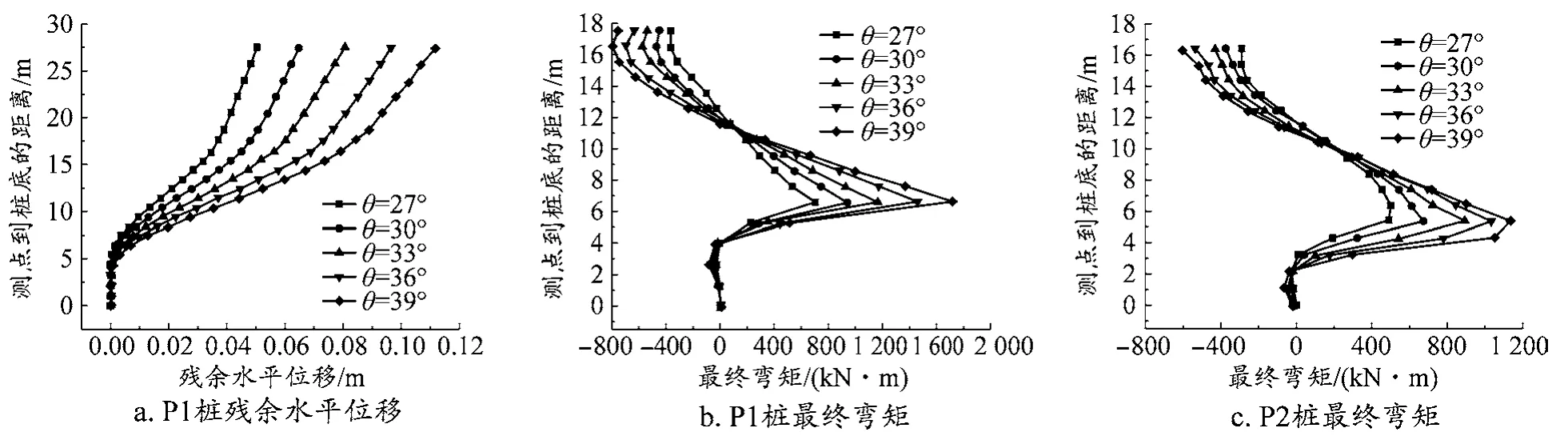
图6 不同斜坡坡脚工况下的桩身动力响应
4.2 桩身直径
图7展示了不同桩径工况下的桩身动力响应,图7a为P1桩的残余水平位移曲线,图7b为P1桩的最终弯矩曲线,图7c为P2桩的最终弯矩曲线。从图7a中可以看出,同一测点到桩底距离下,随着桩身直径的增加,桩体残余水平位移减少,桩身直径与桩体残余水平呈负相关关系。从图7b和图7c中可以看出,同一测点到桩底距离下,随着桩身直径的增加,桩体最终弯矩数值增大,但除了在基岩与砂土交界面和桩顶位置处,其他位置处各工况下的差异并不显著。这是由于,增大桩身直径,会提高桩体承载能力和自身刚度,增加了对斜坡土体的抵抗性能,减小了变形,因此桩体会出现较大的内力。对比图7b和图7c,增加桩身直径对桩体最终弯矩的影响效果P2桩体要大于P1桩体,且在坡面位置处,与基岩与砂土交界面的规律相反,P2桩直径越大,最终弯矩值越小。
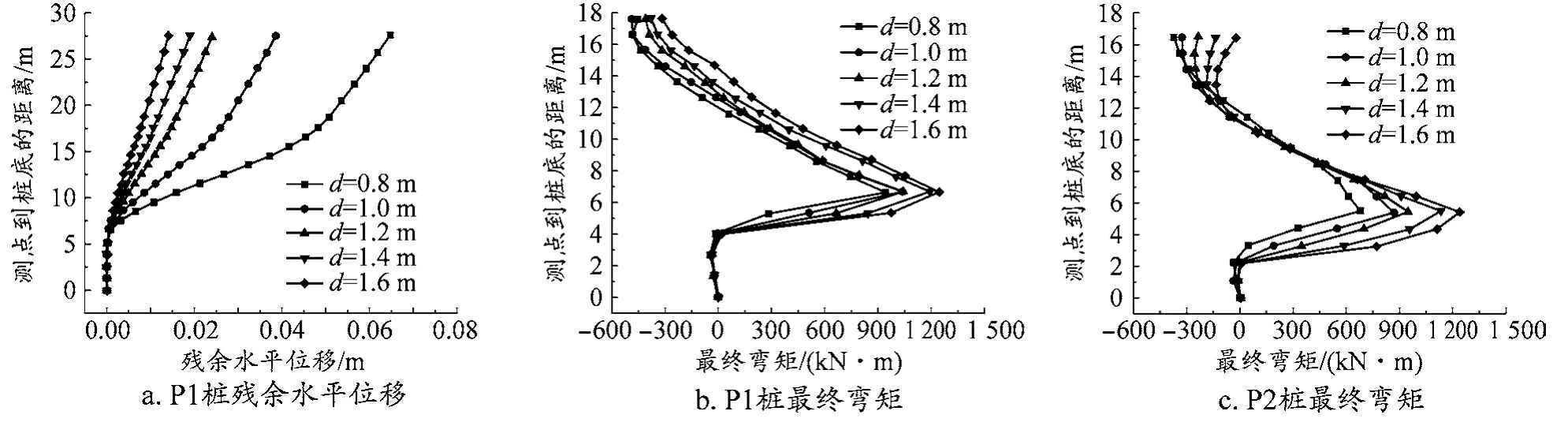
图7 不同桩径工况下的桩身动力响应
5 结论
基于土体多屈服面模型和桩-土动力弹簧模型建立了斜坡段群桩有限元模型,通过离心机振动台试验在5种不同地震峰值加速度工况下进行了桩基动力响应试验,利用试验结果与数值计算结果进行了对比,验证了模型的有效性。基于此,对斜坡坡角和桩身直径对桩基动力响应的影响进行了探究,得出主要结论如下:
(1)在5种地震加速度作用下,数值计算结果与试验结果数值和变化趋势均较为一致,这说明斜坡段群桩有限元模型在本构模型选择、网格划分、参数选取和边界条件设定等方面较为合理、正确。
(2)同一测点到桩底距离情况下,出现了地震加速度越高桩体残余水平位移越大的一般性规律;同一地震加速度工况下,随着测点到桩底距离的增加,残余水平位移增大,桩身残余水平位移与到桩底距离呈正相关关系。
(3)桩体上部弯矩为负,桩体中下部弯矩为正,在基岩与砂土交界面,最终弯矩出现明显增大。同一桩体高度下,随着地震加速度的增大,桩体的最终弯矩数值提高,弯矩变化幅值也增大。
(4)随着斜坡坡角的增大,桩体的残余水平位移和最终弯矩均有所提高。增大桩径,能提高桩体刚度,减小桩体变形,但增加了自身内力。

