池黄高铁三塔矮塔斜拉桥施工控制参数研究

王 强 陆小雨

(1.皖赣铁路安徽有限责任公司 安徽合肥 230000；2.中铁上海设计院集团有限公司 上海 200070)

1 引言

矮塔斜拉桥以其桥塔高度低、主梁高度高的特点与常规斜拉桥区别开来，主梁为主要受力构件，拉索可视为体外预应力束对主梁进行加劲，因此学界又称其为部分斜拉桥[1]。随着中国铁路网的快速建设，这一桥型在主跨150～300 m的桥式方案中具有较大的竞争力，受到了桥梁设计师的普遍青睐[2]。

由于实际施工过程与设计假定的施工步骤和荷载会有所差别，这就需要在施工过程中，通过施工控制对结构参数误差进行修正，让桥梁尽量能达到设计的合理成桥状态[3]。为实现这一目标，需要对可能导致桥梁偏离设计理想状态的各类因素进行研究，分析成桥状态下结构内力和变形对各类参数的敏感性[4]。

随着矮塔斜拉桥在近年来的推广应用，双塔矮塔斜拉桥的施工控制已有较多的研究成果，而针对多塔矮塔斜拉桥的研究还不够充分[5]。因此，有必要针对多塔矮塔斜拉桥的施工控制进行研究。

本文以新建池黄高铁三塔六跨矮塔斜拉桥为工程背景，选取主梁自重、主梁刚度、拉索初张拉力、拉索二次张拉次序、合龙温度等参数，计算分析以上参数对桥梁力学性能的影响，为施工控制提供可靠的技术依据，为保证最终能达到合理成桥状态提供有效的支撑[6]。

2 工程背景

池黄高铁太平湖特大桥主桥为三塔六跨矮塔斜拉桥，结构体系为边塔梁固结—中塔刚构的组合体系[7]，主桥长度为789.7 m(含支座中心线到梁端0.85 m)，桥跨布置为(48＋118＋2×228＋118＋48)m。主梁采用单箱双室直腹板截面，梁高为6.0～12.0 m。桥塔采用双柱式矩形截面，有效塔高均为35 m，单个桥塔设9对斜拉索。

主桥桥型布置如图1所示，桥跨编号从小里程到大里程依次为A跨～F跨，桥墩位置分别为③号墩～⑨号墩，拉索编号分别为 A9→A1、B1→B9、C9→C1、C1→C9、B9→B1、A1→A9。

图1 桥型布置(单位:m)

3 有限元模型的建立

采用有限元分析软件Midas Civil 2021建立斜拉桥的计算模型，全桥共划分为937个节点，889个单元。其中，塔、梁、墩台和桩基均采用梁单元模拟，拉索采用桁架单元模拟，桩基底部采用固结约束，其他桥墩采用节点支承进行模拟。

0号块和边跨现浇段采用支架现浇法施工，其余梁段采用挂篮悬臂浇筑，施工过程共划分为57个施工阶段，其中悬臂梁段的施工内容主要包括挂篮移动、梁段浇筑、预应力筋的安装与张拉、斜拉索的安装与张拉。桥梁有限元模型如图2所示。

图2 桥梁空间有限元模型

4 施工控制参数研究

4.1 研究方法

根据施工经验，选取主梁自重、主梁刚度、拉索初张拉力、拉索二次张拉次序和合龙温度五个参数进行研究，以设计参数作为基准状态，通过改变某个参数的取值，同时保持其余参数不变，对桥梁的力学性能进行分析。由于矮塔斜拉桥的竖向刚度主要由主梁和拉索提供，桥塔的作用仅为提供斜拉索的转向[8]，因此选取成桥状态下主梁线形、主梁应力、拉索内力为施工控制的重要目标，最后对各参数对控制目标的影响程度进行排序[9]，见表1。

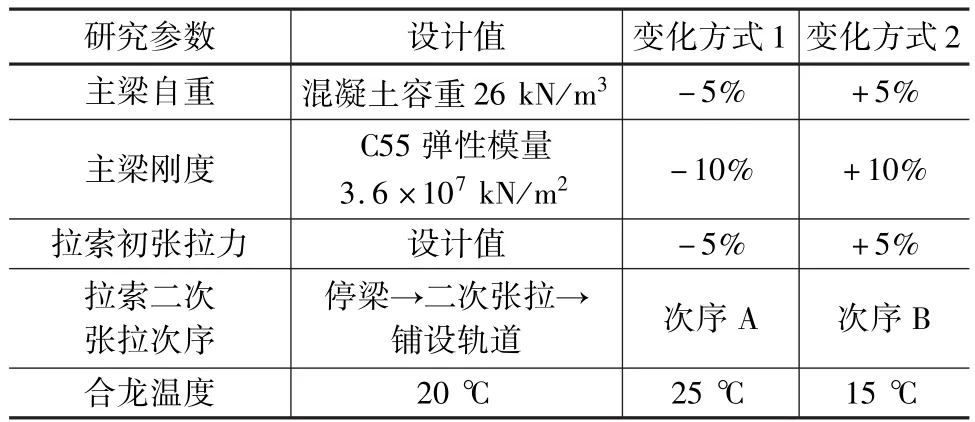
表1 主要研究参数及变化方式

4.2 主梁自重

由于施工现场的混凝土容重与设计采用值不可能完全一致，故通过改变主梁混凝土容重实现主梁自重的变化。以主梁混凝土容重设计值为基准状态，按幅度为±5%对混凝土容重进行变化，计算分析成桥状态下主梁线形、主梁上下缘应力和拉索内力的变化值，计算结果如图3所示。图中横坐标表示主梁顺桥向的位置，起点为边支点，由于本桥为对称结构，故图中仅示半桥的结果，下同。

由图3可知，当主梁自重变化5%时，主梁竖向下挠值最大增加15.4 mm；主梁上、下缘压应力最大增加值分别为1.1 MPa和1.07 MPa，对应增幅分别为8.9%和14.7%；拉索内力最大增加26.5 kN，增幅为0.3%。主梁自重变化对3/8跨处竖向挠度和中支点主梁上、下缘应力影响最大；长索受到主梁自重变化的影响相比短索要大。

综上所述，主梁自重变化对桥梁的力学性能影响不可忽略，由于高铁行车对主梁线形较为敏感[10]，因此在施工过程中，需根据现场混凝土的实际容重对计算模型进行修改，对主梁预拱度值进行修正，保证桥梁能达到设计成桥线形。

4.3 主梁刚度

由于现场的混凝土弹性模量与设计值不可能完全一致，故主梁刚度的变化通过改变混凝土弹性模量来实现[11]。以主梁C55混凝土弹模设计值为基准，按幅度为±10%对混凝土弹模进行变化，保持其他参数不变，计算结果如图4所示。

图4 主梁刚度误差对结构内力、变形的影响规律

由图4可知，主梁弹性模量变化10%，主梁竖向挠度最大增加7.8 mm；主梁上、下缘压应力最大增加值均为0.1 MPa，增幅分别为0.9%和1.0%；成桥拉索内力最大增加21.7 kN，增幅为0.4%。

因此，主梁刚度变化对成桥状态的线形影响较大，而对主梁应力和拉索内力的影响可忽略不计。由于高速铁路对桥梁线形要求高，因此在施工过程中仍需保证混凝土弹性模量与设计值尽量一致，若有差别时，应及时调整计算模型，对预拱度进行修正。

4.4 拉索初张拉力

根据施工经验，斜拉索在张拉后，其内力很难与设计值完全一致[12]，以拉索初张拉力的设计值为基准，按幅度为±5%对其进行变化，计算结果如图5所示。

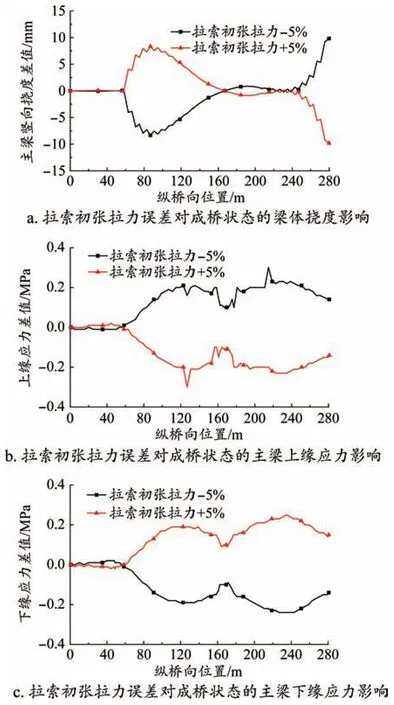
图5 拉索初张拉力误差对结构内力、变形的影响规律

由图5可知，拉索初张拉力变化5%，主梁竖向挠度最大增加10.12 mm；主梁上、下缘压应力最大增加值分别为0.23 MPa和0.24 MPa，增幅分别为2.8%和3.1%；成桥拉索内力最大增加70.9 kN，增幅为1.0%。

因此，拉索初张拉力变化对成桥状态的线形影响较大，对主梁应力和拉索内力的影响较小。由于斜拉索在铺轨前会进行拉索的二次张拉，因此初张拉力变化时，成桥阶段的拉索内力变化很小。

4.5 拉索二次张拉次序

设计指定的施工次序为:停梁60 d→斜拉索二次张拉→铺设轨道。以此为基准状态，考虑以下2种张拉次序:(1)次序A，拉索二次张拉→停梁60 d→铺设轨道；(2)次序B，停梁60 d→铺设轨道→拉索二次张拉。计算结果如图6所示。

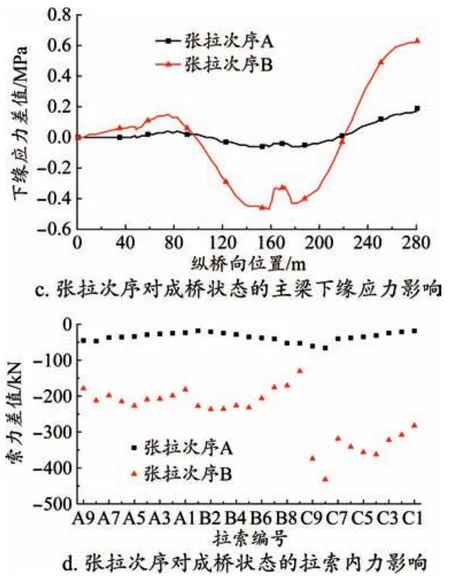
图6 张拉次序对结构内力、变形的影响规律

由图6可知，张拉次序A相比于张拉次序B对结构的内力和变形影响较小。当采用张拉次序B时，主梁竖向挠度最大下挠39.0 mm；主梁上、下缘压应力最大增加0.6 MPa和0.47 MPa，增幅分别为9.5%和8.2%；成桥拉索内力最大增加432.0 kN，增幅为5.8%。

因此，采用张拉次序B对施工控制重要目标的影响均较大，因此实际施工时，二次张拉应按设计指定次序进行，以确保桥梁达到理想成桥状态。

4.6 合龙温度

设计时假定合龙温度为20℃，由于实际工期未必能满足设计要求，本文按幅度为±5℃对合龙温度进行变化，计算结果如图7所示。

图7 合龙温度对结构内力、变形的影响规律

由图7可知，合龙温度变化5℃时，主梁竖向挠度最大增加1.6 mm，主梁上缘压应力最大增加0.04 MPa，增幅为0.6%；主梁下缘压应力最大增加0.05 MPa，增幅为0.5%；成桥索力最大增加21.0 kN，增幅为0.3%。

综上可知，合龙温度变化对施工控制的重要目标结果影响均较小。由于结构采用了边塔梁固结—中塔刚构的组合体系，使得结构对温度的敏感性相比于全刚构体系大大降低[13]。

4.7 小结

(1)主梁线形敏感性参数研究

对影响主梁线形的各个参数的敏感性进行排序，如表2所示。表中参数对施工控制重要指标的影响越大，其编号越小，下同。

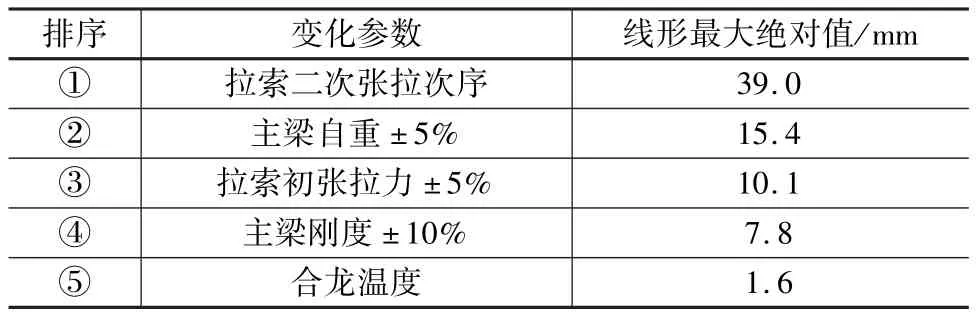
表2 主梁线形敏感性参数研究结果汇总

由表2可知，拉索二次张拉次序、主梁自重、拉索初张拉力和主梁刚度是主梁线形的主要敏感性参数，合龙温度为次要敏感性参数。

(2)主梁应力敏感性参数研究

对影响主梁应力的各个参数的敏感性进行排序，如表3所示。

表3 主梁应力敏感性参数研究结果汇总

由表3可知，主梁自重、拉索二次张拉次序是主梁应力的主要敏感性参数，其余均为次要敏感性参数。

(3)拉索内力敏感性参数研究

对影响拉索内力的各个参数的敏感性进行排序，如表4所示。

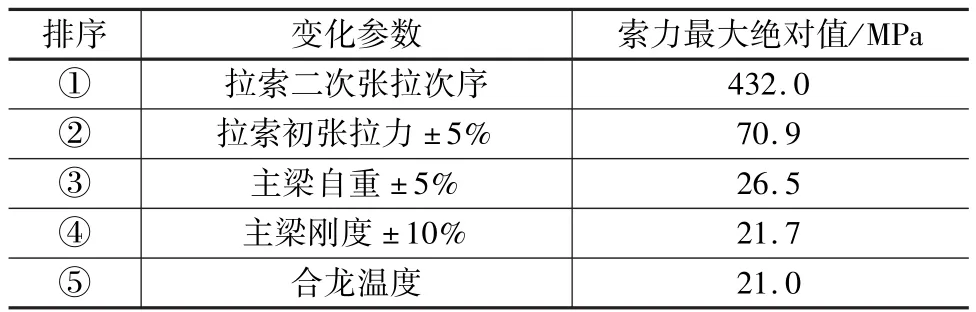
表4 拉索内力参数敏感性参数研究结果汇总

由表4可知，拉索二次张拉次序和拉索初张拉力是拉索内力的主要敏感性因素，其他因素的变化对主梁线形影响很小。

5 结语

本文对池黄高铁(48＋118＋2×228＋118＋48)m多塔矮塔斜拉桥的施工控制参数进行研究，得出结论如下:

(1)由于高速铁路行车对主梁线形较为敏感，主梁自重和刚度、拉索初张拉力和二次张拉次序对主梁线形影响均较大，施工过程中应对以上参数进行严格控制，以保证桥梁能达到设计线形。

(2)主梁应力受主梁自重的变化影响较大，由于矮塔斜拉桥以主梁受力为主，主梁内力较大，因此需严格控制主梁自重这一参数以保证主梁内力能达到设计指定状态。

(3)拉索二次张拉次序和拉索初张拉力是拉索内力的主要敏感性参数，施工过程中应对张拉后的拉索索力进行复测，对索力偏差较大的拉索应及时调整，确保索力与设计值一致。

(4)本桥采用边塔梁固结—中塔刚构的组合体系，该体系对温度的敏感性较低，在季节温度变化结构的受力性能变化较小。