基于改进DQN算法的NPC行进路线规划研究

刘 森，李 玺，黄 运

(1.河北远东通信系统工程有限公司， 河北 石家庄 050200；2.陆军工程大学石家庄校区，河北 石家庄 050000;3.中国人民解放军32620部队，青海 西宁 810007)

0 引言

在军事游戏或仿真训练系统中，非玩家角色(No-player Character,NPC)的智能化水平在很大程度上决定了模拟训练的效果。构建NPC的核心是进行行为建模。行为建模分为认知行为建模和物理行为建模，行进路线的规划则是NPC物理行为建模的重要组成部分。传统的NPC行进路线规划主要采用固定路线或利用有限状态机、行为树构建脚本等方式。前者相对比较原始，很难有效提升模拟训练的效果，后者具有一定的智能性，但是面对复杂多变的战场环境往往不能灵活应对。本文针对上述问题开展研究，利用强化学习(Reinforcement Learning,RL)的方法设计NPC行进路线规划算法，实现NPC行进路线的智能化选择。

近年来，深度学习(Deep Learning,DL)和RL相结合产生的深度强化学习(Deep Reinforcement Learning,DRL)，使传统的RL扩展到高维度状态空间和高维度动作空间等以前无法解决的领域[1]。特别是Mnih等人[2]提出的深度Q网络(Deep Q-Network,DQN)将DRL的研究推向新的高度。目前，各国学者利用DRL在机器人控制[3-4]、游戏[5]和无人驾驶[6-7]等领域开展了广泛而深入的研究。其中,基于DRL的路线规划研究[8-14]也是热点之一，同时也是多领域的基础应用研究内容。

上述研究多关注于如何进行避障，而在此基础上如何实现最优路线的选择研究较少。另外，由于DQN算法在经验回放时采用均匀的采样方法，不利于算法的收敛。本文针对DQN算法收敛性差和最优路线选取问题进行改进，提出PRDQN算法。该算法利用基于SumTree的优先经验回放方法取代了DQN算法的均匀采样回放机制，并重新设计了奖励函数。实验证明，该算法相对于DQN算法不仅提高了收敛速度，而且实现了路线的优化。

1 PRDQN算法

1.1 Q-learning算法

Q-learning是RL的经典算法，核心是智能体通过与环境的不断交互学习，更新和完善Q-table，以达到智能决策的目的。Q-table的行代表状态，列代表行动，表格的数值即Q-value是在不同状态下采取相应行动时能够获得的最大的未来期望奖励。Q-learning算法利用式(1)来计算Q-value:

Q(st,at)=Q(st,at)+

α[rt+γmaxQ(st+1,at+1)-Q(st,at)]。

(1)

式(1)展开可得：

Q(st,at)=(1-α)Q(st,at)+

α[rt+γmaxQ(st+1,at+1)]。

(2)

将式(2)进行迭代，得：

Q(st,at)=(1-α)Q(st,at)+α[rt+γmaxQ(st+1,at+1)]=

(1-α){(1-α)Q(st,at)+

α[rt+γmaxQ(st+1,at+1)]}+

α[rt+γmaxQ(st+1,at+1)]=

(1-α)2Q(st,at)+

[1-(1-α)2][rt+γmaxQ(st+1,at+1)]=

…=

(1-α)nQ(st,at)+

[1-(1-α)n][rt+γmaxQ(st+1,at+1)],

(3)

式中，st为t时刻的状态；at为t时刻采取的行动；st+1为t+1时刻的状态；at+1为t+1时刻采取的动作；Q(st,at)为st状态下采用行动at的值函数；α为学习率；rt为t时刻已经获得的奖励；γ为衰减因子。由于α∈(0,1)，因此0<α-1<1，当n→∞时，(1-α)n→0，则式(3)可变为：

Q(st,at)=rt+γmaxQ(st+1,at+1)。

(4)

式(4)即是在各类程序中，计算st状态下采用行动at的Q值公式。

利用Q-learning算法实现RL简单明了，并且不存在收敛性的问题。但是，当状态空间S和行动空间A足够大时，Q-table会变得非常大，从而导致维数灾难。因此，纯粹的Q-learning算法很少用于解决现实中的各类应用问题。

1.2 DQN算法

针对Q-learning算法存在的维数灾难问题，DeepMind团队的Mnih等人将深度卷积神经网络和Q-learning结合，利用卷积神经网络动态生成Q-table，不仅避免了复杂空间的维数灾难，而且在一定程度上解决了非线性函数近似表示值函数的不稳定问题。

DQN算法示意如图1所示，算法定义了2个相对独立且结构相同的网络，分别是训练网络(TrainingNet)和目标网络(TargetNet)。利用Q-learning算法，智能体通过与环境的交互，实现训练网络的学习。经过固定步数的训练后，将训练网络中的参数全部赋值给目标网络。设置经验回放单元的目的是减少训练样本的相关行，改善神经网络逼近强化学习的动作值函数不稳定的问题。每次训练时从经验库中均匀选取一批样本与训练样本混合在一起，破坏相邻训练样本的相关性，提高样本的利用率。

图1 DQN算法示意Fig.1 Schematic diagram of DQN algorithm

DQN的损失函数是目标网络的Q-value与评估网络的Q-value差的平方值，表示为：

LOSSt=(targetQt-Q(st,at,wt))2，

(5)

式中，targetQ根据式(4)可得：

targetQt=rt+γmaxQ′(st+1,at+1,wt+1)，

(6)

w为网络参数，采用梯度下降法学习：

wt+1=wt+E[targetQt-Q(st,at,wt)]Q(st,at,wt)。

(7)

1.3 改进算法

传统的DQN算法利用经验回放机制，阻断了训练样本的相关行，改善了不稳定的问题，但是采用均匀采样的方式不利于算法的收敛。另外，DQN算法奖励函数设置的比较简单，往往不能实现最优路线的规划。本文针对经验回放和奖励函数进行了改进，提出了PRDQN算法。

1.3.1 基于SumTree的优先经验回放

SumTree采用二叉树结构，如图2所示。节点存储的是样本的优先级(Priority)，数值越大，优先级越高，通过这种方式可以让好的样本重复利用的几率更大。SumTree中，只有叶子节点代表具体样本，非叶子节点没有实际意义，父节点的优先级是子节点优先级的和。叶子节点的优先级通过TD-error[15-17]确定，TD-error是样本在利用时序差分(Temporal Difference,TD)更新时目标网络值函数与训练网络值函数的差值，本文TD-error的值采用损失函数值，如式(5)所示。差值越大说明预测精度还有较大的上升空间，被训练的价值就越大，因此优先级越高。叶子节点下面的数值代表该样本对应的数值区间，优先级高的叶子节点对应的数值区间大，在均匀采样的过程中被选中的概率就高。SumTree的算法实现如算法1所示。

图2 SumTree示意Fig.2 Schematic diagram of SumTree

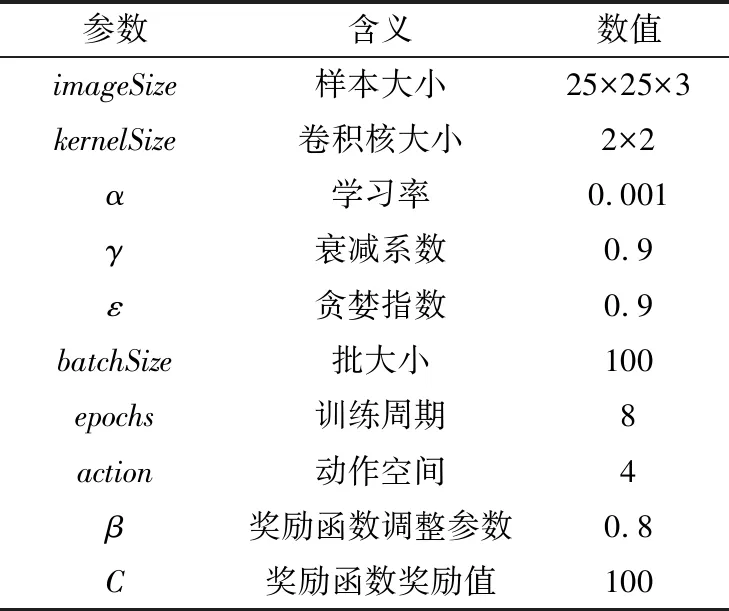
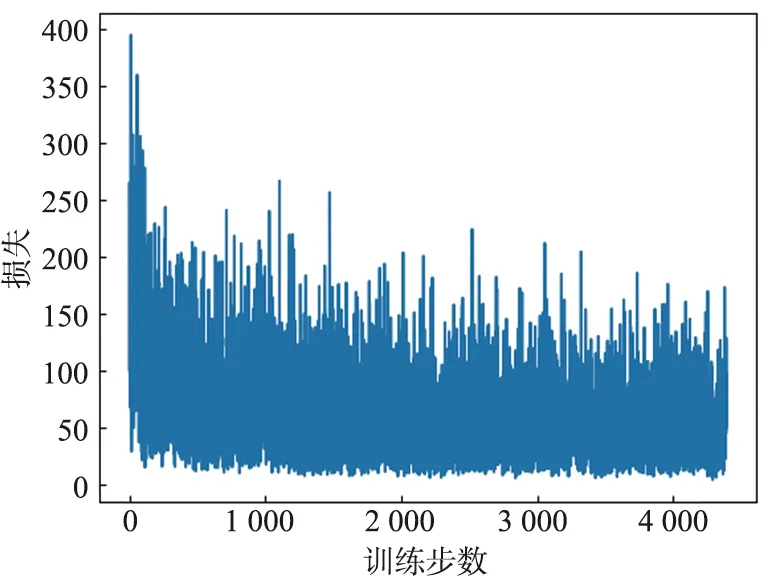
算法1:SumTree算法1) Def SumTree(节点)2) if节点==叶子节点3) ifPriority节点

以图2为例，假如从(0,52)中抽取样本S=25，则从SumTree的根节点0开始，由于左子节点1的优先级为22，小于25，所以选择右子节点2，同时S=25-22=3，然后判断节点2的左子节点5的优先级值是否大于3，依次判断下去，最后选择节点12。

1.3.2 奖励函数的设计

在RL过程中，智能体在与环境的交互中能够获得奖励，驱使智能体在不断的尝试中选择获得奖励多的行为策略。传统的DQN算法奖励函数的设置如下：

(8)

式中，C通常为正整数。可以看出，除去到达目的地和发生碰撞外，其他情况下智能体获得的奖励都是0，通过大量训练虽然能够使智能体到达目的地，但是无法获取最优路线。为此，本文重新设计奖励函数，在没有到达目的地或发生碰撞时，判断下一个行动到达的点中哪一个距离终点距离更近，距离最近的点对应的行动奖励设为βC：

(9)

式中，与目的地的距离通过欧式距离公式计算得出，即:

(10)

式中，x(x1,x2,…,xn)是当前位置坐标；y(y1,y2,…,yn)是目的地坐标。

1.3.3 算法描述

本文提出的PRDQN算法流程如下。

算法2:PRDQN算法1) 生成训练数据集2) 初始化设置,利用CNN生成训练网络(TrainingNet)和目标网络(TargetNet)3) 生成初始Q-table4) 训练网络5) 设置epochs,batchsize等相关变量6) while count

2 实验及结果分析

为了验证算法的有效性，本文设计了如下实验。随机生成200张25 pixel×25 pixel的图片作为NPC行进训练地图，每张图根据不同的起点，再生成25×25=625张图片，共计125 000张，图中随机生成若干黑色像素点代表地图中的障碍。NPC从左上角的像素点[0,0]出发，到达右下角的像素点[24,24]则完成路线规划，中途碰到障碍则失败。实验软件环境：python 3.8,tensorflow 2.4.0,pycharm 2020.3.2。

本文设计了2层卷积网络加2层全连接网络的结构，卷积核大小为2*2，由于图像包含3个通道，因此卷积核的厚度为3，第1次卷积包含10个卷积核，第2次卷积包含20个卷积核，第1层全连接层包含100个神经元，第2层全连接层包含2个神经元，生成的网络结构如图3所示。

图3 算法中深度卷积网络的处理过程Fig.3 Processing flow of deep convolution network in the algorithm

实验程序参数设置如表1所示。

表1 参数设置表Tab.1 Parameter setting

训练过程中的参数变化如图4所示。横轴代表w值，纵轴代表的是分布数量，每个切片代表在当前训练步数下w值的分布情况。

使用同样的训练集，分别对传统DQN算法和PRDQN算法进行训练，损失函数的变化情况如图5所示。

从图5的实验结果可以看出，本文提出的PRDQN算法在收敛性上要好于传统DQN算法，在训练步数到达1 000时，就可以将损失函数值稳定地控制在30以下。

训练完成之后，随机生成10张测试用图，对传统DQN算法和PRDQN算法进行测试，结果如图6所示。

从图6的实验结果可以看出，PRDQN算法生成的规划路线基本沿图像对角线方向，从行进的角度来说，利于NPC在最短的时间内到达指定地点，不仅实现了路线规划，而且优化了行进路线。传统DQN算法虽然也能够完成路线规划，但是路线明显比较曲折。

(a) 第1卷积层的w值

(a) 传统DQN算法

(a) 传统DQN算法的测试效果

3 结束语

本文改进了传统DQN算法的经验回放机制和奖励函数，设计了PRDQN算法。该算法基于TD-error为经验回放单元中的样本设置优先级，并利用SumTree算法实现了优先级经验回放机制。同时，根据NPC行进的需求，重新设计了奖励函数。实验证明，PRDQN算法在收敛性和最优路线规划方面都优于传统的DQN算法。

目前,算法应用于二维地图中，动作空间限于二维空间。在三维仿真训练系统中，行为策略将在三维空间中展开，需要针对奖励函数做进一步改进，考虑地形起伏等更多维度的因素对NPC行进的影响。