基于高阶滑模的自适应Super-Twisting控制系统设计

张旭中，翟道远

(中国科学院湖州应用技术研究与产业化中心，浙江 湖州 313000)

0 引言

滑模控制是一种非线性反馈控制方法，该种方法的鲁棒性较强，在理想状态下，控制系统中的控制器可在一定时间内切换控制信号，将其从一种状态切换到另一种状态，然而在切换过程中，控制器很容易出现抖动情况，导致系统中其他硬件损坏，使系统处于不稳定状态。为了减弱抖振情况，并确保系统具有较强的鲁棒性，国内的专家学者们展开了相关的研究[1-2]。

有学者利用二阶滑模算法设计了自适应Super-Twisting控制系统，该系统利用二阶滑模算法提取了导数的边界值，根据导数边界值的范围识别出控制系统需要的控制参数，通过该参数实现自适应Super-Twisting的控制，该系统的鲁棒性较好，但在应用过程中，控制参数的精度很难保证，从而使控制系统的动态性能较差[3]。

还有学者提出了基于二次型Lyapunov函数的自适应Super-Twisting控制系统，该系统利用二次型Lyapunov函数建立了Super-Twisting控制模型，在模型受常值干扰的条件下，对Super-Twisting进行收敛分析，通过对控制模型优化计算出Super-Twisting收敛的时间，该系统在实现过程中由于缺少硬件设备极易受到不确定干扰，从而导致导数边界未知，对系统中存在的抖振情况不能有效削弱，对Super-Twisting的控制效果较差[4]。

本文为了加强对抖振情况的削弱，设计了基于高阶滑模的自适应Super-Twisting控制系统。分析了高阶滑模控制理论的工作原理，将这一技术应用到控制模块中，通过引入常规线性控制方式和自适应控制方法，优化系统的控制模块，在确定输入信号和输出信号的具体形式后，完成Super-Twisting控制，以两轮自平衡车为研究对象，进行实验仿真，验证控制系统的有效性。

1 自适应Super-Twisting控制系统硬件设计

1.1 采集模块设计

采集模块的核心设备为三星公司生产的AD8036采集器，该款采集器的采样频率较高，最高可达到120 MHz，额定采样速率为80 bit/s，控制信号经过A/D模数转换后，该款采集器的采样速率能提高到140 bit/s，Super-Twisting在经过滑模控制后，其控制参数由于导数边界未知，控制参数的大小会受到控制信号的影响而降低，为此采集模块需要先对控制信号进行调理，调理完成后再采集Super-Twisting的控制参数[5-6]。采集模块结构如图1所示。

图1 采集模块结构

观察图1可知，利用DM9000芯片连接RJ45实现信号的调理。利用TD公司生产的TD6372实现对控制信号的调理，将控制信号控制在ADC转换的电流范围内，TD6372是一种放大器，可以快速且准确地进行脉冲响应，具有较高的分辨率，可作为ADC的缓冲器，ADC为双通道模数转换器，性能好、功耗低，利用TD6372放大器对控制信号调理时，先通过ADC进行模数转换，转换完成后，对控制信号进行偏移匹配，完成后即完成控制信号的调理，再由采集器在导数边界未知的情况下，采集Super-Twisting的控制参数[7-8]。

1.2 存储模块设计

采集模块采集完成Super-Twisting控制参数数据后，这时如果控制系统不能及时接收该控制参数数据，导数边界数据会立刻更新而取代控制参数数据，导致控制参数数据丢失，为此必须对采集完成的控制参数数据进行高速存储[9]。存储模块结构如图2所示。

图2 存储模块结构

观察图2可知，存储模块的核心设备为TD公司生产的TDB7659存储器，该存储器存储容量较大，一次可存储256 kB的数据，缓存速率能达到128 Mbit/s，在存储器存储控制参数数据时，地址发生器能按顺序地进行输入和输出参数，并能按不同的速度读写参数数据。存储模块内部设置了FIFO器件，该器件为SN74ACT7804，具有较高的存储速度，最高可达50 MHz，在访问控制参数数据时时间可缩短为15 ns，该FIFO器件可协助存储器缓存参数数据[10-12]。

存储模块的工作原理为：控制参数数据经过USB接口传输到存储模块后，经过电路传输到FIFO器件上，经过FIFO的缓存后，再通过存储器进行数据写入与读写，同时由存储器进行永久存储。

1.3 控制模块设计

通过高阶滑模实现控制，不仅能够保留传统滑膜控制的优点，提高控制精度，同时也可以防止出现抖动。控制模块引入了滑模控制器。滑模控制采用的非线性控制方法具有很强的鲁棒性，通过采集器获得被控制的对象和参数。选取的滑模动态不会受到对象动态特征参数和扰动影响，因此滑模能够在短时间内实现快速响应，完成参数变化的在线识别。

为了更好地消除滑模控制，利用饱和函数完成边界层的动态控制，在边界层中加入了正常的滑模控制，通过将边界层连续控制完成信息反馈，在反复调整边界层厚度后，缩小厚度，加强控制效果。

微控制器是控制模块的核心设备，该款控制器是由TI公司生产的功耗低、性能好的MSC1210控制器，其时钟频率最高可达40 MHz，单周期指令执行速度为6 m/s，其执行速度是8 051的三倍，同时，该款微控制器设有闪存存储器，存储容量为16 kB，在电压较低时，可进行串行或并行编程，能够进行低压检测，此外，存储模块具有若干个端口，包括：SPI端口、SDI端口、UART端口、USB端口等。控制模块端口结构如图3所示。

图3 控制模块端口结构图

D/A转换器选用三星公司生产的DAC8531，该款转换器功耗较低、单路，属于16位缓冲电压输出，D/A转换器的时钟转换频率最高为45 MHz，电压工作范围为2.5～8.5 V，通过 D/A转换器，将单片机输出的控制参数中的数字量转化成模拟信号，进入信号输入通道。信号输入通道为16路，可反映控制系统的电源状态、负载状态、电压状态、电流状态等，信号输入通道后，可对其进行信号调理，调理结束后由信号输出通道输出，信号输出通道可启动复位信号、极性信号等[13]。

通过常规线性控制方式完成滑模分析，加强控制量增益来消除外界所带来的干扰。本文在控制模块中加入了观测器，通过观测器分析外界的不确定干扰，实现信息控制，从而消除存在的抖振。观测器能够对外界的扰动状态进行估计，根据估计结果得出合适的优化策略，根据系统状态量的考虑结果，直接分析被控制对象的负载力，实现扰动分析。

为更好地完成信息控制，本文在控制模块中引入了自适应方法，在控制过程中，增益不再设定为常数，能够根据系统的运行状态完成随时调整，即使系统没有达到滑动模态时，也能够增加增益，从而完成快速收敛，实现控制工作。

1.4 电路模块设计

电源模块的电压芯片为SW1600，该芯片的核心电压为8.0 V，幅值较低，额定电流为4.2 A，要求具有较好的散热功能。电源模块电路图如图4所示。

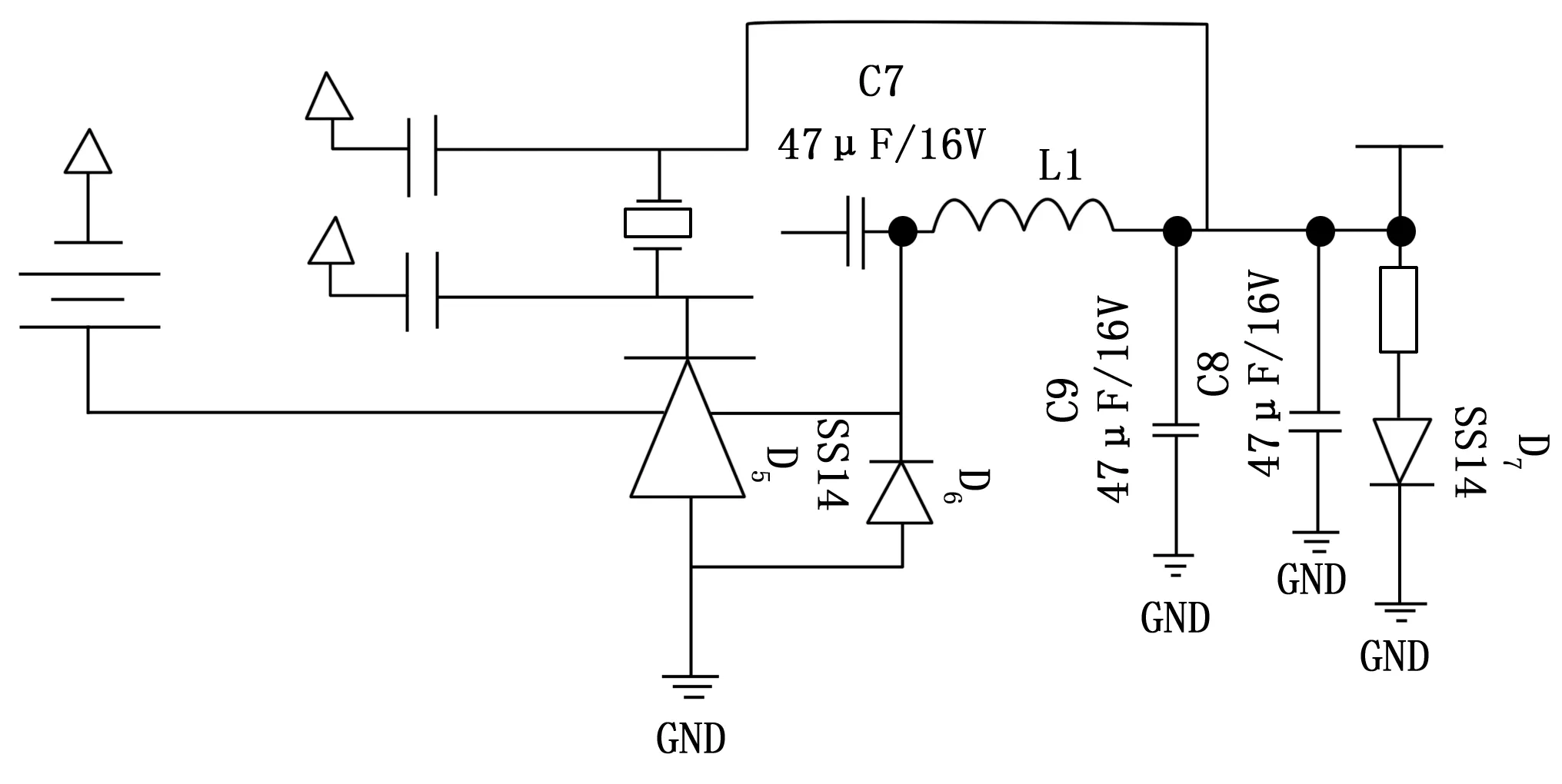
图4 电源模块电路图

电源模块的输出电流为3.2 A，电压波动范围为1.2～8.1 V，系统中如果采集模块、存储模块、控制模块同时进行工作，所需要的电压由电源模块按需进行分配，电源模块中主供供电电压为13 V，当对各个模块分配所需电压时，电源模块选择集成电源模块，该模块电流大，输入与输出压差可提高电压的转换效率，根据各个模块的电压需求，对各个模块的核心电压进行上电控制[14]。

2 自适应Super-Twisting控制系统软件设计

在完成硬件设计后，引入高阶滑模理论设计软件程序。滑模控制为一种非线性控制方法，其结构较为简单，对参数及各类不确定干扰因素都不敏感，具有较好的鲁棒性，广泛应用于各种控制系统中[15-17]。本文采用高阶滑模，主要通过该种算法设计Super-Twisting控制器，以实现Super-Twisting的自适应控制。

基于高阶滑模的自适应Super-Twisting控制系统软件流程如图5所示。

图5 基于高阶滑模的自适应Super-Twisting控制系统软件流程

首先，由主程序完成系统的初始化。系统中的主程序主要负责对控制系统中的硬件电路进行初始化，消除时钟的延时，合成频率，并调整时钟相位，同步到控制芯片上，以此实现控制芯片内、外时钟控制的一体化。在初始化过程中，ADC将采集器提供的80 MHz时钟信号合成为16 MHz、75 MHz的时钟并进行逻辑处理，控制程序对参数数据的读写速度可调整到30 bit/s，通过输出通道进行输出[18]。采集信号通过虚拟控制定律可以得到，采集过程得到的信号能够实现反步迭代控制，信号输出模式为非线性模式，满足虚拟控制规律。采集信号与输出信号的模式如图6所示。

图6 采集信号与输出信号模式

根据图6可知，数据的个数在不断增加，最后达到50×104，数据数值的波动定点最高能够达到4 800，波动时间间隔为10×104，采集端信号与输出端信号存在较大的差异，采集端的信号模式为不规则模式，呈现明显的不规则波动，而输出端信号能够保证信号与标准方式运行。

然后，设计Super-Twisting 控制器。Super-Twisting滑模控制是在高阶滑模理论下实现，属于2-滑动控制器，将采集程序采集的控制参数数据转换为系统的控制量，将该控制量应用到导数中，通过下式进行表示：

(1)

式中，u表示由采集程序采集的参数控制量；x表示Super-Twisting滑模控制的收敛量；y表示输入状态量；a，b，c分别表示增益函数、未知函数与滑动变量函数；t表示动态量。

本文研究的Super-Twisting控制系统阶数设定为1，这样能够确保系统在运行过程中的连续性，防止出现滑模控制的抖振问题，分析Super-Twisting在公式(1)中的变量函数的平滑变量方式，与传统的Twisting算法相比，Super-Twisting能够在短时间内实现滑模变量收敛，从而消除抖振问题。

通过滑动阶完成连续求导，分析运动动态的平滑度，确定约束条件，完成精准定义，在轨迹状态的交界处确定二阶滑模的动态形式，增加系统的鲁棒性，防止系统出现抖动。在SOS相平面上，设置有效的原点，确保系统是否能够围绕原点轨迹完成旋转，在有限的时间内，实现环绕收敛，在多次收敛中，确保系统能够恢复到原点。

Super-Twisting能够利用切换装置完成信息切换，实现理想的切换，在控制过程中，设定控制量能够通过正常的方式显示在S中，使滑模面在工作过程中不会受到限制。

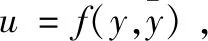
(2)

式中，u1表示控制系统中的反馈控制量；K表示特定增益；sgn(y)为符号函数。

利用二阶滑模控制来消除系统运行过程的抖振，使系统能够维持二阶滑动状态，在有限的时间内完成信息收敛，系统运行过程中会存在多次收敛，因此能够实现分析。

最后，进行自适应控制。该Twisting控制器不需要设置变量导数，只要保证在进行自适应控制与收敛时，滑动面的稳定性处于标准范围即可[20-21]。当特定增益K增大到足够大时，可形成STSM控制器，该控制器是一个指数较为稳定的控制器，可协助Super-Twisting进行自适应控制，本文设计的自适应Super-Twisting滑模控制律ui如下：

(3)

式中，l表示状态估计变量；b0表示切换增益；-uj表示抖振变量；-uj表示常数[22-23]。

根据上述过程实现Super-Twisting控制，完成信息分析，通过高阶滑模控制改变信息在控制过程中存在缺陷定点改善，提高系统的运行能力[24-25]。

3 实验研究

为了验证本文设计的基于高阶滑模的自适应Super-Twisting控制系统的有效性，选用本文设计的系统与传统的基于二阶滑模算法的自适应Super-Twisting控制系统、基于二次型Lyapunov函数的自适应Super-Twisting控制系统进行实验对比。

本文选用的控制对象为两轮自平衡车，作为一种欠驱动系统，两轮自平衡车以一种非线性模式运行，能够完成不稳定工作，因此使用这种方法验证系统的实际应用效果。

为验证本文所设计的基于高阶滑动模态的自适应Super-Twisting控制系统的有效性，选取了基于二阶 Lyapunov的自适应滑动模态控制器。试验对比Super-Twisting控制系统的性能。

选用的实验仿真参数如表1所示。

表1 实验仿真参数

根据上述参数，进行仿真对比实验。

选用本文控制系统和传统控制系统进行对比实验，分别对信号的电流、位置和速度进行控制，得到的控制响应时间实验结果如表2所示。

表2 控制响应时间

根据表2可知，在10次实验中，3种系统的响应时间不同，本文所讨论的基于高阶滑模的自适应Super-Twisting控制系统的响应时间均不超过0.1 s，具有很好的控制效果，而基于高阶滑模的自适应Super-Twisting控制系统，其响应时间为2～3 s，以二阶李雅普诺夫函数为基础，其响应时间为3～4 s。由此可见，本文提出的控制系统控制能力更强，能够在短时间内实现响应，具备实时响应能力。

在确定控制响应时间后，对控制精度进行分析，同时使用基于高阶滑动模态的自适应Super-Twisting控制系统、基于二次型Lyapunov函数的自适应Super-Twisting控制系统和基于二阶 Lyapunov的自适应滑动模态控制器，对两轮自平衡车进行平衡控制，并通过仿真对比，完成实验，记录电流控制精度、位置控制精度和速度控制精度。

分析图7可知，标准电流波动范围在-42～42 A之间，基于二阶滑模算法的自适应Super-Twisting控制系统的电流波动范围在-24～24 A之间，基于二次型Lyapunov函数的自适应Super-Twisting控制系统波动范围在-36～36 A之间，本文提出的基于高阶滑模的自适应Super-Twisting控制系统电流波动范围在-40～40 A之间。由此可见，本文提出的控制系统控制时间与标准值最为接近，控制能力最好。

图7 电流控制结果

分析图8可知，随着时间的增加，控制角度也会逐渐增大，而基于二阶滑模算法的自适应Super-Twisting控制系统的偏离角度最大，当控制时间为5 s时，偏离角度为0.8°，基于二次型Lyapunov函数的自适应Super-Twisting控制系统的偏离角度为0.65°，本文提出的基于高阶滑模的自适应Super-Twisting控制系统的偏离角度仅为0.1°，能够保证系统正常运行。

图8 位置控制结果

分析图9可知，在10～15 s之间速度出现一个峰值，要想对其进行控制，确保控制效果与标准值相符合较为困难。文中采用了基于高阶滑动模态的自适应Super-Twisting控制系统，在5 rpm范围内实现。在此基础上，基于二阶滑模算法的自适应Super-Twisting控制系统明显低于标准，接近25 rpm。第二级 Lyapunov功能自适应Super-Twisting控制系统的标定大于10 rpm。

图9 速度控制结果

综上所述，基于高阶滑动模态的自适应Super-Twisting控制系统、基于二次型Lyapunov函数的自适应Super-Twisting控制系统和基于二阶 Lyapunov的自适应滑动模态控制器都能够使自适应平衡车达到平衡状态，可是在性能上却存在明显差异，本文提出的系统与传统滑模方式相比，控制的精度明显提高，系统的整体响应能力更强，能够在短时间内调整状态，完成响应。3种系统的控制性能如表3所示。

表3 系统控制能力实验结果

根据表3可知，在使用3种滑模控制系统后，两轮自平衡车显现出不同的性能。使用基于二次型Lyapunov函数的自适应Super-Twisting控制系统后，平衡车仍然存在抖振，即使系统步入稳态后，这种抖振现象都没有得以缩减，而基于二阶 Lyapunov的自适应滑动模态控制器在减小抖振方面明显优于基于二次型Lyapunov函数的自适应Super-Twisting控制系统，但是系统所选取的参数采用试凑法选择，受到的制约因素较多，尤其是在存在干扰状态下，控制性能较弱。本文提出的控制系统在不受外界干扰影响，利用高阶滑模完成控制，使两轮自平衡车在运行过程中抖振现象得以明显减小。

本文提出的系统整体控制能力较强，在无法确定是否存在干扰下，仍然能够获得动态性能，从而展示系统较好的鲁棒性，在实际应用工程中具有很好的适用性。

4 结束语

为了解决传统控制系统出现的问题，本文设计了基于高阶滑模的自适应Super-Twisting控制系统，在运用高阶滑模理论的情况下，实现了Super-Twisting的自适应控制，系统具有较好的鲁棒性与应用效果，可以削弱系统中存在的抖振。本文引入了高阶滑模理论，在确定滑模控制原理后，完善控制模块，使控制模块能够当作微分器使用，提高系统的鲁棒性。在仿真实验中，本文设计的系统展示出优异的控制性能，对于之后研究观测器，提供了重要的理论基础。但是本文系统在应用过程中忽视了采样周期对于控制性能的影响，缺少对信号频率的考虑，为了利用微分器提高滑块速度，而忽略了噪声影响，牺牲了积分消除运算，容易出现不稳定。

由此可见，本文系统还需要更多的完善，在下次的研究中，将重点对使用Super-Twisting的稳定性进行分析，根据扰动理论和控制理论将扰动观测器与控制器结合，防止外界干扰降低系统的鲁棒性，引入自适应思想来提高系统的观测能力，增强鲁棒性。